En optimeringsopgave - LMFK

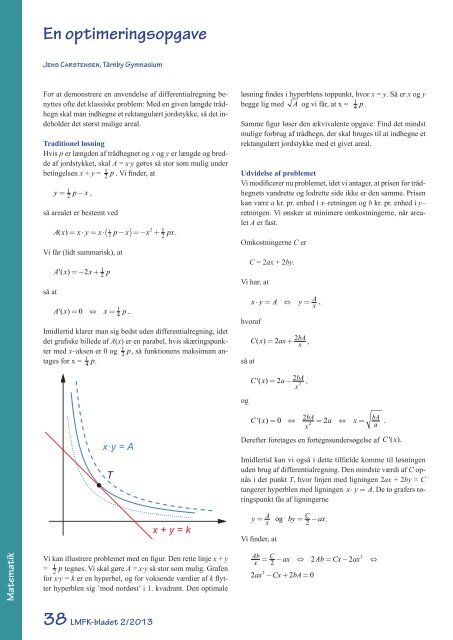
En optimeringsopgaveJens Carstensen, Tårnby GymnasiumFor at demonstrere en anvendelse af differentialregning benyttesofte det klassiske problem: Med en given længde trådhegnskal man indhegne et rektangulært jordstykke, så det indeholderdet størst mulige areal.Traditionel løsningHvis p er længden af trådhegnet og x og y er længde og breddeaf jordstykket, skal A = x·y gøres så stor som mulig underbetingelsen x + y = 1 2p . Vi finder, aty =12p−x ,så arealet er bestemt ved( ) = − +1A( x) = x⋅ y = x⋅ p−x x pxVi får (lidt summarisk), atså atA'( x) = − 2x +12pA'( x) = 0 ⇔ x =14p.22 12.løsning findes i hyperblens toppunkt, hvor x = y. Så er x og ybegge lig med A og vi får, at x =14p .Samme figur løser den ækvivalente opgave: Find det mindstmulige forbrug af trådhegn, der skal bruges til at indhegne etrektangulært jordstykke med et givet areal.Udvidelse af problemetVi modificerer nu problemet, idet vi antager, at prisen for trådhegnetsvandrette og lodrette side ikke er den samme. Prisenkan være a kr. pr. enhed i x–retningen og b kr. pr. enhed i y–retningen. Vi ønsker at minimere omkostningerne, når arealetA er fast.Omkostningerne C erC = 2ax + 2by.Vi har, atx⋅ y = A ⇔ y =Ax,hvorafså atC( x) = 2ax+2bAx,Imidlertid klarer man sig bedst uden differentialregning, idetdet grafiske billede af A(x) er en parabel, hvis skæringspunktermed x–aksen er 0 og 1 2p, så funktionens maksimum antagesfor x = 1 4 p. x·y = AogC '( x) = 2a−2bAx2,C '( x) = 0 ⇔2bA= 2a ⇔ x =xbAa2.Derefter foretages en fortegnsundersøgelse af C '( x).TImidlertid kan vi også i dette tilfælde komme til løsningenuden brug af differentialregning. Den mindste værdi af C opnåsi det punkt T, hvor linjen med ligningen 2ax + 2by = Ctangerer hyperblen med ligningen x⋅ y = A. De to grafers røringspunktfås af ligningernex + y = ky = A og by =C−axx2..Vi finder, atMatematikVi kan illustrere problemet med en figur. Den rette linje x + y= 1 2p tegnes. Vi skal gøre A = x·y så stor som mulig. Grafenfor x·y = k er en hyperbel, og for voksende værdier af k flytterhyperblen sig ’mod nordøst’ i 1. kvadrant. Den optimaleAb Cxax Ab Cx ax2= − ⇔ 2 = −2⇔222ax − Cx + 2bA= 038 LMFK-bladet 2/2013

x =C abA bAa=16=4 4 a a .x·y = ADerefter får viy =A A aAx= = b.bAaTHvis på den anden side omkostningerne C til trådhegnet er faste,opnås det største areal forx =C, y =C,4a4 bog dette giver AC16 ab.= 22ax + 2by = CDa hyperblen og linjen har netop et punkt fælles, er diskriminanten0, dvs.Man kan se på andre tilfælde end ovenfor nævnte, idet man kanantage, at den ene side af grundstykket vender op til en mur,hvor der ikke skal bruges trådhegn. I så fald er y + 2x = C. Enanden mulighed er at gå ud fra, at den ene side af grundstykketfår udgifterne delt med naboen, så C = 2y + 3 2 x.2C −4⋅2a ⋅ 2bA = 0 ⇔2C = 16abA,og roden i ligningen erHenvisningMarcus Bizony Bishops: Fencing a Field, Mathematical Digest,October 2012, University of Cape Town.LMFK-bladet 2/2013 39Matematik