Psychologische Diagnostik - Universität Regensburg

Psychologische Diagnostik
True score Theorie
WS 2010/11
Prof. Dr. Jan Drösler
Universität Regensburg
Einführung
Wissenschaftliche Durchdringung der
Psychodiagnostik ist erforderlich, weil
intuitive Anwendung von „Menschenkenntnis“
im wesentlichen zu Selbsttäuschung
führt. Die Erfahrung zeigt, daß freihändige
Verfahren der psychologischen Diagnostik,
etwa Untersuchungsgespräche aus
dem Stegreif, in der Regel von verschwindender
Gültigkeit sind.
Ein verbreiteter Fehler der Psychodiagnostik
besteht darin, den Unterschied von
Testergebnis und dessen Bedeutung zu
übersehen. Beispiel: Testergebnis ist „kann
[Oachkoatzlschwoaf] korrekt aussprechen“,
Bedeutung : „ist ein Eingeborener“
bzw. „kein solcher“ Zuordnung von Ergebnis
(Befund, U) zu Bedeutung, (Kriterium
, Θ )m allgemeinen nur stochastisch
als p(Θ | U).
Rückgriff auf mehrere Befunde.
Das Grundproblem der Psychodiagnostik
ist überraschenderweise die Auswertung
der Ergebnisse von Mehrfachzugriffen,
also die Auswertung eines „Tests“. Ist es
vertretbar, „Testpunkte“ zu addieren und
Die so entstandenen Summen zu interpretieren?
Beispiel: vier Zugriffe („Items“):
Nur naive Personen, wie solche, die sogenanntes
„Ranking“ betreiben, halten hier
nur fünf verschiedene Antwortmuster für
möglich. In Wirklichkeit sind es 16, allgemein
zwei hoch die Anzahl der Aufgaben.
Das wissenschaftliche Problem der psychologischen
Diagnostik besteht darin,
nachzuweisen, dass Versuchspersonen mit
der gleichen Anzahl korrekter Lösungen
psychologisch äquivalent sind.
Verschiedene Zugänge
1 Meßtheoretisch : Formuliere die Voraussetzungen
in empirischer Sprache und
prüfe sie.
2 Statistisch a: Sorge für die Erschöpfungseigenschaft
der erwünschten Summenstatistik,
oder b: Zeige empirisch die

(stochastische) Abhängigkeit der Testskala
von der Kriteriumsskala.
Als Gültigkeit oder Validität wird die Bedeutung
eines Untersuchungsergebnisses
über sich selbst hinaus bezeichnet. Zur
Erreichung einer wissenschaftliche Nachprüfbarkeit
von Untersuchungsergebnissen
ist Objektivität der Untersuchung geboten.
Das Verfahren muß so organisiert sein, daß
die Ergebnisse nicht von der Person des
Untersuchers abhängen.
Dennoch lässt sich die gewünschte Reproduzierbarkeit
der Ergebnisse nicht erreichen.
Wiederholungen einer Untersuchung
am gleichen Probanden fallen unterschiedlich
aus. Sie sind im einzelnen nicht vorhersagbar.
Die Psychologie ist zu der Feststellung
veranlasst, das menschliches Verhalten,
sowohl das Antwortverhalten in
einem Test, wie auch das Verhalten in Bezug
auf das die Bedeutung des Tests tragenden
Kriteriums zufällig ist. Verhalten
ist nicht im einzelnen, sondern nur als Angabe
einer Menge von möglichen Ergebnissen
vorhersagbar.
Testverfahren
Ein Quintupel < Ω, , , f, X > ist ein
Testverfahren, wenn Ω eine Menge von
Elementarantworten zu einer Aufgabensammlung,
eine σ-Algebra von Teilmengen
aus Ω ist, ein Wahrscheinlichkeitsmaß
auf , f : Ω → Φ
eine Abbildung in die Menge Φ der untersuchten
Personen und X : Ω → eine Zufallsgröße
ist, z.B. die Summe der richtigen
Lösungen.
Beispiel (Thurstone, 1943). Instruktion:„Markiere
den Bereich, der von einer
gestrichelten und einer durchgezogenen
Figur eingeschlossen ist“.
Ein Beispiel eines Antwortmusters für
einen Test, der aus nur einer Aufgabe besteht,
ist die Menge Ω = {„richtig“,
„falsch“}. Bei einem Test mit mehreren
Aufgaben besteht diese Ereignismenge
meist aus der Menge der durchnumerierten
Antwortmöglichkeiten bzw. der Menge
der namentlich gekennzeichnete durchnumerierten
Antwortprotokolle.
Aufgabe der psychologischen Diagnostik
ist es, den mit einem bestimmten Ergebnis
oder einer logischen Kombination von
mehreren Ergebnissen verbundenen Grad
an Gewißheit z. B. einer korrekten Lösung
für eine Person zu bestimmen.
Der naturwissenschaftliche Wahrheitsbegriff
wird auch in der psychologischen
Diagnostik eingesetzt. Diagnosen sind nur
dann wahr, wenn sie als Prognosen verstanden
werden können und tatsächlich
eintreffen. Der Grad, mit dem das empirisch
der Fall ist, heißt Validität. Um den
Begriff der Validität begründen zu können,
sind einige Voraussetzungen zu klären.
Skalierung der Gewissheit nach Kolmogorov
(1933).
Sei Ω eine Menge von Ergebnissen. Alle
logischen Kombinationen der Elemente
von Ω sollen verfügbar sein. Das geschieht
mittels einer
σ-Algebra von Teilmengen von Ω . Sie
ist bezüglich dem Mengendurchschnitt
und der Mengenvereinigung auch gegenüber
abzählbarer und abzählbar unendlicher
Anwendung abgeschlossen. Letztere
Vereinbarung ist für die Behandlung von
Mengenfolgen erforderlich, die in den
Anwendungen der Wahrscheinlichkeitstheorie
vorkommen.
Damit ist die Verfügbarkeit der denkbaren
logischen Kombinationen von Elementen
aus Ω gegeben. Weil eine solche Mengen-

algebra umkehrbar eindeutig auf die Aussagenlogik
abbildbar ist, lassen sich die
Verknüpfungen und auch als „und“
bzw. „oder“ lesen. Besteht also die Ergebnismenge
Ω aus den Antwortmustern, dann
lässt sich aus die Menge der Protokolle
herausgreifen, die beispielsweise die dritte
und die fünfte Aufgabe als richtig beantwortet
ausweisen.
Ein Paar < Ω, > heißt meßbarer Raum.
Auf ihm ist ein Maß μ einführbar, das die
Eigenschaften besitzt, die uns beispielsweise
von der Flächenmessung her geläufig
sind: Ein Maß ist eine gegenüber disjunkten
Elementen additive,
(A B) = (A) + (B) gdw. A B =,
nichtnegative Abbildung nach ,
(A) 0 für alle A , mit μ( ) = 0.
Wahrscheinlichkeit als spezielles Maß der
Gewissheit. Die Wahrscheinlichkeit ist
ein auf μ( Ω) = 1 normiertes Maß auf dem
messbaren Raum < Ω, >. Das Tripel <
Ω, , > bildet einen Wahrscheinlichkeitsraum.
Seine Einführung im Zusammenhang der
Testtheorie ermöglicht die wissenschaftliche
Analyse des zufälligen Antwortverhalten
der untersuchten Personen und
deren Testergebnisse als Zufallsgrößen.
Zufallsgrößen sind Abbildungen der
Grundmenge Ω eines Wahrscheinlichkeitsraumes
< Ω, , > in die reellen Zahlen
, so daß die Umkehrabbildung existiert
und ihre Bilder in liegen. Beispiele sind
alle zahlenmäßigen Testauswertungen,
etwa die Rohwerte, die Versuchspersonen
an einem Intelligenztest erzielt haben. In
diesem Falle besteht Ω wieder aus der
Menge aller möglichen Antwortmuster des
Tests. Die Meßbarkeit beispielsweise der
Abbildung „Intelligenzquotient“ (IQ) ermöglicht
bei gegebenem IQ mittels Umkehrabbildung
die Bestimmung der Wahrscheinlichkeit
des Auftretens einer Person
mit mindestens diesem IQ .
Schwache Truescore-Theorie
Truescore Theorie ist dadurch gekennzeichnet,
daß sie die Testrohwerte als Befunde
einer diagnostischen Untersuchung
in zwei Komponenten aufspaltet, den sogenannten
wahren Anteil und die Fehlerkomponente.
Schwache Truescore-Theorie
verzichtet dabei auf Annahmen über die
Verteilungen dieser Komponenten oder der
Rohwerte selbst. Sie setzt lediglich die
Existenz niederer Momente dieser Verteilungen
voraus. Unter diesen Momenten
sind vor allem der Erwartungswert, die
Varianz und im zweidimensionalen Falle
die Kovarianz zu nennen.
Der Erwartungswert einer Zufallgröße
X ist definiert als X = X p(X), wobei
das Produkt der Ausprägung der Zufallsgröße
und der entsprechenden Auftretenswahrscheinlichkeit
über den gesamten Bereich
von X zu summieren, (im kontinuierlichen
Falle, z. B. bei Reaktionszeiten, zu
integrieren) ist. Die Erwartungswertbildung
ist ein linearer Operator:
(X + Y) = (X) + (Y)
( X) = (X),
(Additivität),
(Homogenität).
Der Erwartungswert sollte nicht mit dem
(Stichproben-)Mittelwert verwechselt werden.
Dieser ist als Summe der mit den
Häufigkeiten gewichtete Summe der verschiedenen
Realisierungen einer Zufallgröße,
dividiert durch deren Anzahl definiert.
Er dient meist zur Schätzung des
Erwartungswerts. Die Varianz einer Zufallsgröße
X ist definiert als var(X) =
²(X) = X² - (X)².
Die Kovarianz zweier Zufallsgrößen X und
Y ist definiert als cov(X,Y) = XY - X
Y. Validität wird als statistischer Korrelationskoeffizient
zwischen Test und Kriterium
ausgedrückt. Ein Korrelationskoeffizient
xy ist die auf das geometrische Mittel
der Varianzen [²(x)²(y)] normierte
Kovarianz von X und X: xy = cov(X,Y)/
[²(X)²(Y)] Validitätskoeffizienten,
lassen sich wie die Erfahrung gelehrt hat,

von Null für freihändiges Vorgehen mittels
objektiver Tests auf Werte um 0,55 (für
einen zweijährigen Prognosezeitraum) erhöhen.
Testverfahren
Ein Quintupel < Ω, , , f, X > ist ein
Testverfahren, wenn Ω die Ergebnismenge
ist (in der Anwendung meist diejenige
Menge von Aufgabenprotokollen, die die
kleinste Auswertungseinheiten sind),
eine σ-Algebra von Teilmengen aus Ω
ist, ein Wahrscheinlichkeitsmaß auf ,f : Ω → Φ eine zufällige Abbildung
in die Menge Φ der untersuchten Personen,
mit der die Testprotokolle den untersuchten
Personen zugeordnet werden, und X :
Ω → , der Rohwert, eine Zufallsgröße
ist. Die untersuchte Person wird als zufällig
aus der Personenmenge Φ ausgewählt
betrachtet.f : Ω → Φ , ω α Auch hier ist
damit impliziert, daß die Umkehrabbildung
f^(-1) existiert und ihre Bilder in einer σ-
Algebra über Ω liegen. Mittels f^(-1)(α)
= B ist die Teilmenge B aller von einer
bestimmten Person α erzeugten Antwortmuster
.Mittels f wird demnach die
Menge aller Antwortprotokolle Ω in eine
Menge von Äquivalenzklassen Ω/ f =
zerlegt. Jede Äquivalenzklasse enthält alle
Antwortprotokolle einer bestimmten Person
f(ω) Wenn bei Zufallsgrößen, wie es
Testergebnisse sind, Varianzen und Kovarianzen
gegeben sind, so kann man deren
Definition leicht in ein allgemeineres algebraisches
Konzept einbringen, das interessante
Möglichkeiten des Theoretisierens
eröffnet.
Die einfachste Zufallsgröße
Besonders einfache Zufallgrößen kommen
häufig in der Psychologie vor und besitzen
die Ausprägungen Null und Eins. Beispiele
von Ereignismengen, die zu derartigen
Zufallsgrößen führen. {ja, nein}, {stimme
zu, stimme nicht zu}, {männlich weiblich},
{richtig, falsch}, {Kopf, Wappen},
{sechs gewürfelt, andere Augenzahl gewürfelt}.
Da nur zwei Zahlenwerte mit
bestimmten Wahrscheinlichkeiten anfallen
, spricht man von einer Zweipunktverteilung.
Die elementare Beobachtung
Zweipunktverteilungen beschreiben das
Verhalten bei einer gegebenen Alternative.
Man könnte u. a. an „Tests“ denken, die
aus einer einzigen Aufgabe bestehen. Das
wissenschaftliche Problem lautet: Besitzt
die Beobachtung einer bestimmten Alternative
irgendeine Bedeutung über sich
selbst hinaus?
Ergebnis und Bedeutung
Untersucht wird, ob das Ergebnis mit irgend
einer infragekommenden Bedeutung
in Zusammenhang steht. Da von zufälligen
Ereignissen die Rede ist, wird nach einem
Zusammenhang in Wahrscheinlichkeit
gesucht.
Unabhängigkeit zweier Ereignisse A und B
liegt vor, wenn gilt P(A | B) = P(A). Abhängigkeit
ist gegeben, wenn statt dessen
die Ungleichheit gilt.
P(A | B) ≠ P(A).
Empirische Überprüfung
Zur Prüfung der Abhängigkeit eines Ergebnisses
und dessen mutmaßlicher Bedeutung
ist eine empirische Untersuchung
erforderlich. Beispiel: Bedeutet die Verwicklung
in einen Verkehrsunfall, daß die
Person als „unvorsichtig“ zu charakterisieren
ist? Wir beobachten 100 Versuchspersonen
über ein Jahr:
Zusammenhang von Beobachtung
und Bedeutung
Die Ereignisse A und B sind stochastisch
unabhängig, wenn die bedingte Wahrscheinlichkeit
von A gegeben B gleich der
Unbedingten Wahrscheinlichkeit von A ist:

er-
17
(22)
Ziel
reicht
„nicht
gelöst“
Ziel nicht 37
erreicht (32)
„gelöst“
25
(20)
25
(30)
Summe
42
62
Summe 54 50 104
Falsche Entscheidungen
Man vermeidet die Blamage, fälschlich
einen (neuen) Effekt für die Wissenschaft
zu behaupten, wenn man die entsprechende
Irrtumswahrscheinlichkeit „der ersten Art“
möglichst klein ( 0,01 oder 0,05) ansetzt.
Einen bestehenden Effekt zu übersehen gilt
als weniger ehrenrührig. Die entsprechende
Irrtumswahrscheinlichkeit „der zweiten
Art“ wird höher angesetzt (> 0.2).
( A | B ) = ( A ).
Diese Beziehung ist empirisch prüfbar
Kontingenztafel
Die Nullhypothese
Fehlende stochastische Abhängigkeit liegt
vor, wenn die Beobachtungen in allen vier
Feldern proportional zu den Randsummen
auftreten. Genau dann sind nämlich die
bedingten Wahrscheinlichkeitsschätzungen
gleich den unbedingten. Man berechnet
deshalb die unter der Nullhypothese erwarteten
Häufigkeiten durch Multiplikation
der zugehörigen Randsummen und Division
durch die Gesamtsumme
Zufallskritische Prüfung
Die „Nullhypothese“ ist statistisch prüfbar,
sobald man über eine Prüfgröße verfügt.
Für Kontingenztafeln wurde diese von
Pearson entwickelt. Er wies nach, daß die
Summe der quadrierten Differenzen von
beobachteten und erwarteten Häufigkeiten,
bezogen auf die erwarteten Häufigkeiten,
χ²-verteilt mit einem Freiheitsgrad ist. Hier
ergibt sich χ² = 3,6, nicht signifikant. Die
Nullhypothese wird beibehalten
Ansatz der klassischen Testtheorie
Die klassische Testtheorie geht davon aus,
daß zwischen dem Testergebnis und seiner
Bedeutung (dem Kriterium) streng zu unterscheiden
ist. Sie stellt in Rechnung, daß
das Kriterium durch das Testergebnis nicht
sicher, sondern nur in Wahrscheinlichkeit
determiniert ist. Grund dafür sei eine Unschärfe
des Testergebnisses.
Reproduzierbarkeit von Testergebnissen
Der empirische Ansatz zur Bearbeitung
dieses Programms ist die Bestimmung der
Unschärfe des Testergebnisses an Hand
seiner Reproduzierbarkeit (Reliabilität). Zu
diesem Zweck sind psychologische Untersuchungsverfahren
stets mehrfach an den
gleichen Personen anzuwenden. Das erzeugt
offenkundige neue Schwierigkeiten
und verlangt deshalb nach einer Theoretischen
Aufarbeitung.
Alternative Darstellungen
Die Reproduzierbarkeit von Testergebnissen lässt
sich auf verschiedene, grundsätzlich gleichwertige
Weisen darstellen. Damit man Zeichnungen herstellen
kann, werden vorübergehend Verteilungsannahmen
für die Befunde eingeführt. Sie sollen unimodal
und symmetrisch im Sinne der Gaußschen
Normalverteilung auftreten.

f( x )
1
2
2 e
x 2
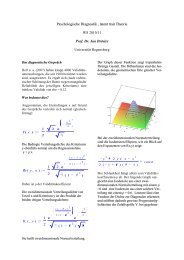
Es ergibt sich für die Testergebnisse die bekannte
glockenförmige Verteilungsdichte:
2
Nun kann man die gemeinsame (zweidimensionale)
Verteilungsdichte zeichen. Graph der gemeinsamen
Dichte für rho = 0,8 :
Isodensiten
Normalverteilte Testergebnisse (Erwartungswert
null, Varianz eins).
Bedingte Verteilungsdichte
Manchmal verzichtet man auf eine perspektivisch
dreidimensionale Darstellung und gibt den Sachverhalt
durch Ellipsen in der x-y Ebene wieder.
Diese „Isodensiten“ hängen mit der zweidimensionalen
Verteilungsdichte so zusammen, wie die
folgende Abbildung zeigt.
Will man den Grad der Reproduzierbarkeit graphisch
darstellen, so bezieht man sich auf eine
zweidimensionale Verteilungsdichte von, beispielsweise
Testdurchführung und einer Testwiederholung
nach zwei Wochen. Um diese zweidimensionale
Dichte zeichen zu können, bedarf es
einer Annahme über die bedingten Verteilungsdichten.
Das sind die Ergebnisse der Wiederholungsuntersuchung,
abgetragen für ein festes Ergebnis in
der ersten Testdurchführung. Hier wird angenommen,
eine brauchbare Wiederholbarkeit liege vor,
dea erste Testergebnis bestimme denMittelwert der
bedingten Verteilungen linear. Man spricht von
einer lineare Regression, E(Y|x) = ρ x. Die bedingte
Varianz sei 1 – ρ².
fb ( y,
x )
Gemeinsame Verteilungsdichte
Multipliziert man die bedingte Dichte fb(x,y) [ sie
wird sonst durch f (y | x) abgekürzt] mit der unbedingte
Dichte f (x), so erhält man die gemeinsame
Dichte f (x,y):
f ( x,
y )
1
2
1
2
e
2 e
( y x )
2
2
2 ( 1 )
1
x 2 2 x y y 2
2
2 ( 1 )
1
2
2
Zweidimensionales Streuungsdiagramm
Schließlich ist auch eine graphische Darstellung
von zweidimensionalen Stichproben üblich. Jede
Versuchsperson ist durch zwei Werte charakterisiert,
ihren Wert in der ersten Untersuchung und
ihren Wiederholungswert. Benutzt man diese beiden
Werte als x- und y-Wert in einem Koordinatensystem,
so entsteht ein Streuungsdiagramm:

definiert ist, für die weiterhin eine assoziative
Verknüpfung . , die skalare Multiplikation
mit Zahlen definiert ist, heißt
Raum, seine Elemente Vektoren.
Zweck der formalen Testtheorie
Ziel einer formalisierten Testtheorie ist es, beweisbare
Aussagen über die Reproduzierbarkeit (Reliabilität)
und die diagnostische Bedeutung (Validität)
der Befunde (Testergebnisse) zu tätigen. Das
bezieht sich z. B. auf die Abhängigkeit dieser Gegebenheiten
von der Länge des Tests oder auf deren
Zusammenhang untereinander.
Traditionelle Theorie
Bis in die siebziger Jahre galt es als erforderlich,
detaillierte Annahmen über die
Ursache der Unschärfe der Befunde und
ihren stochastischen Zusammenhang mit
anderen Größen, z. B. dem reproduzierten
Befund aufzustellen (Gulliksen, 1950).
Nach heutiger Sicht ist die bei geeigneter
Wahl eines theoretischen Ansatzes überflüssig
(Zimmermann, 1975).
Ist außerdem ein Skalarprodukt für alle
Paare a, b das Skalarprodukt als < a, b > =
a1b1 + a2b2 + ... + anbn definiert, so läßt sich
eine Norm durch |x| = < x, x > ^(1/2) einführen.
Gilt für diese Norm, daß sie nichtnegativ
ist, den Wert Null nur für x = 0
annimmt, Homogenität bei der Multiplikation
mit Zahlen und die Dreiecksungleichung
gelten, so spricht man von einem
euklidischen Raum.
Ein Beispiel für einen dreidimensionalen
( n = 3 ) euklidischen Raum ist der physikalische
Raum (im Kleinen) um uns. Er
besitzt die wichtige Eigenschaft der Zerlegbarkeit
in orthogonale Unterräume.
Zwei Unterräume sind orthogonal zueinander,
wenn das Skalarprodukt je eines
Vektors aus einem mit einem Vektor aus
dem anderen Unterraum verschwindet.
Geometrisch läßt sich Orthogonalität von
Vektoren als Rechtwinkligkeit repräsentieren.
Durch einen geeigneten Operator : V
V läßt sich ein Vektor des Raumes auf einen
Unterraum abbilden, beispielsweise
ein Punkt x des dreidimensionalen Raumes
V in eine Ebene U des gleichen Raumes V.
Der Raum der Befunde
Zimmermann (1975) hat ein einfaches
räumliches Modell aufgestellt, aus dessen
einziger Grundannahme die sogenannten
Axiome der traditionellen Theorie rein
logisch ableitbar sind. Er machte sich dabei
zunutze, daß geläufige statistische Parameter,
wie die Kovarianz, anschauliche geometrische
Repräsentationen besitzen.
Der Begriff des Raumes
Eine Menge von Elemente a, b,... , für die
eine kommutative ,assoziative und umkehrbare
Verknüpfung , die Summe,

Ist die Abbildung so gewählt, daß die
Differenz c des Bildes b = (x) und des
Urbildes x orthogonal zu allen Elementen
U ist, so spricht man von einer Projektion
auf U. Es gilt dann x = b c. Diese Zerlegung
von x ist eindeutig. Man sagt, diese
beiden Unterräume sind Orthogonalkomplemente
voneinander.
Ein für die Testtheorie wichtiger Satz
konstatiert die folgenden Gleichheiten:
a, b ab | a | | b | cos
(1.1)
1
n
i
i
m it 0 .
Daraus folgt ,daß das Skalarprodukt < a,b>
dividiert durch |a| uns |b| gleich dem cos
ist, also zwischen -1 und +1 liegt. Auf
Grund dieser Ungleichung kann man den
Korrelationskoeffizienten geometrisch
durch den Kosinus des von den Testvektoren
eingeschlossenen Winkels repräsentieren.
Auf diese Weise werden Tests als
Vektoren der Länge ihrer Standardabweichungen
in einer Richtung repräsentiert,
die durch ihre Korrelation mit Bezugstests
gegeben ist.
Summen von Zufallsgrößen
Werden die Zufallsgrößen X,Y : Ω →
als stets auf die Komponenten ω Ω, z. B.
Rohwertklassen, bezogen zusammengezählt,
so ist die Operation additiv:
(X Y)(ω) : = X(ω) +Y(ω) für jedes ω.
Beispiel: Sei X die Auswertung der einer
Aufgabensammlung der weiblichen Vpn.,
Y die entsprechende Auswertung der ännlichen,
so ist die Summe eine Zufallgröße,
über alle Personen. Sie besitzt Erwartungswert
und Varianz.
Produkte von X und Y
Der Begriff des (auf jede Ausprägung ω
der Zufallsgrößen X und Y bezogenen)
Produktes von Zufallsgrößen ist definiert.als
(X Y)(ω) := X(ω)Y(ω) für jedes ω.
Beispiel: Die Berechnung der Produktes
der Ergebnisse X und Y aus dem vorangegangenen
Beispiel. Auch hier ist der Bezug
wieder auf die Ausprägungen ω der Zufallsgrößen.
Produktbildung geht ein in die
Berechnung der Kovarianz
cov(X,Y) = (XY) - (X) (Y).
Zimmermann (1975)hat gezeigt, daß die
Repräsentation der Addition und Multiplikation
von Testergebnissen als reellwertige
Zufallsgrößen X über einem gemeinsamen
Wahrscheinlichkeitsraum < Ω, , > die
Grundbegriffe der klassischen Testtheorie
als die Eigenschaften einer geometrischen
extensiven Struktur repräsentierbar macht.
Sie gestattet eine besonders transparente
Darstellung der Theorie.
Ein (reeller) Hilbert-Raum
ist definiert als vollständiger linearer Vektorraum
über , in dem ein skalares Vektorprodukt
(X,Y) = Σ XY gegeben ist, bei
dem stets gilt (X,X) ≥ 0, und aus (X,X) = 0
folgt X = 0. Ein Beispiel ist der gewöhnliche
uns umgebende dreidimensionale
Raum. Bei den Anwendungen aus der
Testtheorie ist die Anzahl der Dimensionen,
über die bei der Skalarproduktbildung
zu summieren ist, meist gleich der Anzahl
der vorkommenden Testwerte. Ein dreidimensionales
Beispiel ist ein Test, dessen

Ergebnisse in der Menge Ω = { niedrig,
mittel, hoch} liegen. Kommen als Testergebnisse
die Zahlen von Null richtigen
Antworten bis 45 richtige Antworten vor
(Progressive Matrices Test), dann ist der
Raum von der Dimensionalität 46. Die
Dimensionalität kann bei kontinuierlichen
Testwerten, z.B. Reaktionszeiten, über alle
Grenzen wachsen. Vollständig bedeutet
dann, daß jede Cauchy-Folge von Vektoren
gegen einen festen Grenzvektor konvergiert.
Geometrische Interpretation der Kovarianz
als Skalarprodukt zweier Zufallsgrößen X
und Y.(Für diese Beispiel werden der einfachen
Schreibweise halber Erwartungswerte
von X = Y = 0 vorausgesetzt):
Anstelle von cov(X,Y) = XY kann man
wie in der Algebra schreiben cov(X,Y) =
||X|| ||Y|| cos . Unmittelbar ist ersichtlich,
dass nun die Standardabweichungen von X
und Y als Vektorlängen und die Korrelation
zweier Tests als Kosinus des von ihren
Vektoren eingeschlossenen Winkels repräsentiert
sind. Diese Repräsentation wird
meistens mehr als dreidimensional ausfallen,
weil die empirischen Winkel im Dreidimensionalen
nicht immer „passen“. Eine
Aufgabe der Theorie psychologischer
Diagnostik besteht in der Aufdeckung des
Zusammenhangs der beiden geometrischen
Repräsentationen.
Andere Aufgaben sind die Bestimmung der
Voraussetzungen, die ein Test besitzen
muß, um eine von Null verschieden Validität
erreichen zu können, Die Untersuchung
der Abhängigkeit dieser Voraussetzungen
von der Testlänge, die Konstruktion von
sogenannten Paralleltests, mit deren Hilfe
die Reproduzierbarkeit von Testergebnissen
an den gleichen Personen ohne erneute
Verwendung der gleichen Testaufgaben
möglich wird, und vieles mehr.
Historische Anmerkung.
Die psychologischen Diagnostik hat bereits
in der ersten Hälfte des zwanzigsten Jahrhunderts
versucht, eine geschlossene Theorie
zu entwickeln, die sich aus wenigen
Grundannahmen rein logisch ableiten läßt
Gulliksen, 1950, führt fünf solche Annahmen
auf, aus denen sich Antworten auf die
genannten Fragen und andere ableiten
lassen.Es sind dies – neben der Annahme
dass für alle vorkommenden Zufallsgrößen
Erwartungswerte und Varianzen existieren
und endliche Werte annehmen –
Fünf „Axiome“:
Die Zufallsgröße X , die das Testergebnis
ausmacht, ist in einen „wahren Wert“, T,
und eine Fehlerkomponente , E, additiv
dekomponierbar:
X = T + E.
E = 0, die Fehlerkomponente ist unsystematisch.
TE = 0, wahrer Wert und Fehler korrelieren
nicht.
E1E2 = 0, Fehler in verschiedenen Tests
korrelieren nicht,
E1T21 = 0, Fehler eines Tests korrelieren
nicht mit dem wahren Wert eines anderen
Tests.
Der „wahre“ Wert
Die klassische Testtheorie faßt den Erwartungswert
( Mx | B) der „wahren“ Werte,
als gleich dem stets existierenden Erwartungswert
der („Roh-“)Werte X auf. ( Mx
| B ) = ( X | B) für alle B . Dabei ist
B die Menge der Antwortmuster.
„Wahrer“ Wert einer Person
Um diesen zu finden, muß man mittels f
eine Person α aus der Menge Φ wählen und
dann über deren Menge γ (α) von Antwortmustern
Mx(ω) = ( (X | γ (α) ) für
jedes ω Ω bestimmen. Die Größe Mx ist
auf die Person bezogen konstant. Sie ist
gleich ihrem Erwartungswert.
Die Bestimmung von Mx als Operator

Mx = (X | f) o f ist eine zusammengesetzte
Abbildung, wobei X und f über dem
gleichen Wahrscheinlichkeitsraum definiert
sind. Nur auf die B bedingt, macht
Mx aus der Zufallsgröße X eine neue Zufallsgröße
Mx, im Raum aus einem Vektor
einen neuen. Man spricht deshalb von einem
Operator Mx.
Mx ein linearer Operator
Kovarianzen
cov(Mx,Y) = cov(X,My) = cov(Mx,My),
weil (MxY) = (Mxy) = (MxMy)
= (MxMy ) = (XMy). Weiterhin gilt
cov(Mx,Y) = (MxY) - ( (Mx)) (Y) =
(MxMy) - ((Mx))((My)) =
cov(Mx,My).
Es gilt Mx+y(ω) = ( X + Y | γ(ω))
= ( X | γ(ω)) + ( Y | γ(ω))
= Mx(ω) + My(ω), für jedes
ω Ω
und deshalb Additivität
Mx+y = Mx + My,
außerdem Homogenität
Mαx = α Mx, für alle α .
Reliabilität als True-Score Anteil
Satz 1: ² (X, Mx) = var(Mx) / var(X).
Beweis: Einsetzen von
cov(Mx,X) = cov(Mx,Mx) = var(Mx)
in die Definition von
² := cov(X, Mx)²/ (var(X)var(Mx)).
Sonderfall: Konstanten
Sei Y eine auf jeder Äquivalenzklasse von
Ω konstante Zufallsgröße.
Dann gilt wegen der Linearität
Mxy(ω) = ( XY | (ω) )
=(X| (ω) ) Y(ω)
=Mx (ω) Y(ω), für jedes ω Ω
und deshalb Mxy = Mx Y.
Wegen ( Mx | Ω) = ( X | Ω)
gilt ( Mx ) = (X). Außerdem
Mx-x = Mx - ( Mx).
Validität höchstens gleich Reliabilität
Satz 2: (X, My) (X, Mx).
Beweis: Wegen cov(Mx,My)²
var(Mx)var(My),
der Schwarzschen Ungleichung, und wegen
cov(Mx,Y) = cov(X,My)
nach Einsetzen unter Benutzung von Satz
1.
Bedingt unabhängige Zufallsgrößen
X1 und X2 sind bedingt unabhängige Zufallsgrößen
in Bezug auf f, wenn für alle
(ω) B aus < Ω, , > die Zufallgrößen
X1 | (ω) und X2 | (ω) unabhängig
sind. Für sie ist die bedingte Erwartung

ihres Produkts gleich dem Produkt ihrer
bedingten Erwartungen:
Satz: Mx1x2 = Mx1 Mx2,
Beweis: Wegen
Mx1x2 = (X1X2| (ω))
= (X1 |(ω))( X2 |(ω))
=Mx1(ω)Mx2(ω), für jedes ω Ω.
Paralleltests
Zufallsgrößen X1 und X2 sind bedingt auf
f identisch verteilt, wenn für alle D Λdie
Zufallsgrößen X1|D und X2|D identisch
verteilt sind, d. h., die induzierten Wahrscheinlichkeitsverteilungen
Px1|D und
PX2|D sind gleich.
Wenn dies für X1 und X2 der Fall ist, so
gilt Mx1 = Mx2, aber nicht ohne weiteres
die Umkehrung.
Paralleltest-Korrelation als Reliabilität
Satz 3: Seien X1 und X2 bedingt unabhängige,
bedingt identisch verteilte Zufallsgrößen.
Dann gilt
ρ(X1,X2) = var(Mx1) / var (X1).
Beweis:
cov(X1,X2)=X1X2 - X1X2
=Mx1x2 - Mx1 Mx2, wegen Mx =
X,
=Mx1,Mx2 - Mx1Mx2, wegen Mx1x2
= Mx1Mx2,
=cov(Mx1,Mx2) = var(Mx ) = var(Mx2),
und Einsetzen in
(X1,X2) = cov(X1,X2)/(X1X2)
Def.: Zufallsgrößen X1 und X2 sind bezogen
auf f bedingt unkorreliert, wenn für
alle D Λ die Zufallsgrößen X1|D und
X2|D unkorreliert sind, d. h.
cov(X1|D,X2|D) = 0.
Bedingt unabhängige Zufallsgrößen sind
bedingt unkorreliert, aber i. a. nicht umgekehrt.
X1 und X2 sind bedingt unkorreliert,
gdw. Mx1x2 = Mx1 Mx2.
Testverlängerung durch parallele
Teile
Satz 4: Seien X1, X2, ...Xn bedingt unabhängige,
bedingt identisch verteilte Zufallsgrößen
und Sn = X1 + X2 + ... + Xn.
Es gilt
ρ²(Sn,Msn)
= n ρ²(X1,Mx) /[1 +(n-1) ²(X1,Mx1)].
Beweis: Da X1, X2, ...Xn bedingt unabhängig
und bedingt identisch verteilt sind,
gilt cov(Xi,Xj)=cov(Mxi,Mxj)=var(Mx1)
für i,j=1,2,...,n. Außerdem gilt,
wie im Beweis von Satz 3 Var(Sn)=
Σvar(Xi)+cov(Xi,Xj)=n var(X1)+n (n-
1)var(Mx1),
und var((Msn)= n² var(Mx1). Wegen
ρ²(Sn,Msn) = var(Msn/var(Sn) und
ρ²(X1,Mx1)= var(Mx1)/varX1) nach Einsetzen
gilt wegen ²(X,Mx) = var(Mx)/
var(X) die Behauptung.
Der Meßfehler
Def: Das Komplement der bedingten Erwartung
von X bezogen auf f ist eine Zufallsgröße
(X – Mx) : Ω , gegeben durch
(X - Mx)() =X() –Mx(), für jedes
Ω.
Bezeichnet man den Identitätsoperator mit
1, so lässt sich 1 – M als der Operator auffassen,
der aus der Zufallsgröße X die Zufallsgröße
X – Mx macht. Mx-Mx =0 wegen
MMx= Mx und

Mx-Mx = (X – Mx) = 0, wegen Mx
= X.
True-score und Fehler unkorreliert
Weiterhin gilt
[(X – Mx)Y] = (XY)-(MxY) =
(XY) - (XMy) = [X(Y-My)], und
[(X-Mx)(y – My)] = (XY) - (MxMy)
= (XY)- (MxY). Weil (X – Mx) = (Y
– My) = 0,
ist hierdurch bewiesen, daß cov(X –
Mx),Y) =cov(X,Y – My)=cov(X – Mx,Y –
My),
speziell:
cov(X – Mx,X) = cov(X-Mx,Y – My) =
var(X – Mx).
Außerdem: cov(X – Mx,My) = cov(X,My
– MMy) = cov(X,0) = 0. Also:
Cov(X-Mx,Mx) = 0.
Geometrische Repräsentation
und m Testwiederholungen, ist L2() ein
n-dimensionaler Euklidischer Raum und
L2() ein m-dimensionaler Unterraum.
Das Skalarprodukt zweier auf den Erwartungswert
bezogenen Zufallsgrößen ist ihre
Kovarianz
< (X - X, Y - Y > = cov(X,Y).
Standardabweichung entspricht der
Vektorlänge
Die Norm einer auf ihren Erwartungswert
bezogene Zufallsgröße ist ihre Standardabweichung.
|| X - X || = X .
Für eine Zufallgröße X L2() ist die
bedingte Erwartung Mx durch die Projektion
von X auf L2() gegeben.
Fehlerverteilung als othogonale
Projektion
Das Komplement der bedingten Erwartung
X – Mx ist die Projektion von X auf
das orthogonale Komplement von L2().
Sei < Ω, , > ein Wahrscheinlichkeitsraum
und eine -Algebra, die
durch den zufälligen Punkt f : Ω induziert
ist. Sämtliche Zufallgrößen mit endlicher
Varianz, die auf < Ω, , > definiert
sind, bilden den Hilbert-Raum L2().
Er besitzt das Skalarprodukt < X1, X2 > =
(X1X2) und die Norm ||X|| = X² .
L2() bildet einen abgeschlossenen Unterraum
von L2().
Bei endlichen Wahrscheinlichkeitsräumen,
wenn Ω n Elemente und m
Elemente enthält, also z. B. bei N Tests
Der Operator M, der jedem X seine bedingte
Erwartung Mx zuordnet, und der
Operator 1 – M , der jedem X das Komplement
der bedingten Erwartung X - M
zuordnet, sind orthogonale Projektionen.
X² = T² + E² als Satz des Pythagoras
Jede Zufallsgröße X L2() ist die eindeutige
Summe einer Zufallgröße Mx im
Unterraum L2() und einer Zufallsgröße X
– Mx im orthogonalen Komplement von
L2(). Es gilt
||X||² = || Mx ||² + || X – Mx ||² ,

das bedeutet var(X) = var (Mx) + Var ( X –
Mx).
MMx = Mx und ( 1 – M)x-Mx = X –M
gelten, weil Projektionsoperatoren die Eigenschaft
der Idempotenz besitzen.
Mx-Mx = 0 und ( 1 –M)Mx =0 weil beide
Male das orthogonale Komplement eines
Unterraumes auf den Nullvektor projiziert
wird.
True-score und Fehler unkorreliert
Daß cov (Mx Y – My) = 0, oder daß der
wahre Wert eines Tests mit dem Fehlerwert
eines anderen Tests unkorreliert ist,
gilt, weil jeder Vektor in L2() orthogonal
zu jedem Vektor im othogonalen Komplement
von L2() ist.
Die Gleichheit cov(X, Mx) = var(Mx) entspricht
< X - X, Mx-x> = || X – Mx||² , und
cov((X, X-Mx) = var (X-Mx) wegen < X -
X, X –Mx> = || X – Mx ||². Das sind Eigenschaften
aller orthogonaler Projektionen.
Traditionelle Darstellung der gleichen
Sachverhalte
Die Überslegenheit des zeitgenössischen
Zugangs wird besonders deutlich, wenn
man diese Ergebnisse in traditioneller Weise
ableitet, wie es z. B. Gulliksen (1950)
tut:
Paralleltest-Korrelation
Zu diesem Zweck werden Paralleltests so definiert,
daß ihre Interkorrelation gleich der Reliabilität
wird: (Mindestens) drei Tests sind parallel, wenn
Sie gleiche Erwartungswerte , gleiche Varianzen
und gleiche Interkorrelationen aufweisen und die
True-Scores der Personen gleich sind.
Paralleltestkorrelation gleich Reliabilität
ρ xx´= T²/ X²
cov( X , X ´) cov( X , X ´)
XX ´ 2
X X ´
X
cov( X , X ´) E ( X * X ´) E ( X ) E ( X ´),
E ( X * X ´) E (( T e) * ( T ´ e´))
E ( TT ´ Te´ eT ´ ee´) E ( TT ´) E ( Te´)
E ( eT ´) E ( ee´). E ( X ) E ( X ´)
E ( T e) * E ( T e´) E ( T ) E ( T )
E ( T ) E ( e) E ( e´) E ( T ) E ( ee´).
cov( X , X ´ ) ²( T )
Varianzverdoppelung i. a. nicht additiv
2
x y
E (( X Y )²) ( E ( X Y ))²
E ( X ² 2 XY Y ²)
( E ( X )² 2 E ( X ) E ( Y ) E ( Y )²)
E ( X ²) 2 E ( XY ) E ( Y ²)
E ( X )² 2 E ( x) E ( Y ) E ( Y )²
2 2 2 2
2 cov( X , Y ) 2
x y x y x y xy
Reliabilität bei doppelter Testlänge
Varianzen bei doppelter Länge
´ ´
x y , x y
x y ´ ´
x y
´ ´
cov( X Y , X Y )
´ ´
1, 2 , 1 2
cov(2T e e 2 T e e )
2
x y
cov(2 T, 2 T )
2 2
x y
x y xy
2 cov( , ) (1 )
Zu beachten ist, daß sich bei doppelter Länge die
True-Varianz vervierfacht, während sich die Fehler-
Varianz nur verdoppelt. Dieser quadratische Anstieg
gegenüber einem linearen bringt den Gewinn
an Reliabilität und gilt auch bei allgemeiner Testverlängerung
um das n-fache.
Reliabilität bei n-facher Testlänge
n n n
X Y , e e , T T
i i i
i 1 i 1 i 1
n n n
2
x
2
Yi YiYj
i 1 i 1 j 1
,
j
2
i
xy
n n n
2
Yi TiTj Ti Tj
i 1 i 1 j 1
,
j
i

Bei Parallelität wird daraus wegen
2 2
n n
x y yy´
[1 ( 1) ]
2 2
n ²
T
T1
2 2
n
e
e1
Spearman-Brown (1907):
YY ´
n
Y 1Y
1 '
1 ( n 1)
Y 1Y
1 '
Reliabilität und Testlänge graphisch
Man sieht, dass auch diese Darstellung
schlüssig ist, selbst wenn sie auf Voraussetzungen
begründet ist, die sich aus dem
Zimmermannschen (1975) Ansats als Sätzt
ableiten lassen.
Literatur
Bamberg, G. (1972). Statistische Entscheidungstheorie.
Würzburg: Physica-Verlag.
Bosch, K. (1976). Elementare Einführung
in die Wahrscheinlichkeitsrechnung. Reinbeck:
Rowohlt.
Bosch, K. (1982). Elementare Einführung
in die angewandte Statistik. Braunschweig:
Vieweg.
Testlänge und Validität
2
X
k
, Y
l
2
2 2
X
k
Validität:Verlängerung nur des Tests
X
2
k
, Y
( X , Y )
1 ( k 1) ( X , X ') 1 ( l 1) ( Y , Y ')
2
X
k
, Y
k
2
kl
2
( X , Y )
X
Validität und Testlänge n graphisch für verschiedene
Reliabilitäten
l
Y
2 2
X
k
1 ( k 1) ( X , X ')
k
l
, Y
Y
Fischer, G. (1974). Einführung in die
Theorie psychologischer Tests. Bern: Huber.
(Kap. 1 - 19).
Gulliksen, H. Theory of Mental Tests, New
York, Wiley, 1950.
Lord, F. M. & Novick, M. R. : Statistical
Theories of Mental Test Scores.Reading,
Addison-Wesley, 1968.
Zimmerman, D. W. : Probability Space,
Hilbert Space and the Axioms of Test Theory.
Psychometrika, 40, (3) 395 – 412,
1975
Lindgren, B.W. (1971). Elements of decision
theory. New York: MacMillan.
(Wird fortgesetzt.)