Integralrechnung und Vektoren

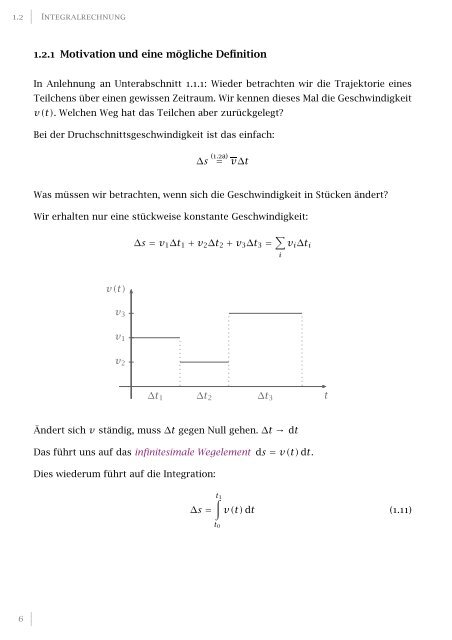
∆s=v 1 ∆t 1 +v 2 ∆t 2 +v 3 ∆t 3 = ∑ i1.2∣ Integralrechnung1.2.1 Motivation und eine mögliche DefinitionIn Anlehnung an Unterabschnitt 1.1.1: Wieder betrachten wir die Trajektorie einesTeilchens über einen gewissen Zeitraum. Wir kennen dieses Mal die Geschwindigkeitv(t). Welchen Weg hat das Teilchen aber zurückgelegt?Bei der Druchschnittsgeschwindigkeit ist das einfach:∆s (1.2a)= v∆tWas müssen wir betrachten, wenn sich die Geschwindigkeit in Stücken ändert?Wir erhalten nur eine stückweise konstante Geschwindigkeit:v i ∆t itv(t)v 3∆t 1 ∆t 2 ∆t 3v 1v 2Ändert sichv ständig, muss∆t gegen Null gehen.∆t→ dtDas führt uns auf das infinitesimale Wegelement ds=v(t) dt.Dies wiederum führt auf die Integration:∆s=∫t 1t 0v(t) dt (1.11)6∣

Differential- und Integralrechnung für Funktionen einer Veränderlichen∣ 1Das Integralb∫ b∫I= f(x) dx=a adxf(x) (1.12)ist über einen Grenzwertprozess definiert.Betrachte dazu:f(x)ξ 1 ξ 2 ξ 3 ξ 4 ξ 5xDas Intervalla≤x≤bwird innkleine Intervallea

1.2∣ Integralrechnungf(x)∆x ∆x . . .xEigenschaften des bestimmten Integralsb∫0 dx=0 (1.15a)aa∫f(x) dx=0(1.15b)aa∫ b∫f(x) dx=− f(x) dx(1.15c)b ac∫ b∫ c∫f(x) dx= f(x) dx+ f(x) dx(1.15d)a a bb∫b∫ b∫(af(x)+bg(x)) dx=a f(x) dx+b g(x) dx (1.15e)aa a1.2.2 Die Stammfunktiona) Definitionx∫Betrachte die FunktionF(x)= f(u) du und deren Ableitung.a8∣

Differential- und Integralrechnung für Funktionen einer Veränderlichen∣ 1Betrachte dazu zuerst:Daraus folgt dann:F(x+∆x)=x+∆x ∫af(u) du (1.15d)=x∫f(u) du+a=F(x)+x+∆x ∫xx+∆x ∫xf(u) duf(u) du(1.16a)und die Ableitung lautet:F(x+∆x)−F(x) (1.16a)=x+∆x ∫xf(u) dud F(x+∆x)−F(x)F(x)= limdx ∆x→0 ∆x(1.16b)= lim∆x→0x+∆x ∫xf(u) du∆x(1.16b)(1.14) f(x)∆x= lim =f(x) (1.17)∆x→0 ∆xMit diesem Ergebnis definiert man die Stammfunktion oder das unbestimmte Integral:∫F(x)= f(x) dx (1.18)F(x) ist immer dann Stammfunktion vonf(x), wenn gilt dF(x)dx=f(x). Die Funktionf(x) hat unendlich viele Stammfunktionen, denn wenn F(x) Stammfunktion ist,dann auchG(x)=F(x)+c.b) Beziehung zum bestimmten IntegralNotation:b∫af(x) dx=F(b)−F(a)=[F(x)] b a =F(x)|b a∣ 9

1.2∣ Integralrechnungc) Wichtige Stammfunktionen∫a dx=ax+c(1.20a)∫ax n dx= an+1 xn+1 +c (1.20b)∫e ax dx= 1 a eax +c(1.20c)∫ adx=a ln(x)+cx (1.20d)∫a cos(bx) dx= a b sin(bx)+c∫a sin(bx) dx=− a b cos(bx)+c(1.20e)(1.20f)1.2.3 IntegrationsregelnIntegrale können schnell kompliziert werden. Die beiden folgenden Regeln könnenhelfen, das Integral zu vereinfachen um es so besser zu berechnen.a) SubstitutionBeispiel 1:∫1I= √ dx wird substituiert durch die Regely= arcsin(x),x= sin(y).1−x2Wir wissen, dass dxdy= cos(y), also dx= cos(y) dy∫ ∫cos(y) dyI= √ = dy=y+c= arcsin(x)+c (1.21)1−sin 2 (y)10∣

Differential- und Integralrechnung für Funktionen einer Veränderlichen∣ 1Beispiel 2:Wichtig ist die Grenzen auch zu substituieren.I=∫x 1x exp(ax 2 ) dxx 0 ∣∣x 2 =u⇒x= √ u,=x∫12x 2 0√u exp(au)du2 √ ududu=2x⇝ dx=dx 2x = du2 √ u= 1 2x∫12exp(au) dux 2 0= 12a exp(au) ∣ ∣∣∣ x 2 1x02∣x 1= 12a exp(ax2 )∣x 0Formale Regel der Integration durch Substitution:b∫adyf(y) =g −1 ∫(b)y=g(x)g −1 (a)dxg ′ (x)f(g(x)) (1.22)b) Partielle IntegrationFormale Regel der partiellen Integration:b∫b∫f ′ (x)g(x) dx=f(x)g(x)| b a − f(x)g ′ (x) dx (1.23)aa∣ 11

1.2∣ IntegralrechnungHerleitung:∫∫f(x)g(x)= (f(x)g(x)) ′ dx∫= (f ′ (x)g(x)+f(x)g ′ (x)) dx∫ ∫= f ′ (x)g(x) dx+ f(x)g ′ (x) dx∫f ′ (x)g(x) dx=f(x)g(x)− f(x)g ′ (x) dx∫∣∣− f(x)g ′ (x) dxBeispiele:∫∫lnx dx=1 lnx= x lnxf ′ (x) g(x)f(x) g(x)∫−=x lnx−x+cx1xf(x)g ′ (x)dx∫xsinxf(x) g ′ (x)dx= xf(x)(− cosx)g(x)∫+1f ′ (x)=−x cosx+ sinx+ccosx dxg(x)12∣

•Potenzreihenentwicklung∣ 22 PotenzreihenentwicklungAls Potenzreihe bezeichnet man eine unendliche konvergente Reihe der Form∞∑a n (x−x 0 ) n .n=12.1 Bedeutung in der PhysikPotenzreihen sind ein wichtiges Näherungsverfahren in der Physik. Sie kommen immerzur Anwendung, wenn eine Funktionf(x) nur in einer kleinen Umgebung umeinen Punktx 0 ausgewertet werden muss.Beispiel: Eine Masse schwingt um das Minimum eines komplizierten Potentials. Wielautet die Schwingungsfrequenz? Zur Beantwortung dieser Frage reicht es aus, dieFunktionv(x) in der Nähe des Minimums zu kennen. Annäherung durch z.B. eineParabel:v(x)x 0xWas wird durch Potenzreihen einfacher?Sei die Funktionf(x) beliebig kompliziert.∣ 13

2.2∣ TaylorreihePotenzreihe:f P (x)=a 0 +a 1 (x−x 0 )+a 2 (x−x 0 ) 2 +a 3 (x−x 0 ) 3 +...+a j (x−x 0 ) j +...∞∑= a n (x−x 0 ) n (2.1)n=0Oft reicht es für eine lokale Umgebung vonx 0 (x−x 0 ist klein), niedrige Potenzenzu betrachten:f P,2 (x)=a 0 +a 1 (x−x 0 )+a 2 (x−x 0 ) 2(quadratische Näherung)f P,2 (x) ist meist wesentlich einfacher und macht das Integrieren, Lösen von Differentialgleichungen,etc. einfacher oder überhaupt erst möglich.2.2 TaylorreiheWie sieht eine Potenzreihef P (x) einer Funktionf(x) umx=x 0 aus?f P (x) (2.1)=∞∑a n (x−x 0 ) nn=0Setzex=x 0 . Aus der Forderungf(x 0 )=f P (x 0 ) und ausf P (x 0 )=a 0 +0 folgt:a 0 =f(x 0 )(2.2a)Es muss auch geltenf ′ (x 0 )=f ′ P (x 0):Weiterhin:∞ f P ′ (x)= ∑a n n(x−x 0 ) n−1n=1f ′ P (x 0)=a 1!=f ′ (x 0 ) (2.2b)f ′′P (x)= ∞ ∑n=2f ′′P (x 0)=2a 2!=f ′′ (x 0 )a n n(n−1)(x−x 0 ) n−2odera 2 = 1 2 f′′ (x 0 )(2.2c)14∣

Potenzreihenentwicklung∣ 2Fortsetzen des Verfahrens führt auf die Formel von Taylor:f P (x)=∞∑n=01n! f(n) (x 0 )(x−x 0 ) n (2.3)Anmerkungen: Hier wurde vorrausgesetzt, dass die Potenzreihe existiert und f(x) beliebigof differenzierbar ist. Eine Potenzreihe muss nicht immer konvergieren. Meist ist die Konvergenznur innerhalb eines Konvergenzradius gegeben, d.h. für|x−x 0 |

2.3∣ Beispielef(x)=e x f(x)=e x , x 0 =0f (n) (x)=e x , f (n) (x 0 )=1Taylorreihe:e x =∞∑n=0x nn!(2.5)Konvergiert fürx∈RWeitere Beispiele:sin(x)=∞∑n=0, x∈R (2.6)(2n+1)!(−1) n x2n+1cos(x)=∞∑n=0(−1) n x2n, x∈R (2.7)(2n)!ln(1+x)=∞∑n=1(−1) n+1xn, −1

Vektoren∣ 66 VektorenUnter einem Vektor versteht man in der analytischen Geometrie ein Objekt, das eineParallelverschiebung im Raum beschreibt.6.1 Notwendigkeit und DarstellungWir kennen physikalische Größen, die nur einen Wert haben, zum Beispiel: Masse, Energie, Druck, . . . → SkalareDaneben gibt es solche, die zusätzlich von ihrer Richtung abhängen, zum Beispiel: Kraft, Geschwindigkeit, . . .Zur Darstellung verwenden wir einen Pfeil im Raum, dessen Länge den Betrag derphysikalischen Größe beschreibt. Die Länge eines Vektors wird Betrag genannt.v 1v 2In diesem Bild kann man zwei Rechenoperationen einführen: Addition∣ 53

6.2∣ Basis und Koordinatensystema+baba+b=b+a(a+b)+c=a+(b+c) Skalare Multiplikation:λa2aaFür Vektoren gibt es mehrere Schreibweisen.Pfeil:Unterstrich:Fett:a, ⇀ aaa6.2 Basis und Koordinatensystem6.2.1 BasisvektorenIm dreidimensionalen können wir jeden Vektor als Linearkombination von drei Basisvektorendarstellen:54∣