Rigid Body Analysis in a Plane: The Most ... - MAELabs UCSD
Rigid Body Analysis in a Plane: The Most ... - MAELabs UCSD
Rigid Body Analysis in a Plane: The Most ... - MAELabs UCSD
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Translation<br />
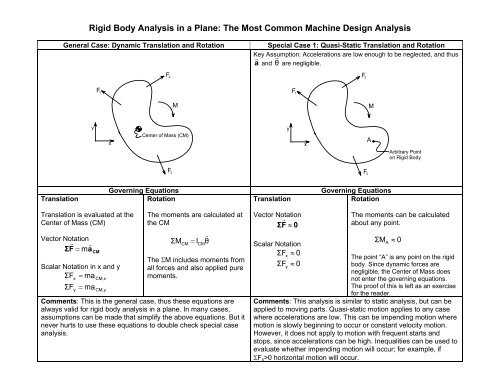
<strong>Rigid</strong> <strong>Body</strong> <strong>Analysis</strong> <strong>in</strong> a <strong>Plane</strong>: <strong>The</strong> <strong>Most</strong> Common Mach<strong>in</strong>e Design <strong>Analysis</strong><br />
General Case: Dynamic Translation and Rotation Special Case 1: Quasi-Static Translation and Rotation<br />
Key Assumption: Accelerations are low enough to be neglected, and thus<br />
a r and θ & are negligible.<br />
y<br />
F1<br />
Translation is evaluated at the<br />
Center of Mass (CM)<br />
Vector Notation<br />
r r<br />
ΣF<br />
= ma<br />
CM<br />
Scalar Notation <strong>in</strong> x and y<br />
ma ΣF =<br />
x<br />
ma ΣF =<br />
y<br />
CM, x<br />
CM, y<br />
x<br />
F2<br />
F3<br />
M<br />
Center of Mass (CM)<br />
Govern<strong>in</strong>g Equations Govern<strong>in</strong>g Equations<br />
Rotation<br />
Translation<br />
Rotation<br />
<strong>The</strong> moments are calculated at<br />
the CM<br />
ΣMCM = ICMθ&<br />
&<br />
<strong>The</strong> ΣM <strong>in</strong>cludes moments from<br />
all forces and also applied pure<br />
moments.<br />
Comments: This is the general case, thus these equations are<br />
always valid for rigid body analysis <strong>in</strong> a plane. In many cases,<br />
assumptions can be made that simplify the above equations. But it<br />
never hurts to use these equations to double check special case<br />
analysis.<br />
y<br />
F1<br />
Vector Notation<br />
r<br />
ΣF ≈ 0<br />
Scalar Notation<br />
ΣFx ≈ 0<br />
ΣFy ≈ 0<br />
x<br />
F2<br />
F3<br />
M<br />
A<br />
Arbitrary Po<strong>in</strong>t<br />
on <strong>Rigid</strong> <strong>Body</strong><br />
<strong>The</strong> moments can be calculated<br />
about any po<strong>in</strong>t.<br />
ΣM A ≈<br />
0<br />
<strong>The</strong> po<strong>in</strong>t “A” is any po<strong>in</strong>t on the rigid<br />
body. S<strong>in</strong>ce dynamic forces are<br />
negligible, the Center of Mass does<br />
not enter the govern<strong>in</strong>g equations.<br />
<strong>The</strong> proof of this is left as an exercise<br />
for the reader.<br />
Comments: This analysis is similar to static analysis, but can be<br />
applied to mov<strong>in</strong>g parts. Quasi-static motion applies to any case<br />
where accelerations are low. This can be impend<strong>in</strong>g motion where<br />
motion is slowly beg<strong>in</strong>n<strong>in</strong>g to occur or constant velocity motion.<br />
However, it does not apply to motion with frequent starts and<br />
stops, s<strong>in</strong>ce accelerations can be high. Inequalities can be used to<br />
evaluate whether impend<strong>in</strong>g motion will occur; for example, if<br />
ΣFx>0 horizontal motion will occur.
Special Case 2: Dynamic Rotation about a Pivot Special Case 3: Quasi-Static Rotation about a Pivot<br />
Key Assumption: Accelerations are low enough to be neglected, and thus<br />
a r and θ & are negligible.<br />
y<br />
F1<br />
x<br />
Rotation θ<br />
F2<br />
P (pivot)<br />
F3<br />
M<br />
Govern<strong>in</strong>g Equations<br />
<strong>The</strong> moments and <strong>in</strong>ertia are calculated about the pivot<br />
= I &θ<br />
&<br />
ΣM P P<br />
ΙP = Moment of Inertia about pivot po<strong>in</strong>t P.<br />
Comments:<br />
• <strong>The</strong> direction of positive rotation is shown as counterclockwise<br />
to be consistent with the right-hand rule.<br />
• <strong>The</strong> moment of <strong>in</strong>ertia of a mach<strong>in</strong>e element can be difficult to<br />
calculated, but often can be estimated by summ<strong>in</strong>g key<br />
masses on the object multiplied by the distance to the pivot<br />
squared.<br />
y<br />
F1<br />
x<br />
Rotation θ<br />
F2<br />
P (pivot)<br />
F3<br />
M<br />
Govern<strong>in</strong>g Equations<br />
<strong>The</strong> moments are calculated about the pivot<br />
ΣM P ≈ 0<br />
Comments:<br />
• Impend<strong>in</strong>g motion can be calculated with an <strong>in</strong>equality, for<br />
example ΣMP>0 <strong>in</strong>dicates that counterclockwise motion will<br />
occur.<br />
• Special case 3 is a subset of special case 1. <strong>The</strong> force balance<br />
equation are still valid, and can be used to calculate the<br />
reaction forces at the pivot.