Discrete Mathematics University of Kentucky CS 275 Spring ... - MGNet

Discrete Mathematics
University of Kentucky CS 275
Spring, 2007
Professor Craig C. Douglas
http://www.mgnet.org/~douglas/Classes/discrete-math/notes/2007s.pdf
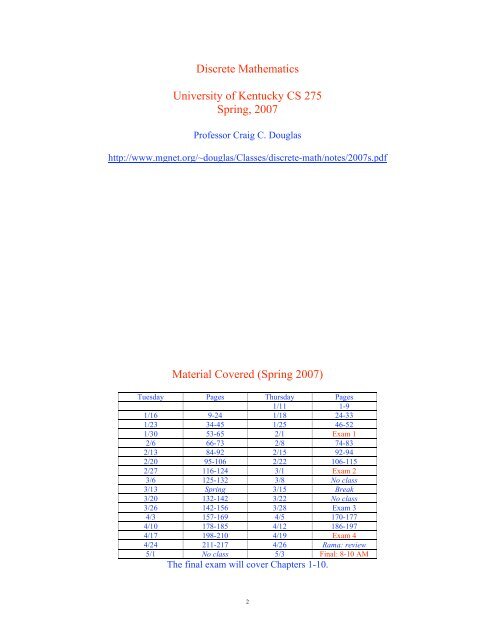
Material Covered (Spring 2007)
Tuesday Pages Thursday Pages
1/11 1-9
1/16 9-24 1/18 24-33
1/23 34-45 1/25 46-52
1/30 53-65 2/1 Exam 1
2/6 66-73 2/8 74-83
2/13 84-92 2/15 92-94
2/20 95-106 2/22 106-115
2/27 116-124 3/1 Exam 2
3/6 125-132 3/8 No class
3/13 Spring 3/15 Break
3/20 132-142 3/22 No class
3/26 142-156 3/28 Exam 3
4/3 157-169 4/5 170-177
4/10 178-185 4/12 186-197
4/17 198-210 4/19 Exam 4
4/24 211-217 4/26 Rama: review
5/1 No class 5/3 Final: 8-10 AM
The final exam will cover Chapters 1-10.
2

Course Outline
1. Logic Principles
2. Sets, Functions, Sequences, and Sums
3. Algorithms, Integers, and Matrices
4. Induction and Recursion
5. Simple Counting Principles
6. Discrete Probability
7. Advanced Counting Principles
8. Relations
9. Graphs
10. Trees
11. Boolean Algebra
12. Modeling Computation
3
Logic Principles
Basic values: T or F representing true or false, respectively. In a computer T an
F may be represented by 1 or 0 bits.
Basic items:
• Propositions
o Logic and Equivalences
• Truth tables
• Predicates
• Quantifiers
• Rules of Inference
• Proofs
o Concrete, outlines, hand waving, and false
4

Definition: A proposition is a statement of a true or false fact (but not both).
Examples:
• 2+2 = 4 is a proposition because this is a fact.
• x+1 = 2 is not a proposition unless a specific value of x is stated.
Definition: The negation of a proposition p, denoted by ¬p and pronounced not
p, means that, “it is not the case that p.” The truth values for ¬p are the opposite
for p.
Examples:
• p: Today is Thursay, ¬p: Today is not Thursday.
• p: At least a foot of snow falls in Boulder on Fridays. ¬p: Less than a foot
of snow falls in Boulder on Fridays.
5
Definition: The conjunction of propositions p and q, denoted p!q, is true if
both p and q are true, otherwise false.
Definition: The disjunction of propositions p and q, denoted p"q, is true if
either p or q is true, otherwise false.
Definition: The exclusive or of propositions p and q, denoted p#q, is true if
only one of p and q is true, otherwise false.
Truth tables:
p ¬p q p!q p"q p#q
T F T T T F
T * F * F F T T
F * T * T F T T
F T F F F F
* The truth table for p and ¬p is really a 2$2 table.
6

Concepts so far can be extended to Boolean variables and Bit strings.
Definition: A bit is a binary digit. Hence, it has two possible values: 0 and 1.
Definition: A bit string is a sequence of zero or more bits. The length of a bit
string is the number of bits.
Definition: The bitwise operators OR, AND, and XOR are defined based on
!, ", and #, bit by bit in a bit string.
Examples:
• 010111 is a bit string of length 6
• 010111 OR 110000 = 110111
• 010111 AND 110000 = 010000
• 010111 XOR 110000 = 100111
7
Definition: The conditional statement is an implication, denoted p%q, and is
false when p is true and q is false, otherwise it is true. In this case p is known
as a hypothesis (or antecedent or premise) and q is known as the conclusion
(or consequence).
Definition: The biconditional statement is a bi-implication, denoted p&q, and
is true if and only if p and q have the same truth table values.
Truth tables:
p q p%q p&q
T T T T
T F F F
F T T F
F F T T
8

We can compound logical operators to make complicated propositions. In
general, using parentheses makes the expressions clearer, even though more
symbols are used. However, there is a well defined operator precedence
accepted in the field. Lower numbered operators take precedence over higher
numbered operators.
Examples:
• ¬p!q = (¬p) !q
• p!q"r = (p!q) "r
Operator Precedence
¬ 1
! 2
" 3
% 4
& 5
9
Definition: A compound proposition that is always true is a tautology. One that
is always false is a contradiction. One that is neither is a contingency.
Example:
p ¬p p!¬p p"¬p
T F F T
F T F T
contigencies contradiction tautology
Definition: Compound propositions p and q are logically equivalent if p&q is a
tautology and is denoted p'q (sometimes written as p!q instead).
10

Theorem: ¬(p"q) ' ¬p ! ¬q.
Proof: Construct a truth table.
p q ¬(p"q) ¬p ¬q ¬p!¬q
T T F F F F
T F F F T F
F T F T F F
F F T T T T
qed
Theorem: ¬(p!q) ' ¬p " ¬q.
Proof: Construct a truth table similar to the previous theorem.
These two theorems are known as DeMorgan’s laws and can be extended to any
number of propositions:
¬(p 1 "p 2 "…"p k ) ' ¬ p 1 ! ¬ p 2 ! … ! ¬ p k
¬(p 1 !p 2 !…!p k ) ' ¬ p 1 " ¬ p 2 " … " ¬ p k
11
Theorem: p%q ' ¬p"q.
Proof: Construct a truth table.
p q p%q ¬p ¬p"q
T T T F T
T F F F F
F T T T T
F F T T T
qed
These proofs are examples are concrete ones that are proven using an exhaustive
search of all possibilities. As the number of propositions grows, the number of
possibilities grows like 2 k for k propositions.
The distributive laws are an example when k=3.
12

Theorem: p" (q!r) ' (p"q)!(p"r).
Proof: Construct a truth table.
p q r p" (q!r) p"q p"r (p"q)!(p"r)
T T T T T T T
T T F T T T T
T F T T T T T
T F F T T T T
F T T T T T T
F T F F T F F
F F T F F T F
F F F F F F F
qed
Theorem: p! (q"r) ' (p!q) " (p!r).
Proof: Construct a truth table similar to the previous theorem.
13
Some well known logical equivalences includes the following laws:
'
p!T'p
p"F'p
p"T'T
p!F'F
p"p'p
p!p'p
¬(¬p) 'p
p"¬p 'T
p!¬p 'F
p"q'q"p
p!q'q!p
(p"q)"r' p"(q"r)
(p!q) !r' p!(q!r)
Law
Identity
Domination
Idempotent
Double negation
Negation
Commutative
Associative
14

'
p"(q!r) '(p"q)!(q"r)
p!(q"r) '(p!q)"(q!r)
¬(p"q) ' ¬p!¬q
¬(p!q) ' ¬p"¬q
p"(p!q)'p
p!(p"q)'p
Law
Distributive
DeMorgan
Absorption
All of these laws can be proven concretely using truth tables. It is a good
exercise to see if you can prove some.
15
Well known logical equivalences involving conditional statements:
p%q ' ¬p"q
p%q ' ¬q%¬p
p"q ' ¬p%q
p!q ' ¬(p%¬q)
¬(p%q) ' p!¬q
(p%q)!(p%r) ' p%(q!r)
(p%r)!(q%r) ' (p"q)%r
(p%q)"(p%r) ' p%(q"r)
(p%r)"(q%r) ' (p!q)%r
Well known logical equivalences involving biconditional statements:
p&q ' (p%q)!(q%p)
p&q ' ¬p&¬q
p&q ' (p!q) " (¬p!¬q)
¬(p&q) ' p&¬q
16

Propositional logic is pretty limited. Almost anything you really are interested in
requires a more sophisticated form of logic: predicate logic with quantifiers (or
predicate calculus).
Definition: P(x) is a propositional function when a specific value x is substituted
for the expression in P(x) gives us a proposition. The part of the expression
referring to x is known as the predicate.
Examples:
• P(x): x > 24. P(2) = F, P(102) = T.
• P(x): x = y + 1. P(x) = T for one value only (y is an unbounded variable).
• P(x,y): x = y + 1. P(2,1) = T, P(102,-14) = F.
Definition: A statement of the form P(x 1 ,x 2 ,…,x n ) is the value of the
propositional function P at the n-tuple (x 1 ,x 2 ,…,x n ). P is also known as a n-place
(or n-ary) predicate.
17
Definition: The universal quantification of P(x) is the statement P(x) is true for
all values of x in some domain, denoted by (x P(x).
Definition: The existential quantification of P(x) is the statement P(x) is true for
at least one value of x in some domain, denoted by )x P(x).
Definition: The uniqueness quantification of P(x) is the statement P(x) is true for
exactly one value of x in some domain, denoted by )!x P(x).
There is an infinite number of quantifiers that can be constructed, but the three
above are among the most important and common.
Examples: Assume x belongs to the real numbers.
• (x 0). The negative real numbers form the domain.
• )!x (x 1223 = 0).
18

( and ) have higher precedence than the logical operators.
Example: (x P(x)!Q(x) means ((x P(x))!Q(x).
Definition: When a variable is used in a quantification, it is said to be bound.
Otherwise the variable is free.
Example: )x (x = y + 1).
Definition: Statements involving predicates and quantifiers are logically
equivalent if and only if they have the same truth value independent of which
predicates are substituted and in which domains are used. Notation: S ' T.
DeMorgan’s Laws for Negation:
• ¬)x P(x) ' (x ¬P(x).
• ¬(x P(x) ' )x ¬P(x).
19
Nested quantifiers just means that more than one is in a statement. The order of
quantifiers is important.
Examples: Assume x and y belong to the real numbers.
• (x)y (x + y = 0).
• (x(y (x < 0) ! (y > 0) % xy < 0.
Quantification of two variables:
Statement When True? When False?
(x(y P(x,y) For all x and y, P(x,y)=T. There is a pair of x and y such that
P(x,y)=F.
(x)y P(x,y) For all x there is a y such There is an x such that for all y,
that P(x,y)=T
P(x,y)=F.
)x(y P(x,y) There is an x such that for For all x there is a y such that
)x)y P(x,y)
all y, P(x,y)=T.
There is a pair x and y
such that P(x,y)=T.
P(x,y)=F.
For all x and y, P(x,y)=F.
20

Rules of Inference are used instead of truth tables in many instances. For n
variables, there are 2 n rows in a truth table, which gets out of hand quickly.
Definition: A propositional logic argument is a sequence of propositions. The
last proposition is the conclusion. The earlier ones are the premises. An
argument is valid if the truth of the premises implies the truth of the conclusion.
Definition: A propositional logic argument form is a sequence of compound
propositions involving propositional variables. An argument form is valid if no
matter what particular propositions are substituted for the proposition variables
in its premises, the conclusion remains true if the premises are all true.
Translation: An argument form with premises p 1 , p 2 , …, p n and conclusion q is
valid when (p 1 !p 2 !…!p n ) % q is a tautology.
21
There are eight basic rules of inference.
Rule Tautology Name
p
[p!( p%q)] % q Modus ponens
p%q
*q
¬q
[¬q!(p%q)] % ¬p Modus tollens
p%q
*¬p
p%q
[(p%q)!(q%r)] % (p%r) Hypothetical syllogism
q%r
* p%r
p"q
[(p"q)!¬p] % q Disjunctive syllogism
¬p
*q
p
*p"q
p % (p"q)
Addition
22

Rule Tautology Name
p!q
(p!q) % p
Simplification
*p
p
[(p)!(q)] % (p!q) Conjunction
q
*p!q
p"q
¬p"r
*q"r
[(p"q)!(¬p"r)]% (q"r) Resolution
23
Rules of Inference for Quantified Statements:
Rule of Inference
(x P(x)
*P(c)
P(c) for an arbitrary c
*(x P(x)
(x (P(x) % Q(x))
P(a), where a is a particular element in the domain
*Q(a)
(x (P(x) % Q(x))
¬Q(a), where a is a particular element in the domain
*¬P(a)
)x P(x)
*P(c) for some c
P(c) for some c
*)x P(x)
Name
Universal instantiation
Universal generalization
Universal modus ponens
Universal modus tollens
Existential instantiation
Existential generalization
24

Sets, Functions, Sequences, and Sums
Definition: A set is a collection of unordered elements.
Examples:
• Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
• N = {1, 2, 3, …} and + = N 0 = {0, 1, 2, 3, …} (Slightly different than text)
• Q = {p/q | p,q,Z, q-0}
• R = {reals}
Definition: The cardinality of a set S is denoted |S|. If |S| = n, where n,Z, then
the set S is a finite set. Otherwise it is an infinite set (|S| = .).
Example: The cardinality of of Z, N, N 0 , Q, and R is infinite.
25
Definition: If |S| = |N|, then S is a countable set. Otherwise it is an uncountable
set.
Examples:
• Q is countable.
• R is uncountable.
Definition: Two sets S and T are equal, denoted S = T, if and only if (x(x,S &
x,T).
Examples:
• Let S = {0, 1, 2} and T = {2, 0, 1}. Then S = T. Order does not count.
• Let S = {0, 1, 2} and T = {0, 1, 3}. Then S - T. Only the elements count.
Definition: The empty set is denoted by /. Note that (S(/,S).
26

Definition: A set S is a subset of a set T if (x,S(x,T) and is denoted S0T. S is
a proper subset of T if S0T, but S-T and is denoted S1T.
Example: S = {1, 0} and T = {0, 1, 2}. Then S1T.
Theorem: (S(S0S).
Proof: By definition, (x,S(x,S).
27
Definition: The Power Set of a set S, denoted P(S), is the set of all possible
subsets of S.
Theorem: If |S| = n, then |P(S)| = 2 n .
Example: S = {0, 1}. Then P(S) = {/, {0}, {1}, {0,1}}
Definition: The Cartesian product of n sets A i is defined by ordered elements
from the A i and is denoted A 1 $A 2 $…$A n = {(a 1 ,a 2 ,…a n ) | a i ,A i }.
Example: Let S = {0, 1} and T = {a, b}. Then S$T = {(0,a), (0,b), (1,a), (1,b)}.
Definition: The union of n sets A i is defined by
n
! = A 1 2A 2 2…2A n = {x | )i x,A i }.
i=1 A i
Definition: The intersection of n sets A i is defined by
n
! = A 1 3A 2 3…3A n = {x | (i x,A i
i=1 A i
28

Definition: n sets A i are disjoint if A 1 3A 2 3…3A n = /.
Definition: The complement of set S with respect to T, denoted T4S, is defined
by T4S = {x,T | x6S}. T4S is also called the difference of S and T.
Definitions: The universal set is denoted U. The universal complement of S is
S = U4S.
29
Examples:
• Let S = {1, 0} and T = {0, 1, 2}. Then
o S1T.
o S3T = S.
o S2T = T.
o T4S = {2}.
o Let U = N 0 . S = {2, 3, …}
• Let S = {0, 1} and T = {2, 3}. Then
o S5T.
o S3T = /.
o S2T = {0, 1, 2, 3}.
o T4S = {2, 3}.
o Let U=R. Then S is the set of all reals except the integers 0 and 1, i.e.,
S = {x,R | x-0 ! x-1}.
30

The textbook has a large number of set identities in a table.
Identity
Law(s)
A2/ = A, A3U = A Identity
A2U = U, A3/ = /
Domination
A2A = A, A3A = A
Idempotent
A = A
Complementation
A2B = B2A, A3B = B3A
Commutative
A2(B2C) = (A2B)2C, A3 (B3C) = (A3B) 3C Associative
A3 (B2C) = (A3B) 2 (A3C)
Distributive
A2(B3C) = (A2B) 3 (A2C)
A!B = A"B, A!B = A"B
DeMorgan
A2 (A3B) = A, A3 (A2B) = A
Absorption
A!A = U, A"A = #
Complement
Many of these are simple to prove from very basic laws.
31
Definition: A function f:A%B maps a set A to a set B, denoted f(a) = b for a,A
and b,B, where the mapping (or transformation) is unique.
Definition: If f:A%B, then
• If (b,B )a,A (f(a) = b), then f is a surjective function or onto.
• If A=B and f(a) = f(b) implies a = b, then f is one-to-one (1-1) or injective.
• A function f is a bijection or a one-to-one correspondence if it is 1-1 and
onto.
Definition: Let f:A%B. A is the domain of f. The minimal set B such that
f:A%B is onto is the image of f.
Definitions: Some compound functions include
n
n
• (!
f
i i )(a) = ! f (a) i=1 i . We can substitute + if we expand the summation.
n
n
• (!
f
i=1 i )(a)=! f (a) i=1 i . We can substitute * if we expand the product.
32

Definition: The composition of n functions f i : A i %A i+1 is defined by
(f 1 °f 2 °…°f n )(a) = f 1 (f 2 (…(f n (a)…)),
where a,A 1 .
Definition: If f: A%B, then the inverse of f, denoted f -1 : B%A exists if and only
if (b,B )a,A (f(a) = b ! f -1 (b) = a).
Examples:
• Let A = [0,1] 1 R, B = [0,2] 1 R.
o f(a) = a 2 and g(a) = a+1. Then f+g: A%B and f*g: A%B.
o f(a) = 2*a and g(a) = a-1. Then neither f+g: A%B nor f*g: A%B.
• Let B = A = [0,1] 1 R.
o f(a) = a 2 and g(a) = 1-a. Then f+g: A%A and f*g: A%A. Both
compound functions are bijections.
o f(a) = a 3 and g(a) = a 1/3 . Then g°f(a): A%A is a bijection.
• Let A = [-1, 1] and B=[0, 1]. Then
o f(a) = a 3 and g(a) = {x>0 | x= a 1/3 }. Then g°f(a): A%B is onto.
33
Definition: The graph of a function f is {(a,f(a)) | a,A}.
Example: A = {0, 1, 2, 3, 4, 5} and f(a) = a 2 . Then
(a) graph(f,A)
(b) an approximation to graph(f,[0,5])
34

Definitions: The floor and ceiling functions are defined by
Examples:
• 7x8 = largest integer smaller or equal to x.
• 9x: = smallest integer larger or equal to x.
• 72.998 = 2, 92.99: = 3
• 7-2.998 = -3, 9-2.99: = -2
Definition: A sequence is a function from either N or a subset of N to a set A
whose elements a i are the terms of the sequence.
Definitions: A geometric progression is a sequence of the form {ar i , i=0, 1, …}.
An arithmetic progression is a sequence of the form {a+id, i=0, 1,…}.
Translation: f(a,r,i) = ar i and f(a,d,i) = a + id are the corresponding functions.
35
There are a number of interesting summations that have closed form solutions.
Theorem: If a,r,R, then
"(n+1)a,
if r=1,
n $
! ar i =
i=0
# ar n+1 -a
$
% r-1 , otherwise.
Proof: If r = 1, then we are left summing a n+1 times. Hence, the r = 1 case is
n
trivial. Suppose r - 1. Let S = ! ar i . Then
n
i=0
i=0
rS = r! ar i
Substitution S formula.
n+1
! ar i
Simplifying.
"
#
$
!
i=1
n
i=0
ar i
S+(ar n+1 -a)
( ) Removing n+1 term and adding 0 term.
%
&
' + arn+1 -a
Substituting S for formula
Solve for S in rS = S+(ar n+1 -a) to get the desired formula.
qed
36

Some other common summations with closed form solutions are
Sum
Closed Form Solution
n
i
n(n+1)
! i=1
2
n
! i
i=1
2
n(n+1)(2n+1)
6
n
! i
i=1
3
n 2 (n+1) 2
4
!
! x
i=0
i , |x|

Theorem: If f i (x) is O(g i (x)), for 1;i;n, then
n
i=1
! f i
(x) is O(max{|g 1 (x)|, |g 2 (x)|, …, |g n (x)|}).
Proof: Let g(x) = max{|g 1 (x)|, |g 2 (x)|, …, |g n (x)|} and C i the constants associated
with O(g i (x)). Then
n
i=1
n
i=1
n
i=1
! f i
(x) ; ! C i
g i
(x) ; ! C i
g(x) = |g(x)| ! C i
= C|g(x)|.
Theorem: If f i (x) is O(g i (x)), for 1;i;n, then ! f i
(x) is O( ! g i
(x) ).
Proof: Let g(x) = |g 1 (x)|$|g 2 (x)|$…|g n (x)| and C i the constants associated with
O(g i (x)). Then
n
i=1
n
i=1
n
i=1
! f i
(x) ; ! C i
g i
(x) ; C! g i
(x) .
n
i=1
n
i=1
n
i=1
39
Definition: Let f and g be functions from either Z or R to R. Then f(x) is
=(g(x)) if there are constants C and k such that |f(x)| < C|g(x)| whenever x>k.
Definition: Let f and g be functions from either Z or R to R. Then f(x) is
>(g(x)) if f(x) = O(g(x)) and f(x) = =(g(x)). In this case, we say that f(x) is of
order g(x).
Comment: f(x) = O(g(x)) notation is great in the limit, but does not always
provide the right bounds for all values of x. =, denoted Big Omega, is used to
provide lower bounds. >, denoted Big Theta, is used to provide both lower and
upper bounds.
n
i=0
Example: f(x) = ! a i
x i with a n -0 is of order x n .
40

Notation: Timing, as a function of the number of elements falls into the field of
Complexity.
Complexity Terminology
>(1) Constant
>(log(n)) Logarithmic
>(n)
Linear
>(nlog(n)) nlog(n)
>(n k )
Polynomial
>(n k log(n)) Polylog
>(k n ), where k>1 Exponential
>(n!)
Factorial
Notation: Problems are tractable if they can be solved in polynomial time and
are intractable otherwise.
41
Algorithms, Integers, and Matrices
Definition: An algorithm is a finite set of precise instructions for solving a
problem.
Computational algorithms should have these properties:
• Input: Values from a specified set.
• Output: Results using the input from a specified set.
• Definiteness: The steps in the algorithm are precise.
• Correctness: The output produced from the input is the right solution.
• Finiteness: The results are produced using a finite number of steps.
• Effectiveness: Each step must be performable and in a finite amount of
time.
• Generality: The procedure should accept all input from the input set, not
just special cases.
42

!
Algorithm: Find the maximum value of " a i
! $
procedure max( " a
# i
% : integers)
&i=1
max := a 1
for i := 2 to n
if max < a i then max := a i
{max is the largest element}
n
#
n
$
%
&i=1
, where n is finite.
Proof of correctness: We use induction.
1. Suppose n = 1, then max := a 1 , which is the correct result.
2. Suppose the result is true for k = 1, 2, …, i-1. Then at step i, we know that
max is the largest element in a 1 , a 2 , …, a i-1 . In the if statement, either max is
already larger than a i or it is set to a i . Hence, max is the largest element in
a 1 , a 2 , …, a i . Since i was arbitrary, we are done. qed
This algorithm’s input and output are well defined and the overall algorithm can
be performed in O(n) time since n is finite. There are no restrictions on the input
set other than the elements are integers.
43
!
Algorithm: Find a value in a sorted, distinct valued " a
# i
There are many, many search algorithms.
! $
procedure linear_search(x, " a
# i
% : integers)
&i=1
i := 1
while (i;n and x-a i )
i := i + 1
if i;n then location := i else location := 0
!
{location is the subscript of " a
# i
n
n
$
%
&i=1
n
$
%
&i=1
, where n is finite.
!
equal to x or 0 if x is not in " a
# i
n
$
% }
&i=1
We can prove that this algorithm is correct using an induction argument. This
algorithm does not rely on either distinctiveness nor sorted elements.
Linear search works, but it is very slow in comparison to many other searching
algorithms. It takes 2n+2 comparisons in the worst case, i.e., O(n) time.
44

! $
procedure binary_search(x, " a
# i
% : integers)
&i=1
i := 1
j := n
while ( i < j )
m := 7(i+j)/28
if x > a m then i := m+1 else j := m
if x = a i then location := i else location := 0
!
{location is the subscript of " a
# i
n
n
$
%
&i=1
!
equal to x or 0 if x is not in " a
# i
We can prove that this algorithm is correct using an induction argument.
n
$
% }
&i=1
This algorithm is much, much faster than linear_search on average. It is O(logn)
!
in time. The average time to find a member of " a
# i
order n.
n
$
%
&i=1
can be proven to be of
45
!
Algorithm: Sort the distinct valued " a
# i
finite.
n
$
%
&i=1
into increasing order, where n is
There are many, many sorting algorithms.
! $
procedure bubble_sort( " a
# i
% : reals, n>1)
&i=1
for i := 1 to n-1
for j := 1 to n-i
if a j > a j+1 then swap a j and a j+1
!
{ " a
# i
n
$
%
&i=1
is in increasing order}
n
This is one of the simplest sorting algorithms. It is expensive, however, but quite
easy to understand and implement. Only one temporary is needed for the
swapping and two loop variables as extra storage. The worst case time is O(n 2 ).
46

!
procedure insertion_sort( " a
# i
for j := 2 to n
i := 1
while a j > a i
i := i + 1
t := a j
for k := 0 to j-i-1
a j-k := a j-k-1
a i := t
!
{ " a
# i
n
$
%
&i=1
n
$
%
&i=1
is in increasing order}
: reals, n>1)
This is not a very efficient sorting algorithm either. However, it is easy to see
that at the j th step that the j th element is put into the correct spot. The worst case
time is O(n 2 ). In fact, insertion_sort is trivially slower than bubble_sort.
47
Number theory is a rich field of mathematics. We will study four aspects briefly:
1. Integers and division
2. Primes and greatest common denominators
3. Integers and algorithms
4. Applications of number theory
Most of the theorems quoted in this part of the textbook require knowledge of
mathematical induction to rigorously prove, a topic covered in detail in the next
chapter. !
48

Definition: If a,b,Z and a-0, we say that a divides b if )c,Z(b=ac), denoted by
a | b. When a divides b, we denote a as a factor of b and b as a multiple of a.
When a does not divide b, we denote this as a/|b.
Theorem: Let a,b,c,Z. Then
1. If a | b and a | c, then a | (b+c).
2. If a | b, then a | (bc).
3. If a | b and b | c, then a | c.
Proof: Since a | b, )s,Z(b=as).
1. Since a | c it follows that ) t,Z(c=at). Hence, b+c = as + at = a(s+t).
Therefore, a | (b+c).
2. bc = (as)c = a(sc). Therefore, a | (bc).
3. Since b | c it follows that ) t,Z(c=bt). c = bt = (as)t = a(st), Therefore, a | c.
Corollary: Let a,b,c,Z. If a | b and b | c, then a | (mb+nc) for all m,n,Z.
49
Theorem (Division Algorithm): Let a,d,Z(d > 0). Then )!q,r,Z(a = dq+r).
Definition: In the division algorithm, a is the dividend, d is the divisor, q is the
quotient, and r is the remainder. We write q = a div d and r = a mod d.
Examples:
• Consider 101 divided by 9: 101 = 11$9 + 2.
• Consider -11 divided by 3: -11 = 3(-4) + 1.
Definition: Let a,b,m,Z(m > 0). Then a is congruent to b modulo m if m | (a-b),
denoted a ' b (mod m). The set of integers congruent to an integer a modulo m
is called the congruence class of a modulo m.
Theorem: Let a,b,m,Z(m > 0). Then a ' b (mod m) if and only if a mod m = b
mod m.
50

Examples:
• Does 17 ' 5 mod 6? Yes, since 17 – 5 = 12 and 6 | 12.
• Does 24 ' 14 mod 6? No, since 24 – 14 = 10, which is not divisible by 6.
Theorem: Let a,b,m,Z(m > 0). Then a ' b (mod m) if and only if
)k,Z(a=b+km).
Proof: If a ' b (mod m), then m | (a-b). So, there is a k such that a-b = km, or a =
b+km. Conversely, if there is a k such that a = b + km, then km = a-b. Hence, m
| (a-b), or a ' b (mod m).
Theorem: Let a,b,c,d,m,Z(m > 0). If a ' b (mod m) and c ' d (mod m), then
a+c ' b+d (mod m) and ac ' bd (mod m).
Corollary: Let a,b,m,Z(m > 0). Then (a+b) mod m = ((a mod m)+(b mod m))
mod m and (ab) mod m = ((a mod m)(b mod m)) mod m.
51
Some applications involving congruence include
• Hashing functions h(k) = k mod m.
• Pseudorandom numbers: x n+1 = (ax n +c) mod m.
o c = 0 is known as a pure multiplicative generator.
o c - 0 is known as a linear congruential generator.
• Cryptography
Definition: A positive integer a is a prime if it is divisible only by 1 and a. It is a
composite otherwise.
Fundamental Theorem of Arithmetic: Every positive integer greater than 1 can
be written uniquely as a prime or the product of two or more primes where the
prime factors are written in nondecreasing order.
Theorem: If a is a composite number, then a has a prime divisor less than or
equal to a 1/2 .
52

Theorem: There are infinitely many primes.
Prime Number Theorem: The ratio of primes not exceeding a and x/ln(a)
approaches 1 as a%..
Example: The odds of a randomly chosen positive integer n being prime is given
by (n/ln(n))/n = 1/ln(n) asymptotically.
There are still a number of open questions regarding the distribution of primes.
Definition: Let a,b,Z(a and b not both 0). The largest integer d such that d | a
and d | b is the greatest common devisor of a and b, denoted by gcd(a,b).
Example: gcd(24,36) = 12.
Definition: The integers a and b are relatively prime if gcd(a,b) = 1.
53
!
Definition: The integers " a
# i
whenever 1;i

Integers can be expressed uniquely in any base.
Theorem: Let b,Z(b>1). Then if n,N, then there is a unique expression such
that n = a k b k + a k-1 b k-1 +…+a 1 b+a 0 , where {a i },k,N 0 , a k -0, and 0;a i 1, is really easy. Just group k bits together and
convert to the base 2 k symbol.
• Base 10 to any base 2 k is a pain.
• Base 2 k to base 10 is also a pain.
56

Algorithm: Addition of integers
procedure add(a, b: integers)
(a n-1 a n-2 …a 1 a 0 ) 2 := base_2_expansion(a)
(b n-1 b n-2 …b 1 b 0 ) 2 := base_2_expansion(b)
c := 0
for j := 0 to n-1
d := 7(a j +b j +c)/28
s j := a j +b j +c – 2d
c := d
s n := c
{the binary expansion of the sum is (s k-1 s k-2 …s 1 s 0 ) 2 }
Questions:
• What is the complexity of this algorithm?
• Is this the fastest way to compute the sum?
57
Algorithm: Mutiplication of integers
procedure multiply(a, b: integers)
(a n-1 a n-2 …a 1 a 0 ) 2 := base_2_expansion(a)
(b n-1 b n-2 …b 1 b 0 ) 2 := base_2_expansion(b)
for j := 0 to n-1
if b j = 1 then c j := a shifted j places else c j := 0
{c 0 ,c 1 ,…,c n-1 are the partial products}
p := 0
for j := 0 to n-1
p := p + c j
{p is the value of ab}
Examples:
• (10) 2 $(11) 2 = (110) 2 . Note that there are more bits than the original integers.
• (11) 2 $(11) 2 = (1001) 2 . Twice as many binary digits!
58

Algorithm: Compute div and mod
procedure division(a: integer, d: positive integer)
q := 0
r := |a|
while r < d
r := r – d
q := q + 1
if a < 0 and r > 0 then
r := d – r
q := -(q + 1)
{q = a div d is the quotient and r = a mod d is the remainder}
Notes:
• The complexity of the multiplication algorithm is O(n 2 ). Much more
efficient algorithms exist, including one that is O(n 1.585 ) using a divide and
conquer technique we will see later in the course.
• There are O(log(a)log(d)) complexity algorithms for division.
59
Modular exponentiation, b k mod m, where b, k, and m are large integers is
important to compute efficiently to the field of cryptology.
Algorithm: Modular exponentiation
procedure modular_exponentiation(b: integer, k,m: positive integers)
(a n-1 a n-2 …a 1 a 0 ) 2 := base_2_expansion(k)
y := 1
power := b mod m
for i := 0 to n-1
if a i = 1 then y := (y $ power) mod m
power := (power $ power) mod m
{y = b k mod m}
Note: The complexity is O((log(m)) 2 log(k)) bit operations, which is fast.
60

Euclidean Algorithm: Compute gcd(a,b)
procedure gcd(a,b: positive integers)
x := a
y := b
while y-0
r := x mod y
x := y
y := r
{gcd(a,b) is x}
Correctness of this algorithm is based on
Lemma: Let a=bq+r, where a,b,q,r,Z. then gcd(a,b) = gcd(b,r).
The complexity will be studied after we master mathematical induction.
61
Number theory useful results
Theorem: If a,b,N then )s,t,Z(gcd(a,b) = sa+tb).
Lemma: If a,b,c,N (gcd(a,b) = 1 and a | bc, then a | c).
Note: This lemma makes proving the prime factorization theorem doable.
Lemma: If p is a prime and p | a 1 a 2 …a n where each a i ,Z, then p | a i for some i.
Theorem: Let m,N and let a,b,c,Z. If ac ' bc (mod m) and gcd(c,m) = 1, then
a ' b (mod m).
Definition: A linear congruence is a congruence of the form ax ' b (mod m),
where m,N, a,b,Z, and x is a variable.
Definition: An inverse of a modulo m is an a such that aa ' 1 (mod m).
62

Theorem: If a and m are relatively prime integers and m>1, then an inverse of a
modulo m exists and is unique modulo m.
Proof: Since gcd(a,m) = 1, )s,t,Z(1 = sa+tb). Hence, sa=tb ' 1 (mod m). Since
tm ' 0 (mod m), it follows that sa ' 1 (mod m). Thus, s is the inverse of a
modulo m. The uniqueness argument is made by assuming there are two
inverses and proving this is a contradiction.
Systems of linear congruences are used in large integer arithmetic. The basis for
the arithmetic goes back to China 1700 years ago.
Puzzle Sun Tzu (or Sun Zi): There are certain things whose number is unknown.
• When divided by 3, the remainder is 2.
• When divided by 5, the remainder is 3, and
• When divided by 7, the remainder is 2.
What will be the number of things? (Answer: 23… stay tuned why).
63
Chinese Remander Theorem: Let m 1 , m 2 ,…,m n ,N be pairwise relatively prime.
n
Then the system x ' a i (mod m i ) has a unique solution modulo m = ! .
i=1
m i
Existence Proof: The proof is by construction. Let M k = m / m k , 1;k;n. Then
gcd(M k , m k ) = 1 (from pairwise relatively prime condition). By the previous
theorem we know that there is a y k which is an inverse of M k modulo m k , i.e.,
M k y k ' 1 (mod m k ). To construct the solution, form the sum
x = a 1 M 1 y 1 + a 2 M 2 y 2 + … + a n M n y n .
Note that M j ' 0 (mod m k ) whenever j-k. Hence,
x ' a k M k y k ' a k (mod m k ), 1;k;n.
We have shown that x is simultaneous solution to the n congruences. qed
64

Sun Tzu’s Puzzle: The a k ,{2, 1, 2} from 2 pages earlier. Next
The inverses y k are
m k ,{3, 5, 7}, m=3$5$7=105, and M k =m/m k ,{35, 21, 15}.
1. y 1 = 2 (M 1 = 35 modulo 3).
2. y 2 = 1 (M 2 = 21 modulo 5).
3. y 3 = 1 (M 3 = 15 modulo 7).
The solutions to this system are those x such that
x ' a 1 M 1 y 1 + a 2 M 2 y 2 + a 2 M 2 y 2 = 2$35$2 + 3$21$1 + 2$15$1 = 233
Finally, 233 ' 23 (mod 105).
65
Definition: A m$n matrix is a rectangular array of numbers with m rows and n
columns. The elements of a matrix A are noted by A ij or a ij . A matrix with m=n
is a square matrix. If two matrices A and B have the same number of rows and
columns and all of the elements A ij = B ij , then A = B.
Definition: The transpose of a m$n matrix A = [A ij ], denoted A T , is A T = [A ji ]. A
matrix is symmetric if A = A T and skew symmetric if A = -A T .
Definition: The i th row of an m$n matrix A is [A i1 , A i2 , …, A in ]. The j th column
is [A 1j , A 2j , …, A mj ] T .
Definition: Matrix arithmetic is not exactly the same as scalar arithmetic:
• C = A + B: c ij = a ij + b ij , where A and B are m$n.
• C = A – B: c ij = a ij - b ij , where A and B are m$n
k
• C = AB: c ij
= ! a ip
b pj
, where A is m$k, B is k$n, and C is m$n.
p=1
66

Theorem: A±B = B±A, but AB-BA in general.
Definition: The identity matrix I n is n$n with I ii = 1 and I ij = 0 if i-j.
Theorem: If A is n$n, then AI n = I n A = A.
Definition: A r = AA … A (r times).
Definition: Zero-One matrices are matrices A = [a ij ] such that all a ij ,{0, 1}.
Boolean operations are defined on m$n zero-one matrices A = [a ij ] and B = [b ij ]
by
• Meet of A and B: A!B = a ij !b ij , 1;i;m and 1;j;n.
• Join of A and B: A"B = a ij "b ij , 1;i;m and 1;j;n.
• The Boolean product of A and B is C = A !B, where A is m$k, B is k$n,
and C is m$n, is defined by c ij = (a i1 !b 1j )"(a i2 !b 2j )"…"(a ik !b kj ).
Definition: The Boolean power of a n$n matrix A is defined by A [r] =
A !A !… !A (r times), where A [0] = I n .
67
Induction and Recursion
Principle of Mathematical Induction: Given a propositional function P(n), n,N,
we prove that P(n) is true for all n,N by verifying
1. (Basis) P(1) is true
2. (Induction) P(k)%P(k+1), (k,N.
Notes:
• Equivalent to [P(1) ! (k,N (P(k)%P(k+1))] % (n,N P(n).
• We do not actually assume P(k) is true. It is shown that if it is assumed that
P(k) is true, then P(k+1) is also true. This is a subtle grammatical point with
mathematical implications.
• Mathematical induction is a form of deductive reasoning, not inductive
reasoning. The latter tries to make conclusions based on observations and
rules that may lead to false conclusions.
• Sometimes P(1) is not the basis, but some other P(k), k,Z.
68

• Sometimes P(k) is for a (possibly infinite) subset of N or Z.
• Sometimes P(k-1)%P(k) is easier to prove than P(k)%P(k+1).
• Being flexible, but staying within the guiding principle usually works.
• There are many ways of proving false results using subtly wrong induction
arguments. Usually there is a disconnect between the basis and induction
parts of the proof.
• Examples 10, 11, and 12 in your textbook are worth studying until you
really understand each.
n
Lemma: ! (2i-1) = n
i=1
2 (sum of odd numbers).
Proof: (Basis) Take k = 1, so 1 = 1.
(Induction) Assume 1+3+5+…+(2k-1) = k 2 for an arbitrary k > 1. Add 2k+1 to
both sides. Then (1+3+5+…+(2k-1))+(2k+1) = k 2 +(2k+1) = (k+1) 2 .
69
n
i=0
Lemma: ! 2 i = 2 n+1 -1.
Proof: (Basis) Take k=0, so 2 0 = 1 = 2 1 – 1.
k
(Induction) Assume ! 2
i=0
i = 2 k+1 -1 for an arbitrary k > 0. Add 2 k+1 to both
sides. Then
k
! 2
i=0
i + 2 k+1 = 2 k+1 -1 + 2 k+1 ,
which simplifies to
k+1
2
i=0
i
! = 2 k+2 -1.
Principle of Strong Induction: Given a propositional function P(n), n,N, we
prove that P(n) is true for all n,N by verifying
1. (Basis) P(1) is true
2. (Induction) [P(1)!P(2)!…!P(k)]%P(k+1) is true (k,N.
70

Example: Infinite ladder with reachable rungs. For mathematical or strong
induction, we need to verify the following:
Step Mathematical Strong
Basis
We can reach the first rung.
Induction If we can reach an arbitrary (k,N, if we can reach all k
rung k, then we can reach rungs, then we can reach
rung k+1.
rung k+1.
We cannot prove that you can climb an infinite ladder using mathematical
induction. Using strong induction, however, you can prove this result using a
trick: since you can prove that you can climb to rungs 1, 2, …, k, it follows that
you can climb 2 rungs arbitrarily, which gets you from rung k-1 to rung k+1.
Rule of thumb: Always use mathematical induction if P(k)%P(k+1) % (k,N.
Only resort to strong induction when that fails.
71
Fundamental Theorem of Arithmetic: Every n,N (n>1) is the product of primes.
Proof: Let P(n) be the proposition that n can be written as the product of primes.
(Basis) P(2) is true: 2 = 2, the product of 1 prime.
(Induction) Assume P(j) is true (j;k. We must verify that P(k+1) is true.
Case 1: k+1 is a prime. Hence, P(k+1) is true.
Case 2: k+1 is a composite. Hence k+1 = a•b, where 2;a;b

Example: Every postage amount < $.12 can be formed using $.04 and $.05
stamp combinations only. We can prove this using modified strong induction.
(Basis) Consider 4 specific cases:
Postage Number of $.04’s Number of $.05’s
$.12 3 0
$.13 2 1
$.14 1 2
$.15 0 3
Hence, P(j) is true for 12;j;15.
(Induction) Assume P(j) is true for 12;j;k and k2.
• h(0) = 1, h(n) = nh(n-1) = n!
• Fibonacci numbers: f 0 = 0, f 1 = 1, f n = f n-1 + f n-2 , n>1.
n 0 1 2 3 4
f(n) 1 6 16 36 76
g(n) 12 1 -10 -21 -32
h(n) 1 1 2 6 24
f n 0 1 1 2 3
74

Theorem: Whenever n ? n-2 , where !=(1+ 5)/2 .
The proof is by modified strong induction.
Lamé’s Theorem: Let a,b,N (a

Definition: A recursive algorithm solves a problem by reducing it to an instance
of the same problem with smaller input(s).
Note: Recursive algorithms can be proven correct using mathematical induction
or modified strong induction.
Examples:
• n! = n•(n-1)!
• a n = a•(a n-1 )
• gcd(a,b) with a,b,N (a

• Fibonacci numbers
procedure fib(n: n,N 0 )
if n = 0 then fib(0) := 0
else if n = 1 then fib(1) := 1
else fib(n) := fib(n-1) + fib(n-2)
or it can be defined iteratively:
procedure fib(n: n,N 0 )
if n = 0 then y := 0
else
x := 0, y := 1
for I := 1 to n-1
z := x+y
x := y
y := z
{y is f n }
79
Graphs and trees are important concepts that we will spend a lot of time
considering later in the course.
• A graph is made up of vertices and edges that connect some of the vertices.
• A tree is a special form of a graph, namely it is a connected unidirectional
graph with no simple circuits.
• A rooted tree is a tree with one vertex that is the root and every edge is
directed away from the root.
• A m-ary tree is a rooted tree such that every internal vertex has no more
than m children. If m = 2, it is a binary tree.
• The height of a rooted tree T, denoted h(T), is the maximum number of
levels (or vertices).
• A balanced rooted tree T has all of its leaves at h(T) or h(T)-1.
Let T 1 , T 2 , …, T m be rooted trees with roots r 1 , r 2 , …, r m . Let r be another root.
Connecting r to the roots r 1 , r 2 , …, r m constructs another rooted tree T. We can
reformulate this concept using the recursive set methodology.
80

Merge sort is a balanced binary tree method that first breaks a list up recursively
into two lists until each sublist has only one element. Then the sublists are
recombined, two at a time and sorted order, until only one sorted list remains.
Note: The height of the tree formed in merge sort is O(log 2 n) for n elements.
Notes:
10, 4, 7, 1
10, 4 7, 1
10 4 7 1
4, 10 1, 7
1, 4, 7, 10
• First three rows do the sublist splitting.
• Last two rows do the merging.
• There are two distinct algorithms at work.
81
!
procedure merge_sort(L = " a
# i
if n > 1 then
m := 7n/28
!
L 1 := " a i
m
$
%
# &i=1
n
$
%
&i=m+1
n
$
% )
&i=1
!
L 2 := " a
# i
L := merge(merge_sort(L 1 ), merge_sort(L 2 ))
!
{L is now the sorted " a
# i
n
$
% }
&i=1
procedure merge(L 1 , L 2 : sorted lists)
L := /
while L 1 and L 2 are both nonempty
remove the smaller of the first element of L 1 and L 2 and append it to
end of L
if either L 1 or L 2 are empty, append the other list to the end of L
{L is the merged, sorted list}
82

Theorem: If n i = |L i |, i=1,2, then merge requires at most n 1 +n 2 -1 comparisons. If
n = |L|, then merge_sort requires O(nlog 2 n) comparisons.
Quick sort is another sorting algorithm that breaks an initial list into many
! $
sublists, but using a different heuristic than merge sort. If L = " a
# i
% with
&i=1
distinct elements, then quick sort recursively constructs two lists: L 1 for all a i <
a 1 and L 2 for all a i > a 1 with a 1 appended to the end of L 1 . This continues
recursively until each sublist has only one element. Then the sublists are
recombined in order to get a sorted list.
Note: On average, the number of comparisons is O(nlog 2 n) for n elements, but
can be O(n 2 ) in the worst case. Quick sort is one of the most popular sorting
algorithms used in academia.
Exercise: Google “quick sort, C++” to see many implementations or look in
many of the 200+ C++ primers. Defining quick sort is in Rosen’s exercises.
n
83
Counting, Permutations, and Combinations
Product Rule Principle: Suppose a procedure can be broken down into a
sequence of k tasks. If there are n i , 1;i;k, ways to do the i th task, then there are
!
k
i=1
n i
ways to do the procedure.
Sum Rule Principle: Suppose a procedure can be broken down into a sequence
of k tasks. If there are n i , 1;i;k, ways to do the i th task, with each way unique,
k
then there are ! ways to do the procedure.
i=1
n i
Exclusion (Inclusion) Principle: If the sum rule cannot be applied because the
ways are not unique, we use the sum rule and subtract the number of duplicate
ways.
Note: Mapping the individual ways onto a rooted tree and counting the leaves is
another method for summing. The trees are not unique, however.
84

Examples:
• Consider 3 students in a classroom with 10 seats. There are 10$9$8 = 720
ways to assign the students to the seats.
• We want to appoint 1 person to fill out many, may forms that the
administration wants filled in by today. There are 3 students and 2 faculty
members who can fill out the forms. There are 3+2 = 5 ways to choose 1
person. (Duck fast.)
• How many variables are legal in the orginal Dartmouth BASIC computer
language? Variables are 1 or 2 alphanumeric characters long, begin with A-
Z, case independent, and are not one of the 5 two character reserved words
in BASIC. We use a combination of the three counting principles:
o 1 character variables: V 1 = 26
o 2 character variables: V 2 = 26$36 - 5 = 931
o Total: V = V 1 + V 2 = 957
85
Pigeonhole Principle: If there are k,N boxes and at least k+1 objects placed in
the boxes, then there is at least one box with more than one object in it.
Theorem: A function f: D%E such that |D| >k and |E| = k, then f is not 1-1.
The proof is by the pigeonhole principle.
Theorem (Generalized Pigeonhole Principle): If N objects are placed in k boxes,
then at least one box contains at least 9N/k: - 1 objects.
Proof: First recall that 9N/k: < (N/k)+1. Now suppose that none of the boxes
contains more than 9N/k: - 1 objects. Hence, the total number of objects has to
be
k(9N/k: - 1) < k((N/k)+1)-1) = N. %B
Hence, the theorem must be true (proof by contradiction).
Theorem: Every sequence of n 2 +1 distinct real numbers contains a subsequence
of length n+1 that is either strictly increasing or decreasing.
86

Examples: From a standard 52 card playing deck.
• How many cards must be dealt to guarantee that k = 4 cards from the same
suit are dealt?
o GPP Theorem says 9N/k: - 1 < 4 or N = 17.
o Real minimum turns out to be 9N/k: < 4 or N = 16.
• How many cards must be dealt to guarantee that 4 clubs are dealt?
o GPP Theorem does not apply.
o The product rule and inclusion principles apply: 3$13+4 = 43 since all
of the hearts, spaces, and diamonds could be dealt before any clubs.
Definition: A permutation of a set of distinct objects is an ordered arrangment of
these objects. A r-permutation is an ordered arrangement of r of these objects.
Example: Given S = {0,1,2}, then {2,1,0} is a permutation and {0,2} is a 2-
permutation of S.
87
Theorem: If n,r,N, then there are P(n,r) = n$(n-1)$(n-2)$…$(n-r+1) = n!/(n-r)!
r-permutations of a set of n distinct elements. Further, P(n,0) = 1.
The proof is by the product rule for r

Theorem: The number of r-combinations of a set with n elements with n,r,N 0 is
C(n,r) = n # r
!
"
$
.
%
&
Proof: The r-permutations can be formed using C(n,r) r-combinations and then
ordering each r-combination, which can be done in P(r,r) ways. So,
P(n,r) = C(n,r)$P(r,r)
or
C(n,r) = P(r,r)
P(n,r) = n!
(n-r)! !(r-r)! = n!
r! r!(n-r)! .
Theorem: C(n,r) = C(n,n-r) for 0;r;n.
Definition: A combinatorial proof of an identity is a proof that uses counting
arguments to prove that both sides f the identity count the same objects, but in
different ways.
89
Binomial Theorem: Let x and y be variables. Then for n,N,
(x+y) n n ! n$
= # &
' x
j=0#
j
n-j y j .
&
Proof: Expanding the terms in the product all are of the form x n-j y j for
j=0,1,…,n. To count the number of terms for x n-j y j , note that we have to choose
n-j x’s from the n sums so that the other j terms in the product are y’s. Hence,
the coefficient for x n-j y j ! n $
is # &
# n-j
= ! n $
# &
& # j
.
&
"
%
"
%
Example: What is the coefficient of x 12 y 13 in (x+y) 25 !
? 25 $
# &
#
13
= 5,200,300.
&
n ! n$
Corollary: Let n,N 0 . Then # &
' k=0#
k
= 2n .
&
Proof: 2 n = (1+1) n n ! n$
= # &
# k
1k 1 n-k n ! n$
= # &
'
&
' .
k=0
k=0#
k&
"
%
"
%
"
"
%
%
"
%
90

n
k=0
Corollary: Let n,N 0 . Then (-1) k n # &
'
# k
= 0 .
&
Proof: 0 = 0 n = ((-1)+1) n n ! n$
= # &
# k
(-1)k 1 n-k n
= (-1) k ! n $
# &
'
&
' .
k=0
k=0 # k&
!
Corollary: n # &
# 0
+ n # &
& # 2
+ n # &
& # 4
+!= n # &
& # 1
+ n # &
& # 3
+ n # &
& # 5
+!
&
"
$
%
!
"
$
%
!
"
$
%
Corollary: Let n,N 0 . Then 2 k n # &
'
# k
= 3n .
&
!
"
$
%
!
"
n
k=0
!
Theorem (Pascal’s Identity): Let n,k,N with n

If we allow repetitions in the permutations, then all of the previous theorems and
corollaries no longer apply. We have to start over !.
Theorem: The number of r-permutations of a set with n objects and repetition is
n r .
Proof: There are n ways to select an element of the set of all r positions in the r-
permutation. Using the product principle completes the proof.
Theorem: There are C(n+r-1,r) = C(n+r-1,n-1) r-combinations from a set with n
elements when repetition is allowed.
Example: How many solutions are there to x 1 +x 2 +x 3 = 9 for x i ,N? C(3+9-1,9) =
C(11,9) = C(11,2) = 55. Only when the constraints are placed on the x i can we
possibly find a unique solution.
Definition: The multinomial coefficient is C(n; n 1 , n 2 , …, n k ) = n!
k
! n i
!
.
i=1
93
Theorem: The number of different permutations of n objects, where there are n i ,
1;i;k, indistinguishable objects of type i, is C(n; n 1 , n 2 , …, n k ).
Theorem: The number of ways to distribute n distinguishable objects in k
distinguishable boxes so that n i objects are placed into box i, 1;i;k, is C(n; n 1 ,
n 2 , …, n k ).
Theorem: The number of ways to distribute n distinguishable objects in k
indistinguishable boxes so that n i objects are placed into box i, 1;i;k, is
k
j=11
j!
Multinomial Theorem: If n,N, then
"
$
$
#
!
k
i=1
x i
n
%
'
'
&
j-1
j"
%
j
" %
! -1 $ ' "
! #
$
&
' j-i
i=0 $
i'
#
$
#
&
%
& 'n
.
n
= ! n1
C(n;n 1
,n 2
,...,n
+n 2
+...n k
)x 1
n
k
=k
1
x 2
n
2
...x k k
.
94

Generating permutations and combinations is useful and sometimes important.
Note: We can place any n-set into a 1-1 correspondence with the first n natural
numbers. All permutations can be listed using {1, 2, …, n} instead of the actual
set elements. There are n! possible permutations.
Definition: In the lexicographic (or dictionary) ordering, the permutation of
{1,2,…,n} a 1 a 2 …a n precedes b 1 b 2 …b n if and only if a i ; b i , for all 1;i;n.
Examples:
• 5 elements. The permutation 21435 precedes 21543.
• Given 362541, then 364125 is the next permutation lexicographically.
95
Algorithm: Generate the next permutation in lexicographic order.
procedure next_perm(a 1 a 2 …a n : a i ,{1,2,…,n} and distinct)
j := n – 1
while a j > a j+1
j := j – 1
{j is the largest subscript with a j < a j+1 }
k := n
while a j > a k
k := k – 1
{a k is the smallest integer greater than a j to the right of a j }
Swap a j and a k
r := n, s := j+1
while r > s
Swap a r and a s
r := r – 1, s:= s + 1
{This puts the tail end of the permutation after the j th
increasing order}
position in
96

Algorithm: Generating the next r-combination in lexicographic order.
procedure next_r_combination(a 1 a 2 …a n : a i ,{1,2,…,n} and distinct)
i := r
while a i = n-r+1
i := i – 1
a i := a i + 1
for j := i+1 to r
a j := a i + j - 1
Example: Let S = {1, 2, …, 6}. Given a 4-permutation of {1, 2, 5, 6}, the next 4-
permutation is {1, 3, 4, 5}.
97
Discrete Probability
Definition: An experiment is a procedure that yields one of a given set of
possible outcomes.
Definition: The sample space of the experiment is the set of (all) possible
outcomes.
Definition: An event is a subset of the sample space.
First Assumption: We begin by only considering finitely many possible
outcomes.
Definition: If S is a finite sample space of equally likely outcomes and E0S is
an event, then the probability of E is p(E) = |E| / |S|.
98

Examples:
• I randomly chose an exam1 to grade. What is the probability that it is one of
the Davids? Thirty one students took exam1 of which five were Davids. So,
p(David) = 5 / 31 ~ 0.16.
• Suppose you are allowed to choose 6 numbers from the first 50 natural
numbers. The probability of picking the correct 6 numbers in a lottery
drawing is 1/C(50,6) = (44!$6!) / 50! ~ 1.43$10 -9 . This lottery is just a
regressive tax designed for suckers and starry eyed dreamers.
Definition: When sampling, there are two possible methods: with and without
replacement. In the former, the full sample space is always available. In the
latter, the sample space shrinks with each sampling.
99
Example: Let S = {1, 2, …, 50}. What is the probability of sampling {1, 14, 23,
32, 49}?
• Without replacement: p({1,14,23,32,49}) = 1 / (50$49$48$47$46) =
3.93$10 -9 .
• With replacement: p({1,14,23,32,49}) = 1 / (50$50$50$50$50) = 3.20$10 -9 .
Definition: If E is an even, then E is the complementary event.
Theorem: p(E) = 1 – p(E) for a sample space S.
Proof: p(E) = (|S| – |E|) / |S| = 1 – |E| / |S| = 1 – p(E).
Example: Suppose we generate n random bits. What is the probability that one
of the bits is 0? Let E be the event that a bit string has at least one 0 bit. Then E
is the event that all n bits are 1. p(E) = 1 – p(E) = 1 – 2 -n = (2 n – 1) / 2 n .
Note: Proving the example directly for p(E) is extremely difficult.
100

Theorem: Let E and F be events in a sample space S. Then
p(E2F) = p(E) + p(F) – p(E3F).
Proof: Recall that |E2F| = |E| + |F| – |E3F|. Hence,
p(E2F) = |E2F| / |S| = (|E| + |F| – |E3F|) / |S| = p(E) + p(F) – p(E3F).
Example: What is the probability in the set {1, 2, …, 100} of an element being
divisible by 2 or 3? Let E and F represent elements divisible by 2 and 3,
respectively. Then |E| = 50, |F| = 33, and |E3F| = 16. Hence, p(E2F) = 0.67.
101
Second Assumption: Now suppose that the probability of an event is not 1 / |S|.
In this case we must assign probabilities for each possible event, either by
setting a specific value or defining a function.
Definition: For a sample space S with a finite or countable number of events, we
assign probabilities p(s) to each event s,S such that
(1) 0 ; p(s) ; 1 (s,S, and
(2) " p(s) = 1.
s!S
Notes:
1. When |S| = n, the formulas (1) and (2) can be rewritten using n.
2. When |S| = . and is uncountable, integral calculus is required for (2).
3. When |S| = . and is countable, the sum in (2) is true in the limit.
102

Example: Coin flipping with events H and T.
• S = {H, T} for a fair coin. Hence, p(H) = p(T) = 0.5.
• S = {H, H, T} for a weighted coin. Then p(H) = 0.67 and p(T) = 0.33.
Definition: Suppose that S is a set with n elements. The uniform distribution
assigns the probability 1/n to each element in S.
Definition: The probability of the event E is the sum of the probabilities of the
outcomes in E, i.e., p(E) = " p(s) .
s!E
Note: When |E| = ., the sum
" p(s) must be convergent in the limit.
s!E
Definition: The experiment of selecting an element from a sample space S with
a uniform distribution is known as selecting an element from S at random.
We can prove that (1) p(E) = 1 – p(E) and (2) p(E2F) = p(E) + p(F) – p(E3F)
using the more general probability definitions.
103
Definition: Let E and F be events with p(F) > 0. The conditional probability of E
given F is defined by p(E|F) = p(E3F) / p(F).
Example: A bit string of length 3 is generated at random. What is the probability
that there are two 0 bits in a row given that the first bit is 0? Let F be the event
that the first bit is 0. Let E be the event that there are two 0 bits in a row. Note
that E3F = {000, 001} and p(F) = 0.5. Hence, p(E|F) = 0.25 / 0.5 = 0.5.
Definition: The events E and F are independent if p(E3F) = p(E)p(F).
Note: Independence is equivalent to having p(E|F) = p(E).
Example: Suppose E is the event that a bit string begins with a 1 and F is the
event that there is are an even number of 1’s. Suppose the bit strings are of
length 3. There are 4 bit strings beginning with 1: {100, 101, 110, 111}. There
are 3 strings with an even number of 1’s: {101, 110, 011}. Hence, p(E) = 0.5
and p(F) = 0.375. E3F = {101, 110}, so p(E3F) = 0.25. Thus, p(E3F) -
p(E)p(F). Hence, E and F are not independent.
104

Note: For bit strings of length 4, 0.25 = p(E3F) = (0.5)$(0.5) = p(E)p(F), so the
events are independent. We can speculate on whether or not the even/odd length
of the bit strings plays a part in the independence characteristic.
Definition: Each performance of an experiment with exactly two outcomes,
denoted success (S) and failure (F), is a Bernoulli trial.
Definition: The Bernoulli distribution is denoted b(k; n,p) = C(n,k)p k q n-k .
Theorem: The probability of exactly k successes in n independent Bernoulli
trials, with probability of success p and failure q = 1 – p is b(k; n,p).
Proof: When n Bernoulli trials are carried out, the outcome is an n-tuple
(t 1 , t 2 , …, t n ), all n t i ,{S, F}. Due to the trials independence, the probability of
each outcome having k successes and n-k failures is p k q n-k . There are C(n,k)
possible tuples that contain exactly k successes and n-k failures.
105
Example: Suppose we generate bit strings of length 10 such that p(0) = 0.7 and
p(1) = 0.3 and the bits are generated independently. Then
• b(8; 10,0.7) = C(10,8)(0.7) 8 (0.3) 2 = 45$0 .0823543$0.09 = 0.3335
• b(7; 10,0.7) = C(10,7)(0.7) 7 (0.3) 3 = 120$0 .05764801$0.027 = 0.1868
n
k=0
Theorem: ! b(k;n,p) = 1.
n
k=0
n
k=0
Proof: ! b(k;n,p) = ! C(k; n,p)p k q n-k = (p+q) n = 1.
Definition: A random variable is a function from the sample space of an
experiment to the set of reals.
Notes:
• A random variable assigns a real number to each possible outcome.
• A random function is not a function nor random.
106

Example: Flip a fair coin twice. Let X(t) be the random variable that equals the
number of tails that appear when t is the outcome. Then
X(HH) = 0, X(HT) = X(TH) = 1, and X(TT) = 2.
Definition: The distribution of a random variable X on a sample space is the set
of pairs (r, p(X=r)) (r,X(S), where p(X=r) is the probability that X takes the
value r.
Note: A distribution is usually described by specifying p(X=r) (r,X(S).
Example: For our coin flip example above, each outcome has probability 0.25.
Hence,
p(X=0) = 0.25, p(X=1) = 0.5, and p(X=2) = 0.25.
107
Definition: The expected value (or expectation) of the random variable X(s) in
the sample space S is E(X)= " p(s)X(s) .
s!S
n
i=1
Note: If S = {x i
} n i=1
, then E(X) = ! p(x i
)X(x i
).
Example: Roll a die. Let the random variable X take the valuess 1, 2, …, 6 with
n
!
$
probability 1/6 each. Then E = 1
' = 3.5. This is not really what you would
i=1"
# 6 %
&
like to see since the die does not a 3.5 face.
Theorem: If X is a random variable and p(X=r) is the probability that X=r so
that p(X=r) = " , then E(X) = " p(X=r)r .
p(s)
r!S,X(s)=r
r!X(S)
Proof: Suppose X is a random variable with range X(S). Let p(X=r) be the
probability that X takes the value r. Hence, p(X=r) is the sum of probabilities of
outcomes s such that X(s)=r Finally, E(X) = " p(X=r)r .
r!X(S)
108

Theorem: If X i , 1;i;n, are random variables on S and if a,b,R, then
1. E(X 1 +X 2 +…+X n ) = E(X 1 )+E(X 2 )+…+E(X n )
2. E(aX i +b) = aE(X i ) + b
Proof: Use mathematical induction (base case is n=2) for 1 and using the
definitions for 2.
Note: The linearity of E is extremely convenient and useful.
Theorem: The expected number of successes when n Bournoulli trials is
performed when p is the probability of success on each trial is np.
Proof: Apply 1 from the previous theorem.
109
Notes:
• The average case complexity of an algorithm can be interpreted as the
expected value of a random variable. Let S={a i }, where each possible input
is an a i . Let X be the random variable such that X(a i ) = b i , the number of
operations for the algorithm with input a i . We assign a probability p(a i )
based on b i . Then the average case complexity is E(X) = " p(a i
)X(a i
).
a i
!S
• Estimating the average complexity of an algorithm tends to be quite
difficult to do directly. Even if the best and worst cases can be estimated
easily, there is no guarantee that the average case can be estimated without a
great deal of work. Frankly, the average case is sometimes too difficult to
estimate. Using the expected value of a random variable sometimes
simplifies the process enough to make it doable.
110

Example of linear search average complexity: See page 44 in the class notes for
the algorithm and worst case complexity bound. We want to find x in a distinct
!
set " a
# i
n
$
%
&i=1
. If x =
!
ai , then there are 2i+1 comparisons. If x6 " a i
!
2n+2 comparisons. There are n+1 input types: " a i
!
where p is the probability that x, " a
# i
n
$
%
&i=1
n
i=1
#
n
$
%
&i=1
. Let q = 14p. So,
E = (p/n)! (2i-1) + (2n+2)q
= (p/n)((n+1) 2 + (2n+2)q
= p(n+2) + (2n+2)q.
There are three cases of interest, namely,
• p = 1, q = 0: E = n + 1
• p = q = 0.5: E = (3n + 4) / 2
• p = 0, q = 1: E = 2n + 2
#
n
$
%
&i=1
, then there are
2x. Clearly, p(ai ) = p/n,
111
Definition: A random variable X has a geometric distribution with parameter p if
p(X=k) = (14p) k-1 p for k = 1, 2, …
Note: Geometric distributions occur in studies about the time required before an
event happens (e.g., time to finding a particular item or a defective item, etc.).
Theorem: If the random variable X has a geometrix distribution with parameter
p, then E(X) = 1/p.
Proof:
E(X) =
!
!
i=1
!
i=1
!
i=1
ip(X=i)
= i(1-p) i-1 p
!
= p i(1-p) i-1
!
= pp -2
= 1/p
112

Definition: The random variables X and Y on a sample space are independent if
p(X(s)=r 1 and Y(S)=r 2 ) = p(X(S)=r 1 )p(Y(S)=r 2 ).
Theorem: If X and Y are independent random variables on a space S, then
E(XY) = E(X)E(Y).
Proof: From the definition of expected value and since X and Y are independent
random variables,
"
E(XY) = X(s)Y(s)p(s)
s!S
= " rtp(X(s)=r and Y(s)=t)
r!X(S),t!Y(S)
"
= rtp(X(s)=r)p(Y(s)=t)
r!X(S),t!Y(S)
= #
& #
% rp(X(s)=r) ( % tp(Y(s)=t)
$ " r!X(S)
= E(X)E(Y).
' $ " t!Y(S)
&
'
(
113
Third Assumption: Not all problems can be solved using deterministic
algorithms. We want to assess the probability of an event based on partial
evidence.
Note: Some algorithms need to make random choices and produce an answer
that might be wrong with a probability associated with its likelihood of
correctness or an error estimate. Monte Carlo algorithms are examples of
probabilistic algorithms.
Example: Consider a city with a lattice of streets. A drunk walks home from a
bar. At each intersection, the drunk must choose between continuing or turning
left or right. Hopefully, the drunk gets home eventually. However, there is no
absolute guarantee.
114

Example: You receive n items. Sometimes all n items are guaranteed to be good.
However, not all shipments have been checked. The probability that an item is
bad in an unchecked batch is 0.1. We want to determine whether or not a
shipment has been checked, but are not willing to check all items. So we test
items at random until we find a bad item or the probability that a shipment
seems to have been checked is 0.001. How items do we need to check? The
probability that an item is good, but comes from an unchecked batch is 140.1 =
0.9. Hence, the k th check without finding a bad item, the probability that the
items comes from an unchecked shipment is (0.9) k . Since (0.9) 66 ~0.001, we must
check only 66 items per shipment.
Theorem: If the probability that an element of a set S does have a particular
property is in (0,1), then there exists an element in S with this property.
115
Bayes Theorem: Suppose that E and F are events from a sample space S such
that p(E) - 0 and p(F) - 0. Then
p(F|E) = p(E|F)p(F) / (p(E|F)p(F) + p(E|F)p(F)).
Generalized Bayes Theorem: Suppose that E is an event from a sample space
n
and that F 1 , F 2 , …, F n are mutually exclusive events such that ! F i
= S.
i=1
Assume that p(E) - 0 and p(F i ) - 0, 1;i;n. Then
n
i=1
p(F j |E) = p(E| F j )p(F j ) / ! p(E|F i
)p(F i
).
116

Example: We have 2 boxes. The first box contains 2 green and 7 red balls. The
second box contains 4 green and 3 red balls. We select a box at random, then a
ball at random. If we picked a red ball, what is the probability that it came from
the first box?
• Let E be the event that we chose a red ball. Thus, E is the event that we
chose a green ball. Let F be the event that we chose a ball from the first box.
Thus, F is the event that we chose a ball from the second box. p(F) = p(F) =
0.5 since we pick a box at random.
• We want to calculate p(F|E) = p(E3F) / p(E), which we will do in stages.
• p(E|F) = 7/9 since there are 7 red balls out of 9 total in box 1. p(E|F) = 3/7
since there are 3 red balls out of a total of 7 in box 2.
• p(E3F) = p(E|F)p(F) = 7/18 = 0.389 and p(E3F) = p(E|F)p(F) = 3/14.
• We need to find p(E). We do this by observing that E = (E3F)2(E3F),
where E3F and E3F are disjoint sets. So, p(E) = p(E3F)+p(E3F) = 0.603.
• p(F|E) = p(E3F) / p(E) = 0.389 / 0.603 = 0.645, which is greater than the 0.5
from the second bullet above. We have improved our estimate!
117
Example: Suppose one person in 100,000 has a particular rare disease and that
there is an accurate diagnostic test for this disease. The test is 99% accurate when
given to someone with the disease and is 99.5% accurate when given to someone
who does not have the disease. We can calculate
(a) the probability that someone who tests positive has the disease, and
(b) the probability that someone who tests negative does not have the disease.
Let F be the event that a person has the disease and let F be the event that this
person tests positive. We will use Bayes theorem to calculate (a) and (b), so have
to calculate p(F), p(F), p(E|F), and p(E|F).
• p(F) = 1 / 100000 = 10 45 and p(F) = 1 4 p(F) = 0.99999.
• p(E|F) = 0.99 since someone who has the disease tests positive 99% of the
time. Similarly, we know that a false negative is p(E|F) = 0.01. Further,
p(E|F) = 0.995 since the test is 99.5% accurate for someone who does not
have the disease.
• p(E|F) = 0.005, which is the probability of a false negative (100 4 99.5%).
118

Now we calculate (a):
p(F|E) = p(E|F)p(F) / (p(E|F)p(F) + p(E|F)p(F)) =
(0.99$10 45 ) / (0.99$10 45 + 0.005$0.99999) = 0.002.
Roughly 0.2% of people who test positive actually have the disease. Getting a
positive should not be an immediate cause for alarm (famous last words).
Now we calculate (b):
p(F|E) = p(E|F)p(F) / (p(E|F)p(F) + p(E|F)p(F))
(0.995$0.99999) / (0.995$0.99999 + 0.01$10 45 ) = 0.9999999.
Thus, 99.99999% of people who test negative really do not have the disease.
119
Bayesian Spam Filters used to be the first line of defense for email programs.
Like many good things, the spammers ran right over the process in about two
years. However, it is an interesting example of useful discrete mathematics.
The filtering involves a training period. Email messages need to be marked as
Good or Bad messages, which we will denote as being the G or B sets.
Eventually the filter will mark messages for you, hopefully accurately.
The filter finds all of the words in both sets and keeps a running total of each
word per set. We construct two functions n G (w) and n B (w) that return the
number of messages containing the word w in the G and B sets, respectively.
We use a uniform distribution. The empirical probability that a spam message
contains the word w is p(w) = n B (w) / |B|. The empirical probability that a nonspam
message contains the word w is q(w) = n G (w) / |G|.
We can use p and q to estimate if an incoming message is or is not spam based
on a set of words that we build dynamically over time.
120

Let E be the event that an incoming message contains the word w. Let S be the
event that an incoming message is spam and contains the word w. Bayes
theorem tells us that the probability that an incoming message containing the
word w is spam is
p(S|E) = p(E|S)p(S) / (p(E|S)p(S) + p(E|S)p(S)).
If we assume that p(S) = p(S) = 0.5, i.e., that any incoming message is equally
likely to be spam or not, then we get the simplified formula
p(S|E) = p(E|S) / (p(E|S) + p(E|S)).
We estimate p(E|S) = p(w) and p(E|S) = q(w). So, we estimate p(S|E) by
r(w) = p(w) / (p(w) + q(w)).
If r(w) is greater than some preset threshold, then we classify the incoming
message as spam. We can consider a threshold of 0.9 to begin with.
121
Example: Let w = Rolex. Suppose it occurs in 250 / 2000 spam messages and in
5 / 1000 good messages. We will estimate the probability that an incoming
message with Rolex in it is spam assuming that it is equally likely that the
incoming message is spam or not. We know that p(Rolex) = 250 / 2000 = 0.125
and q(Rolex) = 5 / 1000 = 0.005. So,
r(Rolex) = 0.125 / (0.125 + 0.005) = 0.962 > 0.9.
Hence, we would reject the message as spam. (Note that some of us would reject
all messages with the word Rolex in it as spam, but that is another case entirely.)
122

Using just one word to determine if a message is spam or not leads to excessive
numbers of false positives and negatives. We actually have to use the
generalized Bayes theorem with a large set of words.
k
i=1
E i
p(S | ! ) =
k
i=1
!
k
i=1
p(E i
|S)
k
i=1
! p(E i
|S) + ! p(E i
|S)
,
which we estimate assuming equal probability that an incoming message is
spam or not by
r(w 1
,w 1
,...,w 1
) =
!
k
i=1
p(w i
)
.
k
k
! p(w i
) + ! q(w i
)
i=1
i=1
123
Example: The word w 1 = stock appears in 400 / 2000 spam messages and in just
60 / 1000 good messages. The word w 2 = undervalued appears in 200 / 2000
spam messages and in just 25 / 1000 good messages. Estimate the likelihood that
an incoming message with both words in it is spam. We know p(stock) = 0.2 and
q(stock) = 0.06. Similarly, p(undervalued) = 0.1 and q(undervalued) = .025. So,
r(stock,undervalued) =
p(stock)p(undervalued)
p(stock)p(undervalued)+q(stock)q(undervalued)
=
0.2!0.1
0.2!0.1+0.06!0.025
= 0.930 > 0.9
Note: Looking for particular pairs or triplets of words and treating each as a
single entity is another method for filtering. For example, enhance performance
probably indicates spam to almost anyone, but high performance computing
probably does not indicate spam to someone in computational sciences (but
probably will for someone working in, say, Maytag repair).
124

Advanced Counting Principles
Definition: A recurrence relation for the sequence {a n } is the equation that
expresses a n in terms of one or more of the previous terms in the sequence. A
sequence is called a solution to a recurrence relation if its terms satisfy the
recurrence relation. The initial conditions specify the values of the sequence
before the first term where the recurrence relation takes effect.
Note: Recursion and recurrence relations have a connection. A recursive
algorithm provides a solution to a problem of size n in terms of a problem size n
in terms of one more instances of the same problem, but of smaller size.
Complexity analysis of the recursive algorithm is a recurrence relation on the
number of operations.
Example: Suppose we have {a n } with a n = 3n, n,N. Is this a solution for
a n = 2a n-1 4 a n-2 for n

Fibonacci Example: A young pair of rabbits (1 male, 1 female) arrive on a
deserted island. They can breed after they are two months old and produce
another pair. Thereafter each pair at least two months old can breed once a
month. How many pairs f n of rabbits are there after n months.
• n = 1: f 1 = 1 Initial
• n = 2: f 2 = 1
conditions
• n > 2: f n = f n-1 + f n-2 Recurrence relation
The n > 2 formula is true since each new pair comes from a pair at least 2
months old.
Example: For bit strings of length n < 3, find the recurrence relation and initial
conditions for the number of bit strings that do not have two consecutive 0’s.
• n = 1: a 1 = 2 Initial {0,1}
• n = 2: a 2 = 3 conditions {01,10,11}
• n > 2: a n = a n-1 + a n-2 Recurrence relation
For n > 2, there are two cases: strings ending in 1 (thus, examine the n41 case)
and strings ending in 10 (thus, examine the n42 case).
127
Definition: A linear homogeneous recurrence relation of degree k with constant
coefficients is a recurrence relation of the form
where {c i },R.
a n = c 1 a n41 + c 2 a n42 + … + c k a n4k ,
Motivation for study: This type of recurrence relation occurs often and can be
systematically solved. Slightly more general ones can be, too. The solution
methods are related to solving certain classes of ordinary differential equations.
Notes:
• Linear because the right hand side is a sum of previous terms.
• Homogeneous because no terms occur that are not multiples of a j ’s.
• Constant because no coefficient is a function.
• Degree k because a n is defined in terms of the previous k sequential terms.
128

Examples: Typical ones include
• P n = 1.15$P n-1 is degree 1.
• f n = f n-1 + f n-2 is degree 2.
• a n = a n-5 is degree 5.
Examples: Ones that fail the definition include
• a n = a n-1 + a2 n-2
is nonlinear.
• H n = 2H n-1 + 1 is nonhomogeneous.
• B n = nB n-1 is variable coefficient.
We will get to nonhomogeneous recurrence relations shortly.
129
Solving a recurrence relation usually assumes that the solution has the form
a n = r n ,
where r,C, if and only if
r n = c 1 r n-1 + c 2 r n-2 + … + c n-k r n-k .
Dividing both sides by r n-k to simplify things, we get
Definition: The characteristic equation is
r k 4 c 1 r k-1 4 c 2 r k-2 4 … 4 c n-k = 0.
Then {a n } with a n = r n is a solution if and only if r is a solution to the
characteristic equation. The proof is quite involved.
The n = 2 case is much easier to understand, yet still multiple cases.
130

Theorem: Assume c 1 ,c 2 ,? 1 ,? 2 ,R and r 1 ,r 2 ,C. Suppose that r 2 4c 1 r4c 2 = 0 has
two distinct roots r 1 and r 2 . Then the sequence {a n } is a solution to the
recurrence relation a n = c 1 a n-1 + c 2 a n-2 if and only if a n = ! 1
r 1
n + ! 2
r 2
n for n,N 0 .
Example: a 0 = 2, a 1 = 7, and a n = a n-1 + 2a n-2 for n

Now comes the second case for n = 2.
Theorem: Assume c 1 ,c 2 ,? 1 ,? 2 ,R and r 0 ,C. Suppose that r 2 4c 1 r4c 2 = 0 has one
root r 0 with multiplicity 2. Then the sequence {a n } is a solution to the recurrence
relation a n = c 1 a n-1 + c 2 a n-2 if and only if a n = ! 1
r 0
n + ! 2
nr 0
n for n,N 0 .
Example: a 0 = 1, a 1 = 6, and a n = 6a n-1 4 9a n-2 for n

Theorem: Let {c i
} k
i=i
, {! i
} k i=i
,R and {r i
} k i=i
,C. Suppose the characteristic
equation r k – c 1 r k41 4… 4 c k = 0 has t distinct roots r i , 1;i;t, with multiplicities
t
m i ,N such that ! m i
= k . Then the sequence {a
i=1
n } is a solution of the
recurrence relation a n = c 1 a n41 + c 2 a n42 + … + c k a n4k if and only if
a n = (! 1,0
+! 1,1
n+...+! 1,m1 "1 nm 1 "1 )r 1
n + ... + (! t,0
+! t,1
n+...+! t,mt "1 nm t "1 )r t
n
for n,N 0 and all ? i,j , 1;i;t and 0;j;m i 41.
Example: Suppose the roots of the characteristic equation are 2, 2, 3, 3, 3, 5.
Then the general solution form is
(? 1,0 +? 1,1 n)2 n + (? 2,0 +? 2,1 n+? 2,2 n 2 )3 n + ? 3,0 5 n .
With given initial conditions, we can even compute the ?’s.
135
Definition: A linear nonhomogeneous recurrence relation of degree k with
constant coefficients is a recurrence relation of the form
where {c i },R.
a n = c 1 a n41 + c 2 a n42 + … + c k a n4k + F(n),
Theorem: If {a n (p) } is a particular solution of the recurrence relation with
constant coefficients a n = c 1 a n41 + c 2 a n42 + … + c k a n4k + F(n), then every solution
is of the form {a n (p) +a n (h) }, where {a n (h) } is a solution of the associated
homogeneous recurrence relation (i.e., F(n) = 0).
Note: Finding particular solutions for given F(n)’s is loads of fun unless F(n) is
rather simple. Usually you solve the homogeneous form first, then try to find a
particular solution from that.
136

Theorem: Assume {b i },{c i },R. Suppose that {a n } satisfies the nonhomogeneous
recurrence relation
and
a n = c 1 a n41 + c 2 a n42 + … + c k a n4k + F(n)
f(n) = (b t n t + b t-1 n t-1 + … + b 1 n + b 0 )s n .
When s is not a root of the characteristic equation of the associated
homogeneous recurrence relation, there is a particular solution of the form
(p t n t + p t-1 n t-1 + … + p 1 n + p 0 )s n .
When s is a root of multiplicity m of the characteristic equation, there is a
particular solution of the form
n m (p t n t + p t-1 n t-1 + … + p 1 n + p 0 )s n .
Note: If s = 1, then things get even more complicated.
137
Example: Let a n = 6a n-1 – 9a n-2 + F(n). When F(n) = 0, the characteristic equation
is (r43) 2 . Thus, r 0 = 3 with multiplicity 2.
• F(n) = 3 n : particular solution is n 2 p 0 3 n .
• F(n) = n3 n : particular solution is n 2 (p 1 n + p 0 )3 n .
• F(n) = n 2 2 n : particular solution is (p 2 n 2 + p 1 n + p 0 )2 n .
• F(n) = (n+1)3 n : particular solution is n 2 (p 2 n 2 + p 1 n + p 0 )3 n .
Definition: Suppose a recursive algorithm divides a problem of size n into m
subproblems of size n/m each. Also suppose that g(n) extra operations are
required to combine the m subproblems into a solution of the problem of size n.
If f(n) is the cost of solving a problem of size n, then the divide and conquer
recurrence relation is f(n) = af(n/b) + g(n).
We can easily work out a general cost for the divide and conquer recurrence
relation using Big-Oh notation.
138

Divide and Conquer Theorem: Let a,b,c,R and be nonnegative. The solution to
the recurrence relation
!
# c, for n = 1,
f(n) = "
# af(n/b)+cn d , for n > 1,
for n a power of b is
$
!
# O(n d ),
#
f(n)= O(n d logn),
"
#
#
$ #
O(n log b a ),
for a < b d ,
for a = b d ,
for a > b d .
log b
n
i=1
Proof: If n is a power of b, then for r = a/b, f(n) = cn! r i . There are 3 cases:
!
i=0
• a < b d : Then ! r i converges, so f(n) = O(n d ).
• a = b d : Then each term in the sum is 1, so f(n) = O(n d logn).
• a > b d : Then cn d log b
n
! r
i=1
i = cn d " r1+log b n -1
which is O(a log b n ) or O(n log b a ).
r-1
139
Example: Recall binary search (see page 45 in the class notes). Searching for an
element in a set requires 2 comparisons to determine which half of the set to
search further. The search keeps halving the size of the set until at most 1
element is left. Hence, f(n) = f(n/2) + 2. Using the Divide and Conquer theorem,
we see that the cost is O(logn) comparisons.
Example: Recall merge sort (see pages 81-83 in the class notes). This sorts
halves of sets of elements and requires less than n comparisons to put the two
sorted sublists into a sorted list of size n. Hence, f(n) = 2f(n/2) + n. Using the
Divide and Conquer theorem, we see that the cost is O(nlogn) comparisons.
Multiplying integers can be done recursively based on a binary decomposition
of the two numbers to get a fast algorithm. The patent on this technique,
implemented in hardware, made a computer company several billion dollars
back when a billion dollars was real money (cf. a trillion dollars today).
Why stop with integers? The technique extends to multiplying matrices, too,
with real, complex, or integer entries.
140

Example (funny integer multiplication): Suppose a and b have 2n length binary
representations a = (a 2n41 a 2n42 … a 1 a 0 ) 2 and a = (b 2n41 b 2n42 … b 1 b 0 ) 2 . We will
divide a and b into left and right halves:
The trick is to notice that
a = 2 n A 1 + A 0 and , where b = 2 n B 1 + B 0 and
A 1 = (a 2n41 a 2n42 …a n+1 a n ) 2 and A 0 = (a n-1 a n42 …a 1 a 0 ) 2 ,
B 1 = (b 2n41 b 2n42 …b n+1 b n ) 2 and B 0 = (b n-1 b n42 …b 1 b 0 ) 2 .
ab = (2 2n +2 n )A 1 B 1 + 2 n (A 1 4A 0 )(B 0 4B 1 ) + (2 n +1)A 0 B 0 .
Only 3 multiplies plus adds, subtracts, and shifts are required. So, f(2n) = 3f(n)
+ Cn, where C is the cost of the adds, subtracts, and shifts. The Divide and
Conquer theorem tells us this O(n log3 ), which is about O(n 1.6 ). The standard
algorithm is O(n 2 ). It might not seem like much of an improvement, but it
actually is when lots of integers are multiplied together. The trick can be applied
recursively on the three multiplies in the ab line (halving 2n in the recursion).
141
Example (Strassen-Winograd Matrix-Matrix multiplication): We want to
multiply A: m$k by B: k$n to get C: m$n. The matrix elements can be reals,
complex numbers, or integers. When m = k = n, this takes O(n 3 ) operations
using the standard matrix-matrix multiplication algorithm. However, Strassen
first proposed a divide and conquer algorithm that reduced the exponent. The
belief is that someday, someone will devise an O(n 2 ) algorithm. Some hope it
will even be plausible to use such an algorithm. The variation of Strassen’s
algorithm that is most commonly implemented by computer vendors in high
performance math libraries is the Winograd variant. It computes the product as
A 11
A 12
A 21
A 22
!
#
#
#
"
$ !
& #
& #
& #
% "
B 11
B 12
B 21
B 22
$
&
&
&
%
!
"
$
&
&
&
%
= C 11 C # 12
# .
# C 21
C 22
C is computed in 22 steps involving the submatrices of A, B, and intermediate
temporary submatrices. An interesting question for many years was how little
extra memory was needed to implement the Strassen-Winograd algorithm (see
C. C. Douglas, M. Heroux, G. Slishman, and R. M. Smith, GEMMW: A
142

portable Level 3 BLAS Winograd variant of Strassen's matrix-matrix multiply
algorithm, Journal of Computational Physics, 110 (1994), pp. 1-10 for an
answer).
The 22 steps are the following:
Step W mk C 11 C 12 C 21 C 22 W kn Operation
1 S 7 B 22 4B 12
2 S 3 A 11 4A 21
3 M 4 S 3 S 7
4 S 1 A 21 +A 22
5 S 5 B 12 4B 11
6 M 5 S 1 S 5
7 S 6 B 22 4S 5
8 S 2 S 1 4A 11
9 M 1 S 2 S 6
10 S 4 A 12 4S 2
143
Step W mk C 11 C 12 C 21 C 22 W kn Operation
11 M 6 S 4 B 22
12 T 3 M 5 +M 6
13 M 2 A 11 B 11
14 T 1 M 1 +M 2
15 C 12 T 1 +T 3
16 T 2 T 1 +M 4
17 S 8 S 6 4B 21
18 M 7 A 22 S 8
19 C 21 T 2 4M 7
20 C 22 T 2 +M 5
21 M 3 A 12 B 21
22 C 11 M 2 +M 3
There are four tricky steps in the table above, depending on whether or not k is
even or odd. Each step makes certain that we do not use more memory than is
allocated for a submatrix or temporary. For example,
144

• In step 4, we have to take care that with S 1 . (a) If k is odd, then copy the
first column of A 21 into W mk . (b) Complete S 1 .
• In step 10, we have to take care that with S 4 . (a) If k is odd, then pretend the
first column of A 21 = 0 in W mk . (b) Complete S 4 .
• In step 11, we have to take care that with M 6 . (a) If m is odd, then save the
first row of M 5 . (b) Calculate most of M 6 . (c) Complete M 6 using (a) based
on whether or not m is odd.
• In step 21, we have to take care that with M 3 . (a) Caluclate M 3 using an
index shift.
This all sounds very complicated. However, the code GEMMW that is readily
available on the Web effectively is implemented in 27 calls to subroutines that
do the matrix operations and actually implements
C = ?Cop(A)op(B) + DCC,
where op(X) is either X, X transpose, X conjugate, or X conjugate transpose.
145
What is the total cost?
• There are 7 submatrix-submatrix multiplies and 15 submatrix-submatrix
adds or subtracts. So the cost is f(n) = 7f(n/2) + 15n 2 /4 when m=k=n. This is
actually an O(n 2.807 logn) algorithm, where log 2 7 = 2.807.
• The work area W mk needs 7((m+1)max(k,n)+m+4)/48 space.
• The work area W kn needs 7((k+1)n+n+4)/48 space.
• If C overlaps A or B in memory, an additional mn space is needed to save C
before calculating DCC when D-0.
• The maximum amount of extra memory is bounded by
(mCmax(k,n)+kn)/3+(m+max(k,n)+k+3n)/2+32+mn. Hence, the overall
extra storage is cN 2 /3, where c,{2,5}.
• Typical memory usage when m=k=n is
o D-0 or A or B overlap with C: 1.67N 2 .
o D=0 and A and B do not overlap with C: 0.67N 2 .
146

Definition: The (ordinary) generating function for a sequence a 1 , a 2 , …, a k , … of
!
real numbers is the infinite series G(x) = " a k
x
k=0
k . For a finite sequence
{a k
} n
n
k=0
, the generating function is G(x) = ! a k
x k .
Examples:
!
1. a k = 3, G(x) = 3" x
k=0
k .
!
2. a k = k+1, G(x) = " (k+1)x
k=0
k .
3. a k = 2 k !
, G(x) = " (2x)
k=0
k .
2
4. a k = 1, 0;k;2, G(x) = ! x
k=0
k = x3 "1
x"1 .
Notes:
• x is a placeholder, so that G(1) in example 4 above is undefined does not
matter.
• We do not have to worry about convergence of the series, either.
k=0
147
• When solving a series using calculus, knowing the ball of convergence for
the x’s is required.
Lemma: f(x) = (14ax) 41 is the generating function for the sequence 1, (ax), (ax) 2 ,
…, (ax) k , … since for a-0 and |ax|

Definition: The extended binomial coefficient u # &
# k
for u,R and k,N 0 is defined
&
by
!
#
"
#
u
k
$
&
%
&
'
)
=
u(u-1)!(u-k+1)/k! if k > 0,
(
) 1 if k = 0.
*
Extended Binomial Theorem: If u,x,R such that |x|

Note: Generating functions can be used to solve many counting problems.
Examples:
• How many solutions are there to the constrained problem a+b = 9 for 3;a;5
and 4;b;6? There are 3 total. The number of solutions with the constraints
is the coefficient of x 9 in (x 3 +x 4 +x 5 )(x 4 +x 5 +x 6 ). We choose x a and x b from
the two factors, respectively, so that a+b = 9. By inspection, there are only 3
choices for a and b.
• How many ways can 8 CPUs be distributed in 3 servers if each server gets
2-4 CPUs each? The generating function is f(x) = (x 2 +x 3 +x 4 ) 3 . We need the
coefficient of x 8 in f(x). Expansion of f(x) gives us 6 ways.
Note: Maple or Mathematica is really useful in the examples above.
151
Note: Generating functions are useful in solving recurrence relations, too.
Example: a k = 3a k41 , k > 0 with a 0 = 2. Let f(x) = " a k
x k be the generating
"
function for {a k }. Then xf(x) = # a k!1
x
k=1
k . Using the recurrence relation
directly, we have
!
k=0
!
k=0
f(x) – 3xf(x) = ! a k
x k " 3!
a k"1
x
k=1
k
!
= a 0
+ (a k
! 3a k!1
)x k
= a 0
= 2
"
Hence, f(x) 4 3xf(x) = (143x)f(x) = 2 or f(x) = 2 / (143x). Using the identity for
(14ax) 41 , we see that
!
k=0
k=1
f(x) = " 2!3 k x k or a k
= 2!3 k .
!
152

Example: a n = 8a n41 + 10 n41 with a 0 = 1, which gives us a 1 = 9. Find a n in closed
form. First multiply the recurrence relation by x n to give us
a n x n + 8a n!1
x n + 10 n-1 x n !
. If f(x) = " a k
x k , then
f(x) 4 1 =
!
!
!
k=1
!
k=1
k=0
a k
x k
= (8a k-1
x k +10 k-1 x k )
= 8xf(x) + x/(1410x)
Hence,
f(x) = 1!9x
(1!8x)(1!10x)
= 1 "
1
2 1!8x + 1!10x
1
$
$
'
#
!
k=0
!
%
'
'
&
= 1 8 k +10 k
2
#
&x k
or a n = .5(8 k +10 k ).
"
$
%
153
Note: It is possible to prove many identities using generating functions.
Exclusion-Inclusion Theorem: Given sets A i , 1;i;n, the number of elements in
the union is
n
i=1
A i
n
i=1
"
! = ! A i
! 1!i

Example: A factory produces vehicles that are car or truck based: 2000 could be
cars, 4000 could be trucks, and 3200 are SUV’s, which can be car or truck based
(depending on the frames). How many vehicles were produced? Let A 1 be the
number of cars and A 2 be the number of trucks. There are
A 1
!A 2
= A 1
+ A 2
! A 1
"A 2
= 2000 + 4000 ! 3200 = 2800.
Theorem: The number of onto functions from a set of m elements to a set of n
elements with m,n,N is
n m 4 C(n,1)(n41) m41 + C(n,2) )(n41) m41 4 … + (41) n41 C(n,n41).
155
Definition: A derangement is a permutation of objects such that no object is in
its original position.
Theorem: The number of derangements of a set of n elements is
#
"
n
D n = 1! (!1) k 1
%
(
% k=1
n! k! (
$
Example: I hand back graded exams randomly. What is the probability that no
student gets his or her own exam? It is P n = D n / n! since there are n! possible
permutations. As n%., P n %e 41 .
&
'
156

Relations
Definition: A relation on a set A is a subset of A$A.
Definition: A binary relation between two sets A and B is a subset of A$B. It is
a set R of ordered pairs, denoted aRb when (a,b),R and aRbwhen (a,b)6R.
Definition: A n-ary relation on n sets A 1 , …, A n is a subset of A 1 $…$A n . Each
A i is a domain of the relation and n is the degree of the relation.
Examples:
• Let f: A%B be a function. Then the ordered pairs (a,f(a)), (a,A, forms a
binary relation.
• Let A = {Springfield} and B = {U.S. state | )Springfield in the state}. Then
(Springfield,U.S. states) is a relation with about 44 elements (the so-called
Simpsons relation).
157
Theorem: Let A be a set with n elements. There are 2 n2 unique relations on A.
Proof: We know there are n 2 elements in A$A and that there are 2 m possible
subsets of a set with m elements. Hence, the result.
Definitions: Consider a relation R on a set A. Then
• R is reflexive if (a,a),R, (a,A.
• R is symmetric if (a,b),R and (b,a),R, (a,b,A.
• R is antisymmetric if (a,b),R and (b,a),R, then a=b, (a,b,A.
• R is transitive if (a,b),R and (b,c),R, then (a,c),R, (a,b,c,A.
Theorem: Let A be a set with n elements. There are 2 n(n41) unique transitive
relations on A.
Proof: Each of the n pairs (a,a),R. The remaining n(n41) pairs may or may not
be in R. The product rule and previous theorem give the result.
158

Examples: Let A = {1, 2, 3, 4}.
• R 1 = {(1,1), (1,2), (2,1), (2,2), (3,4), (4,1), (4,4)} is
o just a relation
• R 2 = {(1,1), (1,2), (2,1)} is
o symmetric
• R 3 = {(1,1), (1,2), (1,4), (2,1), (2,2), (3,3), (4,1), (4,4)} is
o reflexive and symmetric
• R 4 = {(2,1), (3,1), (3,2), (4,1), (4,2), (4,3)} is
o antisymmetric and transitive
• R 5 = {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,3), (3,4), (4,1),
(4,4)} is
o reflexive, antisymmetric, and transitive
• R 6 = {(3,4)} is
o antisymmetric
Note: We will come back to these examples when we get around to
representations of relations that work in a computer.
159
Note: We can combine two or more relations to get another relation. We use
standard set operations (e.g., 3, 2, #, 4, …).
Definition: Let R be a relation on a set A to B and S a relation on B to a set C.
Then the composite of R and S is the relation S!R such that if (a,b),R and
(b,c),S, then (a,c), S!R, where a,A, b,B, and c,C.
Definition: Let R be a relation on a set A. Then R n is defined recursively: R 1 = R
and R n =R n!1 !R , n>1.
Theorem: The relation R is transitive if and only if R0R n , n

Representation: The relation R from a set A to a set B can be represented by a
zero-one matrix M R = [m ij ], where
#
m ij
= 1 if (a i ,b j )!R,
%
$
% 0 if (a i
,b j
)"R.
Notes:
&%
• This is particularly useful on computers, particularly ones with hardware bit
operations for packed words.
• M R contains I for reflexive relations.
• M R
= M R
T for symmetric relations.
• m ij = 0 or m ji = 0 when i-j for antisymmetric relations.
161
Examples:
• M R
=
• M R
=
1 1 0
1 1 1
0 1 1
!
#
#
#
#
"
#
!
#
#
#
#
"
#
$
&
&
&
&
%
&
$
&
&
&
&
%
&
is transitive and symmetric.
0 1 0
0 0 0 is antisymmetric.
0 1 0
162

Representation: A relation can be represented as a directed graph (or digraph).
For (a,b),R, a and b are vertices (or nodes) in the graph and a directional edge
runs from a to b.
Example: The following digraph represents {(a,b), (b,c), (c,a), (c,b)}.
a" " b
" c
What about all of those examples on page 159 of the class notes? We can do all
of them over in either representation.
163
Examples (from page 159):
!
# 1 1 0 0
#
• M R1
= #
1 1 0 0
#
#
0 0 0 1
#
1 0 0 1
"#
!
#
#
#
#
#
#
"#
!
#
#
#
#
#
#
"#
$
&
&
&
&
&
&
%&
$
&
&
&
&
&
&
%&
$
&
&
&
&
&
&
%&
1 1 0 0
• M R2
=
1 0 0 0
0 0 0 0
0 0 0 0
1 1 0 1
• M R3
=
1 1 0 0
0 0 1 0
1 0 0 1
or a digraph a 1 " " a 2
164

!
# 0 0 0 0
#
• M R4
= #
1 0 0 0
#
#
1 1 0 0
#
1 1 1 0
"#
!
#
#
#
#
#
#
"#
!
#
#
#
#
#
#
"#
1 1 1 1
• M R5
=
1 1 1 1
0 0 1 0
1 0 0 1
0 0 0 0
• M R6
=
0 0 0 0
0 0 0 1
0 0 0 0
$
&
&
&
&
&
&
%&
$
&
&
&
&
&
&
%&
$
&
&
&
&
&
&
%&
or the digraph a 3 " " a 4
165
Definition: A relation on a set A is an equivalence relation if it is reflexive,
symmetric, and transitive. Two elements a and b that are related by an
equivalence relation are called equivalent and denoted a~b.
Examples:
• Let A = Z. Define aRb if and only if either a = b or a = 4b.
o symmetric: aRa since a = a.
o reflexive: aRb E bRa since a = ±b.
o transitive: aRb and bRc E aRc since a = ±b = ±c.
• Let A = R. Define aRb if and only if a4b,Z.
o symmetric: aRa since a4a = 0,Z.
o reflexive: aRb E bRa since a4b,Z E 4(a4b) = b4a,Z.
o transitive: aRb and bRc E aRc since (a4b)+(b4c) ,Z E a4c,Z.
166

Definition: Let R be an equivalence relation on a set A. The set of all elements
that are related to an element a,A is called the equivalence class of a and is
denoted by [a] R . When R is obvious, it is just [a]. If b,[a] R , b is called a
representative of this equivalence class.
Example: Let A = Z. Define aRb if and only if either a = b or a = 4b. There are
two cases for the equivalence class:
• [0] = {0}
• [a] = {a, 4a} if a-0.
167
Theorem: Let R be an equivalence relation on a set A. For a,b,A, the following
are equivalent:
1. aRb
2. [a] = [b]
3. [a] 3 [b] - /.
Proof: 1 E 2 E 3 E 1.
• 1 E 2: Assume aRb. Suppose c,[a]. Then aRc. Due to symmetry,
we know that bRa. Knowing that bRa and aRc, by transitivity,
bRc. Hence, c,[b]. A similar argument shows that if c,[b], then
c,[a]. Hence, [a] = [b].
• Assume that [a] = [b]. Since a,A and R is reflexive, [a] 3 [b] - /.
• Assume [a] 3 [b] - /. So there is a c,[a] and c,[b], too. So, aRc
and bRc. By symmetry, cRb. By transitivity, aRc and cRb, so aRb.
Lemma: For any equivalence relation R on a set A, [a] R
=A
a!A ! .
Proof: For all a,A, a,[a] R .
168

Definition: A partition of a set S is a collection of disjoint sets whose union is A.
Theorem: Let R be an equivalence relation on a set S. Then the equivalence
classes of R form a partition of S. Conversely, given a partition {A i | i,I} of the
set S, there is an equivalence relation R that has the sets A i , i,I, as its
equivalence classes.
169
Graphs
Definition: A graph G = (V,E) consists of a nonempty set of vertices V and a set
of edges E. Each edge has either one or two vertices as endpoints. An edge
connects its endpoints.
Note: We will only study finite graphs (|V| < .).
Categorizations:
• A simple graph has edges that connects two different vertices and no two
edges connect the same vertex.
• A multigraph has multiple edges connecting the same vertices.
• A loop is a set of edges from a vertex back to itself.
• A pseudograph is a graph in which the edges do not have a direction
associated with them.
• An undirected graph is a graph in which the edges do not have direction.
• A mixed graph has both directed and undirected edges.
170

Definition: Two vertices u and v in an undirected graph G are adjacent (or
neighbors) in G if u and v are endpoints of an edge e in G. Edge e is incident to
{u,v} and e connects u and v.
Definition: The degree of a vertex v, denoted deg(v), in an undirected graph is
the number of edges incident with it except that loops contribute twice to the
degree of that vertex. If deg(v) = 0, then it is isolated. If deg(v) = 1, then it is a
pendant.
Handshaking Theorem: If G = (V,E) is an undirected graph with e edges, then
#
&
e= % deg(v) ( /2.
$
" v!V
'
Proof: Each edge contributes 2 to the sum since it is incident to 2 vertices.
Example: Let G = (V,E). Suppose |V| = 100,000 and deg(v) = 4 for all v,V.
Then there are (4$100,000)/2 = 200,000 edges.
171
Theorem: An undirected graph has an even number of vertices and an odd
degree.
Definition: Let (u,v),E in a directed graph G(V,E). Then u and v are the initial
and terminal vertices of (u,v), respectively. The initial and terminal vertices of a
loop (u,u) are both u.
Definition: The in-degree of a vertex, denoted deg 4 (v), is the number of edges
with v as their terminal vertex. The out-degree of a vertex, denoted deg + (v), is
the number of edges with v as their initial vertex.
Theorem: For a directed graph G(V,E), # deg ! (v) = deg
v"V # + (v) = E .
v"V
172

Examples of Simple Graphs:
• A complete graph has an edge between any vertex.
• A cycle C n is a graph with |V|

Representation: For graphs without multiple edges we can use adjacency lists or
matrices. For general graphs we can use incidence matrices.
Definition: Let G(V,E) have no multiple edges. The adjacency list L G = {a v } v,V ,
where a v = adj(v) = {w,V | w is adjacent to v}.
Definition: Let G(V,E) have no multiple edges. The adjacency matrix A G = [a ij ]
is
!
a ij
= 1 if {v i ,v # } is an edge of G,
j
"
# 0 otherwise.
Example:
$
v 1
v 2
v 4
v 3
results in A G
=
0 1 1 0
1 0 0 1
1 0 0 1
0 1 1 0
!
#
#
#
#
#
#
"#
$
&
&
&
&
&
&
%&
and L G
=
v 1
:
v 2
:
v 3
:
v 4
:
!
#
#
"
#
#
#
$
v 2
,v 3
v 1
,v 4
v 1
,v
.
4
v 2
,v 3
175
Note: For an undirected graph, A G
= A G T . However, this is not necessarily true
for a directed graph.
Definition: The incidence matrix M = [m ij ] for G(V,E) is
!
m ij
= 1 when edge e i is incident with v j ,
#
"
# 0 otherwise.
$
Definition: The simple graphs G(V,E) and H = (W,F) are isomorphic if there is
an isomorphism f: V%W, a one to one, onto function, such that a and b are
adjacent in G if and only if f(a) and f(b) are adjacent in H for all a,b,V.
176

Examples:
v 1
v 2
•
and
v 4
v 3
v 1
v 2
v 3
v 4
are not isomorphic.
v 1
v 2
•
and
v 3
v 4
v 1
v 2
v 4
v 3
are isomorphic.
Note: Isomorphic simple graphs have the same number of vertices and edges.
Definition: A property preserved by graph isomorphism is called a graph
invariant.
Note: Determining whether or not two graphs are isomorphic has exponential
worst case complexity, but linear average case complexity using the bet
algorithms known.
177
Definition: Let G = (V,E) be an undirected graph and n,N. A path of length n
for u,v,V is a sequence of edges e 1 , e 2 , …, e n ,E with associated vertices in V
of u = x 0 , x 1 , …, x n = v. A circuit is a path with u = v. A path or circuit is simple
if all of the edges are distinct.
Notes:
• We already defined these terms for directed graphs.
• The terminal vertex of the first edge in a path is the initial vertex of the
second edge. We can define a path using a recursive definition.
Definition: An undirected graph is connected if there is a path between every
pair of distinct vertices in the graph.
178

Theorem: There is a simple path between every distinct pair of vertices of a
connected undirected graph G = (V,E).
Proof: Let u,v,V such that u - v. Since G is connected, there is a path from u to
v that has minimum length n. Suppose this path is not simple. Then in this
minimum length path, there is some pair of vertices x i =x j ,V for some 0;i

Theorem: Let G = (V,E) be a graph with adjacency matrix A. The number of
different paths of length n from v i to v j , where v i ,v j ,V and n,N, is the (i,j) entry
in A n .
Example:
v 1
v 2
v 4
v 3
A =
0 1 1 0
1 0 0 1
1 0 0 1
0 1 1 0
!
#
#
#
#
#
#
"#
$
&
&
&
&
&
&
%&
and A 4 =
8 0 0 8
0 8 8 0
0 8 8 0
8 0 0 8
!
#
#
#
#
#
#
"#
$
&
&
&
&
&
&
%&
Note: The theorem can be used to find the shortest path between any two
vertices and also to determine if a graph is connected.
181
Definition: Let G = (V,E) have an associated weighting function w(u,v):
V$V%R. G is called a weighted graph. The weighted length of a path in G is
the sum of the weights for the edges in the path.
Example: Let G = (V,E) be a weighted graph where V represents airports. Then
some interesting weighting functions include the following between pairs of
distinct airports:
• Distance
• Flight times
• Airfares
• Frequent flier miles
• Frequent flier qualification miles
Note: Weighted graphs are extremely important in analyzing transportation of
goods and people and trying to minimize time and expenses.
182

Dijkska’s Algorithm (Shortest Path) – [published in 1959]
Procedure Dijkstra( G = (V,E) with w: V$V%R + . G is a weighted connected
simple graph,
a,z,V: initial and terminal vertices )
for i := 1 to n
L(i) := .
L(a) := 0
S := /
while z6S
u := a vertex not in S with L(u) minimal
S := S2{u}
for all v,V such that v6S
if L(u) + w(u,v) < L(v) then L(v) := L(u,v) + w(u,v)
{ L(z) = length of shortest path from a to z. }
183
Theorem: Dijkstra’s algorithm finds the length of the shortest path between two
vertices in a connected simple undirected weighted graph. The algorithm uses
O(n 2 ) comparison and addition operations.
Traveling Salesman Problem: Find the circuit of minimum total weight in a
weighted complete undirected graph that visits every vertex exactly once and
returns to its starting vertex.
Note: There are n! possible circuits to consider, which is intractable when n is
sufficiently large. A tremendous amount of research has been devoted to finding
fast approximate solution algorithms. The best ones can produce a circuit of
length 1,000 in a few seconds and still be within 2% of the optimum circuit.
184

Definition: A coloring of a simple graph is the assignment of a color to each
vertex of the graph so that no adjacent vertices are assigned the same color.
Definition: The chromomatic number F(G) is the least number of colors needed
for a coloring of the graph G = (V,E).
Definition: A planar graph is a graph that can be drawn in a plane with no edges
crossing in the picture.
Four Color Theorem: If G is a planar graph, then F(G) ; 4.
Note: The Four Color Conjecture was made in the 1850’s and not proven until
1976. Like Fermat’s last theorem, this theorem became famous partly for how
many wrong proofs (some quite ingenious) were either published or submitted
for publication.
185
Trees
Definition: A tree is a connected undirected graph with no simple circuits. A
weighted tree is a tree with weights associated with the edges.
Uses:
• An efficient data structure for searching a list.
o Useful in encoding data for transmission.
o Computational complexity easily determined for algorithms using trees.
• Weighted trees have edges with weights.
o Useful in decision making.
o Used by telecoms to dynamically connect calls cheaply.
Historical Note: Trees were first developed in the context of this course to
describe molecules in chemistry, where atoms were the vertices and bonds were
the edges.
186

Theorem: An undirected graph T = (V,E) is a tree if and only if there is a unique
simple path between any two of its distinct vertices.
Proof:
1. Assume T is a tree, so it has no simple circuits. Since T is connected, for all
distinct u,v,V, there is exactly one simple path between u and v.
Otherwise, there is another simple path. Combining the two simple paths is
a circuit, which is a contradiction that T is a tree.
2. Assume that there is a unique simple path between any two distinct vertices
u,v,V. The T is connected. T has no simple circuits since then there would
be two simple paths between u and v (thus forming a crcuit), which is a
contradiction.
Definition: A rooted tree is a tree with one vertex designated as the root and
every edge is directed away from the root.
Note: Any tree can become a rooted tree by picking the right vertex as the root.
187
Terminology/Definitions: Let T = (V,E) be a rooted tree. Then
• If v,V is not a root of, the parent w,V of v is a vertex with an edge
directed at v and v is a child of u.
• If v i ,V are children of the same u,V, they are siblings.
• The ancestors v i ,V of u,V are any vertices in V except the root which are
in the path from the root to u.
• The descendents v i ,V of u,V are all vertices with u as an ancestor.
• A leaf v,V is a vertex with no children.
• An internal vertice v,V has children.
• A subtree is the subgraph formed from a,V and all of its descendents and
the edges incident to these descendents.
• The height of a rooted tree T, denoted h(T), is the maximum number of
levels (or vertices).
• A balanced rooted tree T has all of its leaves at h(T) or h(T)-1.
188

Definition: A m-ary tree is a rooted tree such that every internal vertex has no
more than m children. A full m-ary tree is a rooted tree such that every internal
vertex has exactly m children. If m = 2, it is a (full) binary tree.
Definition: An ordered rooted tree is a rooted tree with an ordering applied to
the children of all of the children of the root and the internal vertices.
Examples:
• Management charts
• Directory based file or memory systems
Theorem: A tree with n vertices has n41 edges.
The proof is by mathematical induction.
Theorem: A full m-ary tree with i internal vertices contains n = mi+1 vertices.
Proof: There are mi children plus the root.
189
Theorem: A full m-ary tree with
• n vertices has i = (n41)/m internal vertices and q = [(m41)n+1]/m leaves.
• i internal vertices has n = m+1 vertices and q = (m41)i + 1 leaves.
• q leaves has n = (mq41) / (m41) vertices and i = (q41) / (m41) internal
vertices.
Theorem: There are at most m h leaves in a m-ary tree of height h.
The proof uses mathematical induction.
Corollary: If an m-ary tree of height h has q leaves, then h < 9log m q:. For a full
m-ary and balnced m-ary tree, h = 9log m q:.
190

Definition: A binary search tree T = (V,E) is a binary tree with a key for each
vertex. The keys are ordered such that a key for a vertex is greater in value than
all keys associated with its left subtree and less in value than all keys associated
with its right subtree. The key for vertex v,V is denoted by label(v).
Note: Recursive algorithms search binary trees for keys in O(log h n) operations
for a binary tree of height h and with n vertices.
Notation: Let T = (V,E) be a binary tree.
• Let root(T) be the root vertex in T.
• Let left_child(v) and right_child(v) refer to the left or right child of a root or
internal vertice v in a binary tree.
• Let add_new_vertex(parent, value) add a new left or right vertex to the
parent vertex with a key of value. The details are left intentionally fuzzy.
Note: One of the most common operation with a binary tree is to search it.
Another is to search a binary tree for a key and add it if it is missing.
191
procedure insertion( T = (V,E): binary tree, x: item )
v := root(T)
while v - / and label(v) - x
if x < label(v) then
if left_child(v) - / then
v := left_child(v)
else
add_new_vertex(left_child(v), x) and v = /
else
if right_child(v) - / then
v := right_child(v)
else
add_new_vertex(right_child(v), x) and v = /
if root(T) = / then
add_new_vertex(T, x)
else if v = / or label(v) = / then
label the new vertex x and set v := the new vertex
{ v = location of x. }
192

Definition: A decision tree is a rooted tree in which the children are the possible
outcomes of their ancestors’ keys.
Note: There is usually a weighting associated with a decision tree. The keys may
not be unique.
Definition: A prefix code is an encoding based on bit strings representing
symbols such that a symbol, as a bit string, never occurs as the first part of
another symbol’s bit string.
Example: We can represent normally a-z in 5 bits and a-zA-Z in 6 bits. Suppose
we only have 3 letters: a = 0, c = 10, and t = 11. Then cat = 10011. Wowee! We
saved one whole bit!!!
Representation: Prefix codes form a binary tree.
193
Example: The prefix code for a = 0, c = 10, and t = 11 is stored as
•
0 1
a • •
0 1
c • t •
Definition: A Huffman coding takes the frequency of symbols and is the prefix
code with the smallest number of bits.
Note: Huffman coding was a course project by a graduate student at MIT in the
1950’s. Needless to say, his professor was stunned.
194

procedure Huffman(a i : symbols, w i : frequencies, 1;i;n )
F := forest of n rooted trees, each with a single vertex a i with weight w i
while F - tree
Replace the rooted trees T and T’ of least weights from F with w(T) <
w(T’) with a tree T’’ having a new root that has T and T’ as it left and
right children. Label the edge to T as 0 and the edge to T’ as 1.
Assign w(T) + w(T’) to the new tree T’’
{ Huffman encoding tree is complete. }
195
Example: Given {(a,1), (c,2), (t,3)} as (symbol,frequency). What is the Huffman
coding?
Initial forest • (a,1) • (c,2) • (t,3)
Step1 • 3 • (t,3)
0 1
• a • c
Step 2 • 6
0 1
• a •
0 1
• c • t
196

Note: Game trees are another highly studied tree.
Definition (Minimax Strategy): The value of a vertex in a game tree is defined
recursively as:
1. The value of a leaf is the payoff to the first player when the game terminates
in the position represented by this leaf.
2. The value of an internal vertex at an even level is the maximum of the
values of its children. The value of an internal vertex at an odd level is the
inximum of the values of its children.
Theorem: The value of a vertex v of a game tree tells us the payoff to the first
player if both players follow the Minimax strategy and play starts from the
position represented by vertex v.
Notes: Game trees are
• Enormous (not just slightly, but really, really enormous)
• Lead to optimal solutions (if you can compute them)
• Basically intractable using standard computer
197
Note: Tree traversal is extremely important to accessing data. There are many
algorithms, each with a plus and a minus. We will study three traversal
algorithms:
• Preorder
• Inorder
• Postorder
These traversal methods not only are used for data storage, but for representing
arithmetic that is useful for compilers.
Definition: The universal addressing system is defined recursively for an
ordered rooted tree T = (V,E). The root r,V is labeled 0 and its k children are
labeled 1, …, k. For each vertex v,V, labeled A v , its n children are labeled A v .1,
A v .2, …, A v .n.
198

Example: Given a tree T = (V,E) with keys ordered 0 < 1 < 1.1 < 2 < 2.1 < 2.2 <
2.2.1 < 2.3, we represent it as
• 0
• 1 • 2
• 1.1 • 2.1 • 2.2 • 2.3
• 2.2.1
We will use this example for quite some time.
199
Definition (Preorder Traversal): Let T be an ordered rooted tree with root r. If T
consists only of r, then r is the preorder traversal of T. Otherwise, suppose T 1 ,
T 2 , …, T n are subtrees at r from left to right in T. Then the preorder traversal
begins at r and continues by traversing T 1 in preorder, T 2 in preorder, …, and T n
in preorder.
Example: In the tree example at the top of page 199, the preorder traversal order
is 0, 1, 1.1, 2, 2.1, 2.2, 2.2.1, and 2.3.
Definition (Inorder Traversal): Let T be an ordered rooted tree with root r. If T
consists only of r, then r is the inorder traversal of T. Otherwise, suppose T 1 , T 2 ,
…, T n are subtrees at r from left to right in T. Then the inorder traversal begins
by traversing T 1 in inorder, then r, and continues with T 2 in inorder, …, and T n
in inorder.
Example: In the tree example at the top of page 199, the inorder traversal order
is 1.1, 1, 0, 2.1, 2, 2.2.1, 2.2, and 2.3.
200

Definition (Postorder Traversal): Let T be an ordered rooted tree with root r. If T
consists only of r, then r is the postorder traversal of T. Otherwise, suppose T 1 ,
T 2 , …, T n are subtrees at r from left to right in T. Then the postorder traversal
begins by traversing T 1 in postorder, T 2 in postorder, …, T n in postorder, and r.
Example: In the tree example at the top of page 199, the postorder traversal
order is 1.1, 1, 2.1, 2.2.1, 2.2, 2.3, 2, and 0.
Notation: Let add_to_list(v) be a global function to append a vertex v to a list.
The list must be initialized to / at some point before use.
Note: The tree traversal algorithms are all easily defined recursively using a
global list that must be initialized first.
201
procedure preorder_traversal( T: ordered rooted tree )
r := root(T)
add_to_list(r)
for each child c of r from left to right
T(c) := subtree with c as its root
preorder_traversal( T(c) )
procedure inorder_traversal( T: ordered rooted tree )
r := root(T)
if r = leaf then add_to_list(r)
else
q := first child of r from left to right
T(q) := subtree with q as its root
inorder( T(q) )
add_to_list(r)
for each remaining child c of r from left to right
T(c) := subtree with c as its root
inorder_traversal( T(c) )
202

procedure postorder_traversal( T: ordered rooted tree )
r := root(T)
for each child c of r from left to right
T(c) := subtree with c as its root
postorder_traversal( T(c) )
add_to_list(r)
Definition: Logic and arithmetic can be rewritten using binary trees. Using
inorder, preorder, or postorder traversal of the binary tree is known as infix,
prefix, or postfix notation.
Note: The best known is prefix notation, otherwise known as reverse Polish
notation (RPN). This was used in the first pocket sized electronic calculator, the
HP-45 (1972). This notation is valuable in writing compilers, too. See
• http://glow.sourceforge.net/tutorial/lesson7/side_rpn.html
• http://www.hpmuseum.org/rpn.htm
203
Examples: Parentheses disappear completely. It is best to think of a RPN
calculator as a stack machine where data is in the stack and arithmetic operates
on the top elements of the stack.
• The expression 2+3 is written as 2 3 + in RPN.
• The expression [(9+3) * (4/2)] - [(3x) + (2-y)] is written as 9 3 + 4 2 / * 3 x
* 2 y - + - in RPN, where x and y are numbers.
Tree representation: Labels are the operations on internal vertices or the root and
values (constants or simple variables) on the leaves.
Example: 4 * 3 + 2 in RPN is 4 3 * 2 +, or
• +
• * • 2
• 4 • 3
204

Definition: Let G = (V,E) be a simple graph. A spanning tree of G is a subgraph
of G that is a tree containing every vertex in G.
Example: Your instructor wants his town, the states of Connecticut and New
York, and New York City to keep the roads and highways cleared in of ice and
snow connecting his house and Laguardia airport. A graph connecting each of
the relevant endpoints and connecting points can be made. The relevant agencies
can use this graph when deciding how to keep roads open after a storm.
• G • G • G
• PC • PC • PC
• RB • RB • RB
• S • S • S
WB • • LGA WB • • LGA WB • • LGA
205
Theorem: A simple graph G is connected if and only if it has a spanning tree T.
Example: Multicasting over networks.
Note: Constructing a spanning tree can be done in many different ways,
including some very inefficient ones. Two common ways are depth first and
breadth first searches.
Notation: Let visit(v) mean that we keep track of when we first go to vertex v
until we return to v using a backtrack.
procedure visit( G = (V,E): connected graph, T: tree )
for each w,V adjacent to v and not yet in T
add w and edge {v,w} to T
visit(w, T)
206

procedure depth_first( G = (V,E): connected graph )
T := tree with only some single v,V
visit( v, T )
{ T is a spanning tree. }
procedure breadth_first( G = (V,E): connected graph )
T := tree with only some single v,V
L := v
while L - /
Remove first vertex v,L
for each neighbor w,V of v
if w6L and w6T then
Add w to the end of L
Add w and edge {v,w} to T
{ T is a spanning tree. }
207
Theorem: Let G = (V,E) be a connected graph with |V| = n. Then either depth
first or breadth first takes O(e), or O(n 2 ), steps to construct a spanning tree.
Proof: For a simple graph, |E| ; n(n41)/2.
Bactracking applications:
• Graph coloring: can a graph be colored in n colors
• n-Queens problem: find places on a n$n board so n queens are toothless
n
! $
• Sums of subsets: Given " x
# i
% , where xi ,N, find a subset whose sum is M
&i=1
• Web crawlers: search all hyperlinks on a network efficiently
208

Definition: A minimum spanning tree in a connected weighted graph is a
spanning tree that has the smallest possible sum of weights on its edges.
procedure Pim( G = (V,E): weighted connected undirected graph )
T := minimum weighted edge
for i := 1 to |V|42
e := an edge of minimum weight incident to a vertex in T not
forming a simple circuit in T if it is added to T
T := T with e added
{ T is a minimum spanning tree. }
procedure Kruskal(G = (V,E): weighted connected undirected graph )
T := empty graph
for i := 1 to |V|41
e := an edge in G of minimum weight that does not form a simple
circuit in T if it is added to T
T := T with e added
{ T is a minimum spanning tree. }
209
Theorem: The cost of Pim’s algorithm is O(|E|log|V|). The cost of Kruskal’s
algorithm is O(|E|log|E|).
Definition: A graph G = (V,E) is sparse if |E| is very small with respect to |V| 2 .
Comment: Sparse is ill defined intentionally. There are different degrees of
sparseness, too (highly sparse, very sparse, somewhat sparse, hardly sparse, not
sparse, and the Scottish favorite, a wee bit sparse). Matrices can also be
categorized as (fill in the blank type) sparse based on their graphs.
Note: When G is sparse, Kruskal’s algorithm is much less expensive than Pim’s
algorithm.
210

Boolean Algebra
Definition: Let B = { 0, 1 } and B n = B$B$…$B ($ n times). A Boolean
variable x,B. A Boolean function of degree n is a function f: B n %B.
Notation: For x,y,B, define
• x + y = x " y
• x C y = x ! y
• x = ¬x
using the logic predicate notation from the class notes (circa pages 5-6).
Definition: A Boolean algebra is a set B with binary operators " and !, the
unitary operator ¬, elements 0 and 1, and the following laws holding for all
elements of B: identity, complement, associative, commutative, and distributive.
211
Logic gates: Boolean algebra is used to model electronic logic gates, such as
AND, OR, NOT, XAND, XOR, … We design functions with Boolean algebras
and operators. Then we build them using the right gates and wiring patterns.
Typical symbols for AND, OR, and NOT are the following:
AND: OR: NOT:
These are two input AND and OR gates. Versions of these gates exist for more
than two inputs and perform the expected operation on all of the inputs to get
one output.
Definition: A simple output circuit takes the input(s) and has one output. A
multiple output circuit takes input(s) and has multiple outputs.
Example: The gates above are simple output circuits.
212

Examples: Most circuits are of the multiple output variety.
• A half adder adds two bits producing a single bit sum plus a single bit carry:
S := (x"y) ! (¬(x!y)) = x#y and C out := x!y. A half adder has two AND,
one OR, and one NOT gates.
• A full adder computes the complete two bit sum and carry out:
S := (x#y)#c in , where C in is the incoming carry. The carry is quite
complicated: C out := (xCy) + (yCC in ) + (C in Cx). A full adder has two half
adders and an OR gate.
• Ripple adders, lookahead adders, and lookahead carry circuits use many
bits as input to implement integer adders.
Half adder
Full adder
213
Note: Minimizing the Boolean algebra function means a less complicated
circuit. Simpler circuits are cheaper to make, take up less space, and are usually
faster. Add in how many devices are made and there is potentially a lot of
money involved in saving even a small amount of circuitry.
There are two basic methods for simplifying Boolean algebra functions:
• Karnaugh maps (or K-maps) provide a graphical or table driven technique
that works up to about 6 variables before it becomes too complicated.
• The Quine-McCluskey algorithm works with any number of variables.
Going to Google and searching on Karnaugh map software leads to a number of
programs to do some of the work for you.
Definition: A literal of a Boolean variable is its value or its complement. A
minterm of Boolean variables x 1 , x 2 , …, x n is a Boolean product of the {x i
,x i
}.
Note: A minterm is just the product of n literals.
214

Karnaugh maps: The area of a K-map rectangle is determined by the number of
variables (n) and how many (k) are used in a Boolean expression: 2 n4k . Common
arrangements are
• 2 variables: 2$2,
• 3 variables: 4$2, and
• 4 variables: 4$4.
Each variable contributes two possibilities to each possibility of every other
variable in the system. K-maps are organized so that all the possibilities of the
system are arranged in a grid form and between two adjacent boxes only one
variable can change value. Each square in a K-map corresponds to a minterm.
Cover the ones on the map by rectangule that contain a number of boxes equal
to a power of 2 (e.g., 4 boxes in a line, 4 boxes in a square, 8 boxes in a
rectangle, etc.). Once the ones are covered, a term of a sum of products is
produced by finding the variables that do not change throughout the entire
covering, and taking a 1 to mean that variable and a 0 as the complement of that
variable. Doing this for every covering produces a matching function.
215
Given a Boolean function f with inputs x 1 , …, x n , make a table with all possible
inputs and outputs. Then create a K-map with the variables on the left and top
sides of the rectangle. Look for 1’s. The rectangle is a torus, so look for wrap
arounds, too.
Example: f: B 4 %B with a corresponding K-map of
x 1 , x 2
00 01 11 10
00 0 0 1 1
x 3 , 01 0 0 1 1
x 4 11 0 0 0 1
10 0 1 1 1
The K-map is colored to try to find patterns in the Boolean expression that can
be simplified. It is quite common to eliminate some of the Boolean variables
using this approach. Use high quality software if you use the K-map approach.
216

Definition: An implicant is sum term or product term of one or more minterms
in a sum of products. A prime implicant of a function is an implicant that cannot
be covered by a more reduced (i.e., one with fewer literals) implicant.
Note: Suppose f is a Boolean function and P is a product term. Then P is an
implicant of f if f takes the value 1 whenever P takes the value 1. This is
sometimes written as P ; f in the natural ordering of the Boolean algebra.
Quine-McCluskey: This algorithm has two steps:
1. Find all prime implicants of the function.
2. Use those prime implicants in a prime implicant chart to find the essential
prime implicants of the function as well as other prime implicants that are
necessary to cover the function.
The algorithm constructs a table and then simplifies the table. The method leads
to computer implementations for large numbers of variables. Use high quality
software if you use the Quine-McCluskey approach.
217