Math 187 Solutions to Homework 2: Part 2 Radunskaya 4. Give an ...

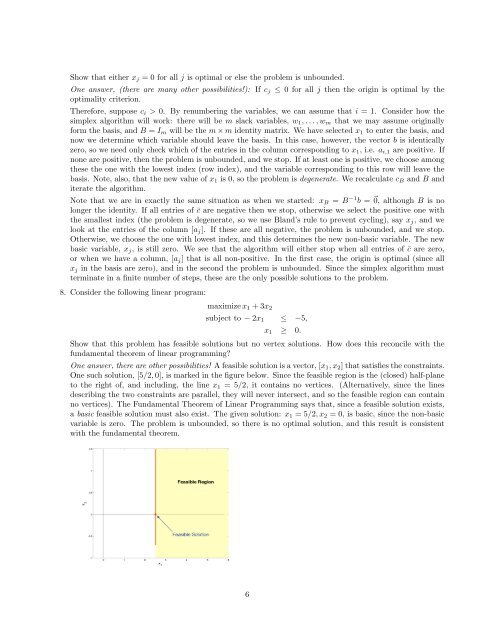
Show that either x j = 0 for all j is optimal or else the problem is unbounded.One answer, (there are many other possibilities!): If c j ≤ 0 for all j then the origin is optimal by theoptimality criterion.Therefore, suppose c i > 0. By renumbering the variables, we can assume that i = 1. Consider how thesimplex algorithm will work: there will be m slack variables, w 1 , . . . , w m that we may assume originallyform the basis, and B = I m will be the m × m identity matrix. We have selected x 1 to enter the basis, andnow we determine which variable should leave the basis. In this case, however, the vector b is identicallyzero, so we need only check which of the entries in the column corresponding to x 1 , i.e. a i,1 are positive. Ifnone are positive, then the problem is unbounded, and we stop. If at least one is positive, we choose amongthese the one with the lowest index (row index), and the variable corresponding to this row will leave thebasis. Note, also, that the new value of x 1 is 0, so the problem is degenerate. We recalculate c B and B anditerate the algorithm.Note that we are in exactly the same situation as when we started: x B = B −1 b = ⃗0, although B is nolonger the identity. If all entries of ¯c are negative then we stop, otherwise we select the positive one withthe smallest index (the problem is degenerate, so we use Bland’s rule to prevent cycling), say x j , and welook at the entries of the column [a j ]. If these are all negative, the problem is unbounded, and we stop.Otherwise, we choose the one with lowest index, and this determines the new non-basic variable. The newbasic variable, x j , is still zero. We see that the algorithm will either stop when all entries of ¯c are zero,or when we have a column, [a j ] that is all non-positive. In the first case, the origin is optimal (since allx j in the basis are zero), and in the second the problem is unbounded. Since the simplex algorithm mustterminate in a finite number of steps, these are the only possible solutions to the problem.8. Consider the following linear program:maximize x 1 + 3x 2subject to − 2x 1 ≤ −5,x 1 ≥ 0.Show that this problem has feasible solutions but no vertex solutions. How does this reconcile with thefundamental theorem of linear programming?One answer, there are other possibilities! A feasible solution is a vector, [x 1 , x 2 ] that satisfies the constraints.One such solution, [5/2, 0], is marked in the figure below. Since the feasible region is the (closed) half-planeto the right of, and including, the line x 1 = 5/2, it contains no vertices. (Alternatively, since the linesdescribing the two constraints are parallel, they will never intersect, and so the feasible region can containno vertices). The Fundamental Theorem of Linear Programming says that, since a feasible solution exists,a basic feasible solution must also exist. The given solution: x 1 = 5/2, x 2 = 0, is basic, since the non-basicvariable is zero. The problem is unbounded, so there is no optimal solution, and this result is consistentwith the fundamental theorem.6