Intensity of Periodic Sound Waves

524 CHAPTER 17 Sound Waves
(a)
(b)
Pressure amplitude
s max
∆P max
s
∆P
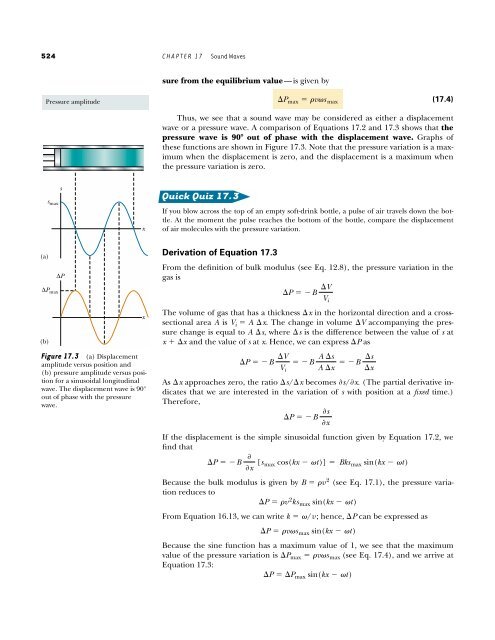
Figure 17.3 (a) Displacement
amplitude versus position and
(b) pressure amplitude versus position
for a sinusoidal longitudinal
wave. The displacement wave is 90°
out of phase with the pressure
wave.
x
x
sure from the equilibrium value—is given by
(17.4)
Thus, we see that a sound wave may be considered as either a displacement
wave or a pressure wave. A comparison of Equations 17.2 and 17.3 shows that the
pressure wave is 90°out of phase with the displacement wave. Graphs of
these functions are shown in Figure 17.3. Note that the pressure variation is a maximum
when the displacement is zero, and the displacement is a maximum when
the pressure variation is zero.
Quick Quiz 17.3
If you blow across the top of an empty soft-drink bottle, a pulse of air travels down the bottle.
At the moment the pulse reaches the bottom of the bottle, compare the displacement
of air molecules with the pressure variation.
Derivation of Equation 17.3
From the definition of bulk modulus (see Eq. 12.8), the pressure variation in the
gas is
�P ��B �V
Vi The volume of gas that has a thickness �x in the horizontal direction and a crosssectional
area A is Vi � A �x. The change in volume �V accompanying the pressure
change is equal to A �s, where �s is the difference between the value of s at
x ��x and the value of s at x. Hence, we can express �P as
�P ��B �V
V i
�P max � �v�s max
��B
A �s
A �x
As �x approaches zero, the ratio �s/�x becomes (The partial derivative indicates
that we are interested in the variation of s with position at a fixed time.)
Therefore,
�P ��B �s
�s/�x.
�x
If the displacement is the simple sinusoidal function given by Equation 17.2, we
find that
�P ��B �
�x [smax cos(kx � �t)] � Bksmax sin(kx � �t)
Because the bulk modulus is given by (see Eq. 17.1), the pressure variation
reduces to
�P � �v
From Equation 16.13, we can write k � �/v ; hence, �P can be expressed as
2 B � �v
ksmax sin(kx � �t)
2
�P � �v�s max sin(kx � �t)
��B �s
�x
Because the sine function has a maximum value of 1, we see that the maximum
value of the pressure variation is �Pmax � �v�smax (see Eq. 17.4), and we arrive at
Equation 17.3:
�P ��Pmax sin(kx � �t)