numerical3j

Recommendations

Info

{10} • Numerical Methods Solution Let f (x) = sin x, so we apply the bisection method to f , starting from [a 0 ,b 0 ] = [3,4]. As f is continuous, f (3) = sin3 ∼ 0.141 is positive, and f (4) = sin4 ∼ −0.757 is negative, so there is a solution in [a 0 ,b 0 ]. We know from trigonometry that sinπ = 0, so x = π is a solution. In fact, π is the only solution for x ∈ [3,4]. So by approximately solving sin x = 0 in [3,4], we approximate π. At the first step, we consider the midpoint 7 2 = 3.5 of [a 0,b 0 ] = [3,4] and compute f ( 7 2) = sin3.5 ∼ −0.351, which is negative. So the sign of f (3), which is positive, is opposite to the sign of f ( 7 2) , which is negative. Hence by the intermediate value theorem, there must be a solution for x ∈ [3, 7 2 ], and we set [a 1,b 1 ] = [ 3, 7 2] = [3,3.5]. At the second step, consider the midpoint 13 4 = 3.25 of [a 1,b 1 ] = [3,3.5]. We compute f ( ) 13 4 = sin3.25 ∼ −0.108, which has opposite sign to f (3), which is positive, and so we set [a 2 ,b 2 ] = [3, 13 4 ] = [3,3.25]. At step 3, consider the midpoint 25 8 = 3.125 of [a 2,b 2 ] = [3,3.25] and compute f ( ) 25 8 = sin3.125 ∼ 0.017, which has opposite sign to f (3.25). So we take [a 3 ,b 3 ] = [ 25 8 , 13 ] 4 = [3.125,3.25]. At step 4, consider 51 16 = 3.1875. We compute f (3.1875) = sin3.1875 ∼ −0.046, which has opposite sign to f (3.125), so [a 4 ,b 4 ] = [ 25 8 , 51 16] = [3.125,3.1875]. At step 5, we compute f ( ) 101 32 = f (3.15625) = sin3.15625 ∼ −0.015, which has opposite sign to f ( 25 8 ) = f (3.125), so [a 5,b 5 ] = [ 25 8 , 101 ] 32 = [3.125,3.15625]. We now know that there is a solution to sin x = 0 in the interval [ 25 8 , 101 ] 32 = [3.125,3.15625], which has length 101 32 − 25 8 = 1 32 = 0.03125. So we know the solution to within 0.03125, which is better than the desired accuracy of 0.05. As you can see, the bisection method can be a rather repetitive and time-consuming process! Because it is an algorithm requiring repeated evaluation of a function, it is well suited to implementation on a computer. We can save ourselves some effort by tabulating the computations. At each stage, we can note down a n and b n and the signs of f (a n ) and f (b n ), then the midpoint a n+b n 2 and the sign of f ( a n+b n 2 ). From this data we can calculate the next interval [a n+1 ,b n+1 ] straightforwardly. This is quicker than writing out each step in English! The previous example could be tabulated as shown below.
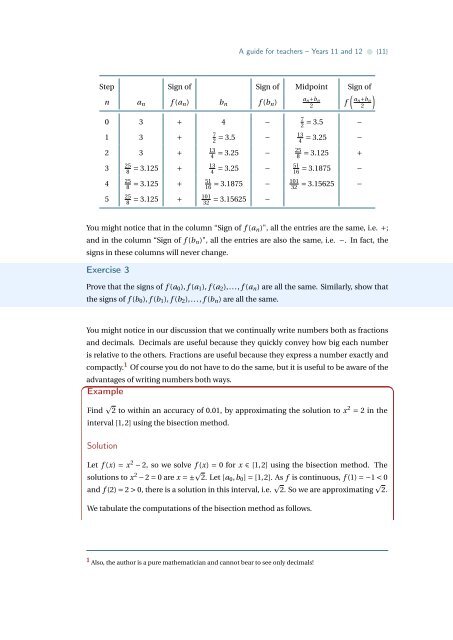
A guide for teachers – Years 11 and 12 • {11} Step Sign of Sign of Midpoint Sign of ) n a n f (a n ) b n f (b n ) 0 3 + 4 − 1 3 + 2 3 + 3 4 5 a n +b n 2 f ( an +b n 2 7 2 = 3.5 − 7 2 = 3.5 − 13 4 = 3.25 − 13 4 = 3.25 − 25 8 = 3.125 + 25 8 = 3.125 + 13 4 = 3.25 − 51 16 = 3.1875 − 25 8 = 3.125 + 51 16 = 3.1875 − 101 32 = 3.15625 − 25 8 = 3.125 + 101 32 = 3.15625 − You might notice that in the column “Sign of f (a n )", all the entries are the same, i.e. +; and in the column “Sign of f (b n )", all the entries are also the same, i.e. −. In fact, the signs in these columns will never change. Exercise 3 Prove that the signs of f (a 0 ), f (a 1 ), f (a 2 ),..., f (a n ) are all the same. Similarly, show that the signs of f (b 0 ), f (b 1 ), f (b 2 ),..., f (b n ) are all the same. You might notice in our discussion that we continually write numbers both as fractions and decimals. Decimals are useful because they quickly convey how big each number is relative to the others. Fractions are useful because they express a number exactly and compactly. 1 Of course you do not have to do the same, but it is useful to be aware of the advantages of writing numbers both ways. Example Find 2 to within an accuracy of 0.01, by approximating the solution to x 2 = 2 in the interval [1,2] using the bisection method. Solution Let f (x) = x 2 − 2, so we solve f (x) = 0 for x ∈ [1,2] using the bisection method. The solutions to x 2 − 2 = 0 are x = ± 2. Let [a 0 ,b 0 ] = [1,2]. As f is continuous, f (1) = −1 < 0 and f (2) = 2 > 0, there is a solution in this interval, i.e. 2. So we are approximating 2. We tabulate the computations of the bisection method as follows. 1 Also, the author is a pure mathematician and cannot bear to see only decimals!
Page 1 and 2: VCAA-AMSI maths modules 348 9012 x
Page 3 and 4: Assumed knowledge . . . . . . . . .
Page 5 and 6: A guide for teachers - Years 11 and
Page 9: A guide for teachers - Years 11 and

numerical3j

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?