x - Didier

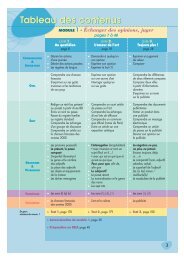
SystèmesLes équations, les systèmesd’équations et les inéquationssont des outils déjàsouvent manipulés.Outre le passage à troisinconnues, une des nouveautésest ici de respecterplusieurs contraintes pouressayer d’optimiser deschoix.Ces contraintes se traduisentsouvent par deséquations et des inéquationsdont on doit tenircompte simultanément.C’est l’objectif de la programmationlinéaire.Les contenusÉquation ax + by + c =0 p.40Inéquation ax + by + c >0 p.42Systèmes linéaires detrois équations à trois inconnues p. 44La fameuse calculatrice de la Faire marque le bon « choix… Calculi »chapitre 2 Systèmes r 37

2 Inéquation ax + by + c >0Le plan est rapporté est rapporté au repère (O ; i , j ).Si a ou b est non nul, l’ensemble des points M(x ; y) tels que ax + by + c > 0 estun demi-plan dont la droite d’équation ax + by + c = 0 est la frontière.L’autre demi-plan est l’ensemble des points M(x ; y) tels que ax + by + c 0 et de la droite frontière d’équation ax + by + c =0.EXEMPLES :• Exemple n° 1 (b =0)Soit E l’ensemble des points M(x ; y) tels quex –2>0.M E revient à dire que son abscisse est supérieureà 2.E est donc formé des points qui se trouvent à droitede la droite d’équation x =2.y1x < 2x > 2O 1x• Exemple n° 2 (a =0)Soit E l’ensemble des points M(x ; y) tels que2y –3 02y – 3 < 0x• Exemple n° 3 (a et b non nuls)Soit E l’ensemble des points M(x ; y) tels que2x +3y –12 02x + 3y – 12 < 0BxRemarque : Lorsqu’il n’est pas sur la frontière, on aintérêt pour distinguer les deux demi-plans, à utiliser lepoint O(0 ; 0) pour lequel les calculs sont particulièrementsimples.O 142 r chapitre 2 Systèmes

2 Régionnement du planÉNONCÉLe plan est rapporté est rapporté au repère (O ; i , j ).1. Montrer que l’ensemble des points M(x ; y) dont les coordonnées vérifient le système d’inéquations0 y 6 est un polygone.{0 x 5x + y 82. Donner les coordonnées de ses sommets.SOLUTION1. La première inéquation signifie que le point M se trouve entre les droites d’équation x =0 etx =5.La partie colorée en vert correspond aux points qui ne conviennent pas.y1O 10 x 5xÉtape 1Lors de la recherche d’un ensemble depoints dont les coordonnées sont solutions de plusieursinéquations, il y a intérêt à colorer ou à hachurer les partiesqui ne conviennent pas, de sorte que la partie restantesoit la partie recherchée.yLa deuxième inéquation signifie que le point M se trouveentre les droites d’équation y =0 ety = 6. Ici aussi nouscolorons en vert les parties qui ne conviennent pas.0 x 50 y 61O 1xÉtape 2yAL’ensemble des points vérifiant x + y 8 est un demi-plan dont lafrontière est la droite d’équation x + y = 8. Cette droite passepar les points A(0 ; 8) et B(8 ; 0).D’autre part le point O fait partie de ce demi-plan puisque 0 + 0 8.Nous colorons donc le demi-plan de frontière qui ne contientpas le point O.Étape 31O 1J0 x 50 y 6x + y 8KBx2. L’ensemble cherché est donc le pentagone OIJKL dont les sommets ont pour coordonnées O(0 ; 0),I(0 ; 6), J(2 ; 6), K(5 ; 3) et L(5 ; 0).En effet les coordonnées de J vérifient y =6 etx + y = 8, donc x = 2. Celles de K vérifient x =5et x + y = 8, donc y =3.chapitre 2 Systèmes r 43

3 Systèmes linéairesde trois équations à trois inconnuesNotationContrairementaux systèmes2 2, nous nedisposons pasen 1 re d’outilpermettant desavoir si unsystème 3 3a une solutionunique.On appelle système linéaire de trois équations à trois inconnues un système de la{ax + by + cz = dforme a'x + b'y + c'z = d ', où a, b, c, d, a', b', c', d ', a", b", c", d " sont desa"x + b"y + c"z = d "constantes données, les inconnues étant x, y et z.Lorsqu’il y en a, les solutions d’un tel système sont des triplets (x ; y ; z).{x +2y – z =2EXEMPLE : Le triplet (1 ; 2 ; 3) est solution du système x + y + z = 6.– x +2z =544 r chapitre 2 SystèmesLes opérations suivantes ne modifient pas les solutions d’un système :• Permuter deux lignes, L1 L3• Multiplier les deux membres d’une équation par un même nombre non nul,L1 L1• Remplacer une ligne par la somme de cette même ligne avec une autre ligne,L1 L1 + L2• Exprimer, à partir d’une équation, l’une des inconnues en fonction des deuxautres et la substituer dans les deux autres équations, SubstitutionEXEMPLES : Attention, les exemples suivants ne constituent pas la seule ni la meilleureméthode de résoudre le système proposé ; leur but est simplement d’illustrer lethéorème.{–2x +2y +9z =29{– x +2z =5• 3x +4y –3z =2 ⇔ –2x +2y +9z =29 L1 L3– x +2z =53x +4y –3z =2Intérêt : Mettre en première position la ligne intéressante pour une future substitution{– x +2z =5{x =2z –5{x =2z –5• –2x +2y +9z =29⇔ –4z +10+2y +9z =29⇔2y +5z =193x +4y –3z =2 6z –15+4y –3z =2 4y +3z =17Intérêt : Les deux dernières équations constituent un système 2 2.{x =2z –5{x =2z –5• 2y +5z =19 ⇔ –4y –10z =–38 L2 – 2 L24y +3z =17 4y +3z =17Intérêt : Dans les deux dernières lignes, les coefficients de y sont opposés et prêts à êtreadditionnés.{x =2z –5• –4y –10z =–38 ⇔4y +3z =17{x =2z –5–4y–10z =–38–7z =–21Intérêt : L’addition des deux dernières lignes permet d’avoir z comme seule inconnuedans la troisième équation.Il ne reste plus, pour terminer la résolution de ce système, qu’à calculer z dans la troisièmeéquation (z = 3), puis y connaissant z dans la deuxième (y = 2) et enfin x connaissantz dans la première (x = 1).Le système a donc pour unique solution le triplet (1 ; 2 ; 3).L3L3 + L2Substitution

3 Résolution par substitutionÉNONCÉSOLUTIONRésoudre, par la méthode de substitution, le systèmeC’est dans la deuxième équation qu’il est le plus facile d’exprimer une inconnue, à savoir y, en fonctiondes deux autres.{2x +5y +4z =3{y =–3x +2z –2L2 L13x + y –2z = –2 ⇔ 2x + 5(– 3x +2z –2)+4z = 3 substitution5x +2y +3z =–3 5x + 2(– 3x +2z –2)+3z =–3 substitution⇔⇔⇔{y =–3x +2z –2–13x +14z = 13– x +7z =1{y =–3x +2z –2x= 7z –1– 13(7z –1)+14z =13{y =–3x +2z –2x = 7z –1–77z =0Le triplet (– 1 ; 1 ; 0) est donc l’unique triplet solution du système proposé.⇔{z =0x= –1.y =1{2x +5y +3z =33x + y –2z =–2 .5x +2y +3z =–3On peut exprimer x en fonction de z dans la3 e équation et le substituer dans la deuxième.Lorsque l’un descoefficients de x, y ou z est égal à1 ou – 1, la substitution donnedes calculs simples.4 Méthode par combinaisons linéaires{2x –3y +2z = –6 (L1)ÉNONCÉ On considère le système (S) 4x +5y –4z = 18 . (L2)–12x +2y +5z = – 13 (L3)1. Quelle équation (E1) obtient-on en faisant l’opération L2 – 2L1 ?2. Quelle équation (E2) obtient-on en faisant l’opération L3 + 3 L2 ?3. Quelles valeurs donner à a et b pour que l’opération a E1 – b E2 élimine les z ?4. Terminer la résolution du système en n’oubliant pas de vérifier que le triplet trouvé est biensolution du système.SOLUTION1. On obtient (4x +5y –4z) – 2(2x –3y +2z) = 18 – (– 6), doncl’équation (E1) est 11y –8z = 30.Ici on commence2. On obtient (– 12x +2y +5z) + 3(4x +5y –4z)=–13+3 18 par éliminer l’une des troisdonc l’équation (E2) est 17y –7z = 41.inconnues en combinant deux3. L’opération 7 E1–8 E2 donneéquations une première fois, puis7(11y –8z) – 8(17y –7z) =7 30–8 41, soit – 59y = – 118.deux autres équations unedeuxième fois.4. On a donc y = 2 ; en reportant cette valeur dans (E2), on Cette méthode nécessite la vérificationque le triplet trouvé estobtient – 7z = 7, donc z =–1.En substituant ces deux valeurs dans (L3) par exemple, on obtient bien solution.2x = 2, donc x =1.Si le système a une solution, cette solution est forcément le triplet (1 ; 2 ; – 1).Vérification : 2x –3y +2z =2 1–3 2+2 (– 1) = – 6 ; le triplet vérifie donc (L1).On vérifie de même qu’il vérifie (L2) et (L3).chapitre 2 Systèmes r 45

1. PavageObjectif : Résoudre des problèmes d’aires à l’aide de systèmes.AConfiguration n °1Dans cette partie, on se propose de calculer l’aire de la surfacecoloriée en rouge sur la figure ci-contre où ABCD est un carréde côté 1 et où I, J, K et L sont les milieux des côtés.AIBLJDKC1. On admet que les surfaces colorées de la même couleur ontla même aire.On désigne par a l’aire de la surface rouge (cette forme est en faitun carré), par b celle de chaque trapèze jaune et par c celle dechaque triangle bleu.a. Établir une relation entre a, b et c exprimant que la somme desaires colorées est égale à l’aire du grand carré.cbbcacbbcb. Quelle portion du grand carré représente l’aire coloréeci-contre ?En déduire une relation entre b et c.bcbcacbbcc. En observant le découpage de la surface jaune, établir unedeuxième relation entre b et c.2. Déterminer a, b et c en résolvant le système formé par les trois relations précédentes.46 r chapitre 2 Systèmes

B Deuxième configurationLes hypothèses étant les mêmes que pour la première configuration,on se propose ici d’évaluer l’aire de la surface colorée qui est en faitun octogone régulier.1. On admet encore que, par la suite, les surfaces colorées de la même couleur ont la même aire.a. Établir une relation entre x, y, z, t et u exprimantque la somme des aires colorées est égaleà l’aire du grand carré.b. En utilisant la figure ci-dessous et la valeurde a trouvée dans la partie A, établir une relationentre x et y.tzttztttzuyyutyyxzyyuyyutzttttzuyyutyyxzyyuyyutzttc. Quelle portion de l’octogone représente letriangle OBC ? (O est le centre du carré)Vérifier que les triangles ABC et OBC ont unebase de même longueur et une hauteur commune.En déduire que z – 2+ y = x – 8.d. Quelle portion du grand carré représentel’aire colorée ?En déduire une relation entre z et t.En remarquant que t = c (voir partie A), calculerz.AtztCOBttzuyyutyyxzyyuyyutzttx +8y +4u = 1 – 22. a. Montrer que x, y et u sont solutions du système (S){x +4y = 1 – . 5y = x – – — 1 8 80b. Terminer la résolution de ce système et en déduire l’aire demandée.chapitre 2 Systèmes r 47

2. Optimisation d’un atelierObjectif : Résoudre un problème de programmation linéaire.Un atelier de confection fabrique en série deux modèles de chemises de luxe.Une chemise du modèle A nécessite 1 mètre de tissu, 4 heures de travail et rapporte 5 euros.Une chemise du modèle B exige 1,5 mètre de tissu, 2 heures de travail et rapporte 3 euros.On suppose que l’atelier dispose quotidiennement de 150 mètres de tissu et de 400 heures detravail. On suppose également que toute la production est écoulée.On note x et y les nombres respectifs de chemises du modèle A et du modèle B, fabriquées parjour.A Préambule au problème1. a. On suppose dans cette question que x = 30 et y = 50.Calculer la quantité de tissu nécessaire, le nombre d’heures utilisées et le bénéfice réalisé.b. Les situations suivantes sont-elles possibles ? Justifier la réponse.• x = 60 et y =80;• x = 80 et y = 40.2. Exprimer en fonction de x et y :• la quantité de tissu utilisée ;• le nombre d’heures employées ;• le bénéfice réalisé.3. Quel est le bénéfice réalisé si l’on a utilisé 70 mètres de tissu et 160 heures de travail ?BPolygone des contraintesLe plan est rapporté au repère orthonormé (O ; i, j ), 1 centimètre représentant 10 mètres en abscisseset 10 heures en ordonnées.La situation où x et y sont les nombres respectifs de chemises du modèle A et du modèle B fabriquéespar jour, est représentée par le point de coordonnées (x ; y).1. Placer les points A(30 ; 50), B(60 ; 80) et C(80 ; 40) correspondant aux trois situationsdécrites au A1.2. Justifier que le point de coordonnées (x ; y) correspond à une situation possible si ses coordonnées{x 0 et y 0vérifient le système 2x +3y 300.2x + y 200L’ensemble des points vérifiant ce système est appelé le polygone des contraintes.3. Parmi les points A, B et C, quels sont ceux qui font partie du polygone des contraintes ?CConstruction du polygone des contraintes1. Représenter les droites 1 et 2 d’équations respectives 2x +3y = 300 et 2x + y = 200.Indication : Commencer par déterminer les points d’intersection de 1 et 2 avec les axes du repère.2. Représenter le polygone des contraintes.Indication : On éliminera de préférence les parties qui ne conviennent pas, comme à la page 43.3. Vérifier que ce graphique confirme les résultats de la question B3.48 r chapitre 2 Systèmes

D ConclusionL’objectif est de déterminer la production qui rend maximum le bénéfice.1. a. Montrer que les points de coordonnées (x ; y) correspondant à une situation telle que le bénéficesoit de 300 euros, se trouvent sur une droite ∆ dont on donnera une équation.b. Déterminer les coordonnées de deux points E et F de ∆ d’abscisses respectives 30 et 48 faisantpartie du polygone des contraintes. Représenter ∆ sur le graphique précédent.2. Recommencer avec un bénéfice de 400 euros.On obtiendra deux points E ' et F ' d’abscisses respectives 38 et 50 ainsi qu’une droite ∆'.a. Représenter ces divers éléments.b. Quelle est la position relative des droites ∆ et ∆' ? Justifier.c. Pourquoi les points E ' et F' sont-ils « meilleurs » pour notre objectif que E et F ?d. Peut-on faire encore mieux ? Comment ?e. De quel système le couple (x ; y) qui rend le bénéfice maximum est-il solution ? Résoudre lesystème et en déduire le bénéfice maximum.EApplicationRecommencer la partie D lorsque :a. une chemise du modèle A rapporte 5 euros, une du modèle B rapporte 2 euros ;b. une chemise du modèle A rapporte 2,40 euros, une du modèle B rapporte 6 euros.FAvec le logiciel GeoplanW1. Préparation de la feuille• Ouvrir une Nouvelle figure du plan et faire Afficher le repère prédéfini .• Ouvrir la boîte de styles et faire Afficher les graduations en cliquant sur , puis sur undes axes du repère.• Cliquer sur plusieurs fois afin qu’apparaissent les graduations 200 sur les deux axes.Vouspouvez déplacer l’origine du repère avec le bouton droit de la souris.2. Polygone des contraintes• Créer, Demi-plan, Défini par une inéquation. Entrer dans la boîte de dialogue l’inéquation X

3. Programmation linéaire avec tableurObjectif : Fournir un outil de vérification simple pour tout problème de programmation linéaire.Nous reprenons ici des éléments du TD n ° 2.Il y a été établi que le polygone des contraintes était défini par{x 0 et y 02x +3y 300.2x + y 2001. La quantité à optimiser est le bénéfice donné par l’expression 5x +3y.• Ouvrir une nouvelle feuille de votre tableur et préparer la page suivante :Indication : Les valeurs de x et y sont données au hasard dans les cellules A3 et B3, le contenu des cellules C3, D3et E3 est obtenu en entrant les formules adéquates.• Ouvrir le solveur du tableur par Outils, Solveur et compléter les différentes cellules en suivantles explications ci-dessous :Indication : La cellule cible est la cellule où apparaîtra le bénéfice maximum.• Cocher la case Max caron recherche un maximum.Indication : Les cellules variablessont les cellules contenant lesvaleurs de x et y.• Pour entrer une descontraintes du problème,cliquer sur Ajouter et compléterles différentes cases.• Cliquer sur la case Résoudre. La solution apparaît alors dans la cellule cible et on peut lire égalementles valeurs de x et y qui réalisent ce maximum.2. Utiliser ce procédé pour vérifier les divers résultats de l’application du TD n° 2.Vous pourrez l’utiliser également pour vérifier les résultats des exercices de programmationlinéaire que vous rencontrerez dans ce chapitre.50 r chapitre 2 Systèmes

4. Myrtille, fraise et abricotObjectif : Présenter une situation concrète conduisant à résoudre un système 3 3.Pour satisfaire la gourmandise de ses petits enfants, Mylène a préparé de la confiture.Elle a placé les pots, petits, moyens et grands sur trois étagères. Or il y a 3 kilogrammes de confituresur chaque étagère.On veut déterminer la masse en grammes d’un grand pot, d’un pot moyen et d’un petit pot.FraiseAbricotFraiseMyrtilleFraiseAbricotMyrtilleMyrtilleFraiseAbricotFraiseMyrtilleFraiseAbricotFraiseAbricotFraiseMyrtilleFraiseAbricotMyrtilleMyrtilleFraiseFraise1. Désignant par x, y et z les masses respectives, en kilogrammes, des pots grands, moyens etpetits, écrire un système de trois équations à trois inconnues dont le triplet (x ; y ; z) est solution.2. Résoudre ce système.3. Déterminer la quantité (en kilogrammes) de chacune des sortes de confiture.5. ÉnigmeObjectif :Travailler sur les lignes d’un système.Sachant que toutes les balles de la même couleur ont la même masse, déterminer la masse quiéquilibre la troisième balance.2,3 kg 1,8 kg?chapitre 2 Systèmes r 51

Forme ax + by + c =0Dans les exercices 1 à 4, le plan est rapporté à un repère(O ; i, j ).1 Recopier et compléter le tableau suivant qui propose deuxéquations de trois droites non parallèles à l’axe (O ; j ).Droite 1 2 3Équationdu type y =2x –4y = mx + pÉquationdu type 3x –5y =1 4x +5y =10ax + by = c2 On a représenté trois droites dont les équations sont les suivantes: 1 : x +2y =6, 2 :2x + y =6, 3 :3x –4y = 12,ainsi qu’une quatrième droite 4 .Reconnaître la couleur de chacune des droites et déterminer uneéquation de 4 sous la forme ax + by = c.8 Dans chacun des cas, dire si les droites 1 et 2 sont sécantes,strictement parallèles ou confondues.Représenter les deux droites.Lorsqu’elles sont sécantes, conjecturer graphiquement les coordonnéesdu point d’intersection, puis vérifier par le calcul.a. 1 : x –2y =5; 2 :–2x +4y = 10.b. 1 :3x –5y =13; 2 :5x +8y = – 11.c. 1 : – x + – y =1; 3 2 2 :2x +3y =6.Systèmes linéaires dedeux équations à deux inconnuesPour les exercices 9 à 18, résoudre le système, puis contrôler graphiquementle résultat, soit en traçant les deux droites dans unrepère, soit en utilisant l’écran graphique d’une calculatrice.92x +3y =7.{ –3x +2y =–410x – y =5.{ 2x +3y =11110,5x + 1,2y =5{.3x + 0,2y =1312y – x = 1,4.{ 2x +5y =3j1350x + 100y = 400.{ 200x – 300y = – 50014y – x =2.{ y + x =3O i15{– x+ – y =3 3 2 .x –3y =016{3 –4 x + 2 – y =5 3x –2 –– y .=1 33 Soit la droite d’équation 2x +3y =1.1. Soit A le point de d’abscisse – 1.Déterminer son ordonnée.2. Soit B le point de d’ordonnée 3.Déterminer son abscisse.3. Représenter la droite .4 Soit la droite d’équation 3x –2y =6.1. Déterminer les coordonnées du point d’intersection de avecl’axe des abscisses.2. Déterminer les coordonnées du point d’intersection de avecl’axe des ordonnées.3. Représenter la droite .Pour les exercices 5 à 7, représenter la droite donnée par unede ses équations.5a. : x –5y =7; b. :4x –3y +7=0.17Dans les exercices 19 à 22, résoudre le système en le mettantd’abord sous la forme d’un système linéaire de deux équations àdeux inconnues.1920212x +3y =4.{ 5x –7y =9{y– =2 xx +2y =5.{y +1— =1 x –12x –3y =5.{– 1+ 2 – =0 x yx + y =1.18–2x +5y =0{ 3x –7y =0.67a. :3x +2=0; b. :2y +5=0.a. : x – 2+ y – 3=1; b. : 0,2x + 0,6y =1.22{x +1— = — x –1y –1 y +2x – y =4.52r chapitre 2 Systèmes

232x +3y =13On considère le système (S) :{.3 x – y =31. Pourquoi ce système n’est-il pas linéaire ?2. Remplacer x par X et y par Y dans (S).Le système (S') obtenu est-il linéaire ?3. Résoudre le système (S'), puis en déduire les solutions éventuellesdu système (S).24On considère le système (S) :{5–x + – 7 =–11 y1 –x – 3 – =11 y1. Quels changements de variables faut-il utiliser pour transformer(S) en un système linéaire (S') ?2. Résoudre le système (S'), puis en déduire les solutions éventuellesdu système (S).{— 2+ y 2 =625 Résoudre x +3.—–5+2y 2 =3.x +3Problèmes se ramenantà la résolution d’un système 2 226 Trouver deux nombres dont la somme est 253 et la différence125.27 Pour l’achat de trois croissants et de six baguettes, Jean apayé 5,55 euros.Chez le même boulanger, Jeanne a payé 5,60 euros pour l’achatde cinq baguettes et quatre croissants.Quel est le prix d’une baguette et quel est celui d’un croissant ?28 Déterminer un nombre de deux chiffres tel que la somme deses deux chiffres est 12 et si on permute ses deux chiffres, lenombre augmente de 36.29 Trouver deux nombres dont la somme est 39 et dont la différencedes carrés est 429.30 Le périmètre de ce champ est de 100 mètres. Si l’on augmentela longueur de 5 mètres et si on diminue la largeurde 3 mètres, son aire diminue de 21 m 2 .Quelles sont les dimensions de ce champ ?31 Dans ce cinéma de banlieue, si on augmente le prix habitueldes places de 1 euro, le nombre de spectateurs diminue de 150et la recette diminue de 600 euros.Si on diminue le prix habituel des places de 1 euro, le nombrede spectateurs augmente de 50 mais la recette diminuede 200 euros.Quel est le prix habituel des places ?.32 Dans une classe de 30 élèves, il y a :• cinq élèves qui font partie à la fois du club photo et du clubaéronautique ;• huit élèves qui ne font partie d’aucun de ces deux clubs ;• deux fois plus d’élèves dans le club photo que dans le clubaéronautique.Quel est le nombre d’élèves ayant choisi :a. uniquement le club photo ?b. uniquement le club aéronautique ?Régionnement du planDans les exercices 33 et 34, le plan est rapporté à unrepère (O ; i , j ).33 1. Représenter la droite d’équation 2x +3y =5.2. Le point A(1 ; 2) fait-il partie du demi-plan d’équation2x +3y >5?3. Colorier le demi-plan d’équation 2x +3y >5.34 1. Représenter les droites d’équations x +2y =10et 4x + y =8.2. Le point A(3 ; 1) fait-il partie du demi-plan d’équationx +2y < 10 ? et du demi-plan d’équation 4x + y

40302048{x +3y –5z =92x –2y –3z=3.– x +3y + z =149{2x +3y –5z =–24x +2y –3z =2 .–2x +5y +2z =1210O 10 2050{2x + y + z =5x –2y – z =–5 .3x + y –2z =–251{3x +5y +2z =192x +5y +3z = 21.5x +5y –4z =341302010Problèmes se ramenantà la résolution d’un système 3 3O 10 2052 En réunissant l’argent de leurs tirelires, Céline et Violetteont 350 euros,Violette et Pauline ont 380 euros, Pauline et Célineont 450 euros.42300Ont-elles assez d’argent à elles trois pour faire un cadeau quicoûte 600 euros ?20010053 À la fin de la partie,Alceste avait autant de billes que Nicolaset Agnan réunis, Nicolas avait 12 billes de moins qu’Alceste et6 billes de plus que Agnan.Mais combien de billes avaient-ils à eux trois ?43O 100 200 300B(2;3)1A(1;1)O 1C(4;2)54 Une compagnie aérienne pratique trois tarifs différents pourle trajet Paris-Athènes :• le tarif A pour les enfants de moins de 8 ans ;• le tarif B pour les enfants entre 8 et 16 ans ;• le tarif C pour les personnes de plus de 16 ans.La famille Lenoir, formée d’un couple d’adultes, et de trois enfantsde 4, 6 et 14 ans a payé 730 euros pour ce voyage.La famille Legris, formée des deux parents et de cinq enfantsâgés respectivement de 4, 5, 10, 12 et 17 ans a payé 1110 euros.La famille Leblanc, où la mère se déplace avec deux enfants de 2et 10 ans, a payé 450 euros.Calculer le prix du billet d’avion pour chacun des trois tarifs.Systèmes linéaires detrois équations à trois inconnuesPour les exercices 44 à 51, résoudre les systèmes.{2x +3y –5z =044 2y –3z = –1 .12z =12{2x +3y –5z =145 2y –3z = – 2 .y + z =455 Au cours du trimestre, José a eu successivement 8, 12et 16 aux contrôles de mathématiques.Aux mêmes contrôles Victoire a eu 12, 16 et 8.Le professeur a annoncé qu’il avait appliqué différents coefficients.Il n’a pas précisé lesquels mais a dit que leur somme estégale à 8.Sachant que José et Victoire ont eu respectivement 14 et 10,5de moyenne, retrouver les coefficients appliqués à chacun desdevoirs.46{x + z =6y + z =8 .x + y =447{2x +3y =–12y –3z =–2 .3x +5z =356 Les côtés d’un triangle sont proportionnels aux nombres 3,4 et 5. Le périmètre de ce triangle est 132 mètres.Calculer les longueurs des côtés du triangle.54 r chapitre 2 Systèmes

57 À l’école de danse, les 48 élèves sont répartis dans troiscours : hip-hop (25 élèves), modern jazz (18 élèves) et classique(22 élèves).Trois d’entre eux participent aux trois cours, cinq ont choisi uniquementmodern jazz et quatre ont pris à la fois classiqueet modern jazz mais pas hip hop.Combien d’élèves ont choisi de suivre classique et hip-hop maispas modern jazz ?Indication : On pourra s’aider du schéma suivant.HHxMJ61 Jacques, Alain et Jean Marc se rendent chez le même fleuristeafin d’offrir chacun un bouquet à Virginie.Avec 3 roses, 5 gerberas et 7 tulipes, Jacques a payé 21,40 euros.Avec 5 roses, 4 gerberas et 6 tulipes, Alain a payé 22,40 euros.Avec 4 roses, 6 gerberas et 5 tulipes, Jean Marc a payé 21,30 euros.Combien aurait payé Bernard pour un bouquet composé de5 roses, 5 gerberas et 5 tulipes ?62 Pour faire ses constructions, Yann utilise des pavés identiques,les faces ayant les mêmes dimensions étant de la mêmecouleur.En observant la figure ci-dessous, déterminer les dimensions dechacun des pavés.yzC9,1 cm58 Sur une photographie prise au zoo de Vincennes, on aperçoit15 têtes, 10 bosses et 44 pattes.Quel est le nombre de chameaux, de dromadaires et d’autruchesphotographiés ?Indication : Seules ces trois espèces d’animaux figurent sur la photographie.7,2 cm6,9 cm59 Sur la figure ci-dessous, on a représenté un triangle ABCavec son cercle inscrit.On donne AB = 7 cm, BC = 7,6 cm, AC = 9 cm et on pose AI = x,BJ = y et CK = z.Calculer x, y et z.B63 L’expression de la fonction représentée ci-dessous est de laforme ƒ(x)=ax 2 + bx + c.Déterminer les réels a, b et c pour que la courbe passe par lespoints A, B et C dont les coordonnées sont indiquées sur le graphique.A(–2;7)IJOAKC1O 1C(6;–1)60 « Si je perdais 5 % de ton poids et si tu gagnais 10 % dumien, nous aurions le même poids et nous pèserions à nous deux,4 kilogrammes de plus que maintenant. »Quel est le poids de ces deux individus ?B(2;–5)chapitre 2 Systèmes r 55

Ce que je dois savoir■ L’équationd’une droite sousla formeax + by + c =0,a ≠ 0 ou b ≠ 0(p. 40)■ Le parallélismede deux droites : ax + by + c =0et ' :a'x + b'y + c' =0(p. 40)■ Le déterminantd’un systèmelinéaire de2 équations à2 inconnues(p. 40)■ L’inéquationd’un demi-plan(p. 42)Ce que je dois savoir faireRésoudre un Interpréter Représenter un Interprétersystème linéaire graphiquement la demi-plan défini graphiquement un2 2 par solution d’un par une inéquation système linéairesubstitution ou système linéaire(p. 42)d’inéquationscombinaison2 2(p. 43)(p. 41)(p. 41)Résoudre unproblèmed’optimisation(pp. 48 et 49)Qui a raison ?■ Les opérationsqui ne changentpas les solutionsd’un système(p. 44)Résoudre unsystème 3 3 parsubstitution oucombinaison(pp. 44 et 45)

Choisir la (ou les) affirmation(s) juste(s)Pour vérifier vos résultats, voir en fin de manuel.A B C1jOiUne équation de la droite est y = – 1,5x +3 3x –2y –6=0 6x +4y =12x – 2y + 5 = 02jOiALes coordonnées (x ; y) du point A vérifient x –2y +5>0 x –2y +5=0 x –2y +50{est colorée envert gris jaunex –2y +5

64 Carré magique69 Énigme{3♣ + 4♥ + 5♠ = 702♣ + 5♥ + 7♠ = 81Résoudre l’énigme suivante :5♣ + 2♥ + 5♠ = 60♣ + ♥ + ♠ = ?Un carré magique est un tableau de nombrestels que la somme des nombres dans 7 x t58 r chapitre 2 Systèmesune ligne, une colonne ou une diagonaleest la même.y 8 41. Montrer que si le tableau ci-contre estun carré magique, alors x + t +7=S, 5 10 zoù S désigne la somme commune dechaque ligne.2. Écrire quatre autres équations à partir du tableau et en déduireun système linéaire de quatre équations à quatre inconnues x,y, z, t.3. Trouver alors les valeurs de x, y, z et t et vérifier que le tableauest bien un carré magique.65 Tétraèdre magiqueUn tétraèdre est ditmagique si la somme desxnombres de chaque faceest la même.1. En supposant que lasomme commune desnombres de chaque faceest égale à 12, écrire quatreyéquations liant les zvariables x, y, z, t.2. Résoudre le systèmeformé par ces équations.t66 Promenons-nous dans les bois…Pour aller chez mère-grand, le Petit Chaperon rouge, encombré parson panier plein de victuailles, a marché 1km/h moins vite qued’habitude et a mis 6 minutes de plus.Au retour, en s’échappant, il a couru 4 km/h plus vite que d’habitudeet a mis 12 minutes de moins.Quelle est la distance séparant la maison du Petit ChaperonRouge de celle de mère-grand ?Indication : 6 minutes = 0,1 heure.67 L’union fait la forceUn jardinier met 5 heures pour bêcher son jardin. Son voisin met3 heures pour bêcher le même jardin.Quel temps mettraient-ils s’ils bêchaient ce jardin à deux ?68 Code secretLa combinaison secrète de ce cadenas est un nombre de troischiffres.Le nombre formé par les deux chiffres de gauche est le double decelui formé par les deux chiffres de droite.La somme des trois chiffres est 13.Si l’on permute les chiffres des unités et des centaines, le nombreaugmente de 99.Quel est le code ?70Maximum-minimumOn a représenté ci-dessous le polygone des contraintes, correspondantà une fabrication de deux sortes d’objets A et B. Tousles objets fabriqués sont vendus.Pour x objets A et y objets B fabriqués, le prix de revient s’exprime(en milliers d’euros) par R =3x +5y et le prix de ventepar V =5x +6y.On a représenté également les droites d’équation 3x +5y =27et 5x +6y = 38 correspondant à une production de quatre objets Aet trois objets B.1. Trouver le couple (x ; y ) qui rend le prix de revient minimum.2. Trouver le couple (x ; y ) qui rend le prix de vente maximum.3. Exprimer le bénéfice en fonction de x et y, puis trouver lecouple (x ; y ) qui rend le bénéfice maximum.71jO iC(2;3)D(2;5)Jeu de rôleI(4;3)G(4;2)E(5;5)F(7;3)5x + 6y = 383x +5y = 27Dans ce jeu, vous disposez de deux dés à 20 faces numérotéesde 1 à 20. L’un de ces dés est bleu, l’autre rouge. Jetez les dés.Votre capital santé est donné par le dé bleu. S’il est inférieur à 5,vous êtes éliminé.Votre capital confiance est donné par le dé rouge. S’il est supérieurà 15, vous êtes éliminé.On obtient le capital maléfice en ajoutant le double du nombredu dé bleu et le triple du nombre du dé rouge. Si ce capital estsupérieur à 71, vous êtes éliminé.On obtient enfin le capital courage en retranchant du double dunombre du dé bleu, le triple du nombre du dé rouge. Si ce capitalest supérieur à – 7 vous êtes éliminé.On désigne par x le résultat du dé bleu et par y celui du dé rouge.Le plan est rapporté à un repère (O ; i , j ) dans lequel l’unitéest de 0,5 centimètre sur chaque axe.1. Représentez l’ensemble de tous les points M(x ; y) qui permettentde ne pas être éliminé.2. Si vous êtes éliminé vous ne marquez rien, sinon le résultatde la partie est la somme des quatre capitaux.Quel est le plus grand résultat que l’on puisse obtenir en unepartie ?

72QCMOn a décidé d’acheter pour fleurir un parc, au minimum1200 jacinthes, 3200 tulipes, 3000 narcisses.Deux pépiniéristes proposent :• L’un le lot A, soit 30 jacinthes, 40 tulipes et 30 narcisses pour12 euros.• L’autre le lot B, soit 10 jacinthes, 40 tulipes et 50 narcisses pour10 euros.Le but de l’exercice est de déterminer le nombre x de lots A et lenombre y de lots B que l’on doit acheter pour que la dépensesoit minimale.1. Parmi les couples (x ; y) suivants, lequel permet de fleurir leparc ?a. (10 ; 80) ; b. (40 ; 40) ; c. (30 ; 45).2. Parmi les systèmes suivants, lequel traduit les contraintes dece problème ?{x et y {x et y a. 3x + y 120b. 3x + y 120;x + y 80.x + y 803x +5y 3003x +5y 3003. Parmi les trois zones colorées du schéma suivant laquelle estsusceptible de représenter les contraintes du problème ?5. Parmi les points A, B, C, D, E, lequel est susceptible de correspondreau coût minimal ?20ACB3x + y = 120O 20Dx + y = 803x + 5y = 3006. Lequel des nombres suivants est égal au coût minimal souhaité?a. 900 ; b. 650 ; c. 840 ; d. 0.EZONE 120ZONE 3 ZONE 2O 203x + 5y = 3003x + y = 120 x + y = 804. Parmi les trois droites 1 , 2 et 3 représentées ci-dessousen pointillés, laquelle correspond à un coût de 1100 euros ?Indication : Chercher une équation de cette droite.20 3O 203x + y = 120M (50;50) 1 2x + y = 803x + 5y = 30073À moindre coûtUn directeur de parc animalier veut nourrir ses animaux au moindrecoût en leur apportant cependant un minimum journalierde 120 kilogrammes de protides, 90 kilogrammes de lipides et60 kilogrammes de glucides. Deux aliments tout préparés A et Blui sont présentés sur le marché. Leurs caractéristiques pour unsac sont indiquées dans le tableau :Protides Lipides Glucides PrixSac A 3kg 3kg 1kg 2€Sac B 2kg 1kg 2kg 1€On se propose de déterminer le nombre x de sacs A et le nombre yde sacs B que le directeur doit acheter chaque jour pour que lesbesoins en nourriture soient satisfaits et cela avec un coût minimum.1. Vérifier que les contraintes sont traduites par le système{x 0 et y 03x +2y 120(S).3x + y 90x +2y 602. À tout couple (x ; y) on associe le point M(x ; y) dans un repère(O ; i , j ) où 1 centimètre représente 10 sacs sur chaque axe.a. Parmi les couples suivants, lequel ou lesquels vérifient lescontraintes :• (30 ; 20) ? • (40 ; 10) ? • (10 ; 50) ?b. Déterminer graphiquement la région du plan contenant lespoints M dont les coordonnées vérifient le système (S).3. a. Exprimer en fonction de x et y le coût occasionné par l’achatde x sacs A et y sacs B.b. Déterminer le couple (x ; y) qui rend ce coût minimum.chapitre 2 Systèmes r 59

74 Bracelets de luxeUn artisan joaillier doit fabriquer pour une bijouterie des braceletsor et argent de deux types A et B.Les consignes de fabrication sont les suivantes :• chaque bracelet doit contenir 10 grammes d’or ;• un bracelet de type A doit en outre contenir 20 grammesd’argent et être décoré de 10 éclats de diamant ;• un bracelet de type B nécessite par ailleurs 50 grammesd’argent et 40 éclats de diamant.Pour cet ouvrage, le joaillier reçoit 207 grammes d’or, 600 grammesd’argent et 450 éclats de diamant.Les délais qui lui sont imposés font qu’il ne dispose que de46 heures de travail.1. Sachant qu’un bracelet de type A lui demande 3 heures detravail et un bracelet de type B, 2 heures, écrire l’ensemble descontraintes de fabrication sous forme d’un système d’inéquations.Aide : On désigne par x et y les nombres entiers respectifs de bracelets Aet B fabriqués.Représenter graphiquement ces contraintes (unité sur chaqueaxe : 0,5 centimètre).2. Le travail de l’artisan est rémunéré de la façon suivante :40 euros pour la fabrication d’un bracelet de type A et 54 eurospour celle d’un bracelet de type B. Il doit justifier l’emploi de lamatière première et rendre celle qui n’est pas utilisée.a. Quel nombre de bracelets de chaque type doit-il fabriquerpour obtenir le meilleur salaire ?b. À combien s’élève alors son salaire horaire ?c. Quelle matière première doit-il rendre ?Et en quelle quantité ?75RestructurationUne entreprise emploie au 1 er janvier 5400 employés répartis entrois catégories de personnel : A, B et C.Le responsable du personnel souhaite restructurer l'entreprise,à effectif global constant.Il affirme : « Si on diminue dans l’année les effectifs des catégoriesA et B respectivement de 1 % et de 4 %, et que l’on augmentel’effectif de la catégorie C de 12 %, l’entreprise conserverale même nombre global d’employés. »Son adjoint affirme quant à lui : « On pourrait diminuer les effectifsdes catégories A et B respectivement de 1 % et de 1,5 % etaugmenter l’effectif de la catégorie C de 6 % : l’entreprise conserveraitle même nombre global d’employés. »Sachant qu’aucun ne se trompe dans ses calculs, déterminer larépartition initiale du nombre d’employés par catégories.76 Glaces exotiquesDans une cafétéria, on sert deux sortes de desserts glacés, à basede cocktail exotique, de glace et de fruits confits : la coupe créoleet la coupe tropicale. La confection d’une coupe créole nécessite8 centilitres de cocktail exotique, 2 centilitres de glace et 15 grammesde fruits confits ; celle d’une coupe tropicale 5 centilitres decocktail exotique, 2 centilitres de glace et 25 grammes de fruitsconfits.Chaque jour, l’atelier de pâtisserie peut préparer au maximum1 600 centilitres de cocktail exotique, 520 centilitres de glaceet 5000 grammes de fruits confits.Soit x le nombre de coupes créoles et y le nombre de coupes tropicalesservies chaque jour.1. Écrire les contraintes de confection des coupes.À tout couple (x ; y) on associe le point M(x ; y) dans un repère(O ; i , j ) où 1 centimètre représente 20 coupes sur chaque axe.2. Déterminer graphiquement l’ensemble des points M, pour lesquelsles contraintes de la question précédente sont vérifiées.3. Sachant qu’une coupe créole est vendue 2 euros et une coupetropicale 1,50 euro :a. calculer, en fonction de x et y, la recette journalière R ;b. calculer les coordonnées du point I, intersection de la droited’équation 8x +5y = 1 600 et de la droite d’équation3x +5y = 1000 ;c. déterminer le couple (x ; y) pour lequel R est maximale etcalculer cette valeur maximale.77 Les bœufs de NewtonTrois bœufs ont mangé en deux semaines l’herbe contenue dansdeux arpents de prés, plus l’herbe qui y a poussé pendant cesdeux semaines.Deux bœufs ont mangé en quatre semaines l’herbe contenuedans deux arpents, plus l’herbe qui y a poussé pendant cesquatre semaines.Combien faudrait-il de bœufs pour manger en six semaines,l’herbe contenue dans six arpents, plus l’herbe qui y pousseraitpendant six semaines ?On suppose que l’herbe croît uniformément et que les bœufsmangent également.Indication : Soit x la quantité d’herbe contenue dans un arpent, y laquantité d’herbe mangée par un bœuf en une semaine, z la quantitéd’herbe poussée sur un arpent pendant une semaine et b le nombre debœufs cherché…78 Le prix des soucisAu pays des merveilles, seules les voyelles ont un prix, les consonnessont gratuites.C’est ainsi qu’une pivoine coûte seize flodors, une rose en coûtehuit, un œillet quinze, un géranium coûte autant qu’un œillet etun dahlia autant qu’une rose.Mais quel est donc, en flodors, le prix d’un souci ?60r chapitre 2 Systèmes