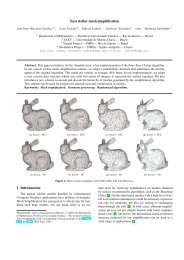
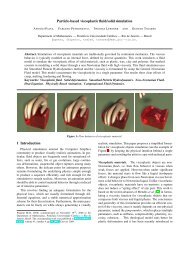
Aula 8 - PUC-Rio

Resumo
Aula 8: Integral de linha e trabalho
Nesta aula vamos utilizar os comandos do Maple para calcular integrais de linha
sobre curvas parametrizadas planas e espaciais. Vamos também calcular trabalhos
sobre campos vetoriais 2D e 3D.
Cola
O with(VectorCalculus):
with(linalg):
with(plots):
Considere a seguinte curva parametrizada: semi-círculo (t=0..Pi)
O Cx:=t->cos(t);
Cy:=t->sin(t);
plot([Cx(t),Cy(t), t=0..Pi],scaling=constrained);
Cx := ?
Cy := ?
Integral de Linha 2D
K1.0 K0.5 0 0.5 1.0
Com f = x ou y, podemos calcular a posição do baricentro
O fx := (x,y) -> x ;
fy := (x,y) -> y ;
1.0
0.6
0.2
Integral de linha envolve substituiçao de x e y pelas equações da curva, e o
jacobiano sendo a norma do vetor velocidade da curva. Desta forma, podemos
definir o método abaixo para obter a integral de linha sobre uma curva
parametrizada C( C(x), C(y) ).
O IntegralLinha := proc( a,b, Cx,Cy, f )
return int( f( Cx(t), Cy(t) ) * sqrt( diff(Cx(t),t)^2 +
diff(Cy(t),t)^2 ), t=a..b);
end proc ;
O Cx:=t->cos(t);
Cy:=t->sin(t);
f := (x,y) -> 1 ;
comp := IntegralLinha( 0,Pi, Cx,Cy, f ) ;
comp := π

IntegralLinha( 0,Pi, Cx,Cy, fx )/comp ;
IntegralLinha( 0,Pi, Cx,Cy, fy )/comp ;
0
2
π
Exercício: determinar o comprimento de uma senoide entre 0 e Pi.
Trabalho
Considere o campo vetorial F abaixo.
O F := (x,y) -> [ y*(1+y^2)/(1+x^2+y^2)^(3/2) ,
x*(1+x^2)/(1+x^2+y^2)^(3/2) ] :
fieldplot(F(x,y),x=-2..2, y=-2..2);
2
1
K2 K1 0 1 2
K1
K2
Então podemos determinar o trabalho realizado pelo campo vetorial F sobre uma
curva C, pelo método definido abaixo (o local do proc é para dizer ao Maple de não
procurar um dC definido anteriormente)
O Trabalho := proc( a,b, Cx,Cy, F )
local dC ;
dC := [ D(Cx), D(Cy) ] :
return int( dotprod( F( Cx(t), Cy(t) ), dC(t) ), t=a..b ) ;
end proc ;
Trabalho de F num oitavo de círculo
O Cx := t -> cos(t) ;
Cy := t -> sin(t) ;
Trabalho( 0,Pi/4, Cx, Cy, F ) ;
1
2
4
Exercício: determinar o trabalho da gravidade F=(0,-10) sobre uma senoide entre 0
e Pi/2.

Integral de Linha 3D
Exatamente como acima, a integral de linha envolve substituiçao de x , y e z pelas
equações da curva, e o jacobiano sendo a norma do vetor velocidade da curva.
O IntegralLinha3D := proc( a,b, Cx,Cy,Cz, f )
return int( f( Cx(t), Cy(t), Cz(t) ) * sqrt( diff(Cx(t),t)
^2 + diff(Cy(t),t)^2 + diff(Cz(t),t)^2 ), t=a..b);
end proc ;
O Cx := t -> cos(t) ;
Cy := t -> sin(t) ;
Cz := t -> t ;
IntegralLinha3D( 0, 2*Pi, Cx,Cy,Cz, 1 ) ;
2 2 π
Exercício: determinar as 3 coordenadas do baricentro deste arco de helice..
Trabalho 3D
Considere o campo vetorial dado por
O F := (x,y,z) -> [y+z, z+x, x+y] :
fieldplot3d(F(x,y,z),x=-2..2, y=-2..2, z=-2..2, axes=frame);
-2.2
-0.2
y
1.8
1.8
-2.2
-0.2
z
-2.2
1.8
-0.2
x
Podemos determinar o trabalho realizado por um campo vetorial F ao longo de
uma curva C(C(x), C(y), C(z)) pelo método seguinte:
O Trabalho3d := proc( a,b, Cx,Cy,Cz, F )
local dC ;
dC := [ D(Cx), D(Cy), D(Cz) ] :

O
return int( dotprod( F( Cx(t), Cy(t), Cz(t) ), dC(t) ), t=
a..b ) ;
end proc :
Trabalho3d( 0, 2*Pi, Cx,Cy,Cz, F ) ;
2 π
Exercício: calcular o trabalho da forca eletrica gerada por uma particula na origem
ao longo do arco de helice de 0 a 2*Pi.