6. predavanje
6. predavanje
6. predavanje
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
RAD, SNAGA, ENERGIJA<br />
Mehanički rad<br />
Fizički smisao rada se u mnogome razlikuje od našeg svakodnevnog poimanja rada. Zato<br />
odmah recimo da je rad skalarni proizvod sile pod čijim dejstvom telo učini neki pomeraj i tog<br />
pomeraja:<br />
r r<br />
r r<br />
A = F ⋅∆<br />
= F ⋅ ∆r<br />
⋅cos<br />
∠ F,<br />
∆<br />
( ( )<br />
2<br />
kgm<br />
Jedinica za rad je Džul (J): [ A ] = J = Nm =<br />
2<br />
s<br />
Iz gornjeg izraza vidimo da rad zavisi od vrednosti kosinusa ugla kojeg zaklapa vektor sile sa<br />
vektorom pomeraja. Pošto znamo da f-ja cos može da ima vrednosti od -1 do 1 (uključujući nulu),<br />
postavlja se pitanje da li to znači da rad neke sile može biti negativan ili nula pri pomeranju nekog<br />
tela? Odgovor je potvrdan, što se može videti i na sledećim primerima.<br />
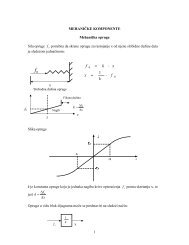
N<br />
Na slici je prikazano telo koje leži na<br />
horizontalnoj podlozi. Na njega<br />
deluje konstantna horizontalna sila<br />
F<br />
F r pod čijim dejstvom će se telo<br />
F pomeriti za ∆ r T<br />
. Osim ove sile na<br />
telo deluje sila teže, normalna sila<br />
mg<br />
(dejstvo podloge) i sila trenja.<br />
∆r<br />
Napišimo čemu je jednak rad svake<br />
od ovih sila.<br />
A F<br />
= F ⋅ ∆r<br />
cos 0 = F ⋅ ∆r〉<br />
0 rad sile F r je pozitivan.<br />
π<br />
A mg<br />
= mg∆r<br />
cos = mg∆r<br />
⋅0<br />
= 0<br />
2<br />
sila teže ne vrši rad pri pomeranju tela za ∆ r .<br />
π<br />
A N<br />
= N∆r<br />
cos = 0 normalna sila podloge ne vrši rad.<br />
2<br />
AF T<br />
= FT<br />
∆r<br />
cos π 〈0 rad sile trenja je negativan (sila trenja pruža otpor kretanju i protiv nje se<br />
mora izvršiti rad da bi se telo pomerilo za ∆ r .<br />
Dakle, uopšteno govoreći mogući su sledeći slučajevi:<br />
A > 0 ,<br />
π<br />
0 ≤ θ <<br />
2<br />
A = 0 ,<br />
π<br />
θ =<br />
2<br />
A < 0 ,<br />
π<br />
θ ><br />
2<br />
gde je θ ugao koji zaklapaju vektori sile i pomeraja.<br />
Razmotrimo sledeći primer sa slike dole levo. Neka na telo koje se nalazi na horizontalnoj<br />
podlozi deluje sila F r pod uglom θ u odnosu na pravac x ose (pravac pomeraja). Silu F r možemo<br />
razložiti na dve komponente F r i F<br />
r . U skladu sa gore izloženim razmatranjem, zaključujemo da<br />
x<br />
y<br />
rad vrši samo komponenta sile koja je u pravcu pomeraja (horizontalna komponenta), dok je rad<br />
vertikalne komponente sile jednak nuli.
y<br />
Postavlja se pitanje šta ako je<br />
intenzitet ili pravac sile promenljiv<br />
N<br />
F duž pomeraja? Pre nego što damo<br />
y<br />
θ<br />
odgovor na ovo pitanje uočimo (uz<br />
F<br />
pomoć slike) da promena pravca sile,<br />
θ F x<br />
odnosno ugla θ, istovremeno znači i<br />
x promenu intenziteta horizontalne<br />
F T<br />
komponente koja je odgovorna za<br />
vršenje rada duž horizontalnog<br />
mg<br />
∆r<br />
pomeraja. Dakle, ako je sila<br />
promenljivog intenziteta moramo<br />
uzeti u obzir elementarni rad koji sila vrši na elementarnom putu.<br />
Neka je na slici desno prikazan grafik promene horizontalne komponente sile duž pomeraja po x osi.<br />
Potrebno je ukupan pomeraj izdeliti na deliće<br />
dx 1, dx2,...<br />
dx i<br />
,... dx n<br />
, takve da je sila na tom<br />
pravolinijskom deliću puta konstantnog intenziteta. Rad<br />
F x<br />
2<br />
sile na tom elementarnom putu je:<br />
r r<br />
r r<br />
dA = Fdr = Fdr cos( < ( F,<br />
dr<br />
) = Fxdx<br />
1<br />
dA i<br />
Što geometrijsko odgovara površini osenčenog<br />
pravougaonika. Da bismo dobili ukupan rad sile na putu<br />
dx i<br />
od x 1 do x 2 , potrebno je sumirati površine svih<br />
pravougaonika, tj. izračunati površinu ispod krive na<br />
slici od tačke 1 do tačke 2. Tako dobijamo da je:<br />
x<br />
A<br />
x2<br />
= F x<br />
dx ,<br />
x 1 x 2<br />
12<br />
∫<br />
x1<br />
Odnosno, u opštem slučaju, ukupan rad sile pri premeštanju tela od tačke 1 do tačke 2 je:<br />
2<br />
r r<br />
A12 = ∫ F ⋅ d<br />
Ukoliko na telo istovremeno deluje više sila, onda je:<br />
2<br />
r<br />
2 n<br />
r r r<br />
A = F ⋅dr<br />
= F ⋅ dr =<br />
12<br />
∫<br />
1<br />
rez<br />
∫∑<br />
1 i=<br />
1<br />
1<br />
i<br />
n<br />
2<br />
∑∫<br />
r r<br />
F dr =<br />
n<br />
∑<br />
i<br />
i= 1 1 i=<br />
1<br />
što znači da ukupan rad možemo dobiti sabiranjem radova koje je izvršila svaka sila pojedinačno, a<br />
to predstavlja princip superpozicije radova.<br />
Snaga<br />
Snaga je veličina koja karakteriše brzinu vršenja rada i (pri translatornom kretanju) može se naći iz:<br />
r r<br />
dA F ⋅ dr r r<br />
P = = = F ⋅v<br />
dt dt<br />
Dakle, to je skalarna veličina koja zavisi od intenziteta sile i brzine i ugla kojeg zaklapaju vektori<br />
sile i brzine. Jedinica za snagu je Vat (W):<br />
2<br />
J kgm<br />
[ P ] = W = =<br />
3<br />
s s<br />
A<br />
i
Energija<br />
Neka se dve bilijarske kugle kreću po istom pravcu u suprotnom smeru, dakle jedna prema<br />
drugoj. Ako se razlikuju po masi ili ako su im intenziteti brzina različiti, tada je ukupan impuls<br />
sistema (zbir impulsa svake kugle pojedinačno) različit od nule. Neka, zatim, kugle dožive<br />
apsolutno neelastičan sudar, tako da nakon sudara miruju. Ukupan impuls sistema u tom slučaju je<br />
jednak nuli. Dakle, ako bismo posmatrali samo impuls i pomoću njega opisivali kompletnu<br />
dinamiku sistema, morali bismo da zaključimo da je kretanje koje je postojalo pre sudara „iščezlo“.<br />
Eksperiment, međutim, pokazuje da je zbog sudara došlo do porasta temperature kugli što, kako<br />
ćemo kasnije videti, predstavlja manifestaciju unutrašnjeg kretanja. Ipak, porediti impuls kugli pre<br />
sudara i temperaturu posle nije moguće, ako ni zbog čega drugog ono zbog toga što je impuls<br />
vektorska, a temperatura skalarna veličina. Zato uvodimo novu skalarnu veličinu koja će, pored<br />
impulsa, karakterisati dinamiku tela (sistema) i njegovu sposobnost da vrši rad, a to je energija.<br />
Postoji više tipova energije (unutrašnja, toplotna, hemijska,...) ali ćemo se mi, u ovom odeljku,<br />
baviti samo jednim tipom i to mehaničkom energijom, koja predstavlja zbir kinetičke i potencijalne<br />
energije tela.<br />
Kintička energija<br />
Kinetička energija predstavlja sposobnost tela da vrši rad zahvaljujući svom kretanju.<br />
Neka na telo deluje više sila istovremeno. Tada je elementarni rad koji vrše te sile na<br />
elementarnom pomeranju tela jednak:<br />
r r<br />
dA = Frez<br />
⋅ dr<br />
Primenjujući na ovaj iraz II Njutnov zakon i činjenicu da je u oblasti klasične mehanike (gde su<br />
brzine tela mnogo manje od brzine svetlosti) masa tela konstantna veličina, dobijamo:<br />
r r r<br />
r dp ⋅dr<br />
r r r r r r 1 2 ⎛ 1 2 ⎞<br />
dA = Frez<br />
⋅ dr = = v ⋅ dp = v ⋅ d( mv ) = mv ⋅dv<br />
= mvdv = md( v ) = d⎜<br />
mv ⎟ = dEk<br />
(*)<br />
dt<br />
2 ⎝ 2 ⎠<br />
gde smo sa E k označili kinetičku energiju tela pri translatornom kretanju. Dakle:<br />
1 2 Ek = mv<br />
2<br />
Takođe vidimo da kinetičku energiju možemo povezati sa impulsom na način:<br />
( mv)<br />
2<br />
E 1 p<br />
= =<br />
k<br />
2 m 2 m<br />
Iz izraza (*) dobijamo da je ukupan rad rezultante spoljašnjih sila jednak promeni kinetičke<br />
energije sistema, jer je:<br />
2 2<br />
1 2 1 2<br />
A = ∫dA<br />
= ∫ dEk<br />
= Ek<br />
2<br />
− Ek1<br />
= mv2<br />
− mv1<br />
2 2<br />
1 1<br />
što znači da bismo promenili kinetičku energiju tela moramo vršiti rad ili telo vrši rad na račun<br />
promene svoje kinetičke energije.<br />
Ako je rezultanta spoljašnjih sila jednaka nuli (takve sisteme nazivamo izolovanim sistemima),<br />
onda:<br />
r r<br />
dA = Frez ⋅ dr = dEk<br />
= 0 ⇒ Ek<br />
= const<br />
ili rečima: u izolovanom sistemu ukupna kinetička energija je konstantna.<br />
2<br />
kgm<br />
Jedinica za energiju u SI sistemu je ista kao i za rad i to je Džul:[ E ] = J =<br />
2<br />
s<br />
2
Konzervativne sile<br />
Sve sile koje su centralne (deluju duž pravca koji spaja centre dva tela) i stacionarne (ne<br />
zavise od brzine, ne menjaju se u toku vremena) nazivaju se konzervativne sile. One koje ne<br />
ispunjavaju ove uslove nazivaju se disipativne sile. Iz dosadašnjeg razmatranja možemo zaključiti<br />
da su, npr., gravitaciona i elastična sila konzervativne (kao i elektrostatička, npr.), a da su sile trenja<br />
i otpora, disipativne sile. Fizičko polje u kome vladaju konzervativne sile naziva se potencijalno<br />
polje (dakle, gravitaciono polje je potencijalno polje).<br />
Karakteristika konzervativnih sila je da rad ovih sila ne zavisi od a<br />
oblika putanje tela, već samo od početnog i krajnjeg položaja tela. Tako,<br />
2<br />
b<br />
prema slici desno, možemo napisati da je:<br />
1 c<br />
A<br />
1a2<br />
= A1<br />
b2<br />
= A 1c2<br />
.<br />
Takođe, u slučaju konzervativnih sila važi da je rad koji sila izvrši pomerajući<br />
telo po zatvorenoj krivolinijskoj putanji, jednak 0, tj.: A 0<br />
121 =<br />
Rad konzervativnih sila jednak je negativnoj promeni potencijalne energije tela:<br />
k<br />
A = −∆E<br />
Potencijalna energija<br />
Potencijalna energija predstavlja sposobnost tela da vrši rad zahvaljujući svom položaju. Za<br />
razliku od kinetičke energije, čiji smo izraz dosledno izveli polazeći od definicije kinetičke energije,<br />
slučaj potencijalne energije je nešto složeniji. Izraz za potencijalnu energiju moramo izvesti za<br />
svaki slučaj pojedinačno, jer on zavisi od:<br />
‣ tipa sile (ili polja) i<br />
‣ izbora referentnog nivoa na kome je potencijalna energija jednaka nuli.<br />
Da bismo lakše razumeli o čemu je reč, izvedimo izraz za potencijalnu energiju u slučaju (različiti<br />
tipovi sile):<br />
1. gravitacione i<br />
2. elastične sile,<br />
a u slučaju gravitacione sile uzmimo da je nivo na kome je potencijalna energija jednaka nuli<br />
smešten:<br />
a) u beskonačnosti,<br />
b) na površini Zemlje.<br />
1. Gravitaciona potencijalna energija<br />
a) E ( ∞) = 0<br />
p<br />
p<br />
Na slici desno prikazano je telo mase m 1 koje deluje<br />
gravitacionom silom F r<br />
g<br />
na telo mase m 2 , pri čemu je:<br />
r m1m<br />
2<br />
r<br />
F g<br />
− γ<br />
2 0<br />
r<br />
Rad gravitacione sile na pomeranju tela za d r je:<br />
r r m1m<br />
2<br />
r r<br />
dA = Fg<br />
⋅dr<br />
= −γ<br />
0<br />
⋅ dr<br />
2<br />
r<br />
m 1 m 2<br />
r 0 F g<br />
r
Imajući u vidu da je r 0<br />
ort (jedinični vektor) :<br />
r r<br />
r r<br />
0<br />
⋅ dr = r0<br />
dr cos( ∠( 0<br />
,dr )) = r0<br />
dr cos0<br />
= 1⋅<br />
dr ⋅1,<br />
dobijamo:<br />
m1m<br />
2<br />
dA = −γ r0<br />
dr<br />
2<br />
r<br />
Kako smo u ovom tekstu već naglasili, gravitaciona sila je konzervativna sila, a rad konzervativnih<br />
sila je jednak negativnoj promeni potencijalne energije. Zato:<br />
m m<br />
dA = −γ<br />
Ep<br />
r<br />
1 2<br />
m1m<br />
2<br />
dr = −dE<br />
p<br />
⇒ dE<br />
p<br />
= γ dr ⇒ ∫dE<br />
p<br />
=<br />
2<br />
2<br />
r<br />
r<br />
∫γ<br />
0 ∞<br />
(Ovde smo određujući granice integrala iskoristili činjenicu da smo referentni nivo postavili u<br />
beskonačnost, tj E p =0 za r = ∞ ).<br />
Dalje je:<br />
r<br />
Ep<br />
⎛ 1 ⎞<br />
⎛ 1 1 ⎞<br />
E<br />
p<br />
= −γ<br />
m1m<br />
2⎜<br />
⎟ ⇒ E<br />
p<br />
− 0 = −γm1m<br />
2⎜<br />
− ⎟ ⇒ E<br />
⎝ r ⎠<br />
⎝ r ∞<br />
∞<br />
⎠<br />
i konačno, gravitaciona potencijalna energija je:<br />
m1m<br />
2<br />
E p<br />
= −γ<br />
r<br />
Grafički prikazana ova zavisnost data je na slici dole.<br />
m1m<br />
2<br />
r<br />
2<br />
dr<br />
⎛ 1 ⎞<br />
= −γm1m<br />
2⎜<br />
− 0⎟<br />
⎝ ⎠<br />
0<br />
p<br />
r<br />
E p<br />
F
E<br />
R + h<br />
R + h<br />
p<br />
z<br />
z<br />
Mm<br />
Ep ⎛ 1 ⎞<br />
⎛ 1 1 ⎞<br />
∫dE<br />
= ∫ ⇒ = − ⎜ ⎟ ⇒ − = −<br />
⎜ −<br />
⎟<br />
p<br />
γ dr E<br />
p<br />
γMm<br />
E<br />
p<br />
0 γMm<br />
⇒<br />
2<br />
r<br />
0<br />
⎝ r ⎠<br />
⎝ Rz<br />
+ h R<br />
0<br />
R<br />
R<br />
z<br />
z<br />
⎠<br />
z<br />
Mmh<br />
E<br />
p<br />
= γ<br />
2⎛ h ⎞<br />
R<br />
⎜ +<br />
⎟<br />
z<br />
1<br />
⎝ Rz<br />
⎠<br />
Za visine h koje su mnogo manje od poluprečnika Zemlje:<br />
h<br />
h