You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Bu fikirleri ilk ortaya atan ve yeni bir kaos kavramı oluşturan kişi Amerikalı Matematikçi ve Meteoroloji<br />
Uzmanı Edward Lorenz 'tir.<br />
Lorenz bu keşfini, 1960'ların başında hava durumu modelleri üzerinde çalışırken bir yanlışlık sonucu yapmıştır.<br />
Simülasyonu için erken dönen bilgisayarlardan bir LGP-30 kullanıyordu. Bir noktada simülasyonu tekrar çalıştırması<br />
gerekti. Bunun için bilgisayarın kullandığı sayıların çıktısını aldı ve geri geldiğinde bu şeyleri tekrar kağıttan<br />
bilgisayara girdi. Bilgisayar geride olarak aynı sayıları kullandığı için, ilk seferkiyle aynı sonuçlara varması gerekirdi.<br />
Fakat öyle olmadı. Bilgisayar hesaplamalarında bilgiden sonra altı basamak hesaplıyor fakat çıktıyı basarken üç<br />
basamak kadar yuvarlıyordu.<br />
Örneğin belleğindeki sayı 0,506127 ise çıktıda 0,506 yazıyordu. Lorenz de bu<br />
yuvarlatılmış sayıları girmişti. Bu iki değer arasındaki ufacık bir farkın (0,000127)<br />
simülasyonun sonunda ufacık bir farka yol açtığını tahmin ediyordu. Fakat öyle<br />
olmadı. Çok büyük bir sürprizle karşılaştı. Lorenz ufacık değişimlerin çok büyük<br />
etkilere yol açabileceğini keşfetmişti. Bu simülasyon bugün "doğrusal olmayan<br />
davranış" diye adlandırdığımız şeyin bir örneğiydi. Uzun vadeli hava tahmini<br />
yapmanın zorluğu burdadır: gerçek hava durumunu etkileyen değişkenleri asla<br />
sonsuz kesinlikte bilemeyiz. Bilardo masası örneğiyle aynı durum,sadece çok daha<br />
karmaşığı. Günümüzde birkaç gün içinde yağmur yağıp yağmayacağını makul bir<br />
güvenilirlikte söyleyebiliyoruz fakat önümüzdeki yılın aynı günü yağıp<br />
yağmayacağını asla bilemeyiz.<br />
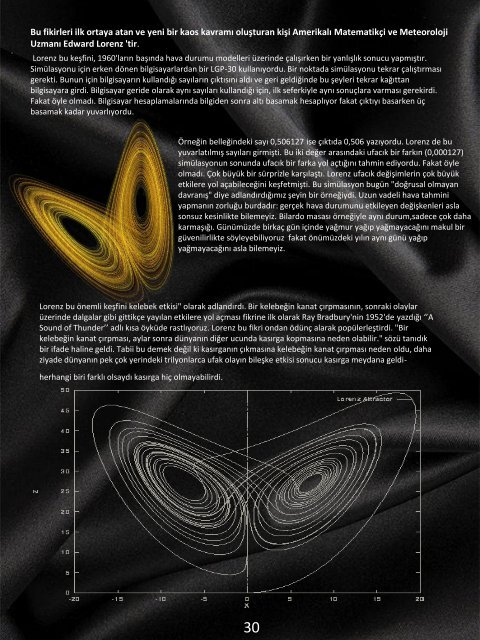
Lorenz bu önemli keşfini kelebek etkisi" olarak adlandırdı. Bir kelebeğin kanat çırpmasının, sonraki olaylar<br />
üzerinde dalgalar gibi gittikçe yayılan etkilere yol açması fikrine ilk olarak Ray Bradbury'nin 1952'de yazdığı ‘’A<br />
Sound of Thunder’’ adlı kısa öyküde rastlıyoruz. Lorenz bu fikri ondan ödünç alarak popülerleştirdi. "Bir<br />
kelebeğin kanat çırpması, aylar sonra dünyanın diğer ucunda kasırga kopmasına neden olabilir." sözü tanıdık<br />
bir ifade haline geldi. Tabii bu demek değil ki kasırganın çıkmasına kelebeğin kanat çırpması neden oldu, daha<br />
ziyade dünyanın pek çok yerindeki trilyonlarca ufak olayın bileşke etkisi sonucu kasırga meydana geldiherhangi<br />
biri farklı olsaydı kasırga hiç olmayabilirdi.<br />
30