Equations différentielles d'ordre 2

Équations différentielles d’ordre 2 Lycée Louis Armand, Poitiers
Exercice 8 : Amortissement
L’étude d’un phénomène d’amortissement conduit à la résolution de l’équation différentielle
(E) y + 2y + 2y = 0
où y est une fonction de la variable x, définie et deux fois dérivable sur ¢ .
1. Résolution de l’équation différentielle (E)
a) Résoudre (E).
b) Déterminer la solution particulière g de (E) satisfaisant aux conditions initiales :
2. Étude d’une solution de (E) sur [0 π]
Soit f la fonction définie sur [0 π] par
a) Établir que : cos x sin ¥ π
x = 2 x¡ sin .
4
En déduire le signe de (cos x sin x) sur [0 π].
g(0) = 0 et g (0) = 1¢
f (x) = e¨ x sin x¢
b) Calculer la dérivée f de f . En déduire les variations de f sur [0 π].
c) Construire C f , la courbe représentative de la fonction f dans un repère orthogonal (unités : 5 cm en abscisse,
10 cm en ordonnée).
Exercice 9 : Une suspension de voiture
– Partie A –
La suspension d’une voiture est schématisée par un ressort vertical de force de rappel k = 1 36¢ 10 4 Nm¨ 1 .
La masse m de la voiture est de 800 kg.
On démontre en mécanique que l’équation du mouvement vertical de cette voiture est de la forme :
y + b k
y + y = 0
m m
où y désigne l’amplitude de l’oscillation en fonction du temps t, b étant une constante qui peut être choisie égale
à 1 600.
1. Résoudre cette équation différentielle.
2. Déterminer la solution particulière telle qu’à l’instant t = 0, les conditions suivantes soient vérifiées :
y(0) = 1 £
y (0) 1¢ =
– Partie B –
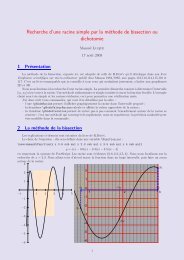
On considère la fonction numérique f de la variable réelle t, définie sur [0 π] par : f (t) = e¨ t cos 4t .
La courbe Γ de f est donnée sur la figure ci-dessous
1
0.5
0
-0.5
-1
0 0.5 1 1.5 2 2.5 3
4