Volledige inhoud (pdf) - Pythagoras
Volledige inhoud (pdf) - Pythagoras
Volledige inhoud (pdf) - Pythagoras
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
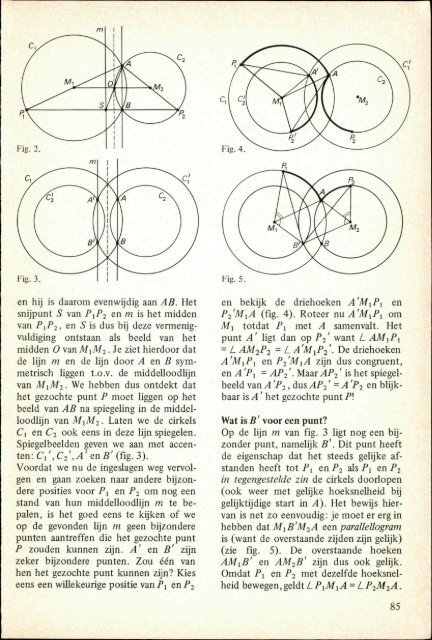
Fig. 3. I<br />
en hij is daarom evenwijdig aan AB. Het<br />
snijpunt S van P1P2 en m is het midden<br />
van P1P2, en S is dus bij deze vermenigvuldiging<br />
ontstaan als beeld van het<br />
midden O van M1M2. Je ziet hierdoor dat<br />
de lijn m en de lijn door A en B symmetrisch<br />
liggen t.o.v. de middelloodlijn<br />
van M1M2. We hebben dus ontdekt dat<br />
het gezochte punt P moet liggen op het<br />
beeld van AB na spiegeling in de middelloodlijn<br />
van M1M2. Laten we de cirkels<br />
Ci en C2 ook eens in deze lijn spiegelen.<br />
Spiegelbeelden geven we aan met accenten:<br />
C,'^2', ,4'en fi'(fig. 3).<br />
Voordat we nu de ingeslagen weg vervolgen<br />
en gaan zoeken naar andere bijzondere<br />
posities voor Pi en P2 om nog een<br />
stand van hun middelloodlijn m te bepalen,<br />
is het goed eens te kijken of we<br />
op de gevonden lijn m geen bijzondere<br />
punten aantreffen die het gezochte punt<br />
P zouden kunnen zijn. A' en B' zijn<br />
zeker bijzondere punten. Zou één van<br />
hen het gezochte punt kunnen zijn? Kies<br />
eens een willekeurige positie van Pi en P2<br />
en bekijk de driehoeken A'MiPi en<br />
P2'MiA (fig. 4). Roteer nuA'M^j om<br />
Afi totdat Pi met A samenvalt. Het<br />
punt A' ligt dan op P2' want L AM1P1<br />
= L AM2P2 = LA'MyPi'. De driehoeken<br />
A'MiPi en P^MiA zijn dus congruent,<br />
en A 'Pi = AP2' ■ Maar AP 2' is het spiegelbeeld<br />
vanA'P2, dus AP2' =A'P2 en blijkbaar<br />
is A' het gezochte punt P!<br />
Wat is B' voor een punt?<br />
Op de lijn m van fig. 3 ligt nog een bijzonder<br />
punt, namelijk B'. Dit punt heeft<br />
de eigenschap dat het steeds gelijke afstanden<br />
heeft tot P, en P2 als P] en P2<br />
in tegengestelde zin de cirkels doorlopen<br />
(ook weer met gelijke hoeksnelheid bij<br />
gelijktijdige start in A). Het bewijs hiervan<br />
is net zo eenvoudig: je moet er erg in<br />
hebben dat MiB'M2A een parallellogram<br />
is (want de overstaande zijden zijn gelijk)<br />
(zie fig. 5). De overstaande hoeken<br />
AMiB' en AM2B' zijn dus ook gelijk.<br />
Omdat P! en P2 met dezelfde hoeksnelheid<br />
bewegen,geldt ZP^!^ = Z^Afj^.<br />
85