Selectividad 2010-11 modelo 4 Opción A - Quidiello
Selectividad 2010-11 modelo 4 Opción A - Quidiello
Selectividad 2010-11 modelo 4 Opción A - Quidiello
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
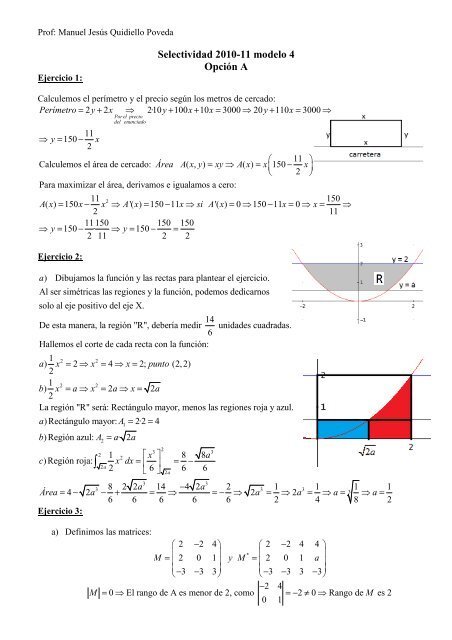
Prof: Manuel Jesús <strong>Quidiello</strong> Poveda<br />
Ejercicio 1:<br />
<strong>Selectividad</strong> <strong>2010</strong>-<strong>11</strong> <strong>modelo</strong> 4<br />
<strong>Opción</strong> A<br />
Calculemos el perímetro y el precio según los metros de cercado:<br />
Perímetro = 2y + 2x ⇒ 2·10 y + 100x + 10x = 3000 ⇒ 20y + <strong>11</strong>0x = 3000 ⇒<br />
Por el precio<br />
del enunciado<br />
<strong>11</strong><br />
⇒ y = 150 − x<br />
2<br />
⎛ <strong>11</strong> ⎞<br />
Calculemos el área de cercado: Área A( x, y) = xy ⇒ A( x) = x⎜150 − x⎟<br />
⎝ 2 ⎠<br />
Para maximizar el área, derivamos e igualamos a cero:<br />
<strong>11</strong> 2<br />
150<br />
A( x) = 150x − x ⇒ A'( x) = 150 −<strong>11</strong>x ⇒ si A'( x) = 0 ⇒150 − <strong>11</strong>x = 0 ⇒ x = ⇒<br />
2 <strong>11</strong><br />
<strong>11</strong> 150 150 150<br />
⇒ y = 150 − · ⇒ y = 150 − =<br />
2 <strong>11</strong> 2 2<br />
Ejercicio 2:<br />
a)<br />
Dibujamos la función y las rectas para plantear el ejercicio.<br />
Al ser simétricas las regiones y la función, podemos dedicarnos<br />
solo al eje positivo del eje X.<br />
14<br />
De esta manera, la región "R", debería medir<br />
unidades cuadradas.<br />
6<br />
Hallemos el corte de cada recta con la función:<br />
1 2 2<br />
a) x = 2 ⇒ x = 4 ⇒ x = 2; punto (2,2)<br />
2<br />
1 2 2<br />
b) x = a ⇒ x = 2a ⇒ x = 2a<br />
2<br />
La región "R" será: Rectángulo mayor, menos las regiones roja y azul.<br />
a)<br />
Rectángulo<br />
mayor: A = 2·2 = 4<br />
b) Región azul: A = a· 2a<br />
2<br />
2<br />
c)Región roja: ∫ x dx<br />
2a<br />
2<br />
1<br />
3<br />
2<br />
3<br />
1 ⎡ x ⎤ 8 8a<br />
= ⎢ ⎥ = −<br />
2 ⎣ 6 ⎦ 6 6<br />
2a<br />
Área = 4 −<br />
Ejercicio 3:<br />
3 3<br />
3 8 2 2a 14 −4<br />
2a 2<br />
2a − + = ⇒ = − ⇒<br />
6 6 6 6 6<br />
3 1 3 1 1 1<br />
2a = ⇒ 2a<br />
= ⇒ a = 3 ⇒ a =<br />
2 4 8 2<br />
a) Definimos las matrices:<br />
⎛ 2<br />
⎜<br />
M =<br />
⎜<br />
2<br />
⎜<br />
⎝ −3 −2 0<br />
−3 4⎞ ⎟<br />
1<br />
⎟<br />
3⎟ ⎠<br />
⎛ 2<br />
* ⎜<br />
y M =<br />
⎜<br />
2<br />
⎜<br />
⎝ −3 −2<br />
0<br />
−3 4<br />
1<br />
3<br />
4 ⎞<br />
⎟<br />
a<br />
⎟<br />
−3⎟<br />
⎠<br />
M<br />
−2<br />
= 0 ⇒ El rango de A es menor de 2, como<br />
0<br />
4<br />
= −2 ≠ 0 ⇒<br />
Rango de M es 2<br />
1
Prof: Manuel Jesús <strong>Quidiello</strong> Poveda<br />
⎛ 2 −2 4 4 ⎞ ⎛ 2 −2 4 4 ⎞ ⎛ 2 −2<br />
4 4 ⎞<br />
⎜ ⎟ ⎜ ⎟ ⎜ ⎟<br />
⎜ ⎟ ⎜ ⎟ ⎜ ⎟<br />
⎜ −3 −3 3 −3⎟ ⎜ 0 −12 18 6 ⎟ ⎜ 0 0 0 6a −18⎟<br />
⎝ ⎠ ⎝ ⎠ ⎝ ⎠<br />
*<br />
Triangulo M ⇒ Rg 2 0 1 a = Rg 0 2 −3 a − 4 = Rg 0 2 −3 a − 4<br />
F2 − F1 2F3 + 3F1<br />
F3 + 6F2<br />
Si a a Rg M Rg M<br />
*<br />
6 − 18 = 0 ⇒ = 3 ⇒ ( ) = 2 = ( ) Sistema compatible indeterminado<br />
Si a Rg M<br />
*<br />
≠ 3 ⇒ ( ) = 3 ≠ 2 = Rg( M ) Sistema incompatible<br />
b resolvemos<br />
*<br />
) Tomando el caso a = 3 y la última matriz de M , :<br />
⎛ 2 −2<br />
4 4 ⎞<br />
⎜ ⎟<br />
1 3<br />
⎜<br />
0 2 −3 −1 ⎟<br />
⇒ 2y − 3z = −1⇒ y = − + z<br />
⎜ 2 2<br />
0 0 0 0 ⎟<br />
⎝ ⎠<br />
.<br />
⎛ 1 3 ⎞<br />
1<br />
⇒ 2x − 2y + 4z = 4 ⇒ 2x − 2⎜ − + z ⎟ + 4z = 4 ⇒ 2x + 2 − 3z + 4z = 4 ⇒ 2x = 2 − z ⇒ x = 1−<br />
z<br />
⎝ 2 2 ⎠<br />
2<br />
luego :<br />
1<br />
x = 1 − z<br />
2<br />
;<br />
1 3<br />
y = − + z<br />
2 2<br />
; z = z<br />
Ejercicio 4:<br />
a) Al contener el plano a la recta r, un punto de esta y su vector director pertenecen al plano<br />
pedido. Como pasa por el origen, el vector que una un punto de la recta y el origen también<br />
pertenece al plano, luego ya tenemos dos vectores y un punto para hallar la ecuación del<br />
plano:<br />
x − 1 y + 1 z − 3<br />
recta r ≡ = =<br />
3 2 −1<br />
El vector de la recta es: (3,2, − 1) punto de la recta: P = (1, −1,3)<br />
Vector entre el origen y P: OP = (1, −1,3)<br />
x y z<br />
El plano es : 3 2 − 1 = 0 ⇒ 5x −10 y − 5z = 0 ⇒ x − 2y − z = 0<br />
1 −1<br />
3<br />
→<br />
→ →<br />
b) Como contiene a la recta s, tanto un punto de s como su vector director pertenecen al plano.<br />
Como el plano es paralelo a la recta r, su vector director pertenece al plano:<br />
El vector de la recta r es: (3,2, − 1) punto de la recta: P = (1, −1,3)<br />
<br />
i j k<br />
<br />
→ <br />
Vector de s : 1 0 0 = j + 2k ⇒ v = 0,1, 2<br />
0 2 −1<br />
→<br />
x − 1 y + 1 z − 3<br />
( )<br />
El plano es : 3 2 − 1 = 0 ⇒ 5x − 6y + 3z − 20 = 0<br />
0 1 2<br />
s
Prof: Manuel Jesús <strong>Quidiello</strong> Poveda<br />
<strong>Opción</strong> B<br />
Ejercicio 1:<br />
2 ⎧− x + 70x si 18 < x < 50<br />
⎪<br />
Calculemos la función que genera los ingresos: f ( x) = ⎨ 400x<br />
⎪ si x ≥ 50<br />
⎩ x − 30<br />
⎧ − 2x + 70 si 18 < x < 50<br />
⎪<br />
Derivamos e igualamos la derivada a cero: f '( x)<br />
= ⎨ −12000<br />
si x ≥ 50<br />
⎪ 2<br />
⎩(<br />
x − 30)<br />
Si 18 < x < 50 ⇒ − 2x<br />
+ 70 = 0 ⇒ x = 35 vértice de la parábola<br />
−12000<br />
Si x ≥ 50 ⇒ = 0 Imposible y como la derivada es negativa, el máximo lo alcanzaria en x = 50<br />
( ) 2<br />
x − 30<br />
f (35) = 1225 > f (50) = 1000<br />
Por lo tanto, el máximo lo consigue a los 35 con unos ingresos<br />
de 1225 euros<br />
Ejercicio 2:<br />
a) Calcularé el punto de corte de cada recta con la función y comprobaré si la derivada de la<br />
función en ese punto coincide con la pendiente de la recta:<br />
Hallo f '( x) : f '( x) = − 4x + 3<br />
4 ± 0<br />
4<br />
f '(1) = −1<br />
que coincide con la pendiente de la recta, luego es tangente a esta<br />
2 2<br />
1)Corto la primera recta: − x + 1 = − 2x + 3x −1 ⇒ 2x − 4x + 2 = 0 ⇒ x = ⇒ x = 1<br />
2<br />
2)Corto la primera recta: 3 − 1 = − 2 + 3<br />
2<br />
x x x −1 ⇒ 2x = 0 ⇒ x = 0<br />
f '(0) = 3 que coincide con la pendiente de la recta, luego es tangente a esta<br />
Dibujamos la recta mediante una tabla de valores y la parábola:<br />
Recta 1º: Si x = 0 y = 1 ⇒ (0,1) Si x = 1 y = 0 ⇒ (1,0)<br />
Recta 2º: Si x = 0 y = −1 ⇒ (0, − 1) Si x = 1 y = 2 ⇒ (1, 2)<br />
3 1 ⎛ 3 1 ⎞<br />
Parábola : Vértice en Vx = Vy = ⇒ Vértice ⎜ , ⎟<br />
4 8 ⎝ 4 8 ⎠<br />
⎧ 1 ⎛ 1 ⎞<br />
,0<br />
2<br />
− 3 ± 1 ⎪x<br />
= punto ⎜ ⎟<br />
Corta al eje Y en (0, −1) Corta al eje X : − 2x + 3x − 1 = 0 ⇒ x = ⇒ ⎨ 2 ⎝ 2 ⎠<br />
−4<br />
⎪<br />
⎩ x = 1 punto<br />
( 1,0 )<br />
1<br />
Hallo el punto de corte entre las rectas: − x + 1 = 3x −1 ⇒ 4x = 2 ⇒ x =<br />
2<br />
Divido el área total en dos regiones (azul y roja) y las sumaré al final:<br />
1<br />
3 2 ⎡ ⎤<br />
1 1<br />
2 2 2 2 2x<br />
Área azul: ∫ ( 3x −1) − ( − 2x + 3x − 1) dx = 2x<br />
dx<br />
0 ∫ =<br />
0 ⎢<br />
3<br />
⎥<br />
⎣ ⎦<br />
3<br />
1 1<br />
2 2 ⎡2 x 2 ⎤ 2 7 1<br />
Área roja: ∫ ( − x + 1) −<br />
1 ( − 2x + 3x − 1) dx = ∫1<br />
( 2x − 4x + 2 ) dx = ⎢ − 2x + 2x<br />
= − =<br />
3<br />
⎥<br />
⎣ ⎦ 3 12 12<br />
2 2 1 2<br />
1 1 1<br />
El área total es + =<br />
12 12 6<br />
0<br />
=<br />
1<br />
12<br />
1
Prof: Manuel Jesús <strong>Quidiello</strong> Poveda<br />
Ejercicio 3:<br />
a) 1 2 ⎛ −<br />
A = ⎜<br />
⎝ 2<br />
1 ⎞⎛ −1 ⎟⎜<br />
−1⎠⎝ 2<br />
1 ⎞ ⎛ 3<br />
⎟ = ⎜<br />
−1⎠ ⎝ −4 −2⎞ ⎟<br />
3 ⎠<br />
⎛ −2 2A = ⎜<br />
⎝ 4<br />
2 ⎞<br />
⎟<br />
−2⎠ 3 2 ⎛<br />
A − 2A<br />
= ⎜<br />
⎝ −4 −2⎞ ⎛ −2<br />
⎟ + ⎜<br />
3 ⎠ ⎝ 4<br />
2 ⎞ ⎛1 ⎟ = ⎜<br />
−2⎠<br />
⎝0 0⎞<br />
⎟<br />
1⎠<br />
Hallamos la inversa de A:<br />
−1 | A | =<br />
2<br />
1<br />
= − 1<br />
−1 1 t ⎛<br />
A = ⎜<br />
⎝1 2 ⎞ adj 1 t ⎛ −<br />
⎟ ⇒ ( A ) = ⎜<br />
−1⎠ ⎝ −2 −1⎞<br />
1 −1<br />
⎛<br />
⎟ ⇒ A = ⎜<br />
−1⎠<br />
⎝ 2<br />
1⎞<br />
⎟<br />
1⎠<br />
Operamos :<br />
1<br />
A + 2I<br />
2<br />
1 2<br />
1 0<br />
0 1<br />
2 2<br />
1<br />
A<br />
1<br />
−<br />
⎛ −<br />
= ⎜<br />
⎝<br />
⎞ ⎛<br />
⎟ + ⎜<br />
− ⎠ ⎝<br />
⎞ ⎛<br />
⎟ = ⎜<br />
⎠ ⎝<br />
⎞<br />
⎟ =<br />
⎠<br />
b)<br />
Despejamos la matriz X:<br />
1<br />
( )<br />
A + XA + 5A = 4I ⇒ XA = 4I − 5A − A ⇒ X = 4I − 5A<br />
− A A<br />
2 2 2 −1<br />
Operamos :<br />
2 ⎛ 4 0⎞ ⎛ −5 5 ⎞ ⎛ 3 −2⎞ ⎛ 6 −3⎞ ⎛ 6 −3⎞⎛<br />
1 1⎞ ⎛ 0 3⎞<br />
4I − 5A<br />
− A = ⎜ ⎟ − ⎜ ⎟ − ⎜ ⎟ = ⎜ ⎟ ⇒ X = ⎜ ⎟⎜ ⎟ = ⎜ ⎟<br />
⎝ 0 4⎠ ⎝10 −5⎠ ⎝ −4 3 ⎠ ⎝ −6 6 ⎠ ⎝ −6<br />
6 ⎠⎝ 2 1⎠ ⎝ 6 0⎠<br />
Ejercicio 4:<br />
a) Hallamos la perpendicular común y para ello necesito los vectores de la recta, el vector<br />
perpendicular a ambas y en un punto de cada recta.<br />
<br />
v = (2, − 1,1) P = ( − 7,7,0) v = (0,0,1) P = (2, − 5,0)<br />
<br />
i<br />
<br />
v = 2<br />
<br />
j<br />
− 1<br />
<br />
k<br />
<br />
1 = −i − 2 j ⇒ v = ( −1, −2,0)<br />
r r s s t t<br />
0 0 1<br />
x + 7 y − 7 z<br />
<br />
Hallo el plano que forman v , P y v : 2 − 1 1 = 0 ⇒ 2x − y − 5z + 21 = 0<br />
r r t<br />
−1 −2<br />
0<br />
x − 2 y + 5 z<br />
<br />
Hallo el plano que forman v , P y v : 0 0 1 = 0 ⇒ 2x − y − 7 = 0<br />
s s t<br />
⎧2x<br />
− y − 5z + 21 = 0<br />
La recta t será: ⎨<br />
⎩ 2x − y − 7 = 0<br />
b) Aplico la fórmula de la distancia entre rectas:<br />
−1<br />
−2<br />
0<br />
0 0 1<br />
2 −1<br />
1<br />
−9<br />
12 0 15 15 5<br />
Pr Ps = ( −7,7,0) − (2, − 5,0) = ( −9,12,0) ⇒ d( r, s)<br />
= = = = 3 5<br />
( −1, −2,0)<br />
5 5