Diédricos intersecciones-a - IES San Blas

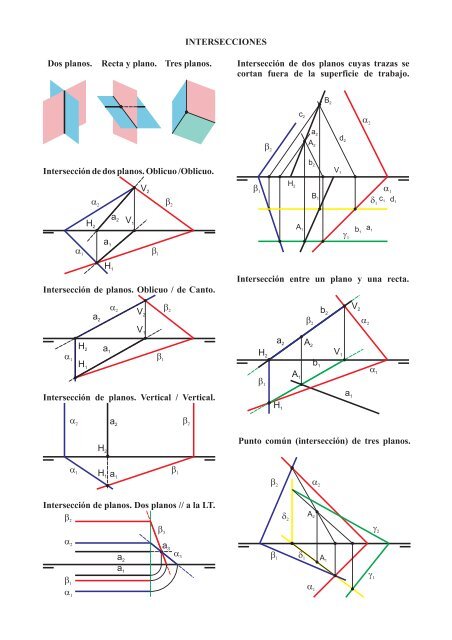
Dos planos.
Intersección de planos. Oblicuo / de Canto.
a
2
V
V
H2
a1
H
1
Intersección de planos. Vertical / Vertical.
a
2
H 2
a
H
1 1
Intersección de planos. Dos planos // a la LT.
a2
a1
a3
Recta y plano.
2
1
INTERSECCIONES
Tres planos.
Intersección de dos planos. Oblicuo /Oblicuo.
H 2
a1
H 1
a
2
V
1
V
2
Intersección de dos planos cuyas trazas se
cortan fuera de la superficie de trabajo.
H 2
c
A
1
2
A
b
a
2
2
2
B
1
B
2
V 1
d
2
b
1
a
c1
d1
Intersección entre un plano y una recta.
H
2
a
H
1
2
A
1
A
2
b
1
b
Punto común (intersección) de tres planos.
A
2
A
2
1
V
1
a
1
V
2
1

INTERSECCIONES
INTERSECCIÓN ENTRE DOS PLANOS
INTERSECCIÓN ENTRE RECTAYPLANO
ENTRE DOS PLANOS
ENTRE RECTAYPLANO
PUNTO COMÚN DE INTERSECCIÓN DE TRES PLANOS
Una recta es siempre el elemento común de intersección entre dos planos. Para su representación en
proyecciones, bastará con conocer dos de sus puntos.
El procedimiento para hallar la recta de intersección de dos planos consiste en prolongar sus trazas
verticales y horizontales hasta que se corten. Los dos puntos de corte son, respectivamente, los puntos
traza de la recta.
Si los planos son paralelos a la línea de tierra será necesaria la tercera proyección para saber si se cortan
o son paralelos.
En el caso de que las trazas, verticales u horizontales, de los planos sean paralelas entre sí, la recta de
intersección tendrá dicha proyección paralela a ellas.
Si las trazas del mismo nombre de los dos planos son paralelas entre sí y oblicuas a la línea de tierra, los
planos no tienen intersección.
Cuando dos trazas de los planos se salen fuera de los límites de la superficie de trabajo, es necesario el
uso de un plano auxiliar horizontal o frontal. Este plano dará dos rectas de intersección, con cada uno de
los anteriores, que tendrán un punto común. Este punto común pertenecerá a los tres planos y al unirlo
con el de corte de las otras trazas dará la recta de intersección.
Cuando las trazas horizontales y verticales se cortan fuera de los límites de la superficie de trabajo, se
necesitan dos planos auxiliares y seguir el procedimiento anterior para encontrar, en este caso, los dos
puntos de la recta de intersección.
Un punto es el elemento común de intersección entre recta y plano.
Para determinar las proyecciones del punto de intersección entre una recta y un plano es necesario
utilizar un plano auxiliar, vertical o de canto generalmente, que contenga a la recta. Seguidamente se
halla la recta de intersección de los dos planos y el punto de corte con la recta dada será el de
intersección con el plano.
En algunos casos será necesario utilizar un plano horizontal o frontal como auxiliar.
En las intersecciones de una recta con un plano proyectante no es necesario el plano auxiliar ya que el
punto de intersección debe coincidir con la traza del plano proyectante y se obtiene directamente.
PUNTO COMÚN DE INTERSECCIÓN DE TRES PLANOS
La intersección entre tres planos puede ser una recta, si están situados como las hojas de un libro, o un
punto, el resto de las situaciones.
Para hallar el punto común de tres planos se cogen dos de ellos determinando su recta de intersección.
El resto del problema se soluciona como en los de intersección entre recta y plano.

Intersección de planos. Oblicuo/Oblicuo.
V
V
2
1
a
a
2
1

Recta paralela a otra por un punto.
b
2
A a
2 2
b a
A
1 1
1
Plano paralelo a otro por un punto.
A a V
A
2 2 2
1
Plano paralelo a una recta por un punto.
V
2
A2
b2
V H
A1
H
a 1
1 2
1
b 1
V
1
a
a
2
1
PARALELISMO
R e c t a p a r a l e l a a o t r a d e P e r f i l .
a2 V3
V2
V2
b V b
2 3
3
a3 V H V H H
1 2 1 2 3
b H
H
1 1
1
Plano paralelo a otro (Paralelo a la LT).
V
V
2
1
Plano que contiene una recta paralelo a otra.
c b a
A
2 2 2
2
H 1
a
1
A
H
1
1
H V
2 1
a
H 3
1

PARALELISMO
Dos rectas son paralelas si pertenecen al mismo plano y no tienen puntos en común.
Por un punto sólo se puede trazar una recta paralela a otra.
Una recta es paralela a un plano si lo es a una recta de dicho plano.
Una recta es paralela a dos planos cuando lo es a la recta de intersección de ambos.
Dos planos son paralelos si no tienen puntos en común.
Por un punto sólo se puede trazar un plano paralelo a otro.
Las intersecciones de dos planos paralelos con un tercero son dos rectas paralelas.
CASOS DE PARALELISMO
PARALELISMO ENTRE DOS RECTAS
RECTAPARALELAAOTRAPOR UN PUNTO
PARALELISMO ENTRE DOS PLANOS
PLANO PARALELOAOTRO POR UN PUNTO
PARALELISMO ENTRE RECTAYPLANO
ENTRE DOS RECTAS
ENTRE DOS PLANOS
ENTRE RECTAYPLANO
Dos rectas paralelas en el espacio tienen, en diédrico, las proyecciones homónimas paralelas.
Para comprobar el paralelismo entre rectas de perfil se necesita su tercera proyección.
Para trazar una recta paralela a otra por un punto se trazan paralelas a las proyecciones
correspondientes por las del punto.
Dos planos paralelos en el espacio tienen las proyecciones homónimas paralelas.
Con algunas posiciones de planos paralelos será necesaria la tercera proyección para comprobar su
paralelismo.
Para trazar un plano paralelo a otro por un punto, es necesaria la utilización de una recta notable
(horizontal o frontal) que, a su vez, esté contenida en el plano y contenga al punto. Las
proyecciones (horizontales o verticales) correspondientes de la recta y del plano deben ser
paralelas.
Una recta es paralela a un plano si lo es a una recta de dicho plano.
PLANO PARALELOAUNARECTAPOR UN PUNTO
Cualquier plano que contenga una recta que pase por el punto y sea paralela a la recta dada será
paralelo a ella, habiendo infinitas soluciones.
PLANO PARALELOAUNARECTAQUE CONTENGAAOTRARECTA
Para trazar un plano, que contenga a una recta, paralelo a otra recta, se toma un punto cualquiera
de la primera y se traza una recta paralela a la segunda, el plano definido por las rectas que se
cortan es la solución.

Recta perpendicular a un plano por un punto.
Plano perpendicular a una recta por un
punto.
V
V
2
1
b A a
2 2 2
A
1
b
Plano que contiene una recta perpendicular a
otro.
H
a2
b
V A
1 2
2
a 1
H V H a
2 1 2 1
1
a 1
A b
2
1 1
H
a
1
1
A
2
A
1
PERPENDICULARIDAD
Recta perpendicular por un punto a
otra(frontal).
A
2
A b
1 1
b a
B
2 1
2
B a
1 1
Recta perpendicular por un punto a otra.
V
2
V A b
2 2
2
a2
B2
V V H
1 1 2
A
1
c
2
c
1
B b
1
1
a H
1 1
Plano perpendicular a otros dos por un
punto.
V
2
a
1
A b V
V H V
a b
A
H
2 2 2
1 2 1
1 1
1
1

PERPENDICULARIDAD
Una recta es perpendicular a un plano cuando lo es a dos rectas del plano que pasen por el punto común
de intersección.
Los planos perpendiculares a una recta son paralelos entre sí.
Un plano es perpendicular a otro cuando el primero contiene una recta perpendicular al segundo.
Un plano perpendicular a la recta de intersección de dos planos lo es también a ellos.
Por un punto se pueden trazar infinitos planos perpendiculares a un plano, tantos como infinitos son los
que pasan por la recta perpendicular trazada al plano por el punto.
Por una recta, no perpendicular a un plano, sólo pasa un plano perpendicular a éste.
CASOS DE PERPENDICULARIDAD
PERPENDICULARIDAD ENTRE RECTAYPLANO
Una recta es perpendicular a un plano cuando las proyecciones de esta son perpendiculares a las trazas
homónimas del plano.
RECTAPERPENDICULARAUN PLANO POR UN PUNTO
Basta con trazar, por las proyecciones del punto, perpendiculares a las trazas homónimas del
plano.
PLANO PERPENDICULARAUNARECTAPOR UN PUNTO
Se contiene el punto en una recta notable (horizontal o frontal) de forma que la proyección de
ésta, no paralela a la línea de tierra, sea perpendicular a la recta dada. El plano definido por la
recta notable es la solución.
PERPENDICULARIDAD ENTRE RECTAYRECTA
En general las proyecciones de dos rectas perpendiculares en el espacio son dos rectas oblicuas.
Solamente cuando una de las dos rectas, perpendiculares en el espacio, es paralela a uno de los planos de
proyección, las proyecciones de ambas, sobre este plano aparecen perpendiculares.
RECTAPERPENDICULARAOTRAPOR UN PUNTO
Para trazar una recta perpendicular a otra por un punto, hay que contener el punto en una recta
notable (horizontal o frontal) que defina el plano perpendicular a la recta dada. Hallar el punto
de intersección del plano con la recta. La unión de los dos puntos es la solución.
PERPENDICULARIDAD ENTRE PLANOYPLANO
ENTRE RECTAYPLANO y viceversa.
ENTRE RECTAYRECTA
ENTRE PLANOYPLANO
ENTRE PLANOYDOS PLANOS
PLANO PERPENDICULARAOTRO PLANO POR UN PUNTO
Se traza por el punto una recta perpendicular al plano dado. El plano cuyas trazas contengan a
las de la recta será la solución.
PLANO PERPENDICULARAOTRO POR UNARECTA
Se traza, por un punto cualquiera de la recta, otra recta perpendicular al plano dado. El plano que
definen las rectas que se cortan es la solución.
PERPENDICULARIDAD ENTRE PLANOYDOS PLANOS
PLANO PERPENDICULARAOTROS DOS PLANOS POR UN PUNTO
Al hallar la recta de intersección de los planos, reducimos el problema a trazar por un punto un
plano perpendicular a una recta, ya visto.

h
a
a’
a 1
Distancia (magnitud real) entre dos puntos.
z
Distancia de un punto a un plano.
A
A
2
1
A
0
V
2
a
B A
b
V A H
a
2
2 2
1 1 1
1
a
B
1
b
1
2
B
a B
a
2
1 1
Distancia entre dos planos paralelos.
0
2
H
V2
a2
V2 B2
A2
b2
V V c H
1 1 2 2
b1 A1
c1
B1 H
1 a H
1 1
1
DISTANCIAS
Distancia entre dos rectas paralelas.
V
a
2
b V
A
2 2
1 1
2
c
d
2
H H V V
a1
A1 b1
H1
d
B1
c H
2
B 2
2 2 1 1
Distancia entre dos rectas que se cruzan, una
de ellas vertical.
c2
a2 B2 A2
b
Distancia entre dos rectas que se cruzan.
V
2
V d
e a
2 2
2 2
g f b
C V c
B2 E2
V V E H V H
H2
B
D1 f g
A1
a
C c H
b d
H
2 2 2
2 2 2
1 1 1 2 1 2
1 1 1 1
1 1 1
1 1
a A
b1
B c
1
1 1
1 1
H
1
1
2
2

DISTANCIAS
Consiste en hallar la distancia real (verdadera magnitud) medida en el espacio entre dos puntos,
independientemente de los casos concretos que se exponen.
Los problemas de distancias están relacionados con temas anteriores (...intersecciones, paralelismo,
perpendicularidad) y será necesario su conocimiento para resolverlos.
CASOS DE DISTANCIAS
DISTANCIAENTRE DOS PUNTOS
DISTANCIADE UN PUNTOAUN PLANO
DISTANCIAENTRE DOS PLANOS PARALELOS
DISTANCIAENTRE RECTAS PARALELAS
DISTANCIADE UN PUNTOAUNARECTA
ENTRE DOS PUNTOS
DE UN PUNTOAUN PLANO
ENTRE DOS PLANOS PARALELOS
ENTRE DOS RECTAS PARALELAS
DE UN PUNTOAUNARECTA
ENTRE DOS RECTAS QUE SE CRUZAN
En el caso de que los dos puntos tengan idéntica medida de cota o de alejamiento, la verdadera magnitud
entre ellos será la proyección sobre el plano al cual es paralelo el segmento que los une..
Cuando la unión de los dos puntos da un segmento oblicuo, su verdadera magnitud se halla
construyendo un triángulo rectángulo:
Hipotenusa, verdadera magnitud.
Cateto (1), distancia entre cotas o entre alejamientos.
Cateto (2), proyección horizontal o proyección vertical.
La distancia de un punto a un plano la da el segmento perpendicular trazado desde el punto hasta su
intersección con el plano.
La distancia entre dos planos paralelos es la unión de los dos puntos de intersección de una recta
perpendicular a ambos planos.
La distancia entre dos rectas paralelas es el segmento que une los dos puntos de intersección de un plano
perpendicular a dichas rectas.
La distancia de un punto a una recta es el segmento que une dicho punto con el de intersección de un
plano que, pasando por el punto, sea perpendicular a la recta.
DISTANCIAENTRE DOS RECTAS QUE SE CRUZAN
La distancia entre dos rectas que se cruzan es el segmento que une los puntos de intersección de una
recta perpendicular trazada a las dos rectas.

A A B
B
A
(A )
PH
ABATIMIENTOS
0 1 0
0
A
Abatimiento de una recta horizontal del
plano.
V A a
V
2 2 2
1
A
0
a
0
A
1
1
z
(A 0)
B a
1 1
Abatimiento de una figura plana contenida
en un plano.
A a
A
2 2
1
C
2
a
1
B
C V
B0
C
A
2
1 0
0
0
B 1
V
V
2
1
z
a
0
Abatimiento de un punto del plano.
V A a
V
A
2 2 2
1
0
A
1
z
z
(A 0)
B a
1 1
Abatimiento de una recta y del plano.
V
0
V
V
1
2
A
A
2
1
a
a
H
A a H
H
0 0 1
Abatimiento de una figura plana contenida
en un plano.
V B
0 0
V 2
a
2
B
2
A
C2
V H
1 2
B
A
0
1
C a
C
0 0
1
a
1
2
2
H
1
1
A
2
1
0

ABATIMIENTOS
Método para obtener la verdadera magnitud de líneas y figuras planas, así como su forma.
Abatir un plano y todo lo que este contiene (puntos, rectas y figuras planas) sobre uno de los planos de
proyección consiste en girarlo alrededor de una recta de intersección de ambos, llamada eje de
abatimiento o charnela (bisagra), hasta hacerlo coincidir con él.
En los abatimientos se tendrá en cuenta: el plano a abatir, el eje (charnela) y la dirección de abatimiento.
Afinidad. Correspondencia entre dos figuras, de modo que a cada punto de la primera le corresponde
un único punto de la segunda, concurriendo cada recta con su afín en un punto de la recta fija llamada eje
de afinidad (charnela o bisagra).
La línea que une dos puntos afines define la dirección de afinidad, así pues, todo punto tendrá su afín en
una paralela a la dirección de afinidad.
Elementos de la afinidad en diédrico:
Eje de afinidad (charnela): Recta de intersección del plano de proyección (PH o PV) y del que
contiene la figura.
Dirección de afinidad: Perpendicular a la recta de intersección (eje de afinidad).
Par de puntos afines: Proyección del punto (horizontal/vertical) y su abatimiento.
CASOS DEABATIMIENTO DE UN PUNTO DE UN PLANO
DE UN PLANO
DE UNARECTADE UN PLANO
DE UNAFIGURAPLANACONTENIDAEN UN PLANO
ABATIMIENTO DE UN PUNTO DE UN PLANO
Al abatir, el punto situado en el plano describirá un arco de circunferencia, contenido en un plano
perpendicular al eje de abatimiento.
Nos basaremos en tres segmentos que forman un triángulo rectángulo para efectuar el abatimiento:
Cateto (1) Distancia del punto hasta su proyección.
Cateto (2) Distancia perpendicular desde la proyección del punto hasta su intersección con el eje
de abatimiento.
Hipotenusa Segmento que une los extremos libres de los dos catetos.
La correspondencia, en diédrico, de los tres lados del triángulo rectángulo queda de la siguiente forma,
si se quiere abatir sobre el plano horizontal. Para abatir sobre el vertical se actúa de la misma forma
teniendo en cuente la correspondencia entre los elementos.
Cateto (1) Distancia de cota del punto.
Cateto (2) Segmento perpendicular que une la proyección horizontal con la traza del plano (eje de
abatimiento o charnela).
Hipotenusa Segmento que une los extremos libres de los dos catetos. Esta medida, situada en la
perpendicular trazada por la proyección del punto al eje de abatimiento y a partir de éste
situará el punto abatido.
ABATIMIENTO DE UN PLANO
Consiste en abatir la superficie, entre las dos trazas, del plano correspondiente al primer diedro.
Una de las trazas servirá como eje de abatimiento y un punto de la otra nos dará su situación al abatirlo.
El caso se resuelve como si tuviésemos que abatir un punto del plano, aunque se puede basar en otro
triángulo rectángulo formado por las trazas y una recta de máxima pendiente (o máxima inclinación).
Cateto Distancia desde la proyección horizontal, de la traza horizontal de una recta de máxima
pendiente, hasta la convergencia de las trazas del plano en la línea de tierra.
Cateto Verdadera magnitud del segmento de la recta de máxima pendiente entre las dos trazas.
Hipotenusa Distancia desde la proyección vertical, de la traza vertical de la recta de máxima
pendiente, hasta la convergencia de las trazas del plano en la línea de tierra.
ABATIMIENTO DE UNARECTADE UN PLANO
Una vez abatido un punto cualquiera de la recta, se une con el de intersección de la proyección de la
recta y la traza del plano. (Afinidad)
ABATIMIENTO DE UNAFIGURAPLANACONTENIDAEN UN PLANO
Si abatimos la traza, por el método de las rectas notables, si se abate un punto, por afinidad.

A
2
PV
PV’
A
A
1
PH
Recta oblicua convertida en frontal mediante
un cambio de plano (vertical).
PV
A
2
A’ B’
2 2
A
1
Convertir un plano oblicuo en proyectante
horizontal (plano vertical) mediante un
cambio de plano (horizontal).
B’
1
’
1
’
2
B
B
2
1
A A
1 2
B
1
A’
CAMBIOS DE PLANO
2
PH
El punto en el cambio de plano (vertical).
PV
A
A
2
z
Recta frontal convertida en vertical mediante
un cambio de plano (horizontal).
A
2
B
A B
1 1
2
z
A’
2
PH
A’ 1
B’
Convertir un plano oblicuo en proyectante
vertical (de canto) mediante un cambio de
plano (vertical).
PV
B
2
A A
2 1
’
1
’
B’
2
2
2

CAMBIOS DE PLANO
Consiste en elegir otros planos de proyección o modificar su posición, de forma que los elementos a
proyectar adquieran una nueva situación (de perpendicularidad o paralelismo) más favorable en la
resolución del problema.
Se pueden efectuar los cambios necesarios pero siempre de uno en uno.
DETERMINACIÓN DE LANUEVALÍNEADE TIERRA
Al efectuar un cambio de plano, la recta de intersección (nueva línea de tierra) se sitúa en la posición
deseada y con dos trazos en los extremos; para los siguientes cambios de plano se van aumentando los
trazos de los extremos.
Además, para saber el plano elegido en el cambio se indicará mediante las letras V y H (Vertical u
Horizontal de proyección), situándolas en los extremos de la línea de tierra y con el subíndice
correspondiente a dicho cambio.
DESIGNACIÓNYPOSICIÓN DE LAS NUEVAS PROYECCIONES
Las nuevas proyecciones se indicarán con una, dos, tres... comillas, correspondientes al mismo número
del cambio efectuado.
CAMBIO DELPLANO VERTICAL
Cuando se modifica el plano vertical, la proyección horizontal mantiene la misma situación y, después
de trazar la línea de correspondencia, se lleva sobre ella la proyección vertical con la medida de cota
correspondiente.
CAMBIO DELPLANO HORIZONTAL
En caso de modificar el plano horizontal, la proyección vertical permanece en la misma situación,
llevando la medida del alejamiento sobre la nueva línea de correspondencia.
ELPUNTO EN ELCAMBIO DE PLANO
El interés de este cambio del plano tiene su justificación sólo si se va a modificar la cota, el alejamiento
del punto o cambiar su situación respecto a los planos de proyección (diedro, semiplanos...) y se tendrán
en cuenta los convencionalismos al efectuar los cambios de planos.
LARECTAEN ELCAMBIO DE PLANO
Consistirá, generalmente, en situar la recta paralela o perpendicular a los planos de proyección.
Para modificar la posición de una recta mediante un cambio de plano hay que obtener las nuevas
proyecciones de dos de sus puntos.
ELPLANO EN ELCAMBIO DE PLANO
Obtener una nueva disposición del plano frente a los de proyección, convirtiéndolo en proyectante o
paralelo, y conseguir que los elementos contenidos en él o relacionados adquieran una posición más
favorable de trabajo.
Al efectuar un cambio de plano para modificar la disposición de un plano cualquiera, se tendrá en
cuenta el punto de intersección de las líneas de tierra, ya que el punto de la traza del plano que tiene su
proyección coincidente con el de las rectas será el que, una vez efectuado el cambio, indicará por donde
debe pasar la nueva traza del plano.

GIROS
A’ A’
e2
e
A A’
A
A
2
2 1
1
Giro de un segmento oblicuo a la posición de
frontal mediante un eje vertical.
A A’
e
2 2
e
1
B B’
A B B’
2
2 2
1 1 1
e A’
1 1
Giro de un plano oblicuo a la posición de
canto mediante un eje vertical.
1
’
2
e
A
C
B C B’
e1
A B’
B
1
2
2
2 1 2
2
1 1
’
Giro de un punto mediante un eje vertical y
otro de punta.
A A’
2 2
A
1
B
2
A
2
Giro de un plano a proyectante horizontal
mediante un eje de punta.
e
1
e e’
2 2
B’
e A’
e
2 2
B B’
1
1
1 1
B
2
’
A A’
1 1
e
2
’
B A B’
1 2 2
e
1
A
1
e’
1
A’ A”
1 1
Giro de una recta oblicua a la posición de
perfil mediante un eje de punta.
2
2
A”
2

GIROS
Los giros permiten situar los elementos representados en una posición que favorece la resolución de
problemas.
En los giros se modifica el elemento representado manteniendo fijos los planos de proyección.
Se realizan tomando una recta vertical o de punta como ejes de rotación y relacionando el elemento a
girar con dicho eje, alrededor del cual describirá una circunferencia.
La proyección del eje que queda perpendicular a la línea de tierra debe terminar en punta de flecha
(convencionalmente) para distinguirla de las rectas.
Al efectuar un giro hay que tener en cuenta: El eje de giro.
Perpendicular al horizontal. (Eje recta vertical)
Perpendicular al vertical. (Eje recta de punta)
El elemento a girar.
La amplitud del ángulo de giro.
El sentido del giro.
CASOS DE GIROS
GIRO DE UN PUNTO
DE UN PUNTO
DE UNARECTAO UN SEGMENTO
DE UNASUPERFICIE O UN PLANO
DE UN VOLUMEN (*)
Para girar un punto mediante un eje vertical, se traza una circunferencia con centro en la proyección
horizontal del eje y radio hasta la proyección horizontal del punto.
Una vez fijada la nueva posición de la proyección horizontal del punto, se traza la línea de
correspondencia trasladando la otra proyección paralela a la línea de tierra hasta ella.
Si el giro se efectúa con un eje de punta, el procedimiento es el mismo pero intercambiando las
proyecciones.
GIRO DE UNARECTAO DE UN SEGMENTO
Cuando el eje y la recta se cortan, basta con girar un punto cualquiera de la recta. Cuando el eje y la recta
se cruzan, hay que relacionar perpendicularmente el eje con la recta y mantener dicha
perpendicularidad en la nueva posición.
GIRO DE UNASUPERFICIE O DE UN PLANO
Igual que en el giro de una recta, hay que relacionar el eje y la traza del plano perpendicularmente y fijar
la nueva posición teniéndolo en cuenta.
Para situar la otra traza del plano se necesita conocer un punto de ella y, una vez girado, unirlo con el de
intersección de la primera en la línea de tierra.
GIRO DE UN VOLUMEN (*)
En intersecciones de planos y figuras es conveniente esta aplicación para solucionar el ejercicio más
fácilmente.