Una construcción del centro de curvatura en cónicas - Geometría
Una construcción del centro de curvatura en cónicas - Geometría
Una construcción del centro de curvatura en cónicas - Geometría
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
C<strong>en</strong>tro <strong>de</strong> <strong>curvatura</strong> <strong>en</strong> <strong>cónicas</strong><br />
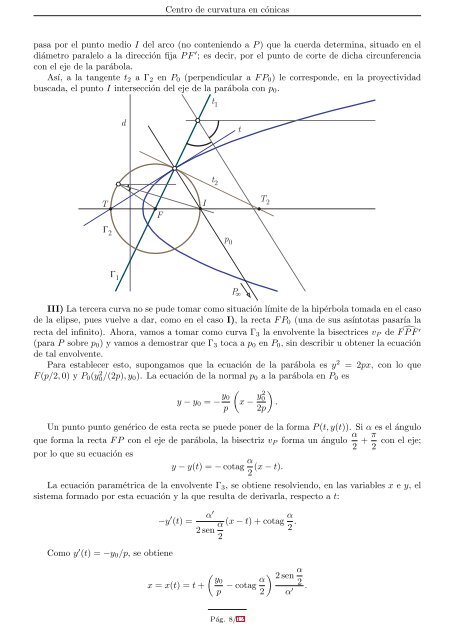
pasa por el punto medio I <strong><strong>de</strong>l</strong> arco (no cont<strong>en</strong>i<strong>en</strong>do a P ) que la cuerda <strong>de</strong>termina, situado <strong>en</strong> el<br />
diámetro paralelo a la dirección fija P F ′ ; es <strong>de</strong>cir, por el punto <strong>de</strong> corte <strong>de</strong> dicha circunfer<strong>en</strong>cia<br />
con el eje <strong>de</strong> la parábola.<br />
Así, a la tang<strong>en</strong>te t2 a Γ2 <strong>en</strong> P0 (perp<strong>en</strong>dicular a F P0) le correspon<strong>de</strong>, <strong>en</strong> la proyectividad<br />
buscada, el punto I intersección <strong><strong>de</strong>l</strong> eje <strong>de</strong> la parábola con p0.<br />
III) La tercera curva no se pu<strong>de</strong> tomar como situación límite <strong>de</strong> la hipérbola tomada <strong>en</strong> el caso<br />
<strong>de</strong> la elipse, pues vuelve a dar, como <strong>en</strong> el caso I), la recta F P0 (una <strong>de</strong> sus asíntotas pasaría la<br />
recta <strong><strong>de</strong>l</strong> infinito). Ahora, vamos a tomar como curva Γ3 la <strong>en</strong>volv<strong>en</strong>te la bisectrices vP <strong>de</strong> F P F ′<br />
(para P sobre p0) y vamos a <strong>de</strong>mostrar que Γ3 toca a p0 <strong>en</strong> P0, sin <strong>de</strong>scribir u obt<strong>en</strong>er la ecuación<br />
<strong>de</strong> tal <strong>en</strong>volv<strong>en</strong>te.<br />
Para establecer esto, supongamos que la ecuación <strong>de</strong> la parábola es y 2 = 2px, con lo que<br />
F (p/2, 0) y P0(y 2 0/(2p), y0). La ecuación <strong>de</strong> la normal p0 a la parábola <strong>en</strong> P0 es<br />
y − y0 = − y0<br />
p<br />
<br />
x − y2 <br />
0<br />
.<br />
2p<br />
Un punto punto g<strong>en</strong>érico <strong>de</strong> esta recta se pue<strong>de</strong> poner <strong>de</strong> la forma P (t, y(t)). Si α es el ángulo<br />
que forma la recta F P con el eje <strong>de</strong> parábola, la bisectriz vP forma un ángulo α π<br />
+ con el eje;<br />
2 2<br />
por lo que su ecuación es<br />
y − y(t) = − cotag α<br />
(x − t).<br />
2<br />
La ecuación paramétrica <strong>de</strong> la <strong>en</strong>volv<strong>en</strong>te Γ3, se obti<strong>en</strong>e resolvi<strong>en</strong>do, <strong>en</strong> las variables x e y, el<br />
sistema formado por esta ecuación y la que resulta <strong>de</strong> <strong>de</strong>rivarla, respecto a t:<br />
Como y ′ (t) = −y0/p, se obti<strong>en</strong>e<br />
−y ′ (t) = α′<br />
2 s<strong>en</strong> α (x − t) + cotag<br />
2<br />
α<br />
2 .<br />
x = x(t) = t +<br />
y0<br />
p<br />
− cotag α<br />
2<br />
Pág. 8/12<br />
α<br />
2 s<strong>en</strong><br />
2<br />
α ′ .