problema sobre vibraciones - MecFunNet

1. Oscilaciones 1
(Puede ver una animación)
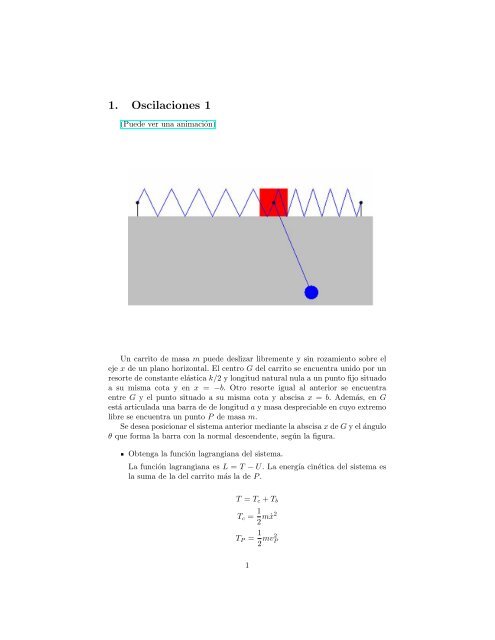
Un carrito de masa m puede deslizar libremente y sin rozamiento sobre el
eje x de un plano horizontal. El centro G del carrito se encuentra unido por un
resorte de constante elástica k/2 y longitud natural nula a un punto fijo situado
a su misma cota y en x = −b. Otro resorte igual al anterior se encuentra
entre G y el punto situado a su misma cota y abscisa x = b. Además, en G
está articulada una barra de de longitud a y masa despreciable en cuyo extremo
libre se encuentra un punto P de masa m.
Se desea posicionar el sistema anterior mediante la abscisa x de G y el ángulo
θ que forma la barra con la normal descendente, según la figura.
Obtenga la función lagrangiana del sistema.
La función lagrangiana es L = T − U. La energía cinética del sistema es
la suma de la del carrito más la de P .
T = T c + T b
T c = 1 2 mẋ2
T P = 1 2 mv2 P
1

Para calcular v P se hace
x P = x + a sen θ ⇒ ẋ c = ẋ + a ˙θ cos θ
con lo que
de modo que
y P = −a cos θ ⇒ ẏ c = a ˙θ sen θ
v 2 P = ẋ 2 + a 2 ˙θ2 + 2aẋ ˙θ cos θ
T = 1 2 mẋ2 + 1 (ẋ
2 m 2 + a 2 ˙θ2 + 2aẋ ˙θ
)
cos θ
El potencial queda
con lo que
T = 1 (2ẋ
2 m 2 + a 2 ˙θ2 + 2maẋ ˙θ
)
cos θ
U = −mga cos θ + 1 2 kx2
L = 1 (2ẋ
2 m 2 + a 2 ˙θ2 + 2maẋ ˙θ
)
cos θ + mga cos θ − 1 2 kx2
Obtenga las posiciones de equilibrio del sistema
Al aplicar las ecuaciones de Lagrange se tiene
2mẍ + 2ma d( ˙θ cos θ)
dt
= −kx
ma 2 d(ẋ cos θ)
¨θ + 2ma = −mga sen θ
dt
y existe una posición de equilibrio estable en x = 0; θ = 0 y otra inestable
en x = 0; θ = π.
Linealice las ecuaciones diferenciales que rigen la evolución del sistema en
torno al punto de equilibrio estable.
2mẍ + ma¨θ = −kx
ma 2 ¨θ + maẍ = −mgaθ
Encuentre las frecuencias de vibración para la posición de equilibrio estable
con los valores m = 1kg, a = 1m, g = 10ms −2
Al sustituir soluciones del tipo
x = A 1 cos ωt
θ = A 2 cos ωt
2

se tiene
−(2mA 1 + maA 2 )ω 2 + kA 1 = 0
−(ma 2 A 2 + maA 1 )ω 2 + mgaA 2 = 0
Sistema que sólo admite soluciones no triviales si
k
∆ =
m
∣
− ∣ 2ω2 −aω 2 ∣∣∣
−aω 2 ga − a 2 ω 2 = 0
Si se hace m = 1kg, a = 1m, g = 10ms −2 entonces se tiene en el S.I.
∆ =
∣ k − ∣ 2ω2 −ω 2 ∣∣∣
−ω 2 10 − ω 2 = 0
lo que proporciona las pulsaciones
ω 2 = 10 + k 2 ± √ 100 + k2
4
Describa los modos normales de oscilación del sistema.
De la primera ecuación del sistema, se tiene
A 2 = − 20 ± √ k 2 + 400
ω 2 A 1
Por lo que el primer modo de oscilación corresponde a vibraciones del tipo
y el segundo modo se expresa por
x(t) = A 1 cos ω 1 t
θ(t) = − 20 + √ k 2 + 400
ω 2 A 1 cos ω 1 t
x(t) = A 1 cos ω 2 t
θ(t) = − 20 − √ k 2 + 400
ω 2 A 1 cos ω 1 t
Obtenga las pulsaciones si se hace k = 10N/m.
Entonces
ω 1 = 5, 11s −1
ω 2 = 1, 95s −1
3