2.6. Integral de superficie de un campo escalar.
2.6. Integral de superficie de un campo escalar.
2.6. Integral de superficie de un campo escalar.
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
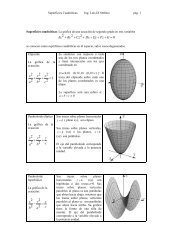
<strong>2.6.</strong> <strong>Integral</strong> <strong>de</strong> <strong>superficie</strong> <strong>de</strong> <strong>un</strong> <strong>campo</strong> <strong>escalar</strong>.Para <strong>de</strong>finir la integral <strong>de</strong> <strong>superficie</strong> <strong>de</strong> <strong>un</strong> <strong>campo</strong> <strong>escalar</strong>, consi<strong>de</strong>raremos <strong>un</strong>a <strong>superficie</strong>S que esta dada paramétricamente por la f<strong>un</strong>ción vectorial g, <strong>de</strong>finida por( ) ( ( ) ( ) ( )) ( )2 3g: / g uv , xuv , , y uv , , z uv , xyz , ,R →R = = cuyas primeras <strong>de</strong>rivadasparciales son continuas, y tal que z ≥ 0 en toda <strong>un</strong>a región R <strong>de</strong>l plano uv, y sea laf<strong>un</strong>ción f ( , , )xyz <strong>un</strong>a f<strong>un</strong>ción <strong>escalar</strong> continua en toda la región3D ⊆R que contienea la <strong>superficie</strong> S. Entonces si <strong>de</strong>notamos por∆ Tiy Si∆ a las áreas <strong>de</strong> las regiones en elplano tangente y en la <strong>superficie</strong> S, respectivamente, obtenidas al proyectar la región Rien el plano tangente y en la <strong>superficie</strong> S en el p<strong>un</strong>to genéricoi( i, i, ( i,i))ahora la imagen <strong>de</strong> la f<strong>un</strong>ción f para el p<strong>un</strong>toi( i, i, ( i,i))el áreaP x y f x y . SiP x y f x y , se multiplica esta por∆ Ti<strong>de</strong> la proyección <strong>de</strong> la región R ien el plano tangente, y se realiza esteprocedimiento para todos los p<strong>un</strong>tos sobre la <strong>superficie</strong> se genera la siguiente sumanf x , y , z ∆ T + f x , y , z ∆ T + ... + f x , y , z ∆ T = f x, y , z ∆T( ) ( ) ( ) ( )1 1 1 1 2 2 2 2∑n n n n i i i ii=1Figura XX. <strong>Integral</strong> Campo EscalarDon<strong>de</strong> al tomar el límite <strong>de</strong> esta suma <strong>de</strong> Riemann cuando n →∞ se <strong>de</strong>fine la integral<strong>de</strong> <strong>superficie</strong> <strong>de</strong> la siguiente manera,Definición. Sea f <strong>un</strong>a f<strong>un</strong>ción <strong>escalar</strong> continua en <strong>un</strong>a región3D ⊆R que contiene a la<strong>superficie</strong> S, tal que S viene dada paramétricamente por la f<strong>un</strong>ción vectorial
( ) ( ( ) ( ) ( ))2 3g: / g u, v x u, v , y u, v , z u,vR →R = , entonces la integral <strong>de</strong> Superficie <strong>de</strong>f sobre la <strong>superficie</strong> S es∫∫Snf xyzdS , , = Lim f x, y,z ∆T∑( ) ( )n→∞ i = 1i i i iEl área <strong>de</strong> la <strong>superficie</strong> S si ésta viene dada en forma paramétrica <strong>de</strong> la forma( ) ( ( ))2 3h: / h x, y x, y, g x,yR →R = , se <strong>de</strong>termina a partir <strong>de</strong>∫∫( ) ⎤2⎡ ( ) ⎤2A= ⎡⎣gxx, y ⎦ + ⎣gyx, y ⎦ + 1dARY por tanto la evaluación <strong>de</strong> <strong>un</strong>a integral <strong>de</strong> <strong>superficie</strong> se pue<strong>de</strong> realizar a través <strong>de</strong> lasiguiente fórmula:S( ) ( )∫∫ ∫∫( ) ⎡ ( ) 2⎡ ( ) ⎤2x⎤yf xyzdS , , = f xyg , , xy , ⎣g xy , ⎦ + ⎣g xy , ⎦ + 1dARxySi la <strong>superficie</strong> S viene dada en forma paramétrica <strong>de</strong> la forma( ) ( ( ) ( ) ( ))2 3g: / g u, v x u, v , y u, v , z u,vR →R = , se <strong>de</strong>be recordar que el área <strong>de</strong> la<strong>superficie</strong> S viene dada por la integral doble( )( )( )( )( )( )2 2 2⎡∂ xy , ⎤ ⎡∂ yz , ⎤ ⎡∂xz , ⎤A = ∫∫ ⎢ ⎥ + ⎢ ⎥ + ⎢ ⎥ dudv∂ uv , ∂ uv , ∂ uv ,R ⎣ ⎦ ⎣ ⎦ ⎣ ⎦Y por tanto la evaluación <strong>de</strong> la integral <strong>de</strong> <strong>superficie</strong> se pue<strong>de</strong> realizar a través <strong>de</strong> lasiguiente fórmula:( )( )( )( )( )( )2 2 2⎡∂ xy , ⎤ ⎡∂ yz , ⎤ ⎡∂xz , ⎤f ( xyzdS , , ) = f( g1( uv , ), g2( uv , ), g3( uv , ))+ +dA⎢⎣∂ uv , ⎥⎦ ⎢⎣∂ uv , ⎥⎦ ⎢⎣∂uv , ⎥⎦∫∫ ∫∫S R uvLa interpretación física <strong>de</strong> la integral <strong>de</strong> la f<strong>un</strong>ción f sobre la <strong>superficie</strong> S <strong>de</strong>pen<strong>de</strong>rá <strong>de</strong>lsignificado físico que tenga la f<strong>un</strong>ción f, si la f<strong>un</strong>ción f ( , , )xyz representa la <strong>de</strong>nsidadsuperficial <strong>de</strong> la <strong>superficie</strong>, entonces la integral <strong>de</strong> f sobre S constituye la masa total <strong>de</strong>la lamina curvada.2 2EJEMPLO 52. Determine el valor <strong>de</strong> la siguiente integral <strong>de</strong> <strong>superficie</strong> ∫∫ ( x + y ) dS ,2 2don<strong>de</strong> S es la porción <strong>de</strong>l paraboloi<strong>de</strong> z = 4 −x − y que se encuentra sobre el plano xy.S
Solución. Una parametrización para esta <strong>superficie</strong>, dada <strong>de</strong> manera explicita, está dadapor la f<strong>un</strong>ción vectorial : 2 3 / ( , )0≤ y ≤ 2.⎡ x ⎤ ⎡x⎤g R →R g x y =⎢y⎥ ⎢y⎥⎢ ⎥=⎢ ⎥, con x2 + y2 ≤ 4 y2 2⎢⎣ 4 −x − y ⎥⎦ ⎢⎣z⎥⎦Al sustituir esta parametrización en el <strong>campo</strong> <strong>escalar</strong> g, la integral <strong>de</strong> <strong>superficie</strong> queda<strong>de</strong>finida por la siguiente expresión∫∫S2( ) ( ( )) ⎡x( ) ⎤ ⎡y( )∫∫f x, y, z dS = f x, y, f x, y ⎣g x, y ⎦ + ⎣g x, y ⎤⎦ + 1dARxy2 2∫∫ ( ) [ ] [ ]∫∫ ( )2 2= x + y − 2x + − 2y + 1dARxy= + + +R2 2 2 2x y 4x 4y 1dA∫ (0 ∫02 2 2 2) [ ] [ ]2π2∫ ∫2π2 2 2= r cos θ + r sen θ 2r cosθ + 2rsenθ + 1rdrdθ2 3= 4r+ 1r drdθ0 032π⎡ 1 2 2⎤= ∫ ( 4 1) ( )2 6 10⎢ r + r − ⎥ dθ⎣120⎦ 0⎛391 17 −1⎞=⎜π60 ⎟⎝ ⎠Al resolver la integral, en este caso es apropiado, realizar <strong>un</strong> cambio en coor<strong>de</strong>nadaspolares <strong>de</strong>bido a la región R que proyecta la <strong>superficie</strong> sobre el plano xy, en <strong>un</strong> discocircular don<strong>de</strong> se observa que 0≤r≤ 2 y 0≤θ≤ 2π.22Figura 57. Paraboloi<strong>de</strong> <strong>de</strong>l Ejemplo 52.
∫∫ y dS ,EJEMPLO 53. Determine el valor <strong>de</strong> la siguiente integral <strong>de</strong> <strong>superficie</strong> ( x + )don<strong>de</strong> S es la parte <strong>de</strong>l plano z = 4x+ ysobre la región limitada poryS2= x e 1y = .Solución. Para este plano <strong>un</strong>a parametrización conveniente está dada por⎡ x ⎤ ⎡x⎤2 3g: R →R / g( x,y)=⎢y⎥ ⎢y⎥⎢ ⎥=⎢ ⎥, con 0≤ x ≤ 1 y x2 ≤ y ≤ 1. La integral <strong>de</strong>⎢⎣4x + y⎥⎦ ⎢⎣z⎥⎦<strong>superficie</strong> en términos da las variables x e y está <strong>de</strong>finida por la expresión∫∫S( ) ( )2( ) ⎡x( ) ⎤ ⎡y( )f xyzdS , , = f xyf , , xy , ⎣g xy , ⎦ + ⎣g xy , ⎦⎤ + 1dARxy∫∫ ( ) [ ] [ ]1 102x( )2 2= x+ y 4 + 1 + 1dARxy= x + y 18dydx21⎡y ⎤= 18∫⎢xy+2⎥ dx⎣ ⎦1⎛= ∫ ⎜ + − + ⎟0⎝ 2 2 ⎠12 4 5⎡x 1 x x ⎤= ⎢ + x − +2 2 4 10⎥⎣⎦=∫∫∫∫172002x41 3 x ⎞x x dx102Figura 58. Superficie <strong>de</strong>l Ejemplo 53.EJERCICIOS PROPUESTOS <strong>2.6.</strong>
1) Determine la integral ( + + )∫∫S2x+ 2y+ z = 2 que se encuentra en el primer octante.2 22) Determine la integral ∫∫ ( + )2 2 2x + y + z = 4 con z ≥ 1.x y z dS, siendo la <strong>superficie</strong> S la porción <strong>de</strong>l planoSx y zdS, si la <strong>superficie</strong> S está <strong>de</strong>finida por3) Determine la integral∫∫S1dS , si la <strong>superficie</strong> S está <strong>de</strong>finida porz− y+1z = x + y con 0≤ x ≤ 1 y 0≤ y ≤ 1.22 24) Determine la integral∫∫SxyzdS , si la <strong>superficie</strong> S está <strong>de</strong>finida por la parte <strong>de</strong>lcilindrox+ z = 4 en el primer octante, entre los planos y = 0 y y = 1.2 2<strong>2.6.</strong>1. Aplicaciones <strong>de</strong> la integral <strong>de</strong> <strong>superficie</strong> <strong>de</strong> <strong>un</strong> <strong>campo</strong> <strong>escalar</strong>.La aplicación directa que tiene la integral <strong>de</strong> <strong>superficie</strong> <strong>de</strong> <strong>un</strong> <strong>campo</strong> <strong>escalar</strong> es la<strong>de</strong>terminación <strong>de</strong> la masa <strong>de</strong> <strong>un</strong>a <strong>superficie</strong>, cuando el <strong>campo</strong> <strong>escalar</strong> representa la<strong>de</strong>nsidad superficial <strong>de</strong> la misma. Se observará ésta aplicación en los siguientesejemplos. Sin embargo, así como pue<strong>de</strong> ser calculada la masa <strong>de</strong> <strong>un</strong>a lámina curvadatambién pue<strong>de</strong> ser <strong>de</strong>terminado su momento <strong>de</strong> inercia y su centro <strong>de</strong> masa.EJEMPLO 54. Determine la masa total <strong>de</strong> la <strong>superficie</strong> dada por la parte superior <strong>de</strong> laesfera2 2 2 2x + y + z = a , si la <strong>de</strong>nsidad superficial <strong>de</strong> la misma, está dada por la f<strong>un</strong>ción2( , , ) xg x y z= , con a > 0Solución. Esta <strong>superficie</strong> esférica tiene <strong>un</strong>a parametrización <strong>de</strong>finida en coor<strong>de</strong>nadas2 3esféricas por la f<strong>un</strong>ción ( )( ϕ) cos( θ)( ) ( )cos( ϕ )⎡asen⎤ ⎡x⎤⎢ ⎥g: R →R / g θϕ , = asen ϕ sen θ⎢y⎥⎢ ⎥=⎢ ⎥⎢⎣ a ⎥⎦ ⎢⎣z⎥⎦en don<strong>de</strong>0≤θ≤ 2πy 0 ≤ϕ ≤ π . La integral <strong>de</strong> <strong>superficie</strong> que se va a a calcular esta dada por( , , ) ( 1( θϕ , ), 1( θϕ , ), 1( θϕ , ))∫∫ ∫∫f x y z dS = f g g g r × r dAS R xySe calcula el vector normal n que se <strong>de</strong>fine como n= r × r , y para ello se <strong>de</strong>terminanlos vectores tangentes r θy r ϕcomo se muestra a continuaciónθϕθϕ
ϕ⎛ ∂x ∂y ∂z⎞= ⎜ , , ⎟⎝∂ϕ ∂ϕ ∂ϕ⎠= −( a cos( ϕ ) cos ( θ) , a cos ( ϕ) sen( θ) , asen( ϕ))rθ⎛ ∂x ∂y ∂z⎞= ⎜ , , ⎟⎝∂θ ∂θ ∂θ⎠= −( asen( ϕ) sen( θ) , asen( ϕ) cos ( θ),0)El producto vectorial <strong>de</strong> estos vectores, el vector norma n, está dada por el siguientevector n r ( 2 2 cos , 2 2 s , 2θrϕ a sen ϕ θ a sen ϕ enθ a senϕcosθ)= × = − − − . Como nos interesaes la norma <strong>de</strong> este producto cartesiano, al calcularlo queda dado por2n = a senϕY al sustituir esta parametrización y realizar <strong>un</strong> cambio <strong>de</strong> variable apropiado se<strong>de</strong>sarrolla la integral <strong>de</strong> <strong>superficie</strong> correspondiente para <strong>de</strong>termina las masa <strong>de</strong> la láminaen forma <strong>de</strong> esfera.∫∫S( 1 1 1 )( , , ) ( θϕ , ), ( θϕ , ), ( θϕ , )f xyzdS= f g g g r×r dA=∫∫Rθϕ∫∫Rθϕ( s ( ) cos( ))π2π4 2 3 2∫ s0 ∫02 2a en ϕ θ a senϕ dϕdθ( ) cos ( )= a en ϕ θ dϕdθπ2π24 ⎡ 1 cos3 ⎤ cos2∫0⎢⎣ 3 ⎥⎦ 0( ) ( )= a ϕ+ϕ θ dθ24⎛π1 ⎞ π2= a ⎜ − ⎟ cos ( )2 3∫ θ dθ0⎝ ⎠4 ⎛π1⎞⎡1 1 ⎤= a ⎜ − θ + cos ( 2 θ)⎝ 2 3⎟⎢⎠⎣2 4 ⎦⎥4a 2= ( 3π−2π)6πComo 0 ≤ϕ≤ , entonces senϕ= senϕ; al resolver la integral, en este caso es2πapropiado, integrar sobre la región <strong>de</strong>l plano θ y ϕ en don<strong>de</strong> se observa que 0 ≤ϕ≤2y 0≤θ≤ 2π.4a62La masa <strong>de</strong> ésta <strong>superficie</strong> esférica es <strong>de</strong> ( 3π2π)2π− <strong>un</strong>ida<strong>de</strong>s.0θϕ
Figura 59. Superficie esférica <strong>de</strong>l Ejemplo 54.EJEMPLO 55. Determine la masa total <strong>de</strong> la <strong>superficie</strong> dada por la parte <strong>de</strong>l planoz = b+ y, que se encuentra <strong>de</strong>ntro <strong>de</strong>l cilindro2 2 2la misma, está dada por la f<strong>un</strong>ción g( x, y,z) x y z2 2 2x + y = b , si la <strong>de</strong>nsidad superficial <strong>de</strong>= + + , con b > 0Solución. Para esta <strong>superficie</strong> dada <strong>de</strong> manera explicita por la forma z f ( x,y)2 3parametrización está <strong>de</strong>finida por la f<strong>un</strong>ción : / ( , )0 ≤ x ≤ b y 0 y b= <strong>un</strong>a⎡ x ⎤ ⎡x⎤g R →R g x y =⎢y⎥ ⎢y⎥⎢ ⎥=⎢ ⎥, con⎢⎣ b+y⎥⎦ ⎢⎣z⎥⎦≤ ≤ . El vector normal <strong>de</strong> éste plano es ( 0, 1,1)n = − , cuya norman =2 . La integral <strong>de</strong> <strong>superficie</strong> correspondiente para <strong>de</strong>terminar el área <strong>de</strong> estalámina plana cuya <strong>de</strong>nsidad superficial no es homogénea sobre toda su <strong>superficie</strong> queda<strong>de</strong>finida como
∫∫S( )( , , ) = , , ( , )∫∫f x y z dS f x y f x y n dARxy∫∫2 22( ( ) )= x + y + b + y 2dxdyRxy2 2 2∫∫ ( )= x + 2y + 2by + b 2dxdyRxy(( ) ( ))2π2 2 2 2∫ ∫= 2 r cosθ + 2 rsenθ + 2brsenθ + b rdrdθ0 024 2 4 2 3 2 2⎤r r sen r sen b r d2π⎡1 1 1 1= ∫ cos ( ) ( ) ( )0 ⎢ θ + θ + θ + θ⎣4 2 3 2 ⎥⎦2π⎡ 2 2 2 1 2⎤= 4∫cos ( θ) 2sen ( θ) sen( θ)b dθ0 ⎢+ + +⎣3 2 ⎥⎦2π2 ⎤θ ( θ) θ ( θ) ( θ)b θ⎥⎦ 0⎡1 1 1 2 1= 4⎢+ cos 2 + − cos 2 − cos +⎣2 4 2 3 22( b )= 4π3+0Figura 60. Superficie S <strong>de</strong>l Ejemplo 55.EJERCIOS PROPUESTOS <strong>2.6.</strong>1.1) Determine la masa total <strong>de</strong> la <strong>superficie</strong> dada por la parte <strong>de</strong>l plano2bx + 3by + bz = 6b, que se encuentra en el primer octante, si la <strong>de</strong>nsidad superficial <strong>de</strong>la misma, está dada por la f<strong>un</strong>ción g ( x, y,z)= bx + by , con b > 02) Determine la masa total <strong>de</strong> la <strong>superficie</strong> dada por la parte <strong>de</strong>l paraboli<strong>de</strong>2 22z = x + y ,que se encuentra a<strong>de</strong>ntro <strong>de</strong>l cilindro2 22y = x + y , si la <strong>de</strong>nsidad superficial <strong>de</strong> la2 2 2misma, está dada por la f<strong>un</strong>ción g( x, y,z) = x + y + z
3) Determine la masa total <strong>de</strong> la <strong>superficie</strong> dada por la parte <strong>de</strong> la esfera2 2 2 2x + y + z = 4a, que se encuentra a<strong>de</strong>ntro <strong>de</strong>l cilindro2 22ax = x + y en el primeroctante, si la <strong>de</strong>nsidad superficial <strong>de</strong> la misma está <strong>un</strong>iformemente distribuida.