Enoncé et Corrigé

Devoir n˚5 page 1 de 2
I)
OAB est un triangle
1. Construire les points C et D définis par : −→ −→ −−→ −→
OC = 4OA et CD = 4AB D
C
A
2. En utilisant le relation de Chasles avec −→ −−→ −−→
−→
OC et CD, calculer OD en fonction de OB.
En déduire que O, B et D sont alignés.
−−→
OD = −→ −−→ −→ −→ −→
−−→
OC + CD = 4 OA + 4 AB = 4 OB , donc les vecteurs OD et
−→
OB sont colinéaires, donc les points O, B et D sont alignés.
II)
ABC est un triangle. I et J sont les points tels que −→ AI = 1 −→
AB et
3
−→
AJ = 3 −→
AC.
Faire un dessin.
J
C
A I
B
Démontrer que les droites (BJ) et (IC) sont parallèles de chacune des façons suivantes :
1. avec la réciproque du théorème de Thalès (pour cela on calculera des rapports de
longueurs, comme par exemple AI
AB )
B
O
Devoir n˚5
Durée : 2 heures. Calculatrices autorisées
Dans les triangles AIC et ABJ :
les points A, I, B sont alignés
les points A, C, J sont alignés dans le même ordre
AI 1 AC 1
= et = , donc, d’aprè la réciproque du théorème de Thalès, (CI) est
AB 3 AJ 3
parallèle à (BJ)
2. en établissant que −→
BJ = 3 −→
IC (pour cela, on pourra utiliser la relation de Chasles avec
−→
BA et −→
AJ).
−→
IC = −→
IA + −→
AC = − 1 −→
AB +
3
−→
AC
−→
BJ = −→ −→ −→ −→
BA + 3AC = −AB + 3AC Donc −→
BJ = 3 −→
IC. Cela prouve que −→
BJ et −→
IC sont colinéaires, donc les droites (BJ)
et (IC) sont parallèles.
III)
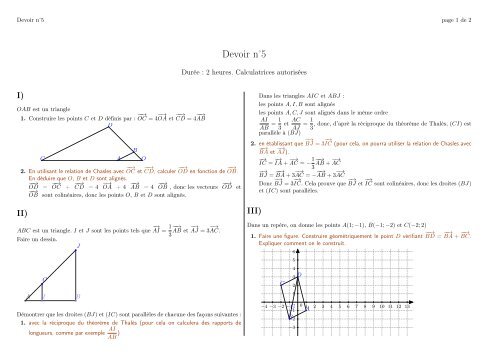
Dans un repère, on donne les points A(1; −1), B(−1; −2) et C(−2; 2)
1. Faire une figure. Construire géométriquement le point D vérifiant −−→
BD = −→ −→
BA + BC.
Expliquer comment on le construit.
C
6
5
4
3 D
2
1
−4 −3 −2 −1G −1
B−2
0 1
A
2 3 4 5 6 7 8 9 10 11 12 13
−3

Devoir n˚5 page 2 de 2
On trace un parallélogramme à partir de A, B et C : D est le quatrième sommet
du parallélogramme ABCD
2. Déterminer les coordonnées (xD; yD) du point D par le calcul.
L’égalité −−→
BD = −→ −→
BA + BC se traduit par
xD + 1 = 2 + (−1) xD = 0
d’où
yD + 2 = 1 + 4
yD = 3
Les coordonnées de D sont (0; 3)
3. Déterminer (par le calcul) les coordonnées (xG; yG) du point G vérifiant :
−→
GA + 2 −→ −→ −→
GB + GC = 0 .
( −→ 0 est le vecteur nul, c’est-à-dire le vecteur qui a pour coordonnées (0; 0)).
Placer G sur la figure.
L’égalité −→
GA + 2 −→ −→ −→
GB + GC = 0 se traduit par :
(1 − x) + 2(−1 − x) + (−2 − x) = 0
(−1 − y) + 2(−2 − y) + (2 − y) = 0
⎧
⎪⎨
−3 − 4x = 0 x = −
c’est-à-dire
, d’où
−3 − 4y = 0 ⎪⎩
3
4
y = − 3
4
Les coordonnées de G sont − 3
; −3
4 4
4. D’après la figure, que peut-on conjecturer pour les points B, G et D ?
Démontrer cette conjecture par le calcul.
On peut conjecturer que les points B, G, D sont alignés.
IV)
Démonstration :
−→ 1 5
BG ;
4 4
G
F
M
et −−→
BD (1; 5), donc −−→
BD = 4 −→
BG.
Les vecteurs −−→
BD et −→
BG sont colinéaires, donc les points B, G, D sont alignés.
C
B
O A
I
D
OABC est un carré de côté 4 cm.
E
M est le point défini par −→ −−→
OB = −2OM (DE) et (F G) sont les parallèles passant par M aux côtés (OA) et (OC) du carré.
On appelle I l’intersection des droites (MB) et (GD)
On se propose de démontrer que les droites (OB), (GD) et (F E) sont concourantes,
c’est-à-dire qu’elles passent par un même point (I).
On choisit un repère d’origine O et d’unité 1 cm, cde telle sorte que les coordonnées de
A soient (4; 0) et que celles de C soient (0; 4).
1. Déterminer les coordonnées des points B, G, F, D, E
Déterminer les coordonnées des vecteurs −→ −−→
OB et GD
B(4; 4), G(−2; 4); F (−2; 0); D(0; −2); E(4; −2)
−→
OB(4 − 0; 4 − 0) = (4; 4) −−→
GD(0 − (−2); −2 − 4) = (2; −6)
2. a) Pourquoi les vecteurs −→ OI et −→
OB sont-ils colinéaires ?
Les points O, B, M sont alignés parce que les vecteurs −−→
OM et −→
OB sont colinéaires,
puisque −→ −−→
OB = −2OM Or I est sur la droite (OM), donc les points O, I, B sont alignés.
Donc les vecteurs −→ OI et −→
OB sont colinéaires.
b) On note (x; y) les coordonnées du point I.
Traduire le fait que −→ OI et −→
OB sont colinéaires avec des coordonnées.
En déduire que y = x.
Lorsque deux vecteurs sont colinéaires, leurs coordonnées sont proportionnelles.
Or les coordonnées sont −→ OI(x; y) et −→
x y
OB(4; 4), donc = , donc x = y.
4 4
c) Démontrer que les coordonnées de −→
ID sont (−x; −2 − x).
Puisque les coordonnées de I sont (x; y), celles de −→
ID sont (0 − x; −2 − y). Or
x = y, donc les coordonnées de D sont (0 − x; −2 − x)
d) Pourquoi les vecteurs −→
ID et −−→
GD sont-ils colinéaires ?
En utilisant les coordonnées de −→
ID et −−→
GD, en déduire que x = − 1
2
Les points I, D et G sont alignés, donc les vecteurs −→
ID et −−→
GD sont colinéaires.
Les coordonnées sont −→
ID(0 − x; −2 − x) et −−→
GD(2; −6). Elles sont proportionnelles,
donc :
−x × (−6) = (−2 − x) × 2, d’où 6x = −4 − 2x, donc 8x = −4, donc x = − 1
2
3. Démontrer que les points F, I et E sont alignés en utilisant les vecteurs −→ F I et −→
F E
On calcule les coordonnées : −→
3 −→
F I ; −1 F E(6; −2).
2 2
Ces coordonnées sont proportionnelles : −→ −→ −→ −→
F E = 4F I, donc les vecteurs F I et F E
sont colinéaires.
Donc les points F, I, E sont alignés.