La fonction logarithme népérien

La fonction logarithme
népérien
I. Définition et propriétés algébriques
1. Définition
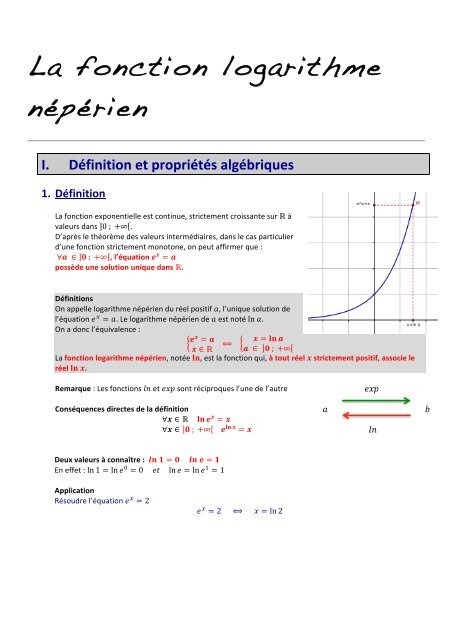
La fonction exponentielle est continue, strictement croissante sur ℝ à
valeurs dans 0 ; +∞ .
D’après le théorème des valeurs intermédiaires, dans le cas particulier
d’une fonction strictement monotone, on peut affirmer que :
∀! ∈ ! ; +∞ , l’équation ! ! = !
possède une solution unique dans ℝ.
Définitions
On appelle logarithme népérien du réel positif !, l’unique solution de
l’équation ! ! = !. Le logarithme népérien de ! est noté ln !.
On a donc l’équivalence :
! ! = !
! ∈ ℝ ⟺
! = !" !
! ∈ ! ; +∞
La fonction logarithme népérien, notée !", est la fonction qui, à tout réel ! strictement positif, associe le
réel !" !.
Remarque : Les fonctions !" et !"# sont réciproques l’une de l’autre
Conséquences directes de la définition
∀! ∈ ℝ !" ! ! = !
∀! ∈ ! ; +∞ ! !" ! = !
Deux valeurs à connaître : !" ! = ! !" ! = !
En effet : ln 1 = ln ! ! = 0 !" ln ! = ln ! ! = 1
Application
Résoudre l’équation ! ! = 2
! ! = 2 ⟺ ! = ln 2
!"#
! !
!"

2. Propriétés algébriques
Relation fonctionnelle
Pour tous réels ! et !, strictement positifs, !" !" = !" ! + !" !
Démonstration
! !" (!") = !"
! !" !!!" ! = ! !" ! ×! !" ! = !×!
On en déduit que ! !" (!") = ! !" !!!" ! ⟺ ln !" = ln ! + ln !
Remarque
Les seules fonctions vérifiant cette relation sont les fonctions du type ! ! = ! !" ! ! réel quelconque
Les propriétés qui découlent de cette relation
Pour tous réels ! et ! strictement positifs et tout entier relatif !,
!" !
! = −!" ! !" !
! = !" ! − !" ! !" !! = ! !" ! !" ! = !
! !" !
Démonstrations
• Pour la première formule, on transforme chaque membre de l’égalité en « passant à
l’exponentielle »
! !"!
! = 1
!
! ! !" ! = 1
! !" ! = 1
!
On en déduit donc que :
• Pour la deuxième formule :
ln a
b
! !"!
! = ! ! !" ! ⟺ !" !
! = −!" !
= ln !× 1
! = ln ! × ln 1
! = ln ! − ln !
• Pour la troisième formule : Démonstrations par récurrence
• Pour la quatrième formule :
!" ! = ln !× ! = ln ! + ln ! = ! !" !
On en déduit donc que : !" ! = !
! !" !
Applications
Exercice 1
Écrire les nombres !, !, ! en fonction de ln 2
! = ln 8 ! = ln 1
! = ln
4
2 ! = ln 6 − 2 + ln 6 + 2
! = ln 8 = ln 2 ! = 3 ln 2
! = ln 1
4 = − ln 4 = − ln 2! = −2 ln 2
! = ln 2 = 1
ln 2
2
! = ln 6 − 2 + ln 6 + 2 = ln ( 6 − 2)×( 6 + 2) = ln 6 − 4 = ln 2

Exercice 2
Écrire la fonction suivante à l’aide d’un seul logarithme après avoir déterminé l’ensemble de définition.
! ! = ln ! + 2 ln(! − 2)
! est définie si ! > 0 et ! − 2 > 0 ; ! est définie si ! > 2
Pour ! > ! : ! ! = ln ! + 2 ln(! − 2) = ln ! + ln ! − 2 ! = ln ! ! − 2 !
Remarque
Avant de simplifier une expression contenant des logarithmes il est très important de commencer par
déterminer l’ensemble de définition de cette expression.
II. Étude générale de la fonction logarithme
1. Sens de variation
Propriété (admise)
La fonction ln est continue sur son ensemble de définition 0 ; +∞ .
Remarque
On admet que la fonction réciproque d’une fonction continue est continue.
Propriété
La fonction !" est dérivable sur 0 ; +∞ et !! ! ! = !
Démonstration
! et ! sont deux réels strictement positifs distincts
On pose ln ! = ! !" ln ! = !. On a donc ! = ! ! !" ! = ! !
lim
!→!
ln ! − ln ! ! − !
= lim
! − ! !→! ! ! 1
= lim
− ! ! !→! ! ! − ! !
! − !
La fonction ln est dérivable en a et ln’ ! = !
Propriété
La fonction !" est strictement croissante sur 0 ; +∞
Démonstration
Sur 0 ; +∞ , ln′ ! = !
! > 0. On en déduit donc que la fonction ln est strictement croissante.
!
!
!" !"#$%%&'( !" !"#$ ! ! !""#$%&&'(')*+' !"#
= 1
! ! = 1
!
Propriété (qui se déduit de la stricte croissance de la fonction logarithme népérien)
! et ! deux réels strictement positifs quelconques
! = ! ⟺ !" ! = !! !
! < ! ⟺ !" ! < !" !
Signe de la fonction ln (à retenir)
!" ! > ! ⟺ ln ! > ln 1 ⟺ ! > !
!" ! < ! ⟺ ln ! < ln 1 ⟺ ! < !
! 0 !
!
+∞
ln ! − +

Application
Résoudre l’équation ln ! + 3 + ln ! − 2 = ln 6
Tout d’abord il faut déterminer l’ensemble de définition de cette équation.
Cette équation est définie si : ! + 3 > 0 et ! − 2 > 0
! > −3 et ! > 2 revient à dire ! > 2.
L’ensemble des solutions de l’équation est à chercher dans l’intervalle 2 ; +∞
ln ! + 3 ! − 2 = ln 6
ln ! + 3 + ln ! − 2 = ln 6 ⟺
! > 2
! + 3 ! − 2 = 6
⟺
! > 2
! + 3 ! − 2 = 6 ⟺ ! ! + ! − 12 = 0
∆= 1 + 48 = 49
−1 + 7
−1 − 7
! ! = = 3 ! ! = = −4 < !
2
2
L’équation ne possède donc qu’une solution : ! = 3
2. Limites en ! et en +∞
Théorème
!"# !" ! = −∞ !"# !" ! = +∞
!→! ! !→!!
Démonstration
Dire que la fonction ln tend vers +∞ si ! tend vers +∞ c’est dire que l’on peut rendre ln ! aussi grand que
l’on veut à partir du moment que l’on prenne un ! suffisamment grand.
∀A ∈ ℝ, ln ! > ! ⟺ ! > ! !
On a ainsi montré que : !"# !→!! !" ! = +∞
Pour la Limite en 0, on va effectué un changement de variable : on pose ! = !
Courbe représentative de la fonction
logarithme népérien
Remarque
lim ln ! = lim
!→! !
Les courbes représentatives de fonctions
réciproques sont symétriques par rapport à la
droite d’équation ! = !
!→!!
1
! = lim
− ln ! = −∞
!→!!
!

3. Une limite à connaître
Propriété
!"#
!→!
!"(! + !)
= !
!
Démonstration
ln 1 + ℎ − ln (1)
ℎ ≠ 0 ,
=
ℎ
ln 1 + ℎ
ℎ
On reconnaît la limite du taux de variation de la fonction ln en 1 ; elle est donc égale au nombre dérivé de la
fonction ln en 1.
ln ′(1) = 1
= 1
1
Remarque
On peut utiliser ce résultat de la façon suivante :
Si ℎ est « petit » ln 1 + ℎ ≈ ℎ
III. D’autres résultats
1. Dérivées et primitives avec la fonction !"
a. Dérivée de la fonction ! ⟼ !" (! ! )
Propriété
Si ! est une fonction dérivable et strictement positive sur un intervalle !, alors la fonction ln ! est dérivable
sur ! et
!" ! ! = ! ! × !
! = !!
!
Application
Calculer la dérivée de la fonction f définie sur 0 ; +∞ par ! ∶ ! ⟼ ln ! + 1
! est de la forme ln ! ave ! ! = ! + 1
! ! ! = ! ! ! × 1
! ! =
1
2 ! + 1
1
×
! + 1 =
1
2 ! + 1

. Primitives
Théorème : primitives de la fonction inverse
La fonction inverse admet des primitives sur 0 ; +∞ . Elles sont de la forme :
! ! ! = !" ! + ! ! ∈ ℝ
Démonstration
1 !
! ! ! =
!
Théorème : primitives de la fonction !!
!
Soit ! une fonction dérivable ne s’annulant pas sur un intervalle !.
Les primitives de la fonction !!
! sont de la forme !" ! + ! ! ∈ ℝ
Démonstration
Soit ! ! = ln !(!) + ! avec ! fonction dérivable sur !
Et ! ! = !! !
! !
1 er cas : ! > 0 sur !
! ! = ln ! ! + ! donc ! ! ! = !! !
! !
2 ème cas : ! < 0 sur !
= !(!)
! ! = ln −! ! + ! donc ! ! ! = − !! !
!! ! = !! !
! !
= ! !
On a bien montré que ! est la forme générale d’une primitive de ! sur !.
Conséquence
La fonction inverse admet également des primitives sur −∞ ; ! .
Elles sont de la forme ! ⟼ !" −! + ! ! ∈ ℝ
Application
Soit ! la fonction définie sur −1 ; 1 par :
! ! = !
! ! − 1
Déterminer la primitive ! ! de f qui s’annule en 0.
! ! = !
! ! − 1
1 2!
= ×
2 ! ! − 1
1 !′(!)
= ×
2 !(!)
! ! = ! ! − 1
Les primitives de ! sont de la forme : ! ⟼ !
! × ln ! ! + ! ! ∈ ℝ
Or sur −1 ; 1 ! ! < 0
On a donc :
! ! ! = 1
2 ln 1 − !! + !
⟺ ! ! ! =
! ! 0 = 0
1
2 ln(1 − !! )

2. Croissances comparées
Théorème
!" !
!"#
!→!! ! = ! !"#
! !" ! = !
!→! !
Remarques
Pour retrouver les résultats précédents, on peut retenir : « x l’emporte sur la fonction !" »
On pourrait également généraliser les résultats et montrer que :
!"#$ ! !"#$!! !"#$%&' !"! !"#, !"#
!→!!
3. La fonction logarithme décimal
Définition
La fonction logarithme décimal, noté log, définie sur 0 ; +∞ par :
!" !
!"# ! =
!" !"
Par définition, cette fonction a les mêmes propriétés que la fonction ln.
Propriété
Pour tout entier relatif !, !"# !" ! = !
Démonstration
log 10 ! =
ln 10!
ln 10
!" !
! ! = ! !"#
!→! ! !! !" ! = !
= ! ln 10
ln 10
= !