You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Introduction au filtrage<br />
numérique<br />
Signaux & Systèmes - M1 Physique -<br />
<strong>LPSC</strong>/UJF - F.Montanet<br />
Caractérisation des filtres linéaires<br />
Réponse impulsionnelle :<br />
Réponse indicielle :<br />
Réponse fréqu<strong>en</strong>tielle :<br />
j2<br />
ft<br />
e π<br />
Filtre<br />
Filtre<br />
Filtre<br />
3<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Introduction<br />
Le filtrage a deux applications principales :<br />
1. séparation de signaux combinés (démultiplexage).<br />
2. restoration de signaux distordus<br />
Les filtres analogiques électroniques sont utilisés pour les<br />
mêmes taches, néanmoins, les filtres numériques atteign<strong>en</strong>t<br />
des performances bi<strong>en</strong> supérieures.<br />
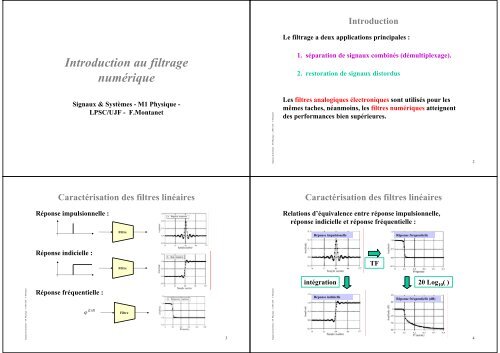
Caractérisation des filtres linéaires<br />
Relations d’équival<strong>en</strong>ce <strong>en</strong>tre réponse impulsionnelle,<br />
réponse indicielle et réponse fréqu<strong>en</strong>tielle :<br />
Réponse impulsionelle Réponse fréqu<strong>en</strong>tielle<br />
Réponse indicielle<br />
TF<br />
intégration 20 Log 10( )<br />
Réponse fréqu<strong>en</strong>tielle (dB)<br />
2<br />
4
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
<strong>Transformation</strong> <strong>en</strong> z<br />
Cours signaux et systèmes<br />
M1 physique<br />
<strong>Transformation</strong> <strong>en</strong> Z<br />
La transformation <strong>en</strong> z repr<strong>en</strong>d le formalisme et les propriétés de la<br />
transformation de Laplace et les applique aux signaux discrets.<br />
Transformée <strong>en</strong> Z = Transformée de Laplace<br />
de la fonction échantillonnée avec z = e Ts ou T est la période d’échantillonnage.<br />
<strong>Transformation</strong> de Laplace <strong>Transformation</strong> <strong>en</strong> Z<br />
Exemple :<br />
e(t)<br />
1<br />
1/2<br />
t<br />
10<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Relations <strong>en</strong>tre Laplace et TZ<br />
Transformée de Laplace de x[kT], signal échantillonné :<br />
Définition<br />
Quelques propriétés<br />
Linéarité<br />
Décalage temporel :<br />
Convolution :<br />
Multiplication par série<br />
expon<strong>en</strong>tielle :<br />
Transformée <strong>en</strong> Z<br />
Somme de série... donc problèmes de converg<strong>en</strong>ce !<br />
9<br />
11
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Propriétés de la transformées <strong>en</strong> Z<br />
Retard :<br />
Cette propriété est particulièrem<strong>en</strong>t importante. Elle donne<br />
tout son intérêt à la TZ. En effet, la multiplication par z -1<br />
correspond à la translation <strong>en</strong> temps d'un échantillon au<br />
suivant :<br />
Avance :<br />
Échelon unitaire :<br />
Rampe unitaire :<br />
à démontrer<br />
Transformées <strong>en</strong> Z<br />
conditions initiales<br />
12<br />
14<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Propriétés de la transformées <strong>en</strong> Z<br />
Conditions initiales et finales :<br />
Convolution :<br />
Expon<strong>en</strong>tielle :<br />
Sinus et Cosinus :<br />
Transformées <strong>en</strong> Z<br />
si ces limites exist<strong>en</strong>t<br />
13<br />
15
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Systèmes différ<strong>en</strong>tiels et TZ<br />
x[n]<br />
Système<br />
y[n]<br />
La sortie y[n] et x[n] d’un système physique linéaire<br />
échantillonné sont reliés par une équation aux différ<strong>en</strong>ces :<br />
y( n)<br />
+ a1y(<br />
n −1)<br />
+ ... + a My(<br />
n − M)<br />
= b0x(<br />
n)<br />
+ b1x(<br />
n −1)<br />
+ ... + b Nx(<br />
n − N)<br />
Causal : N ≥ M<br />
la sortie au temps nT dép<strong>en</strong>d des valeurs des échantillons connu à ce mom<strong>en</strong>t<br />
c.a.d x[n], x[n-1], x[n-2]… et y[n-1], y[n-2], … et des caractéristiques du<br />
systèmes définies par les a k et b k (système linéaire causal)<br />
Fonction de transfert et Pôles<br />
dans le domaine Z<br />
Fonction de transfert <strong>en</strong> z, un rapport de polynômes <strong>en</strong> z avec M ≤<br />
N pour un système physique.<br />
qui peut se mettre égalem<strong>en</strong>t sous la forme :<br />
Les zi sont les zéros et les pj sont les pôles du système.<br />
Les zéros et les pôles décriv<strong>en</strong>t le système à un facteur d’amplitude près a0 (gain statique) et à un retard près z N - M avec N - M ≤ 0.<br />
En particulier, on appellera :<br />
• filtres MA (à Moy<strong>en</strong>ne Adaptée) les filtres n’ayant que des zéros<br />
(et des pôles <strong>en</strong> z = 0)<br />
• filtres AR (Auto Régressifs) les filtres n’ayant que des pôles<br />
(et des zéros <strong>en</strong> z =0)<br />
!<br />
16<br />
18<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Fonction de transfert et Pôles<br />
dans le domaine Z<br />
En pr<strong>en</strong>ant la TZ et <strong>en</strong> utilisant les propriétés de linéarité et de<br />
translation <strong>en</strong> temps, on obti<strong>en</strong>t :<br />
Donc :<br />
Y( z) = H( z) X ( z)<br />
Pôles dans le domaine Z<br />
17<br />
19
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
On retrouve la transformée<br />
de Fourier discrète du<br />
signal x[k], et sa périodicité<br />
2πF e =2π/T<br />
0<br />
Relations <strong>en</strong>tre TZ et Fourier<br />
Im(s)=ω<br />
Re(s)=r<br />
6πFe<br />
4πFe<br />
2πFe<br />
0<br />
-2πFe<br />
-4πFe<br />
-6πFe<br />
f = 1/2<br />
Im(s)<br />
Plan de Laplace<br />
Plan de Laplace Plan des Z<br />
0<br />
Im(z)<br />
f = 1/4<br />
1<br />
-1<br />
Re(s)<br />
f=0<br />
f=1<br />
Re(z)<br />
Im(z)<br />
1<br />
Plan des Z<br />
f croissante<br />
Im(z)<br />
1<br />
f = 0<br />
Re(z)<br />
f = 1<br />
f=0<br />
f=1<br />
Re(z)<br />
20<br />
22<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
-a<br />
Le plan ou domaine z<br />
Interprétation géométrique de la TZ<br />
ρ<br />
0<br />
Plan Z<br />
ϕ<br />
1<br />
Re(z)<br />
f = 0<br />
f = 1<br />
Périodicité de X( f )<br />
21<br />
23
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Caractérisation des filtres linéaires<br />
Implém<strong>en</strong>tation par convolution :<br />
Filtres à Réponse Impulsionnelle Finie<br />
RIF (ou FIR <strong>en</strong> anglais)<br />
Implém<strong>en</strong>tation par récurr<strong>en</strong>ce :<br />
Filtres à Réponse Impulsionnelle Infinie<br />
RII (ou IIR <strong>en</strong> anglais)<br />
Caractérisation dans le domaine fréqu<strong>en</strong>tiel<br />
Bande passante, bande atténuée, passe-haut, passe-bas,<br />
passe-bande, coupe-bande.<br />
Amplitudes<br />
Amplitudes<br />
bande<br />
passante<br />
Passe-bas<br />
bande de<br />
transition<br />
Passe-bande<br />
bande<br />
atténuée<br />
Fréqu<strong>en</strong>ces<br />
Fréqu<strong>en</strong>ces<br />
Amplitudes<br />
Amplitudes<br />
Passe-haut<br />
Coupe-bande<br />
Fréqu<strong>en</strong>ces<br />
Fréqu<strong>en</strong>ces<br />
24<br />
27<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Caractérisation des filtres linéaires<br />
Implém<strong>en</strong>tation d’un filtre numérique par récurr<strong>en</strong>ce :<br />
La sortie y[n] est calculée par combinaison linéaire<br />
des x[n], x[n-1], x[n-2]…<br />
et des y[n-1], y[n-2], …<br />
par une équation de récurr<strong>en</strong>ce<br />
et des coeffici<strong>en</strong>ts de récurr<strong>en</strong>ce:<br />
y[<br />
n]<br />
= a<br />
0<br />
x[<br />
n]<br />
+ a x[<br />
n<br />
1<br />
−1]<br />
+ a<br />
x[<br />
n<br />
− 2]<br />
+ a<br />
x[<br />
n<br />
− 3]<br />
+ …<br />
+ b y[<br />
n −1]<br />
+ b y[<br />
n − 2]<br />
+ b y[<br />
n − 3]<br />
+ …<br />
1<br />
Inversion spectrale<br />
2<br />
2<br />
3<br />
3<br />
25<br />
29
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Symétrie spectrale<br />
Changem<strong>en</strong>t de signe d’un échantillon sur deux<br />
⇒ multiplication par e j2πk/2<br />
⇒ convolution du spectre<br />
par δ(f-0.5)<br />
⇒ décalage du spectre<br />
de 0.5<br />
⇒ la partie négative<br />
du spectre<br />
pr<strong>en</strong>d la place<br />
de la partie positive.<br />
Classification des filtres<br />
Les filtres sont classifié selon leur fonction ou selon leur implém<strong>en</strong>tation:<br />
Fonction<br />
Domaine temporel<br />
(lissage, suppression<br />
de niveau continu)<br />
Domaine Fréqu<strong>en</strong>tiel<br />
(séparation de<br />
fréqu<strong>en</strong>ce)<br />
Spécifique<br />
(Déconvolution)<br />
Implém<strong>en</strong>tation<br />
Moy<strong>en</strong>ne mobile Pôle unique<br />
F<strong>en</strong>êtres Tchebycheff<br />
RIF sur mesure Récursif<br />
30<br />
32<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Construction<br />
d’un passe-bande ou d’un coupe-bande<br />
Par convolution, RIF Par récursivité, RII Filtres Récursifs<br />
31
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
x[n]<br />
Filtre<br />
RIF<br />
y[<br />
n]<br />
y[<br />
n]<br />
H[<br />
z]<br />
x[n]<br />
Fonction de transfert<br />
par la transformation <strong>en</strong> Z<br />
x[n-1] x[n-2]<br />
z -1 z -1 z -1<br />
a 0 a 1 a 2 a 3<br />
y[<br />
n]<br />
H[<br />
z]<br />
=<br />
x[n-3]<br />
Σ Σ Σ<br />
−1<br />
−2<br />
−3<br />
( a + a z + a z + a z )<br />
0<br />
1<br />
y[<br />
n]<br />
= = a<br />
x[<br />
n]<br />
0<br />
2<br />
+ a z<br />
−1<br />
1<br />
+ a<br />
2<br />
3<br />
z<br />
−2<br />
x[<br />
n]<br />
+ a<br />
Fonction de transfert<br />
par la transformation <strong>en</strong> Z<br />
z -1 z -1 z -1<br />
3<br />
z<br />
−3<br />
Filtre récursif RII d’ordre 1<br />
combinaison d’un RIF et d’un<br />
RII simple<br />
−1<br />
−2<br />
−3<br />
−1<br />
−2<br />
−3<br />
= ( a 0 + a1z<br />
+ a 2z<br />
+ a 3z<br />
) x[<br />
n]<br />
+ ( b1z<br />
+ b2z<br />
+ b3z<br />
)<br />
−1<br />
−2<br />
−3<br />
−1<br />
−2<br />
−3<br />
( 1−<br />
b z − b z − b z ) = ( a + a z + a z + a z ) x<br />
1<br />
x[n-1] x[n-2]<br />
a 0 a 1 a 2 a 3<br />
Σ Σ Σ<br />
2<br />
y[<br />
n]<br />
a 0 + a z + a z +<br />
= =<br />
x[<br />
n]<br />
1−<br />
b − b −<br />
−1<br />
1<br />
−1<br />
1z<br />
3<br />
x[n-3]<br />
−2<br />
2<br />
−2<br />
2z<br />
Σ Σ Σ<br />
b 3 b 2 b 1<br />
z -1<br />
0 1<br />
−3<br />
a 3z<br />
−3<br />
b3z<br />
2<br />
z -1<br />
3<br />
z -1<br />
[ n]<br />
y[n]<br />
y[n]<br />
y[<br />
n]<br />
34<br />
36<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Filtre<br />
récursif<br />
RII simple<br />
x[n]<br />
Fonction de transfert<br />
par la transformation <strong>en</strong> Z<br />
y[<br />
n]<br />
y[<br />
n]<br />
Σ Σ Σ<br />
b 3 b 2 b 1<br />
H[<br />
z]<br />
z -1<br />
z -1<br />
−1<br />
−2<br />
−3<br />
= x[<br />
n]<br />
+ ( b1z<br />
+ b2z<br />
+ b3z<br />
)<br />
−1<br />
−2<br />
−3<br />
( 1−<br />
b z − b z − b z ) = x<br />
1<br />
y[<br />
n]<br />
= =<br />
x[<br />
n]<br />
1−<br />
b z<br />
2<br />
1<br />
−1<br />
3<br />
1<br />
− b z<br />
2<br />
−2<br />
[ n]<br />
− b<br />
Fonction de transfert<br />
par la transformation <strong>en</strong> Z<br />
3<br />
y[<br />
n]<br />
Filtre récursif combinaison RIF et RII du second ordre.<br />
x[n]<br />
Σ Σ<br />
z -1<br />
z -1<br />
x[n-2]<br />
x[n-1]<br />
a 0<br />
a 1<br />
a 2<br />
y[<br />
n]<br />
= b1y[<br />
n −1]<br />
+ b2y[<br />
n − 2]<br />
+ a x[<br />
n]<br />
+ a1x[<br />
n −1]<br />
+ a 2x[<br />
n − 2]<br />
y[<br />
n]<br />
a 0 + a z + a<br />
H[<br />
z]<br />
= =<br />
x[<br />
n]<br />
1−<br />
b − b<br />
−1<br />
1<br />
−1<br />
1z<br />
Σ<br />
0<br />
−2<br />
2z<br />
−2<br />
2z<br />
Σ<br />
b 1<br />
b 2<br />
z<br />
z -1<br />
z -1<br />
−3<br />
y[n-2]<br />
y[n-1]<br />
z -1<br />
y[n]<br />
y[n]<br />
35<br />
37
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
x[n]<br />
x[n]<br />
Filtre récursif combinaison<br />
RIF et RII du second ordre<br />
z -1<br />
z -1<br />
x[n-2]<br />
x[n-1]<br />
a 0<br />
a 1<br />
a 2<br />
Σ<br />
Σ<br />
Filtre récursif combinaison<br />
RIF et RII du second ordre<br />
Σ Σ<br />
Σ<br />
b 1<br />
b 2<br />
w[n]<br />
z -1<br />
z -1<br />
w[n-2]<br />
Σ<br />
Σ<br />
w[n-1]<br />
a 0<br />
a 1<br />
a 2<br />
b 1<br />
b 2<br />
Σ<br />
z -1<br />
z -1<br />
y[n-2]<br />
y[n-1]<br />
y[n]<br />
y[n]<br />
38<br />
40<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
y[<br />
n]<br />
w[<br />
n]<br />
H[<br />
z]<br />
=<br />
=<br />
=<br />
x[n]<br />
Σ<br />
Σ<br />
Filtre récursif combinaison<br />
RIF et RII du second ordre<br />
b 1<br />
b 2<br />
z -1<br />
z -1<br />
w[n-2]<br />
w[n-1]<br />
z -1<br />
z -1<br />
w[n-2]<br />
w[n-1]<br />
Fonction de transfert<br />
par la transformation <strong>en</strong> Z<br />
Filtre récursif combinaison RIF et RII du second ordre.<br />
−1<br />
−2<br />
( a 0 + a1z<br />
+ a 2z<br />
) w<br />
−1<br />
−2<br />
x[<br />
n]<br />
+ ( b z + b z )<br />
y[<br />
n]<br />
x[<br />
n]<br />
1<br />
x[n]<br />
a 0 + a z + a z<br />
=<br />
1−<br />
b − b<br />
2<br />
−1<br />
1<br />
−1<br />
1z<br />
[ n]<br />
w[<br />
n]<br />
−2<br />
2<br />
−2<br />
2z<br />
Σ Σ<br />
Σ<br />
b 1<br />
b 2<br />
w[n]<br />
z -1<br />
z -1<br />
w[n-2]<br />
a 0<br />
a 1<br />
a 2<br />
w[n-1]<br />
a 0<br />
a 1<br />
a 2<br />
Σ<br />
Σ<br />
Σ<br />
y[n]<br />
39<br />
y[n]<br />
41
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
x[n]<br />
Fonction de transfert<br />
par la transformation <strong>en</strong> Z<br />
Filtre récursif d’ordre 4 utilisant <strong>en</strong> cascade deux combinaisons<br />
RIF et RII du second ordre.<br />
Σ Σ<br />
Σ<br />
b 1<br />
b 2<br />
z -1<br />
z -1<br />
a 0<br />
a 1<br />
a 2<br />
Σ<br />
Σ Σ<br />
Σ<br />
b 1<br />
b 2<br />
z -1<br />
z -1<br />
1 2<br />
y[<br />
n]<br />
a 0 a1z<br />
a 2z<br />
H[ z]<br />
1 2<br />
x[<br />
n]<br />
1 b1z<br />
b2z<br />
⎟ − −<br />
⎛ + + ⎞<br />
= = ⎜<br />
− −<br />
⎝ − − ⎠<br />
Filtres à Moy<strong>en</strong>ne Mobile<br />
(RIF)<br />
Signaux & Systèmes - M1 Physique -<br />
<strong>LPSC</strong>/UJF - F.Montanet<br />
2<br />
a 0<br />
a 1<br />
a 2<br />
Σ<br />
y[n]<br />
42<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Filtre récursif combinaison<br />
RIF et RII du second ordre<br />
Forme dite canonique directe:<br />
b10 b20 bn0<br />
Filtres à Moy<strong>en</strong>ne Mobile<br />
Le filtrage à moy<strong>en</strong>ne mobile est d’usage courrant<br />
et il est simple à concevoir et à utiliser.<br />
C’est un filtre bi<strong>en</strong> adapté à la réduction de bruit<br />
de signaux <strong>en</strong>codé <strong>en</strong> temps.<br />
Il est <strong>en</strong> revanche très peu efficace dans le domaine<br />
fréqu<strong>en</strong>tiel notamm<strong>en</strong>t pour la séparation de fréqu<strong>en</strong>ce.<br />
Il existe des variantes de ce type de filtre plus performantes<br />
dans le domaine fréqu<strong>en</strong>tiel, tels que les filtres à moy<strong>en</strong>ne<br />
mobile Gaussi<strong>en</strong>s, de Blackman et à passes multiples.<br />
43<br />
45
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Implém<strong>en</strong>tation par convolution<br />
Calcul de la moy<strong>en</strong>ne mobile :<br />
Variante symétrique / k :<br />
Noyau pour la convolution<br />
(par exemple sur 5 points):<br />
y[<br />
k]<br />
=<br />
1<br />
M<br />
∑ − M 1<br />
i=<br />
0<br />
1<br />
y[<br />
k]<br />
=<br />
2M<br />
+ 1<br />
x[<br />
k + i]<br />
M<br />
∑<br />
i=<br />
−M<br />
x[<br />
k + i]<br />
… , 0,<br />
0,<br />
1 , 1 , 1 , 1 , 1 , 0,<br />
0,<br />
…<br />
5 5 5 5 5<br />
100 'MOVING AVERAGE FILTER<br />
110 'This program filters 5000 samples with a 101 point moving<br />
120 'average filter, resulting in 4900 samples of filtered data.<br />
130 '<br />
140 DIM X[4999] 'X[ ] holds the input signal<br />
150 DIM Y[4999] 'Y[ ] holds the output signal<br />
160 '<br />
170 GOSUB XXXX 'Mythical subroutine to load X[ ]<br />
180 '<br />
190 FOR I% = 50 TO 4949 'Loop for each point in the output signal<br />
200 Y[I%] = 0 'Zero, so it can be used as an accumulator<br />
210 FOR J% = -50 TO 50 'Calculate the summation<br />
220 Y[I%] = Y[I%] + X(I%+J%]<br />
230 NEXT J%<br />
240 Y[I%] = Y[I%]/101 'Complete the average by dividing<br />
250 NEXT I%<br />
260 '<br />
270 END<br />
Réponse <strong>en</strong> fréqu<strong>en</strong>ce<br />
Le noyau du filtre à moy<strong>en</strong>ne mobile est une fonction créneau.<br />
Sa TF est une fonction sinc :<br />
H[<br />
f ]<br />
sin[ πfM]<br />
=<br />
M sin[ πf<br />
]<br />
46<br />
48<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Filtrage de bruit blanc<br />
On peut montrer que le filtrage à moy<strong>en</strong>ne mobile est la méthode optimale parmi<br />
tout les filtres linéaires pour la réduction de bruit tout <strong>en</strong> préservant au mieux<br />
les sauts du signal.<br />
11 points<br />
51 points<br />
Filtre à moy<strong>en</strong>ne mobile multi-passes.<br />
47<br />
49
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Filtre à moy<strong>en</strong>ne mobile à f<strong>en</strong>être<br />
Gaussi<strong>en</strong>ne ou de Blackman<br />
Filtres à F<strong>en</strong>êtres<br />
Cours DSP<br />
50<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Implém<strong>en</strong>tation par récursivité<br />
Calcul de la moy<strong>en</strong>ne mobile par récursion :<br />
y[<br />
i]<br />
= y[<br />
i −1]<br />
+ x[<br />
i + M]<br />
− x[<br />
i − M −1]<br />
100 'MOVING AVERAGE FILTER IMPLEMENTED BY RECURSION<br />
110 'This program filters 5000 samples with a 101 point moving<br />
120 'average filter, resulting in 4900 samples of filtered data.<br />
130 'A double precision accumulator is used to prev<strong>en</strong>t round-off drift.<br />
140 '<br />
150 DIM X[4999] 'X[ ] holds the input signal<br />
160 DIM Y[4999] 'Y[ ] holds the output signal<br />
170 DEFDBL ACC 'Define the variable ACC to be double precision<br />
180 '<br />
190 GOSUB XXXX 'Mythical subroutine to load X[ ]<br />
200 '<br />
210 ACC = 0 'Find Y[50] by averaging points X[0] to X[100]<br />
220 FOR I% = 0 TO 100<br />
230 ACC = ACC + X[I%]<br />
240 NEXT I%<br />
250 Y[50] = ACC/101<br />
260 ' 'Recursive moving average filter<br />
270 FOR I% = 51 TO 4949<br />
280 ACC = ACC + X[I%+50] - X[I%-51]<br />
290 Y[I%] = ACC/101<br />
300 NEXT I%<br />
310 '<br />
320 END<br />
Nota b<strong>en</strong>e: bi<strong>en</strong> que cette implém<strong>en</strong>tation soit récursive, ce filtre est à réponse<br />
impulsionnelle finie RIF<br />
Filtres à F<strong>en</strong>être<br />
Les filtres à f<strong>en</strong>être (compr<strong>en</strong>dre f<strong>en</strong>être fréqu<strong>en</strong>tielle)<br />
sont utilisés pour séparer différ<strong>en</strong>tes fréqu<strong>en</strong>ces.<br />
Ils peuv<strong>en</strong>t atteindre des niveaux de performances<br />
extrêmem<strong>en</strong>t poussés dans le domaine fréqu<strong>en</strong>tiel.<br />
Ils sont <strong>en</strong> revanche mal adaptés pour conserver la forme des<br />
signaux dans le domaine temporel, avec des effets<br />
d’overshoot et d’oscillation assez désastreux.<br />
Ils peuv<strong>en</strong>t être facilem<strong>en</strong>t implém<strong>en</strong>tés par le calcul de la<br />
convolution, mais cette méthode est coûteuse <strong>en</strong> temps de<br />
calcul. Il est <strong>en</strong> revanche possible de les réaliser très<br />
efficacem<strong>en</strong>t <strong>en</strong> utilisant la FFT.<br />
51<br />
53
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Noyau de filtre<br />
idéal,<br />
f<strong>en</strong>être<br />
spectrale ou<br />
fonction sinc.<br />
Noyau de filtre<br />
tronqué<br />
On rajoute un<br />
filtre avec f<strong>en</strong>être<br />
de Hamming ou<br />
Blackman<br />
Noyau de filtre<br />
adouci et r<strong>en</strong>du<br />
fini par la f<strong>en</strong>être<br />
Hanning:<br />
Bartlett:<br />
Stratégie des filtres à f<strong>en</strong>être<br />
Autres f<strong>en</strong>êtres<br />
Ondulations,<br />
conséqu<strong>en</strong>ce de<br />
la troncature<br />
⎧0. 5 + 0.<br />
5cos(<br />
2πk<br />
/ M)<br />
pour k ≤ M / 2<br />
w[<br />
k]<br />
= ⎨<br />
⎩0<br />
ailleurs<br />
⎧2k<br />
/ M pour - M/2 ≤ k < 0<br />
⎪<br />
w[ k]<br />
= ⎨1<br />
− 2k<br />
/ M pour 0 ≤ k ≤ M / 2 ( fonction triangle)<br />
⎪<br />
⎩0<br />
ailleurs<br />
Ondulations<br />
atténuées mais<br />
zone de transition<br />
élargie<br />
Hamming : atténuation 20% plus rapide que Blackman mais atténuation plus faible.<br />
Atténuation Largeur de transition Ondulations<br />
(/Hamming) de bande passante<br />
Blackman -74dB 0.02% 0.80 0.02%<br />
Hamming -53dB 0.2% 1 (ref) 0.2%<br />
Hanning -44dB 0.63% ~1<br />
Barlett -25dB 5.6% ~1<br />
Rectangle (ou sans f<strong>en</strong>être) -21dB 8.9% 0.25<br />
54<br />
56<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Hamming:<br />
Blackman:<br />
F<strong>en</strong>être de Hamming et de Blackman<br />
( 1−<br />
α)<br />
⎧α + cos( 2πk<br />
/ M)<br />
pour k ≤ M / 2<br />
w[<br />
k]<br />
= ⎨<br />
⎩0<br />
ailleurs<br />
avec α = 0.54<br />
⎧α + ( 1−<br />
α + β)<br />
cos( 2πk<br />
/ M)<br />
− βcos(<br />
4πk<br />
/ M)<br />
pour k ≤ M / 2<br />
w[<br />
k]<br />
= ⎨<br />
⎩0<br />
ailleurs<br />
Synthèse de filtre à f<strong>en</strong>être<br />
La formule complète pour le noyau d’un filtre f<strong>en</strong>être de Blackman<br />
sin(<br />
2πfC<br />
( k − M / 2)<br />
) ⎛<br />
⎛ 2πk<br />
⎞ ⎛ 4πk<br />
⎞⎞<br />
h[ i]<br />
= K<br />
⎜0.<br />
42 − 0.<br />
5cos⎜<br />
⎟ + 0.<br />
08cos⎜<br />
⎟⎟<br />
k − M / 2 ⎝<br />
⎝ M ⎠ ⎝ M ⎠⎠<br />
55<br />
57
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Implém<strong>en</strong>tation d’un<br />
filtre f<strong>en</strong>être de<br />
Hamming, filtrant 5000<br />
points avec un noyau de<br />
101 points de longueur<br />
(M=100) et produisant<br />
4900 échantillons filtrés.<br />
Hautes performances !<br />
Synthèse de filtre à f<strong>en</strong>être<br />
100 'LOW-PASS WINDOWED-SINC FILTER<br />
110 'This program filters 5000 samples with a 101 point windowed-sinc filter,<br />
120 'resulting in 4900 samples of filtered data.<br />
130 '<br />
140 DIM X[4999] 'X[ ] holds the input signal<br />
150 DIM Y[4999] 'Y[ ] holds the output signal<br />
160 DIM H[100] 'H[ ] holds the filter kernel<br />
170 '<br />
180 PI = 3.14159265<br />
190 FC = .14 'Set the cutoff frequ<strong>en</strong>cy (betwe<strong>en</strong> 0 and 0.5)<br />
200 M% = 100 'Set filter l<strong>en</strong>gth (101 points)<br />
210 '<br />
220 GOSUB XXXX 'Mythical subroutine to load X[ ]<br />
230 '<br />
240 ' 'Calculate the low-pass filter kernel<br />
250 FOR I% = 0 TO 100<br />
260 IF (I%-M%/2) = 0 THEN H[I%] = 2*PI*FC<br />
270 IF (I%-M%/2) 0 THEN H[I%] = SIN(2*PI*FC * (I%-M%/2)) / (I%-M%/2)<br />
280 H[I%] = H[I%] * (0.54 - 0.46*COS(2*PI*I%/M%) )<br />
290 NEXT I%<br />
300 '<br />
310 SUM = 0 'Normalize the low-pass filter kernel for<br />
320 FOR I% = 0 TO 100 'unity gain at DC<br />
330 SUM = SUM + H[I%]<br />
340 NEXT I%<br />
350 '<br />
360 FOR I% = 0 TO 100<br />
370 H[I%] = H[I%] / SUM<br />
380 NEXT I%<br />
390 '<br />
400 FOR J% = 100 TO 4999 'Convolve the input signal & filter kernel<br />
410 Y[J%] = 0<br />
420 FOR I% = 0 TO 100<br />
430 Y[J%] = Y[J%] + X[J%-I%] * H[I%]<br />
440 NEXT I%<br />
450 NEXT J%<br />
460 '<br />
470 END<br />
Synthèse de filtre à f<strong>en</strong>être<br />
Obt<strong>en</strong>u <strong>en</strong> convoluant un filtre f<strong>en</strong>être par lui même.<br />
58<br />
60<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Synthèse de filtre à f<strong>en</strong>être<br />
Implém<strong>en</strong>tation d’un filtre f<strong>en</strong>être passe-bande.<br />
100 'BAND-PASS WINDOWED-SINC FILTER<br />
110 'This program calculates an 801 point band-pass filter kernel<br />
120 '<br />
130 DIM A[800] 'A[ ] workspace for the lower cutoff<br />
140 DIM B[800] 'B[ ] workspace for the upper cutoff<br />
150 DIM H[800] 'H[ ] holds the final filter kernel<br />
160 '<br />
170 PI = 3.1415926<br />
180 M% = 800 'Set filter kernel l<strong>en</strong>gth (801 points)<br />
190 '<br />
200 ' 'Calculate the first low-pass filter kernel via Eq. 16-4,<br />
210 FC = 0.196 'with a cutoff frequ<strong>en</strong>cy of 0.196, store in A[ ]<br />
220 FOR I% = 0 TO 800<br />
230 IF (I%-M%/2) = 0 THEN A[I%] = 2*PI*FC<br />
240 IF (I%-M%/2) 0 THEN A[I%] = SIN(2*PI*FC * (I%-M%/2)) / (I%-M%/2)<br />
250 A[I%] = A[I%] * (0.42 - 0.5*COS(2*PI*I%/M%) + 0.08*COS(4*PI*I%/M%))<br />
260 NEXT I%<br />
270 '<br />
280 SUM = 0 'Normalize the first low-pass filter kernel for<br />
290 FOR I% = 0 TO 800 'unity gain at DC<br />
300 SUM = SUM + A[I%]<br />
310 NEXT I%<br />
320 '<br />
330 FOR I% = 0 TO 800<br />
340 A[I%] = A[I%] / SUM<br />
350 NEXT I%<br />
360 ' 'Calculate the second low-pass filter kernel via Eq. 16-4,<br />
370 FC = 0.204 'with a cutoff frequ<strong>en</strong>cy of 0.204, store in B[ ]<br />
380 FOR I% = 0 TO 800<br />
390 IF (I%-M%/2) = 0 THEN B[I%] = 2*PI*FC<br />
400 IF (I%-M%/2) 0 THEN B[I%] = SIN(2*PI*FC * (I%-M%/2)) / (I%-M%/2)<br />
410 B[I%] = B[I%] * (0.42 - 0.5*COS(2*PI*I%/M%) + 0.08*COS(4*PI*I%/M%))<br />
420 NEXT I%<br />
430 '<br />
440 SUM = 0 'Normalize the second low-pass filter kernel for<br />
450 FOR I% = 0 TO 800 'unity gain at DC<br />
460 SUM = SUM + B[I%]<br />
470 NEXT I%<br />
480 '<br />
490 FOR I% = 0 TO 800<br />
500 B[I%] = B[I%] / SUM<br />
510 NEXT I%<br />
520 '<br />
530 FOR I% = 0 TO 800 'Change the low-pass filter kernel in B[ ] into a high-pass<br />
540 B[I%] = - B[I%] 'filter kernel using spectral inversion (as in Fig. 14-5)<br />
550 NEXT I%<br />
560 B[400] = B[400] + 1<br />
570 '<br />
580 '<br />
590 FOR I% = 0 TO 800 'Add the low-pass filter kernel in A[ ], to the high-pass<br />
600 H[I%] = A[I%] + B[I%] 'filter kernel in B[ ], to form a band-reject filter kernel<br />
610 NEXT I% 'stored in H[ ] (as in Fig. 14-8)<br />
620 '<br />
630 FOR I% = 0 TO 800 'Change the band-reject filter kernel into a band-pass<br />
640 H[I%] = -H[I%] 'filter kernel by using spectral inversion<br />
650 NEXT I%<br />
660 H[400] = H[400] + 1<br />
670 ' 'The band-pass filter kernel now resides in H[ ]<br />
680 END<br />
Filtres à réponse arbitraire<br />
Cours signaux et systèmes<br />
M1 physique<br />
2004-2005<br />
F. Montanet UJF<br />
59
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Filtres à F<strong>en</strong>être<br />
Les filtres classiques sont passe-haut, passe-bas, passe-bande,<br />
coupe-bande. Il est possible de construire des filtres<br />
numériques ayant une réponse fréqu<strong>en</strong>tielle<br />
arbitrairem<strong>en</strong>t choisie.<br />
C’est un des domaines d’application ou les techniques DSP<br />
excell<strong>en</strong>t.<br />
Les applications typiques de ce g<strong>en</strong>re de filtre sont:<br />
la déconvolution, permettant de restaurer un signal<br />
ayant subit des distorsions de spectre connu,<br />
le filtrage optimal utilisé dans la séparation de signaux<br />
dont les spectres fréqu<strong>en</strong>tielles se recouvr<strong>en</strong>t.<br />
Effet de la longueur du noyau<br />
M = 10 M = 30<br />
M = 100 M = 300 M = 1000<br />
62<br />
64<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Réponse<br />
impulsionnelle<br />
obt<strong>en</strong>ue par TFD<br />
inverse (avec<br />
repliem<strong>en</strong>t)<br />
Noyau du filtre<br />
obt<strong>en</strong>ue par<br />
troncature à M,<br />
décalage de M/2<br />
et multiplication<br />
par une f<strong>en</strong>être<br />
de Hamming.<br />
Stratégie du filtrage à réponse arbitraire<br />
Domaine Temporel Domaine Fréqu<strong>en</strong>tiel<br />
Troncature,<br />
décalage,<br />
f<strong>en</strong>êtrage<br />
TFD -1<br />
Exemple d’un signal à déconvoluer<br />
Réponse<br />
fréqu<strong>en</strong>tielle<br />
souhaitée.<br />
Réponse<br />
fréqu<strong>en</strong>tielle<br />
réalisée.<br />
Détection de rayons gamma par un scintillateur.<br />
Le dépôt d’énergie est quasi instantané, mais l’émission de lumière de<br />
scintillation par le cristal suit une loi de décroissance expon<strong>en</strong>tielle. Le photodétecteur<br />
(photomultiplicateur) et l’électronique associée ont aussi une<br />
fonction de transfert qui n’est pas neutre. Le signal résultant de l’interaction<br />
d’un gamma à une forme bi<strong>en</strong> caractéristique qui est la réponse impulsionelle<br />
du système.<br />
63<br />
65
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Exemple d’un signal à déconvoluer<br />
Détection de rayons gamma par un scintillateur.<br />
Signal détecté<br />
correspondant à<br />
l’arrivée de plusieurs<br />
rayons gamma de<br />
même énergie.<br />
Signal après filtrage<br />
de déconvolution.<br />
Déconvolution à l’aveugle<br />
Cas délicat ou l’on ne connaît pas la réponse impulsionnelle du système.<br />
Exemple, restauration de vieux <strong>en</strong>registrem<strong>en</strong>ts:<br />
66<br />
68<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Obt<strong>en</strong>tion du noyau de déconvolution<br />
Domaine temporel :<br />
f ⊗ g = h<br />
Réponse<br />
impulsionnelle<br />
du détecteur<br />
Réponse<br />
impulsionnelle<br />
désirée<br />
Noyau du filtre<br />
obt<strong>en</strong>ue par TFD<br />
inverse du<br />
spectre (f)<br />
TFD<br />
TFD<br />
TFD -1<br />
Filtrage optimal<br />
Domaine fréqu<strong>en</strong>tiel :<br />
G = H / F<br />
division<br />
Problème typique : sortir un signal d’un bruit blanc aléatoire.<br />
Réponse<br />
fréqu<strong>en</strong>tielle<br />
correspondante<br />
Réponse<br />
fréqu<strong>en</strong>tielle<br />
correspondante<br />
Réponse<br />
fréqu<strong>en</strong>tielle<br />
nécessaire<br />
obt<strong>en</strong>ue par<br />
division des<br />
spectres (b) et (d)<br />
67<br />
69
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Exemples de filtres optimaux :<br />
Filtrage optimal<br />
Moy<strong>en</strong>ne mobile :<br />
Noyau = créneau.<br />
Optimise la réponse indicielle pour un niveau<br />
de réduction du bruit donné<br />
Filtrage miroir ou autocorrélation :<br />
Noyau = image symétrique du signal<br />
recherché.<br />
Optimise le rapport signal/bruit <strong>en</strong><br />
amplitude au pic<br />
Filtre de Wi<strong>en</strong>er<br />
Discrimination fréqu<strong>en</strong>tielle:<br />
2<br />
S[<br />
f ]<br />
H[<br />
f ] = 2 2<br />
S[<br />
f ] + B[<br />
f ]<br />
Optimise le rapport signal/bruit <strong>en</strong><br />
puissance.<br />
70<br />
Signaux & Systèmes - M1 Physique - <strong>LPSC</strong>/UJF - F.Montanet<br />
Exemples de filtres optimaux :<br />
Filtrage optimal<br />
Moy<strong>en</strong>ne mobile :<br />
Autocorrélation :<br />
Wi<strong>en</strong>er :<br />
71