La fonction exponentielle - Lyceedadultes.fr

Exercices 28 novembre 2013La fonction exponenetielleExercice ISimplifications Simplifer les écritures suivantes :a) (e x ) 3 e −2xb) ex−1e x+2c) ex + e −xe xd) e −x e 2 e)e 3x(e −x ) 2 × e xf) ex e ye x−yExercice IIFonctions hyperboliquesPour tout x, on pose : g(x)= ex + e −xet2a) Démontrer que [ g(x) ]2 − [h(x)] 2 = 1h(x)= ex − e −x2b) Démontrer que g(2x)=2 [ g(x) ]2 − 1 et que h(2x)=2g(x)×h(x).Exercice IIIÉquations et inéquations : Résoudre les équations ou les inéquations suivantes :1) e 3−x = 12) e 2x2 +3 = e 7x3) 2e −x =4) e x3 = e 85) e x+1 = e 1 x1e x + 26) e sin x = e 21 11) e x 1 e x7) e x2 = (e 2 ) 3 e −x8) e x2 = e x−212) (e x − 1)e x > e x − 19) e x2 1 e 213) e 2x < e x10) (e x ) 3 e x+6 14) 3(e x ) 2 + e x − 4

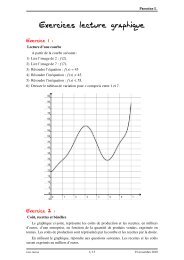
exercicesExercice VDéterminer une fonctionLa courbe ci-contre représente une fonctionf définie surRpar :A •3f (x)=(ax+b)e −x2où a et b sont deux réels.1) À l’aide des renseignements portés surla figure, déterminer a et b.2) Calculer f ′ (x). En déduire les coordonnéesdu point A maximum de f−3−2−11O−1−21 2 3 4Exercice VICalcul de limitesDéterminer les limites des fonction f suivantes à l’endroit indiqué.1) f (x)= ex − 1en 0,+∞ et−∞2x2) f (x)=2xe −x en+∞3) f (x)= ex − 1en+∞ et−∞2e x + 14) f (x)=e 2x − e x + 1 en+∞ et−∞5) f (x)=2x−1+e −x en+∞ et−∞6) f (x)= 1 x (e2x − 1) en 0 et+∞7) f (x)= x+2+ xe xDémontrer que la courbe de f admet uneasymtote oblique en−∞Exercice VIIÉtude d’une fonctionf est la fonction définie surRpar : f (x)= 2ex − 3e x + 11) Pourquoi les droite d et∆d’équation respectives y=2 et y=−3 sont-elles asymptotesà C f ?2) Calculer f ′ (x) puis étudier les variations de f .3) Tracer d,∆et C f4) La courbe semble avoir un point de symétrie. Démontrer cette conjecture.Exercice VIIIAffirmationsf est la fonction définie surRpar : f (x)=(3− x)e xJustifier les affirmations suivantes :1) Le tableau de variations de f est :paulmilan 2 Terminale S

exercicesx−∞ 2 +∞f (x)0e 2−∞2) Pour tout réel m>0 et me 2 , l’équation f (x)=m admet soit aucune, soit deuxsolutions.Exercice IXFonction gaussiennef est la fonction définie surRpar : f (x)=e −x2 .1) Calculer f (−x). Que peut-on conclure pour C f ?2) Étudier les variations de f sur [0;+∞[.3) Tracer la courbe C f dans un repère orthonormal.Exercice XCourbes tangentesDans un repère orthogonal, on a tracé cicontreles courbe C 1 et C 2 représentant lesfonctions f 1 et f 2 définies sur [0;π] par :f 1 (x)=e −x et f 2 (x)=sin x e −xDémontrer que C 1 et C 2 sont tangentes enun point A.1OC 1C 21 2 3Application au sciencesExercice XILe rayonnement d’une étoile. L’intensité I(λ) du rayonnement d’une étoile pour unelongueur d’ondeλ(λ>0), est donnée par :I(λ)= 1 λ 5 e− K λoù K est une constante positive qui dépend de l’étoile.Démontrer que l’intensité I(λ) rayonnée par l’étoile est maximale pour une valeurλ 0 deλ que l’on déterminera en fonction de K. En déduire I(λ 0 ).Exercice XIIEn économieA. Étude d’une fonctionf est la fonction définie sur I= [0;+∞[ par : f (x)= 10xe x + 1paulmilan 3 Terminale S

exercices1) Démontrer que pour tout réel x de I, on a : f ′ (x)=définie sur I que l’on déterminera.10g(x) où g est une fonction(e x + 1)22) Démontrer qu’il existe un unique réelαde I tel que g(α)=0. Donner deαun encadrementd’amplitude 10 −1 .3) En déduire le tableau de variation de f et démontrer que f (α)=10(α−1).4) Construire la courbe C de f dans un repère orthonormal d’unité graphique 2 cm.B. Application économiqueAprès avoir lancé la fabrication d’un nouvel objet, une entreprise a réalisé une étude quia montré que le coût total C T (q) en milliers d’euros pouvait être assez bien décrit par lafonction : C T : q↦−→ f (q)+q, f étant la fonction de la partie A et q le nombre d’objetfabriqués en centaines d’objets.1) Sur la figure de la partie A, représenter la courbe C T sur l’intervalle [0; 10] en justifiantvotre construction.2) A combien peut-on évaluer le coût de 300 objets ?3) Le coût unitaire est donné par C u (q)= C T(q)100q .A l’aide de la calculatrice, estimer à partir de combien d’objets fabriqués le coût unitaireest inférieur à 12e.Exercices de BACExercice XIIIAmérique du sud novembre 2013Soit f la fonction définie surRpar : f (x)= xe 1−x1) Vérifier que pour tout réel x, f (x)=e× x e x .2) Déterminer la limite de la fonction f en−∞.3) Déterminer la limite de la fonction f en+∞. Interpréter graphiquement cette limite.4) Déterminer la dérivée de la fonction f .5) Étudier les variations de la fonction f surRpuis dresser le tableau de variation.Partie BPour tout entier naturel n non nul, on considère les fonctions g n et h n définies surRpar :g n (x)=1+ x+ x 2 +···+ x n et h n (x)=1+2x+···+nx n−1 .1) Vérifier que, pour tout réel x : (1− x)g n (x)=1− x n+1 .1− xn+1On obtient alors, pour tout réel x1: g n (x)=1− x .2) Comparer les fonctions h n et g ′ n, g ′ n étant la dérivée de la fonction g n .En déduire que, pour tout réel x1: h n (x)= nxn+1 − (n+1)x n + 1.(1− x) 23) Soit S n = f (1)+ f (2)+...+ f (n), f étant la fonction définie dans la partie A.En utilisant les résultats de la partie B, déterminer une expression de S n puis sa limitequand n tend vers+∞. Vérifier cette limite par un algorithme.paulmilan 4 Terminale S

exercicesExercice XIVPondichéry avril 2013 modifiéOn s’intéresse à l’évolution de la hauteur d’un plant de maïs en fonction du temps. Legraphique ci-dessous représente cette évolution. La hauteur est en mètres et le temps enjours.On décide de modéliser cette croissance par une fonction logistique du type :ah(t)=1+be −0,04toù a et b sont des constantes réelles positives, t est la variable temps exprimée en jours eth(t) désigne la hauteur du plant, exprimée en mètres.On sait qu’initialement, pour t=0, le plant mesure 0, 1 m et que sa hauteur tend vers unehauteur limite de 2 m.Déterminer les constantes a et b afin que la fonction h corresponde à la croissance duplant de maïs étudié.Partie 2On considère désormais que la croissance du plant de maïs est donnée par la fonction f2définie sur [0 ; 250] par : f (t)=1+19e −0,04t1) Déterminer f ′ (t) en fonction de t ( f ′ désignant la fonction dérivée de la fonction f ).En déduire les variations de la fonction f sur l’intervalle [0 ; 250].2) A l’aide d’un algorithme, donner, au jour près, le temps nécessaire pour que le plantde maïs atteigne une hauteur supérieure à 1, 5 m.3) On s’intéresse à la vitesse de croissance du plant de maïs ; elle est donnée par la fonctiondérivée de la fonction f .La vitesse de croissance est maximale pour une valeur de t.En utilisant le graphique donné ci-dessous, déterminer une valeur approchée de celleci.Estimer alors la hauteur du plant.2,01,81,61,41,21,00,80,60,40,2hauteur (en mètres)y=2temps t (en jours)20 40 60 80 100 120 140 160 180 200 220paulmilan 5 Terminale S

exercicesExercice XVet C est sa courbe repré-f est la fonction définie surR−{−1} par : f (x)=e −x + 1− x1+ xsentative dans un repère orthonormal.1) Étudier les limites de f aux bornes de son ensemble de définition.2) Étudier les variations de f .3) Tracer la courbe C .Exercice XVIf 0 et f 1 sont deux fonctions définies surRpar : f 0 (x)= exet f1+e x 1 (x)=C 0 et C 1 sont leurs courbes représentatives dans un repère orthonormal.11+e x1) On a tracé ci-contre C 0 et C 1 . Attribuerà chaque fonction sa courbe en justifiantvotre réponse.(2) Le point A 0, 1 )est-il centre de symétrie pour les deux courbes ?23) Par quelle transformation simple, C 1 est-elle l’image de C 0 ?4) Vérifier que pour tout réel x on a : f 0 (x)+ f 1 (x)=1.5) En déduire que C 1 est l’image de C 0 par une autre symétrie.−2−11OA•1 2Exercice XVIIf est la fonction définie sur ]0;+∞[ par : f (x)= ex − 1x1) Dans un repère orthonormal, construire la courbeΓd’équation y=e x et la droite dtangente àΓen x=0.2) Justifier graphiquement que, pour tout réel u : e u u+13) En déduire que pour tout réel x : e −x + x−10 et 1+(x−1)e x 04) Démontrer alors que la fonction f est strictement croissante sur ]0;+∞[.Exercice XVIIIf est la fonction définie surRpar : f (x)= x− ex − 1e x + 11) Vérifier que pour tout réel x : f (x)= x−1+ 2e x + 12) Étudier les limites en+∞ et−∞.3) Démontrer que f est impaire.4) Étudier les variation de f sur [0,+∞[.5) Tracer la tangente à C au point d’abscisse x=0, puis la courbe C .etf (x)= x+1− 2exe x + 1paulmilan 6 Terminale S