Chapitre 11 Rotation d'un corps rigide autour d'un axe fixe
Chapitre 11 Rotation d'un corps rigide autour d'un axe fixe
Chapitre 11 Rotation d'un corps rigide autour d'un axe fixe
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
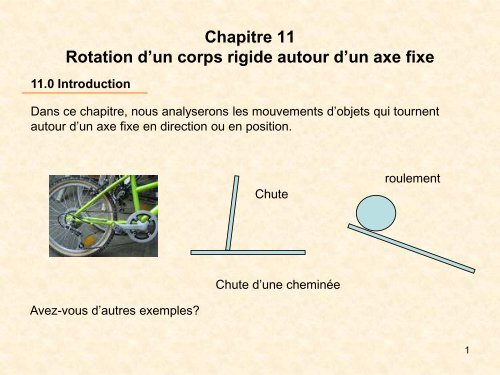
<strong>Chapitre</strong> <strong>11</strong><strong>Rotation</strong> d’un <strong>corps</strong> <strong>rigide</strong> <strong>autour</strong> d’un <strong>axe</strong> <strong>fixe</strong><strong>11</strong>.0 IntroductionDans ce chapitre, nous analyserons les mouvements d’objets qui tournent<strong>autour</strong> d’un <strong>axe</strong> <strong>fixe</strong> en direction ou en position.ChuteroulementChute d’une cheminéeAvez-vous d’autres exemples?1
<strong>Chapitre</strong> <strong>11</strong><strong>Rotation</strong> d’un <strong>corps</strong> <strong>rigide</strong> <strong>autour</strong> d’un <strong>axe</strong> <strong>fixe</strong><strong>11</strong>.0 IntroductionGrande roue, roues de bicyclette stationnaire ou en roulement , rotationde la Terre <strong>autour</strong> de son <strong>axe</strong>, rotation des CD, DVD, boule de quille,manivelle, portes, moteurs, satellites en rotation <strong>autour</strong> de leur <strong>axe</strong>.Nous traiterons:la cinématique ( description, variables angulaires ) des mouvements derotation ,la dynamique (cause, lois de Newton)les principes de conservation: énergie et quantité de mouvement.Bref, nous reverrons l’ensemble des concepts ou grandeursphysiques que nous avons abordés depuis le début du cours pour latranslation.2
<strong>Chapitre</strong> <strong>11</strong><strong>Rotation</strong> d’un <strong>corps</strong> <strong>rigide</strong> <strong>autour</strong> d’un <strong>axe</strong> <strong>fixe</strong><strong>11</strong>.0 IntroductionQuels genres de mouvements analyserons-nous? Quellesseront les équations utiles pour décrire le mouvement?Nous étudierons les mouvements circulaires uniformes (MCU)à vitesse constante et les mouvements circulairesuniformément accélérés (MCUA), combinées avec de latranslationNous avons déjà analysé en partie ces types demouvements en utilisant des variables linéaires, nousutiliserons cette fois des variables angulaires.3
<strong>11</strong>.0 IntroductionDans les cas où nous aurons une accélération angulaire constante,nous aurons un MCUA. Les équations du mouvement seront de lamême forme qu’un m.r.u.a soit :Pour la position angulaireθ = θ + ωot+oPour la vitesse angulaire1α t22ω = ω o + αtω ( ω + ω) /moy= oθ 02En fonction dudéplacementangulaireω22o= ω + 2α∆θNous utiliserons ces équations pour décrire le mouvement d’objets quitournent avec une vitesse angulaire variable <strong>autour</strong> d’un <strong>axe</strong> de rotation quidemeure <strong>fixe</strong>.4
<strong>11</strong>.1 Cinématique de rotationQuelles définitions de variables angulaires et d’équations dumouvement de rotation allons-nous prendre?Prenons par exemple le mouvementde rotation d’une roue de bicyclette<strong>autour</strong> d’un <strong>axe</strong> <strong>fixe</strong>A) Position angulaire thêta θ (rad)Sens positif anti-horaireyRθs+Par définitionθ = s / Rx5
<strong>11</strong>.1 Cinématique de rotationy+A) Position angulaire thêtaθ (rad)Sens positif anti-horairePar définitionθ =sRRθsx1 rad = 57,3 oB) Déplacement angulaire delta thêta ∆θ (rad)Par définition :∆ θ = ( θ −θ)o=∆sRUn tour ou une circonférence2πrad6
<strong>11</strong>.1 Cinématique de rotationB) Déplacement angulaire ∆θ(rad)∆ θ = ( θ −θ)o=∆sRyπ2radxRelation avec les variables linéairesUn tour ou une circonférence :∆s=C= 2πRUn quart de tour ou un quartde circonférenceπ2radC) Vitesse angulaire oméga ω rad/sPas de tours par minute ou tours par seconde dans les équations.7
<strong>11</strong>.1 Cinématique de rotationC) Vitesse angulaire oméga moyenneω rad/syωdéfinitionθ θ -ω = ∆moy=∆ t t - tθ oorad/sxD) Vitesse angulaire oméga ω rad/sωégale la dérivée de laposition angulaire par rapport autempsω =dθdtrad/sPositif sens antihoraireen généraldéfinition8
<strong>11</strong>.1 Cinématique de rotationD) Vitesse angulaire oméga ω rad/syωωégale la dérivée de laposition angulaire par rapport autempsω =dθdtrad/sOrientation du vecteur vitesseangulaire omégaySur l’<strong>axe</strong> de rotationXxPositif sens anti-horaire engénéralωpoucexdoigtsRègle de la main droiteHYperphysics<strong>Rotation</strong>, angular velocity, vector9
<strong>11</strong>.1 Cinématique de rotationLorsque la vitesse angulaire oméga ω est constante nousaurons un mouvement circulaire uniforme MCUQuelle sera l’équation du mouvement ?Selon la définition de lavitesse moyenne nous auronsyω∆θθ -ω ωmoy= = =∆tt - tθ oorad/sÉq. MCUθ θ o+ ωtrad= Avec t o =0On définit également la fréquence f par le nombre de tours ou derévolutions par seconde comme l’inverse de la période T le tempspour un tourf1=T10
<strong>11</strong>.1 Cinématique de rotationDans un MCU, on utilise la relation suivante pour distinguerentre la vitesse angulaire « ω » et la fréquence angulaire «f »2 πω = = 2πfTRelation entre les variables linéaire et angulaire :v tPar définitions =RθωRVitesse tangentielledsdt=dθRdtv t= ωR<strong>11</strong>
<strong>11</strong>.1 Cinématique de rotationRelation entre les variables linéaire et angulairev tRPar définitions =dsdt=RθdθRdtωAlors, vitesse tangentiellev t= ωRAinsi, plus une particule est située loin de l’<strong>axe</strong> de rotation ,plus sa vitesse tangentielle est grande pour une même vitesseangulairev t= ωrv trω12
<strong>11</strong>.1 cinématique de rotationLorsque la vitesse angulaire varie nous aurons besoin deE) Accélération angulaire moyenne alpha α rad/s 2αmoy=ω −ωot − to2rad/sF) Accélération angulaire alpha α rad/s 2α =dωdt2rad/sLorsque la roue tourne de plus en plus vitesse, α et ω sontdans le même sens si non ces vecteurs sont en sens contraires13
<strong>11</strong>.1 cinématique de rotationωαAccélérationangulaire positive.⊗Augmentation de lavitesseωαAccélérationangulaire négativeDiminution de lavitesseVu defaceω et α sortent•Vu de face ω sort α entre•X14
<strong>11</strong>.1 cinématique de rotationRelation ente les variables angulaire et linéaire :v tv ROn a vu que t= ωωαRdoncAccélération tangentielledv tdt=dωRdta t= αRv ta tωa rRAccélérationradiale=2vR= ω Ra r2αAccélération linéaire2a = a +r2a t15
<strong>11</strong>.1 cinématique de rotationRelation ente les variables angulaire et linéaireωa tRAccélérationradialeAccélérationtangentiellea t= αR=2vR= ω Ra r2αa ta tu θAccélération linéaire2a = a +r2a tωa rRu ra= −arur+a u θt2m/sαDéjà vu au chapitre 416
<strong>11</strong>.1 cinématique de rotationExemple : Vous montez un seau d’eau d’un puits commel’indique la figure ci-dessous. Le rayon du cylindre est de 5 cm.Partant du repos, le seau atteint 4 m/s après 1,0 m de montée.SituationDéterminez :A) L’accélération angulaire ducylindreProblème: Je cherche αSolution possiblea t= αRα =a tR17
<strong>11</strong>.1 cinématique de rotationExemple : Vous montez un seau d’eau d’un puits comme l’indique lafigure ci-dessous. Le rayon du cylindre est de 5 cm. Partant du repos,le seau atteint 4 m/s après 1,0 m de montée.SituationProblème: Je cherche αSolution possiblea t= αRα =a tRPour le seau, nous avons un m.r.u.aD’oùv22= v + 2aot∆ya t=2v2∆y=162=8m/s218
<strong>11</strong>.1 cinématique de rotationSituationPour le seau, nous avons un m.r.u.aD’oùa t=2v2∆yv2=2= v + 2a162=o8m/s2t∆ya t8α = = = 160R 0,052rad/sRésultat probable L’accélération angulaire du cylindre est de 160rad/s 2Pour sa part, la vitesse angulairefinale sera donnée parv t4ω = = =R 0,0580rad/s19
<strong>11</strong>.1 cinématique de rotationSituationRésultat probable L’accélérationangulaire du cylindre est de 160 rad/s 2Celui-ci sera donné parPour sa part, la vitesse angulaire finale seradonnée parv t4ω = = =R 0,05B) Déterminez le nombre de tours effectué par le cylindre.B)Nb=1,0 mC = 2πR80rad/sC = 2 πR = 2×3,14×0,05 = 0,314 m 1,0 mNb = = 3, 180,31420
<strong>11</strong>.1 cinématique de rotationSituationC) Déterminez la vitesse angulairemoyenne ω moyLa vitesse angulaire moyenne sera donnée parωmoy=∆θ=∆tω + ω( i f2)Puisque l’accélération angulaire est constanteωmoy=( ω + ωi2f) (0 + 80)= =240rad/sRésultat probable : La vitesse angulaire moyenne sera de 40 rad/s21
<strong>11</strong>.1 Cinématique de rotationEn résumé, dans les cas où nous aurons une accélération angulaireconstante, nous aurons un MCUA. Les équations du mouvementseront de la même forme qu’un m.r.u.a soit :Pour la position angulairePour la vitesse angulaireθ = θ + ωot+oω = ω o + αt1α t2ω ( ω + ω) /moy= o22En fonction dudéplacementangulaireω22o= ω + 2α∆θNous utiliserons ces équations pour décrire le mouvement d’objets quitournent avec une vitesse angulaire variable <strong>autour</strong> d’un <strong>axe</strong> de rotation quidemeure <strong>fixe</strong>.22
<strong>11</strong>.1 Cinématique de rotation RésuméSchéma avec les définitions et les variables de lacinématique de rotation et les liens avec les variables de latranslationPour la position angulaire θ rad Pour la vitesse angulaire ω rad/sAccélération angulaire α rad/s 2∆s∆s=R∆θÉquations ;∆θRv t = ωRm.c.ua t = αRm.c.u.aÀ compléter23