DS_Lec9_20101213

2010/12/13 第9回
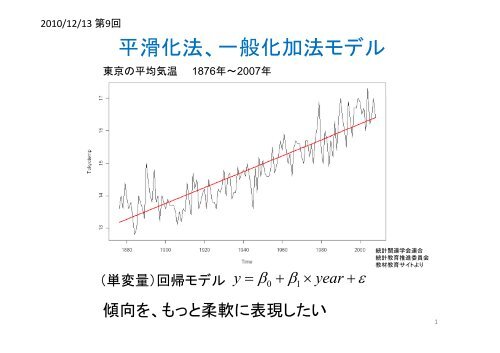
平滑化法、一般化加法モデル
滑 法、 般 法
東京の平均気温 1876年~2007年
(単変量)回帰モデル
y 0 1
year
傾向を、もっと柔軟に表現したい
統計関連学会連合
統計教育推進委員会
教材教育サイトより
1

2010/12/13 第9回
移動平均法
(2m+1)項移動平均:当期と前後m期の合計(2m+1)期の
平均を当期の移動平均値とする
21項移動平均
東京の平均気温 1876年~2007年
2

2010/12/13 第9回
移動平均法:局所的な平均
局所重み付き回帰法
局所重み付き回帰法
局所的 局所的に多項式回帰モデルをあてはめる
多項式回帰 デ をあ はめる
x x
の近傍で局所的に = に近いほど大きな重み、
遠い値には0の重み、を付けて
多項式を最小2乗法であてはめる
2 x x y f x )
w
i
i ( i ⇒ 最小化
f (x)
:多項式関数
(直線、2次曲線、…)
直線 次曲線
3

2010/12/13 第9回
局所重み付き回帰法
東京の平均気温 1876年~2007年
関数 loess による
あてはめ
4

2010/12/13 第9回
関数 loess
局所重み付き多項式回帰法により曲線(曲面)をあ 局所重み付き多項式回帰法により曲線(曲面)をあてはめる はめる
loess(formula, data, weights, subset, na.action, span = 0.75,
enp.target, ddegree = 2, parametric = F, ddrop.square
= F,
normalize = T, family = c("gaussian", "symmetric"), model = F,
control control, ...) )
誤差に正規分布を 誤差に正規分布を仮定せず、
仮定する.重みの再計算 重みの再計算を繰り返して、
をしない(デフォルト) 頑健なあてはめを行う
formula モデル式 をしない(デフォルト)
data 用いるデータフレーム(指定は任意)
span 平滑の度合いをコントロールするパラメータ
平滑の度合いをコントロールするパラメータ.
大きいほど滑らかな曲線になる. デフォルトは 0.75
degree あてはめる多項式の次数 あてはめる多項式の次数. デフォルトは2次
デフォルトは2次.
どの平滑化手法も、平滑の度合いをコントロールするパラメー
タの値によって、結果が大きく異なることに注意.
5

2010/12/13 第9回
関数 loess: パラメータspan ラ タ p の値による違い
値 る違
6

2010/12/13 第9回
平滑化スプライン法
平滑化 ライ 法
f (x)
3次スプライン関数
2階までの導関数が連続な 2階までの導関数が連続な、区分的3次多項式
区分的3次多項式
, , x x
, 2
x
x x
• 節点(knots): 1 m 1 2
m
• 各 各区間 間 [ , x 1 ] ( k 1 1,...,
m 1 ) で3次多項式 次多項式 f ( (x )
xk k
m 1
f ( x)
I[
x x ] ( x)
fk
f ( ) [ x ] ( ) f
k , xk1
k
k 1
;
( x )
• 各節点(端点を除く)で2階までの導関数が 連続
f
k 1
f
f
k 1
k 1
( x
( x
( x
k
k
k
)
)
)
f
k
k
( x
f ( x
f (
x
k
k
k
k
)
) ,
)
k
2 , , m 1
x
f k
7

2010/12/13 第9回
節点での値を f ( x ) ( k 1 ,..., m ) と固定したとき
y k k
• m‐1個(区関数)の3次多項式 4(m‐1) パラメータ
• 節点(区間の両端点)での制約 2(m‐1) 2(m 1)
• 1階微分の連続性の制約 m‐2
• 2階微分の連続性の制約 m‐2
⇒ 4(m‐1) –{2(m‐1)+m‐2+m‐2} = 2個の自由度が残る
2個の自由パラメータをどう定めるかでいろいろなスプライン関
数がある
• 自然スプライン(natural spline) f ( x 1 ) f
( x m ) 0
• B‐スプライン(B‐spline, B for Basic)(両端に任意の3節点を加える)
B
B
m 3
i1
( 3)
f ( x ) B ( x )
( d )
i
( 0)
i
i
x xi
( x)
x x
id
1
1 xi
x x
( x)
0
その他
i
i
B
i1
( d 1)
i
x
( x)
x
id
id
x
x
i
B
( d 1)
i1
( x)
i 1,...,
m
d
0,
1,
2
8

2010/12/13 第9回
平滑化と補間
平滑化 補間
補間 (interpolation) 、補外(extrapolation)
– 観測されていない値を補う
– 観測された点は通らなければならない
x に対する y の値を補う場合、
補間は観測された値の範囲内の x に対する y を補い、
補外は観測された値の範囲外の x に対する y を補う。
平滑曲線は 平滑曲線は、観測された点を通るわけではない。
観測された点を通るわけではない
y
f (x)
f ( (x ) は y の‘傾向’を表す滑らかな曲線
9

2010/12/13 第9回
平滑化スプライン法
平滑化 ライ 法
• 3次平滑化スプライン法は、罰則付き残差2乗和
n
y f x )
2
2
i ( i f (
x)
dx
i1
データの当てはまり
具合を表す
関数のでこぼこに
対するペナルティー
(roughness penalty)
を最小にするスプライン曲線を平滑化関数とする方法。
• はデータへの当てはまり具合と関数の滑らかさのバラン
スをコントロ スをコントロールするパラメータで平滑化パラメータ
ルするパラメ タで平滑化パラメ タ
(smoothing parameter) と呼ばれる。
• が大きいほど が大きいほど、滑らかな曲線が得られる。
滑らかな曲線が得られる
10

2010/12/13 第9回
関数 smooth.spline p
B‐スプライン関数による平滑化スプライン曲線を当てはめる
smooth smooth.spline(x, spline(x yy, w = below>>, df = below>>,
spar = 0, cv = F, all.knots = F, df.offset = 0, penalty = 1)
x 予測変量
y 反応変量
df 等価自由度 等価自由度. これを用いても滑らかさを制御できる
これを用いても滑らかさを制御できる。
spar と同等の平滑化パラメータ. 滑らかさについての指
定がない場合は、一般化交差検証法(GCV)で自動的に選択
定がない場合は、 般化交差検証法(GCV)で自動的に選択
される。
等価自由度: 等価 度 平滑化スプライン法による推定値ベクトルは、観
滑 ラ 法 推定値 、観
測値ベクトルの線形結合として yˆ My と表現でき、行列 M
は疑似射影行列とみなせる。この対角和 tr(M)
が等価自由度
11

2010/12/13 第9回
Tokyotemp T
Tokyoteemp
平滑化スプライン法による平滑曲線
平滑化 ライ 法 る平滑曲線
17
15 16
13 14
16 17
13
14 15
GCV(spar=0.0254)
1880 1900 1920 1940 1960 1980 2000
Time
spar=1
1880 1900 1920 1940 1960 1980 2000
Time
Tokyotemp T
17
15 16
13 14
spar=0.000001
1880 1900 1920 1940 1960 1980 2000
Time
> smooth.spline(Tttime, p ( Tokyotemp) y p)
Call:
smooth.spline(x = Tttime, y = Tokyotemp)
Smoothing Parameter (Spar): 00.02544036 02544036
Equivalent Degrees of Freedom (Df): 4.018848
Penalized Criterion: 26.63255
GCV: 0.2073451
>
12

2010/12/13 第9回
一般化加法モデル
GAM GAM, GGeneralized li dAdditi Additive MModel d l
一般化線形モデル
X X
g
g ( ) 0 1 1 2 2
Y
一般化加法モデル
~ 指数型分布 ,
E[Y ]
g
)
f ( X )
f ( X )
p p X p p
( 0 1 1 2 2 f p ( X p
Y
~ 指数型分布 ,
f X ), f ( X ), ,
1( 1 2 2 f p ( X p
)
E[Y ]
:平滑化関数
)
13

2010/12/13 第9回
一般化加法モデルの当てはめ
般化加法 デ 当
gam(formula = formula(data), family = gaussian, data = , weights h = , subset b = ,
na.action = na.fail, start = , control =
gam gam.control(...), control( ) trace = FF, model = FF, x = FF, y = TT, qr = F, F
method = "qr", contrasts = NULL, ...)
引数は glm とほとんど同じ.大きな違いは、formula に与えるモ
デル式の右辺に lo, s, bs, ns などの平滑化関数を指定できる
こと.
• 局所回帰(loess)関数 lo(…, span=0.5, degree=1)
• 平滑化スプライン関数(smoothing spline) s(x, df=4, spar=0)
• B‐スプライン関数 (basic spline) bs
• 自然スプライン関数(natural spline) ns
14

2010/12/13 第9回
partial residualls
脊椎後湾症データへの一般化加法モデルのあてはめ
脊椎後湾症デ タ の 般化加法モデルのあてはめ
1 2
-3 -22
-1 0
0 50 100 150 200
partial residualls
AAge
St Startt
2
-6 -4 - -2 0
5 10 15
>kypho.gam = gam(Kyphosis ~ s(Age,4) +s(Start)+ Number, family =
binomial binomial, data = kyphosis)
>kyphopdt = predict(kypho.gam,type='terms')
>plot(Age, plot(Age, kyphopdt[,1]+residuals(kypho.gam), kyphopdt[,1] residuals(kypho.gam), ylab="partial ylab partial residuals residuals") )
>lines(Age[order(Age)], kyphopdt[order(Age),1],col=3,lwd=2)
>plot(Start, kyphopdt[,2]+residuals(kypho.gam),ylab="partial residuals")
>lines(Start[order(Start)], ( [ ( )], kyphopdt[order(Start),2],col=3,lwd=2)
yp p [ ( ), ], , )
15

2010/12/13 第9回
燃費データへの一般化加法モデルのあてはめ
燃費
0.12
0.10
0.08
2000 3000 4000 5000
排気量
>attach(fuel)
>fuel.gam= gam(Fuel~lo(Disp.), data=fuel)
>plot(Disp., Fuel,xlab='排気量',ylab='燃費')
>lines(Disp.[order(Disp.)], predict(fuel.gam)[order(Disp.)],col=3,lwd=2)
16