SIMMETRIE NEL PIANO CARTESIANO

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
SIMMETRIE NEL PIANO CARTESIANO
SIMMETRIE RISPETTO AGLI ASSI CARTESIANI
ASSE X: P x, y P x, y
( ) a ( − ) ; punto medio: M ( x,0
)
ASSE Y: P x, y P x, y
1
( ) a ( −
) , punto medio: M ( 0, y )
2
La simmmetria rispetto ad un asse è quella
trasformazione che associa a ciascun punto un
altro punto tale la retta che li congiunge sia
perpendicolare all'asse di simmetria ed il punto
medio di essi vi appartenga.
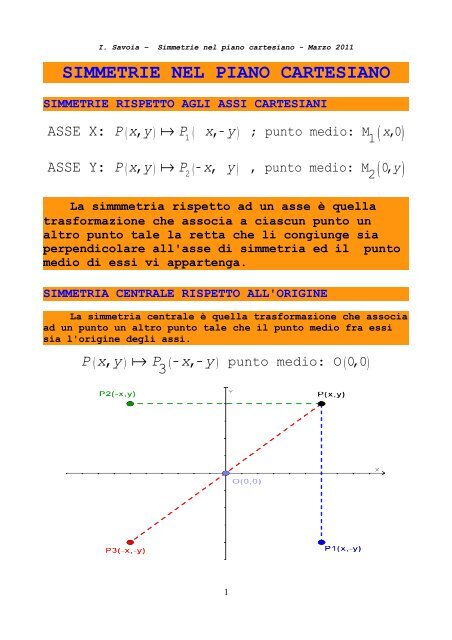
SIMMETRIA CENTRALE RISPETTO ALL'ORIGINE
La simmetria centrale è quella trasformazione che associa
ad un punto un altro punto tale che il punto medio fra essi
sia l'origine degli assi.
P ( x, y ) a
P ( − x, − y ) punto medio: O ( 0,0
3
)
1
1
2

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
Ad ogni punto del piano corrisponde un suo simmetrico
rispetto a ciascuno dei due assi cartesiani per cui, ad ogni
insieme di punti appartenente ad una data figura geometrica,
luogo geometrico e grafico di funzione matematica,
corrispondono rispettivamente, insieme di punti simmetrico
della figura, del luogo geometrico e del grafico di funzione.
In figura i triangoli simmetrici di un triangolo dato.
FUNZIONI SIMMETRICHE E LORO GRAFICI.
I grafici simmetrici delle funzioni, per
esempio retta e parabola, si costruiscono a
partire dalle loro espressioni che sono state
modificate con la sostituzione delle variabili
cambiate di segno, in base alle simmetrie.
Illustriamo di seguito esempi di rette e
simmetriche e di parabole simmetriche.
2

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
1) rette simmetriche della retta di equazione:
r: y = 2x − 6
⎡x →
Asse X: ⎢
⎢ y →
x ⎤
⎥
− y ⎥ a r:-y = 1 2x − 6 a y = − 2x + 6
⎢⎣ ⎥⎦
⎡ x →
Asse Y: ⎢
⎣
y →
− x ⎤
r:
y 2 y ⎥ a
=
⎦
− 2x − 6
⎡ x →
Origine: ⎢
⎣
y →
− x ⎤
− y
⎥
⎦
a r : − y =
3
− 2x − 6 a
y = 2x + 6
Rappresentazione grafica delle rette simmetriche:
3

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
2) Parabole simmetriche della parabola di equazione :
y = x2 - 4x + 3
⎡ x → x ⎤
Asse X : ⎢
y y
⎥
⎣
→ −
⎦
a − y = x2 - 4x + 3 a y = -x2
+ 4x − 3
⎡ x →
Asse Y: ⎢
y →
⎣
− x ⎤
y
⎥
⎦
a y = x 2 + 4x + 3
⎡ x →
Origine : ⎢
⎣
y →
− x ⎤
− y
⎥
⎦
a − y = x2
+ 4x - 3 a y = -x2 - 4x + 3
Rappresentazione grafica delle parabole simmetriche:
Esercizio: determinare, per ciascuna delle due seguenti
funzioni, le tre simmetriche rispetto agli assi e all'origine
e costruirne i rispettivi grafici nello stesso disegno.
a) -2x+3y+4=0 ; b) y=-2x2 +
6x
4

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
SIMMETRIA DELLE FUNZIONI: PARITA' E DISPARITA'
Esistono funzioni matematiche definite da formule
che, rispetto ai cambiamenti dei segni dovuti alle
simmetrie, hanno peculiari proprietà che qui definiamo:
Simmetria pari:
( ) = ( − )
Esempio di funzione pari:
f ( x ) = 2x2 − 8 a f ( − x ) = 2 ( − x )
2
− 8 = 2x2 − 8
Simmetria dispari:
( − x ) = -f
( x )
Esempio di funzione dispari:
f ( x ) = 2x3 − 8x a f ( − x ) = 2 ( − x )
3
− 8 ( − x ) = − 2x3 + 8x = − 2x3 − 8x
Nessuna simmetria:
f x f x
f
f
( − x ) ≠ ± f ( x )
Esempio di funzione non simmetrica:
f ( x ) = 2x2 − 8x a
f ( − x ) = 2 ( − x )
2
− 8 ( − x ) = 2x2 + 8x
≠ ± f ( x )
Funzioni pari: formule e grafici rimangono invariati
rispetto alla simmmetria di asse Y verticale per cui i
grafici sono composti da due parti specularmente uguali
da parti opposte rispetto all'asse Y
Funzioni dispari: formule e grafici rimangono
invariati rispetto alla simmetria centrale per cui i
grafici sono composti da due parti specularmente uguali e
da parti opposte rispetto all'origine, il primo ed il
terzo quadrante oppure il secondo ed il quarto quadrante.
Funzioni non simmetriche: formule e grafici cambiano
a seguito delle trasformazioni di simmetria.
5
⎛ ⎞
⎜ ⎟
⎝ ⎠

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
FUNZIONI MATEMATICHE E SIMMETRIE
Le funzioni reali di variabile reale sono delle leggi
di corrispondenza univoche, definite da formule
matematiche, che associano ad ogni valore numerico della
variabile indipendente X nell'insieme dei nueri reali R
o di suoi sottoinsiemi detto dominio D, dei valori
numerici reali di variabile dipendente Y che
costituiscono l'insieme detto codominio.
Definiamo meglio il concetto di univocità delle funzioni:
ad ogni valore della variabile indipendente X del dominio
viene associato, dalla formula che definisce la funzione, uno
ed uno solo valore della variabile dipendente Y.
Il simbolo od il valore della variabile indipendente x
entro la parentesi prende il nome di argomento.
Tra le più comuni funzioni matematiche di tipo algebrico
vi sono la funzione lineare che definisce la retta, la
funzione quadratica che definisce la parabola, la funzione
omografica che definisce l'iperbole equilatera, la funzione
valore assoluto. Esaminiamole di seguito dal punto di vista
della proprietà di simmetria che si ricavano dalle formule.
Funzione lineare: definisce la retta obliqua ed orizzontale.
f ( x ) = m ⋅ x + q a f ( − x ) = m ⋅ ( − x ) + q = − m ⋅ x + q
Se q ≠ 0 la retta non passa per l'origine e la funzione
è priva di simmetria.
Se q = 0 la retta passa per l'origine e
la funzione ha simmetria dispari: a
f ( − x ) = − m ⋅ x = − f ( x )
Funzione quadratica: definisce la parabola ad asse verticale
Un trinomio di secondo grado costituisce la formula della
parabola verticale e, in base ai valori dei suoi
coefficienti, può avere simmetria rispetto all'asse Y.
6

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
f ( x ) = ax2 + bx + c a f ( − x ) = ax2 − bx + c
Se b ≠ 0 a f ( − x ) ≠ f ( x ) nessuna simmetria
Se b = 0 a f ( − x ) = f ( x ) simmetria pari
Le parabole prive del termine di primo grado hanno il
vertice posizionato lungo l'asse Y che le divide in due parti
specularmente uguali.
Funzione omografica:
E' una funzione fratta definita da quattro coefficienti per
cui numeratore e denominatore sono binomi di primo grado:
f ( x
a x b
) =
⋅ +
, c ≠ 0
c ⋅ x + d
f
a x b a x b
( − x ) =
− ⋅ +
=
⋅ −
−c ⋅ x + d c ⋅ x − d
Se a = 0 e d = 0 la funzione è
l'iperbole equilatera ed ha simmetria dispari:
f ( x
b b b
) = → f ( − x ) = = −
c ⋅ x −c ⋅ x c ⋅ x
Funzioni con moduli: definite per mezzo dela funzione modulo.
Valore assoluto: simmetria pari
funzione elementare che associa ad ogni numero reale il
numero stesso se esso è positivo o nullo mentre associa il
suo opposto se esso è negativo e la sua simmetria è
evidentemente pari.
f ( x ) = x : x =
Rapportounitario: simmetria dispari
funzione che associa ad ogni numero reale il rapporto fra il
suo valore assoluto ed il numero stesso: è pari ad uno se il
numero è positivo o nullo ed è pari al suo opposto se il
numero è negativo e la simmetria è evidentemente dispari.
7
x , x ≥ 0
− x , x <
0

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
Rapprentazione grafica del valore assoluto e del rapporto unitario:
Funzione f(|x|): simmetria pari.
La caratteristica del grafico è quella di
eliminare, dal grafico della funzione di partenza,
la parte posta nel sempipiano sinistro dei valori
negativi della variabile indipendente x della
funzione di origine f(x).
Funzione |f(x)|: simmetrica rispetto all'asse X
Esempio:
f ( x )
x x
= , =
x x
( ) ( )
=
x
x
= + 1 , x ≥ 0
=
− x
x
= − 1 , x < 0
Es.: f x =2x2-8x ; f x = 2x2 − 8 x =
f ( x )
=
f ( x ) , f ( x ) ≥ 0
−
f ( x ) , f ( x )

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
f ( x ) = 2x2 − 8 x, f ( x ) = 2x2 − 8x
=
La caratteristica del grafico è quella di
eliminare, dal grafico della funzione di partenza,
la parte posta nel sempipiano inferiore dei valori
negativi della y della funzione di origine f(x).
Rappresentazione grafica delle funzioni con il modulo:
Esercizi sulla proprietà di simmetria delle funzioni:
1] Utilizzare la definzione di parità, disparità ed asimmetria per
verificare la proprietà di ciascuna funzione esplicitata:
2] Per ogni funzione determinare le due funzioni definite con il
modulo e rappresentare tutte e tre in grafici differenti, tramite
tabelle di numeri, verificando le proprietà di simmetria come
illustrato nelle precedenti figure:
9
2x2 − 8 x, 2x2 − 8x ≥ 0
− 2x2 + 8 x, 2x2 − 8x < 0
3
a) f ( x ) =
x − 2x
: dispari ;
x2 + 1
b) f
3 5
( x ) =
x +
: funzione asimmetrica ;
4 − x2
3 4
c) f ( x
x
) = : funzione pari ;
2x2 +
1

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
= =
a) f ( x ) = 2x − 3 ; f ( x ) = ; f ( x ) =
= =
= =
b) f ( x ) = − 2x2 + 6 x ; f ( x ) = ; f ( x ) =
= =
= =
c) f ( x
6
) = ; f ( x ) = ; f ( x ) =
x
= =
SIMMMETRIA RISPETTO A RETTE PARALLELE AGLI ASSI
Simmetria rispetto ad assi verticali e orizzontali
Le seguenti equazioni di simmetrie garantiscono che, in
base alla definizione generale, il punto medio di punti
simmetrici appartenga all'asse del loro segmento.
Simmetria di asse verticale con equazione x = a :
P( x, y) a P ( 2 a − x, y )
Simmetria di asse orizzontale con equazione y = b :
P( x, y) a P ( x,2b − y )
Es.: determiniamo le rette simmetriche rispetto
agli assi indicati delle rette seguenti:
a) y=2x+1 ; asse: x = 2
y=
xa4− x
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢y ay
⎥
⎢ ⎥
⎣ ⎦
2x+1 ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯→ y = 2 ( 4 − x ) + 1 a y = − 2x + 9
3
b) y= x-2 ; asse: y = 3
4
xax ⎡ ⎤
⎢ ⎥
⎢y a6−
y ⎥
⎣ ⎦
3 3 3
y= x-2 ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯→ 6 − y = x − 2 a
y = − x + 8
4 4 4
10

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
Rappresentazione grafica delle rette e delle loro simmetriche
degli esempi trattati:
Si osservi, come appare anche dalla raffigurazione degli
esempi visti, che esiste un punto che appartiene ad entrambe
le rette associate nella simmetria e che appartiene
necessariamente anche all'asse di simmetria: tale punto è
detto "unito".
SIMMETRIA RISPETTO ALLE BISETTRICI
Punti simmetrici rispetto alla bisettrice "y=x"
xay ⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢y ax
⎥
⎢
⎣
⎥
⎦
⎛
( , ) ( , ) M
x y
1 1
,
y x ⎞
P X Y ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯→ P y x a
+ +
⎜ ⎟
⎝ 2 2 ⎠
Il punto medio M del segmento PP 1
1
appartiene alla bisettrice avendo coordinate uguali.
Punti simmetrici rispetto alla bisettrice "y=-x"
xa− y
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢y a−
x ⎥
⎢
⎣
⎥
⎦
⎛
( , )
2
( , ) ; M
x y
2
,
y x ⎞
P x y ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯→ P − y −x
− −
⎜ ⎟
⎝ 2 2 ⎠
Il punto medio M
2
del segmento PP
2
appartiene alla
seconda bisettrice avendo coordinate opposte.
11

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
Rette simmetriche delle due bisettrici.
Per ottenere le equazioni delle rette
simmetriche delle bisettrici si dovono sostituire
le equazioni associate come nell'esempio seguente:
x a y
⎡ ⎤
⎢ ⎥
⎢ y a x ⎥
⎢⎣ ⎥⎦
Es.: y = 2x − 3 2 3
1
⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ → x = y − a y = x +
2
L'equazione ottenuta rappresenta la retta
simmetrica della retta data rispetto alla
bisettrice del primo e del terzo quadrante.
Otteniamo ora la retta
simmetrica della
retta
data rispetto alla seconda bisettrice:
xa − x
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ya − y ⎥
⎢
⎣
⎥
⎦
y = 2x − 3 x 2y 3 y
1
x
3
⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯→ − = − − a
= −
2 2
Data una qualsiasi funzione invertibile, lo scambio delle
variabili e la successiva esplicitazione della variabile
indipendente scambiata, determina la funzione inversa che, di
conseguenza, possiede la proprietà di essere simmetrica della
funzione data rispetto alla bisettrice del primo e del terzo
quadrante.
Le due figure che seguono rappresentano, dell'esempio,
rispettivamente una funzione lineare e la sua funzione iversa
simmetriche fra loro rispetto alla bisettrice del primo e del
terzo quadrante e, la seconda a destra, la retta simmetrica
rispetto alla seconda bisettrice.
12
3
2

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
SIMMETRIA RISPETTO AD ASSE OBLIQUO
Deduciamo le leggi di trasformazione che ad ogni
punto del piano associano il suo punto simmtrico
da parte opposta di una retta del tipo "y=mx+q".
Introduciamo tali leggi per mezzo di un
esempio: determinare il punto simmetrico P1(X1,Y1)
del punto P(-7,8) rispetto alla retta di equazione
"y=2x-3": occorre notare che, in base alla
definizione generale di simmetria rispetto ad un
asse, valgono due condizioni che devono essere
poste in forma di equazioni:
a) Il coefficiente angolare della retta che
passa per i due punti simmetrici deve essere
antireciproco di quello dell'asse di simmetria
poichè le due direzioni sono perpendicolari:
y − y
1 1 8 − y
= − a
1 = −
1
x − x
1
m − 7 − x
1
2
b) Il punto medio del segmento che ha per
estremi i due punti simmetrici deve appartenere
all'asse di simmetria:
13

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
y + y
1
x + x
1
8 + y
1
− 7 + x
= m + q a
= 2 1 + 3
2 2 2 2
Risolviamo dunque il sistema delle due
equazioni e mostriamone il risultato senza i
passaggi passaggi algebrici di routine omettendone
i banali passaggi algebrici dei quali il lettore
può svolgere come esercizio:
⎧
⎪
⎪
⎨
⎪
⎪
⎪⎩
8 − y
1 = −
1
− 7 − x
1
2
⎧ x1
= 13
a ⎨ a
P
8 + y
1
− 7 + x y
1
1 = − 2
= 2 + 3 ⎩
2 2
In figura l'illustrazione grafica dell'esempio.
14
1
( 13, − 2)

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
Per quanto riguarda le generali espressioni
analitiche della legge di simmetria rispetto ad un
asse qualsiasi, si può dimostrare, imponendo le
due condizioni viste dall'esempio riportato sopra,
che le coordinate del punto simmetrico di una dato
punto rispetto ad retta di equazione " y=mx+q ",
vengono date dalle seguenti espressioni:
Punti simmetrici rispetto ad una retta di
equazione " y = mx + q " : P x, y P
1
x
1
, y
1
x
1
=
1 −
1 +
m2 x −
m2 2
y −
1 + m2 2m
q
1 + m2
2 1 2
y
2
1
=
m
x −
− m
y + q
1 + m2 1 + m2 1 + m2
Applichiamo ora la simmetria assiale rispetto
all' asse di equazione "y=2x-3" alla retta di
equazione y=x+1, sostituendo dapprima i valori
del coefficiente angolare e del termine noto nelle
espressioni generali e poi sostituendo:
y = x +
1 :
7x − y − 23 = 0
15
( ) a ( )
x
3 4 12
1
= − x + y +
5 5 5
a
y
4 3 6
1
= x + y −
5 5 5
4
x +
3
y −
6
= −
3
x +
4
y +
12
+ 1 a
5 5 5 5 5 5
4x + 3y − 6 = − 3x + 4y + 12 + 5 a
a
y = 7x − 23

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
FORMA MATRICIALE DELLA SIMMETRIA ASSIALE
Le coordinate del punto simmetrico di un dato
punto possono essere considerate come le
componenti di un vettore che risulta a seguito di
una applicazione dell'operatore di moltiplicazione
fra una matrice quadrata di dimensione 2 ed il
vettore di componenti le coordinate del punto
soggetto alla trasformazione di simmetria assiale:
⎡ 1 m2 2m
⎤
⎢ −
⎥
⎢ 1 m2 1 m2
⎥
x
⎡ x ⎤
+ +
uur ⎡ ⎤ uuur 1
⎢ ⎥
⎢ ⎥ uur v uv
V ⎢ ⎥ a V
1
A V+ B : A= ⎢ ⎥ ; B
y ⎢ y ⎥ = •
⎢ ⎥ ⎢ ⎥
⎢⎣ ⎥⎦
⎢
⎣ 1 ⎥
⎦
⎢
2m 1 2 ⎥
⎢ -
− m ⎥
⎢
1 m2 1 m2
⎥
+ +
⎣ ⎦
Rimanendo nei limiti imposti alla presente esposizione
non approfondiamo ulteriormente l'argomento che rimandando
ad altra trattazione, ma ci limitiamo a notare come il
determinante della matricie sia di valore (-1), consentendo
di interpretare la simmetria assiale come una operazione
composta da una rotazione ed una traslazione di un certo
angolo (alfa) rispetto rispetto all'asse orizzontale:
α
2
=m a Cos
1 2
( α ) =
− m
, Sin
m
2
( α ) =
2 1 + m 1 + m2
Cos ( α ) Sin ( α )
16
=
⎡ 2m
⋅ q ⎤
⎢
− 2
1 + m ⎥
⎢ ⎥
⎢ ⎥
⎢ 2q
⎥
⎢ 2
1 + m
⎥
⎣ ⎦
Det ( A ) =
1 −
1 +
m2 ⎛
⋅ ⎜ −
1 −
m2 ⎜
⎝ 1 +
m2 ⎞
⎟ −
2m ⋅
2m
=
m2 ⎟ 1 2 1 2
⎠ + m + m
=
2
2
− ⎛1 m ⎞ 4m2 ⎜ − ⎟ −
⎝ ⎠ =
2
2
⎛ 1 + m ⎞
− 1 + 2m2 − m4 − 4m2
=
2
2
⎛ 1 + m ⎞
2
2
− ⎛1 m ⎞
⎜ + ⎟
⎝ ⎠ =
2
2
⎛ 1 + m ⎞
− 1
Tg
a
⎛ ⎞
⎜ ⎟
⎝ ⎠
A=
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣⎢
Sin ( α ) − Cos ( α ) ⎥⎦

I. Savoia – Simmetrie nel piano cartesiano - Marzo 2011
SIMMETRIE NEL PIANO CARTESIANO
INDICE
SIMMETRIA RISPETTO AGLI ASSI CARTESIANI 1
SIMMETRIA CENTRALE RISPETTO ALL'ORIGINE 1
FUNZIONI SIMMETRICHE E LORO GRAFICI 2
SIMMETRIA DELLE FUNZIONI: PARITA' E DISPARITA' 5
FUNZIONI MATEMATICHE E SIMMETRIE 6
SIMMETRIA RISPETTO A RETTE PARALLELE AGLI ASSI: 10
SIMMETRIA RISPETTO ALLE BISETTRICI 11
SIMMETRIA RISPETTO AD ASSE OBLIQUO 13
FORMA MATRICIALE DELLA SIMMETRIA ASSIALE 15
INDICE 17
17