Distribuzione gaussiana di media μ e scarto quadratico medio σ ...
Distribuzione gaussiana di media μ e scarto quadratico medio σ ...
Distribuzione gaussiana di media μ e scarto quadratico medio σ ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>Distribuzione</strong> <strong>gaussiana</strong> <strong>di</strong> me<strong>di</strong>a <strong>μ</strong> e <strong>scarto</strong> <strong>quadratico</strong> me<strong>di</strong>o <strong>σ</strong> :<br />
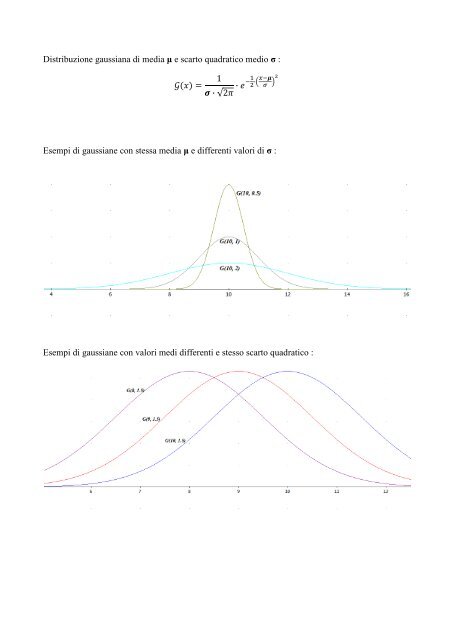
Esempi <strong>di</strong> gaussiane con stessa me<strong>di</strong>a <strong>μ</strong> e <strong>di</strong>fferenti valori <strong>di</strong> <strong>σ</strong> :<br />
Esempi <strong>di</strong> gaussiane con valori me<strong>di</strong> <strong>di</strong>fferenti e stesso <strong>scarto</strong> <strong>quadratico</strong> :
L’asse <strong>di</strong> simmetria delle Gaussiane è la retta x = <strong>μ</strong>, ma con una semplice “traslazione +<br />
<strong>di</strong>latazione” è possibile centrarle in 0 :<br />
Successivamente operiamo un’altra <strong>di</strong>latazione in modo che il valore massimo risulti<br />
moltiplicare per <strong>σ</strong>), alla fine la <strong>di</strong>stribuzione <strong>gaussiana</strong> avrà espressione :<br />
E assumerà la forma :<br />
(basterà<br />
Questa procedura si chiama standar<strong>di</strong>zzazione e rende possibile ricavare informazioni da un’unica<br />
curva, per l’appunto chiamata <strong>gaussiana</strong> standard , qualunque sia la <strong>gaussiana</strong> dalla quale partiamo.<br />
Di questa funzione è possibile leggere l’area sottesa su apposite tabelle : ne esistono<br />
sostanzialmente <strong>di</strong> due tipi :<br />
A) Quelle che forniscono l’area sottesa da - ∞ a z (con z > 0)
B) Quelle che forniscono l’area sottesa da 0 a z (con z > 0 )<br />
In ogni caso sarà comunque possibile determinare le aree delle parti complementari .<br />
Esempio 1<br />
Calcolare la probabilità che la variabile casuale standard z assuma valori compresi tra 1.52 e<br />
2.04, cioè che valga 1.52 ≤ z < 2.04 :<br />
leggiamo dalla tabella tipo-B ⇝ F(2.04) = 0.4793 :<br />
Leggiamo dalla tabella tipo-B ⇝ F(1.52) = 0.4357 :
E quin<strong>di</strong> l’area compresa tra i due valori sarà la <strong>di</strong>fferenza tra i due :<br />
F(2.04) – F(1.52) = 0.0436<br />
Cioè :<br />
Esercizio 1<br />
Il forno Palmisano confeziona il dolce Bussolà in pezzi da 0.5 kg. Il proprietario ha deciso<br />
<strong>di</strong> eseguire un’indagine statistica sulla sua produzione ed ha rilevato i seguenti dati : massa<br />
me<strong>di</strong>a della confezione <strong>μ</strong> = 0.506 Kg, <strong>scarto</strong> <strong>quadratico</strong> me<strong>di</strong>o <strong>σ</strong> = 0.009 kg.<br />
Per legge sulla confezione dev’essere riportata la massa netta pari a 0.500 Kg e la massa<br />
effettiva non può risultare minore <strong>di</strong> 0.495 kg.<br />
Quante sono le confezioni <strong>di</strong> Bussolà ven<strong>di</strong>bili ?<br />
Risol.<br />
1.- dobbiamo stimare la probabilità che sia x > 0.495, se x in<strong>di</strong>ca la massa netta
2.- “standar<strong>di</strong>zzare” il valore x = 0.495 :<br />
3.- ora possiamo operare con la <strong>gaussiana</strong> standard :<br />
4.- se usiamo la tabella tipo-A è sufficiente leggere F(1.22) = 0.8888<br />
infatti per la simmetria della figura :<br />
Le due aree sono uguali e la seconda la desumiamo dalla tabella tipo-A.
4bis.- se usiamo la tabella tipo-B dovremo eseguire qualche conto in più :<br />
dalla tabella ricaviamo F(1.22) = 0.3888<br />
E sfruttando il fatto che la metà <strong>di</strong> sinistra vale 0.5 :<br />
Avremo in totale 0.5 + 0.3888 = 0.8888 e per la simmetria :<br />
In ogni caso :