DERIVADAS TOTAIS E PARCIAIS Def. 1: Seja w = f(P) = f ... - PUCPR

DERIVADAS TOTAIS E PARCIAIS
Def. 1: Seja w = f(P) = f(x1,x2, ... ,xn) uma função de n variáveis. Chama-se acréscimo total
de w = f(P) no ponto P0 ao número real:
∆w= f ( P) − f ( P ) = f ( x + ∆x , x + ∆x , K, x + ∆x
) − f ( x , x , K , x ) .
0 1 1 2 2 n n 1 2 n
Vamos considerar os seguintes casos:
1 0 CASO: Para as funções de uma única variável x, isto é, y = f ( x)
, temos que P = x,
P0 = x0 e ∆y = f ( x)−
f(x0) = f ( x0 + ∆ x) − f ( x0)
.
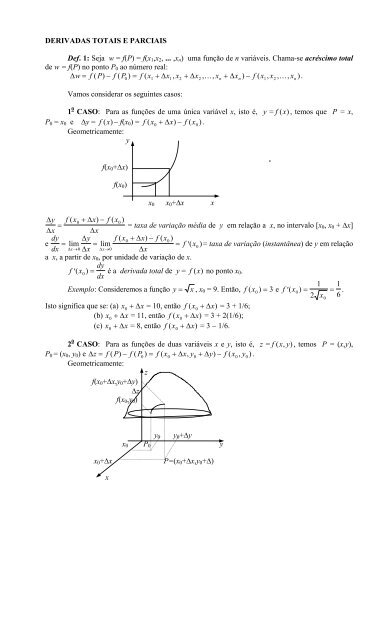
Geometricamente:
y
f(x0+∆x)
f(x0)
x0 x0+∆x x
∆y
f ( x0 + ∆x)
− f ( x0)
=
= taxa de variação média de y em relação a x, no intervalo [x0, x0 + ∆x]
∆x
∆x
e dy ∆y
f ( x0 + ∆x)
− f ( x0)
= lim = lim = f ′ ( x0
) = taxa de variação (instantânea) de y em relação
dx ∆x→0∆x∆x→0 ∆x
a x, a partir de x0, por unidade de variação de x.
dy
f ′ ( x0
) = é a derivada total de y = f ( x)
no ponto x0.
dx
1 1
Exemplo: Consideremos a função y = x,
x0 = 9. Então, f ( x0)
= 3 e f ′ ( x0)
= =
2 x 6 0
.
Isto significa que se: (a) x0 +∆ x = 10, então f ( x0 +∆ x)
= 3 + 1/6;
(b) x0 +∆ x = 11, então f ( x0 +∆ x)
= 3 + 2(1/6);
(c) x0 +∆ x = 8, então f ( x0 +∆ x)
= 3 − 1/6.
2 0 CASO: Para as funções de duas variáveis x e y, isto é, z = f ( x, y),
temos P = (x,y),
P0 = (x0, y0) e ∆z = f ( P) − f ( P0) = f ( x0 + ∆x, y0 + ∆y)
− f ( x0, y0
) .
Geometricamente:
z
f(x0+∆x,y0+∆y)
∆z
f(x0,y0)
y0 y0+∆y
x0 P0 y
x0+∆x P=(x0+∆x,y0+∆)
x

Neste caso, ∆z depende das variações de ∆x e de ∆y. Vamos considerar, então, que ∆z de-
⎯→ ⎯
pende da distância do ponto P0 ao ponto P, d(P0,P), que representa o módulo do vetor P0 P
P−P0 . Portanto, por analogia, temos que:
∆z
= taxa de variação média de z em relação às variações de x e y ou que, é a taxa de
d( P0P) variação média de z em relação à variação da distância entre P0 e P e, que,
dz
∆z
= lim = lim
d( P P)
d( P P)
P→P P P
0 0 →
0
0
f ( P) − f ( P0)
= lim
P−P ∆x ∆y
→
0
( , ) ( 00 , )
f ( x0 + ∆x, y0 + ∆y)
− f ( x0, y0)
2 2
∆x + ∆y
é a taxa de variação (instantânea) de z em relação a x e a y, a partir do ponto P0, por unidade de
distância de P0 a P. É, por analogia, chamada de derivada total de z = f(P) no ponto P0 e, em relação
a x e a y.
Exemplo: Calcular a derivada total de z = f ( x, y)=
3x 2 y, no ponto P0 = (1,2).
2 2
dz f ( 1+ ∆x, 2+ ∆y)
− f ( 12 , ) 3( 1+ ∆x) ( 2+ ∆y)
−3(
1) 2
= lim = lim ou,
d( P P)
∆x→
0
2 2 ∆x→
0
2 2
0
∆x + ∆y
∆x + ∆y
∆y→
0
∆y→
0
2 2
2 2
dz 6+ 12∆x+ 3∆y++ 6∆x + 3∆x ∆y−6
12∆x+ 3∆y+ 6∆x + 3∆x
∆y
= lim
= lim
d( P0P) ∆x→
0
2 2
∆x→
0
2 2
∆x + ∆y
∆x + ∆y
∆y→
0
Como o limite apresenta a indeterminação 0
e não apresenta simplificação, vamos usar os
0
2
⎧∆x
→ 0 12∆x+ 6∆x ∆x( 12 + 6∆x)
caminhos: C ⎨ 1 ⇒ lim = lim = 12 e
∆y
= 0 ∆x
0
2 ⎩
→
∆x→
0
∆x
∆x
∆y=
0
⎧ ∆x
= 0 3∆y
C ⎨ 2 ⇒ lim = 3
⎩∆y
→ 0 ∆x=
0 ∆y
∆y→
0
Como os resultados são diferentes, não existe o limite. Isto é, esta função não tem derivada
total no ponto (1,2).
Obs.: Em geral, z = f ( x, y)
não tem derivada total. Mas, em particular, vamos considerar os resultados
dos limites por caminhos, isto é, as derivadas por caminhos ou, as derivadas parciais, definidas
por:
Def. 2: Chama-se derivada parcial de z = f ( x, y)
no ponto P0 = (x0,y0) e, em relação a x, ao
número real fx ( x0, y0
) , definido por
f ( x0 + ∆x,
y0) − f ( x0, y0)
∂z
fx( x0, y0)
= lim = ( x0, y0)
∆x→
0 ∆x
∂x
desde que o limite exista.
Obs.: Usamos a letra d para indicar a derivada total. Para não confundir, usamos a letra d do alfabeto
Ronde, ∂ , para indicar a derivada parcial.
Analogamente, podemos ter a derivada parcial em relação a y, isto é:
∆y→
0
=

Def. 3: Chama-se derivada parcial de z = f ( x, y)
no ponto P0 = (x0,y0) e, em relação a y, ao
número real f y ( x0, y0
) , definido por
f ( x0, y0 + ∆y)
− f ( x0, y0)
∂z
f y ( x0, y0)
= lim = ( x0, y0)
∆y→
0 ∆y
∂y
desde que o limite exista.
Exemplos:
1) Determine as derivadas parciais de z = f ( x, y)
= 3x 2 y no ponto (1,2) e, em relação a x e,
em relação a y.
Solução:
(a) Em relação a x:
2 2
2
f ( 1+ ∆x,
2) − f ( 12 , ) 3( 1+ ∆x)
2−3( 1) 2
6+ 12∆x+ 6∆x −6
f x (,) 12 = lim = lim = f x (,) 12 = lim
∆x→0 ∆x
∆x→0
∆x
∆x→
0 ∆x
( 12 + 6∆x)
∆x
f x (,) 12 = lim = 12.
∆x→
0 ∆x
f
y
(b) Em relação a y:
2 2
f (, 12+ ∆y)
− f (,) 12 31 () ( 2+ ∆y)
−31
() 2 6+ 3∆y− 6 3∆y
(,) 12 = lim = lim = lim = lim = 3.
∆y→0 ∆y
∆y→0
∆y
∆y→0 ∆y
∆y→0
∆y
2) Idem (1) para P0 = (x0,y0) genérico.
Solução:
(a) Em relação a x:
2
2
f ( x0 + ∆x,
y0) − f ( x0, y0)
3( x0+ ∆x)
y0 −3x0y0
fx( x0, y0)
= lim = lim ∴
∆x→
0 ∆x
∆x→
0 ∆x
2
3 2
3x0y0 + 6x0y0∆x+ 3y0∆x −3x0y0(
6xy 0 0 + 3y0∆x)
∆x
fx ( x0, y0
) = lim
= lim
∆x→
0
∆x
∆x→
0 ∆x
f ( x , y ) = 6x
y .
x
0 0 0 0
(b) Em relação a y:
2
2
f ( x0, y0 + ∆y)
− f ( x0, y0)
3x0( y0 + ∆y)
−3x0y
f y ( x0, y0)
= lim = lim
∆y→
0 ∆y
∆y→
0 ∆y
2
f ( x , y ) = 3x
.
y
0 0 0
0
∴
2
3x0∆y
= lim
∆y→0
∆y
Se a função z = f ( x, y)
admite derivadas parciais em relação a x e a y em todos os pontos
P0 de uma região D do plano IR 2 , dizemos que z = f ( x, y)
é derivável parcialmente em relação a x
e a y em D. Neste caso, podemos definir as funções derivadas parciais em D. Isto é:
(i) ∂z
= fx( x, y)
= lim
∂x
∆x→
0
f ( x+ ∆x,
y) − f ( x, y)
∆x
(ii) ∂z
= f y ( x, y)
= lim
∂y
∆y→
0
f ( x, y+ ∆y)
− f ( x, y)
∆y
é a função derivada parcial de f ( x, y)
em D;
é a função derivada parcial de f ( x, y)
em D.
∴

Exemplo:
Vimos (ex. 2, anterior) que a função f ( x, y)
= 3x 2 y tem derivada parcial em relação a x e
em relação a y, em todos os pontos (x0,y0) do IR 2 . Logo, é derivável parcialmente em IR 2 e, suas
funções derivadas parciais ou apenas derivadas parciais são:
∂z
∂z
= f x ( x, y) = 6 xy e
= f y ( x, y) = 3x ∂x
∂y
2 .
CÁLCULO DAS DERIVADAS PARCIAIS DE z = f(x,y)
Para calcularmos as derivadas parciais de z = f ( x, y)
não precisamos calcular os limites que
as definem. Podemos usar as fórmulas de derivação usadas para o calculo das derivadas de
y = f ( x).
(a) Derivada parcial em relação a x:
Para calcularmos as derivadas parciais em relação a x, vamos usar a função auxiliar
ϕ (x) = f ( x, y0
) em que consideramos y = y0 constante. Então:
∂z
⎛∂z
⎞
f ( x+ ∆x,
y0) − f ( x, y0)
ϕ( x+ ∆x)
−ϕ(
x)
= ⎜ ⎟ = fx( x, y0)
= lim = lim = ϕ′
( x)
.
∂x
⎝∂x
⎠
∆x→0∆x∆x→0∆x y= y
0
Exemplos:
1) Calcular a derivada parcial em relação a x de z = f ( x, y)
= 3x 2 y.
Sol.: Considerando y = y0 = b (constante), temos a função auxiliar ϕ (x) = f ( x, b)
= 3x 2 b.
Derivando ϕ em relação a x, obtemos ϕ‘(x) = 6xb. Como ∂ ⎛ z ⎞
⎜ ⎟ =6 xb = ϕ‘(x), voltamos com o
⎝∂x
⎠y=
b
valor b = y obtendo ∂z
= 6 xy que é a derivada de f ( x, y)
em relação a x.
∂x
2) Calcular a derivada parcial de z = f ( x, y)
= x 2 + y 2 + 3xy 2 + 5x − y + 10 em relação a x.
Sol.: Para y = y0 = b (constante), a função auxiliar é ϕ (x) = x 2 + b 2 + 3xb 2 + 5x − b + 10.
Derivando em relação a x obtemos ϕ‘(x) = 2x + 3b 2 + 5. Voltando com b = y, temos que,
∂z
2
= fx( x, y) = 2x+ 3y + 5.
∂x
(b) Derivada parcial em relação a y:
De modo análogo, vamos usar a função auxiliar ψ(y) = f ( x0 , y)
em que consideramos
x = x0 constante. Então:
∂z
⎛∂z
⎞
f ( x0, y+ ∆y)
− f ( x0, y)
ψ( y+ ∆y)
−ψ(
y)
= ⎜ ⎟ = f y ( x0, y)
= lim = lim = ψ ′ ( y)
.
∂y
⎝∂y
⎠
∆y→0∆y∆y→0∆y x= x
0
Exemplos:
1) Calcular a derivada parcial em relação a y de z = f ( x, y)
= 3x 2 y.
Sol.: Considerando x = x0 = a (constante), temos a função auxiliar ψ (y) = f ( a, y)
= 3a 2 y.
Derivando ψ em relação a y, obtemos ψ ‘(y) = 3a 2 . Como ∂ ⎛ z ⎞
⎜ ⎟ =3a ⎝∂y
⎠x=
a
2 = ψ ‘(y), voltamos com o
valor a = x obtendo ∂z
=3x ∂y
2 que é a derivada de f ( x, y)
em relação a y.

2) Calcular a derivada parcial de z = f ( x, y)
= x 2 + y 2 + 3xy 2 + 5x − y + 10 em relação a x.
Sol.: Para x = x0 = a (constante), a função auxiliar é ψ (y) = a 2 + y 2 + 3ay 2 + 5a − y + 10.
Derivando em relação a y obtemos ψ ‘(y) = 2y + 6ay −1. Voltando com a = x, temos que,
∂z
= fy( x, y) = 2y+ 6xy− 1.
∂y
3 0 CASO: Para as funções do tipo w = f ( x, y, z),
de três variáveis, temos que P = (x,y,z),
P0 = (x0,y0,z0) e ∆w = f(P) − f(P0) = f(x0 + ∆x, y0 + ∆y, z0 + ∆z) − f(x0,y0,z0).
Neste caso, não temos representação geométrica e, por analogia, concluímos que não existe a
derivada total de w = f ( x, y, z)
em relação conjunta às três variáveis x, y e z. Mas, existem as derivadas
parciais, isto é:
Def. 4: Dada a função w = f ( x, y, z)
das três variáveis x, y, z e, o ponto P0 = (x0,y0,z0), então,
temos que a derivada parcial de w = f(x,y,z), no ponto P0 e,
(i) em relação a x, é dada por
∂w
f ( x0 + ∆x,
y0, z0) − f ( x0, y0, z0)
= fx( x0, y0, z0)
= lim ;
∂x
∆x→
0
∆x
(ii) em relação a y, é dada por
∂w
f ( x0, y0+ ∆y,
z0) − f ( x0, y0, z0)
= fy( x0, y0, z0)
= lim ;
∂y
∆y→
0
∆y
(iii) em relação a z, é dada por
∂w
f ( x0, y0, z0+ ∆z)
− f ( x0, y0, z0)
= fz( x0, y0, z0)
= lim ,
∂z
∆z→0
∆z
desde que os limites existam.
Se as derivadas parciais de w = f ( x, y, z)
existem em todos os pontos P = (x0,y0,z0) de uma
região R do IR 3 , dizemos que w = f ( x, y, z)
é derivável parcialmente em R e, podemos calcular
suas funções derivadas parciais em relação a x, y e z. (Basta trocar na definição 4, x0 por x, y0 por
y, z0 por z e, calcular os limites).
Exemplo:
Calcular as derivadas parciais em relação a x, y e z da função w = f ( x, y, z)
= x 3 y 2 z − 5xy +
3yz − 2xz + 10.
Sol.: (a) Em relação a x:
∂w
f( x+ ∆xyz
, , ) − f( xyz , , )
=lim
∂x
∆x→
0 ∆x
3 2 3 2
∂w
( x+ ∆x) y z− 5( x+ ∆x) y+ 3yz− 2( x+ ∆x)
z+ 10− x y z+ 5xy− 3yz+ 2xz−10 = lim
∂x
∆x→
0
∆x
2 2 2 2 2 3
∂w
3x y z∆x+ 3x z∆x + y z∆x −5y∆x−2z∆x =lim
= 3x
∂x
∆x→0
∆x
2 y 2 z − 5y − 2z.
(b) Em relação a y:
∂w
f ( x, y+ ∆y,
z) − f ( x, y, z)
=lim
∂y
∆y→
0 ∆y
3 2 3 2
∂w
x ( y+ ∆y) z− 5x( y+ ∆y) + 3( y+ ∆y)
z− 2xz+ 10− x y z+ 5xy− 3yz+ 2xz−10 = lim
∂y
∆y→
0
∆y
3
∂w
2x yz− 5x∆y+ 3z∆y
3
= lim
= 2x yz− 5x+ 3z.
∂y
∆y→
0 ∆y

(c) Em relação a z:
∂w
f ( x, y, z+ ∆z)
− f ( x, y, z)
=lim
∂z
∆z→0
∆z
3 2 3 2
∂w
x y ( z+ ∆z) − 5xy+ 3y( z+ ∆z) − 2x( z+ ∆z)
+ 10− x y z+ 5xy− 3yz+ 2xz−10 = lim
∂z
∆z→0
∆z
3 2
∂w
x y ∆z+ 3y∆z−2x∆z 3 2
= = x y + 3y− 2x.
∂z
∆z
CÁLCULO DAS DERIVADAS PARCIAIS DE w = f(x,y,z)
De modo análogo ao caso anterior, vamos calcular as derivadas parciais de w = f ( x, y, z)
em
relação as variáveis x, y e z, usando funções auxiliares que são funções de uma única variável. Isto
é, as duas outras variáveis são consideradas como constantes.
(a) Derivação parcial em relação a x:
Vamos considerar a função auxiliar ϕ(x) = f ( x, y0, z0
) em que y = y0 e z = z0 são constantes.
Então:
∂w
∂w
f x x y z f x y z ϕ x x ϕ x
= ϕ x
∂x
∂x
y y x x
x x
⎛ ⎞ ( + ∆ , 0, 0) − ( , 0, 0)
( + ∆ ) − ( )
⎜ ⎟ = lim = lim = ′ ( ) .
⎝ ⎠ = 0 ∆ →0∆∆ →0∆
z= z
0
(b) Derivação parcial em relação a y:
Vamos considerar a função auxiliar ψ(y) = f ( x0, y, z0
) em que x = x0 e z = z0 são constantes.
Então:
∂w
∂w
f x y y z f x y z ψ y y ψ y
= ψ y
∂y
∂y
x x y y
y y
⎛ ⎞ ( 0, + ∆ , 0) − ( 0, , 0)
( + ∆ ) − ( )
⎜ ⎟ = lim = lim = ′ ( ) .
⎝ ⎠ = 0 ∆ →0∆∆ →0∆
z= z
0
(c) Derivação parcial em relação a z:
Vamos considerar a função auxiliar λ(y) = f ( x0, y0 , z)
em que x = x0 e y = y0 são constantes.
Então:
∂w
∂w
f x y z z f x y z λ z z λ z
. = λ z
∂z
∂z
x x x z
z z
⎛ ⎞ ( 0, 0, + ∆ ) − ( 0, 0,
) ( + ∆ ) − ( )
⎜ ⎟ = lim = lim = ′ () .
⎝ ⎠ = 0 ∆ →0∆∆ →0∆
y= y
0
Exemplos:
1) Calcular as derivadas parciais de w = f ( x, y, z)
= x 3 y 2 z − 5xy + 3yz − 2xz + 10, em relação
a x, y e z.
Sol.: (a) Em relação a x:
Fazendo y = y0 = b e z = z0 = c, constantes, temos que ϕ(x) = f(x,b,c) = x 3 b 2 c − 5xb + 3bc −
2xc + 10. Derivando em relação a x, ϕ‘(x) = 3x 2 b 2 c − 5b − 2c. Voltando com os valores de b = y, c
= z, obtemos ∂w
2 2
= fx( x, y, z) = 3x y z−5y−2z. ∂x
(b) Em relação a y:
Para x = x0 = a e z = z0 = c, constantes, ψ(y) = f(a,y,c) = a 3 y 2 c − 5ay + 3yc − 2ac + 10.
Derivando em relação a y, obtemos ψ‘(y) = 2a 3 yc − 5a + 3c. Voltando com a = x e c = z, resulta
que ∂w
3
= f y ( x, y, z) = 2x yz− 5x+ 3z.
∂y

(c) Em relação a z:
Considerando x = x0 = a e y = y0 = b, resulta que λ(z) = f(a,b,z) = a 3 b 2 z − 5ab + 3bz − 2az
+ 10. Derivando em relação a z, obtemos λ‘(z) = a 3 b 2 + 3b − 2a. Voltando com os valores de a =
x, b = y, resulta ∂w
3 2
= fz( x, y, z) = x y + 3y−2 x.
∂z
4 0 CASO: GENERALIZAÇÃO
Dada a função de n variáveis w = f(x1,x2, . . . ,xn) então, suas derivadas parciais em relação d
cada uma das n variáveis é dada por:
(a) ∂w
f ( x1 + ∆x1,
x2, K, xn) − f ( x1, x2, K , xn)
= lim ;
∂x
∆x1
→0
1
∆x1
(b) ∂w
f ( x1, x2 + ∆x2,
K, xn) − f ( x1, x2, K , xn)
= lim ;
∂x
∆x2
→0
∆x
2
M
(n) ∂w
= lim
∂x
∆xn
→0
n
f ( x1, x2, K, xn + ∆xn)
− f ( x1, x2, K , xn)
,
∆xn
desde que os limites existam.
2
As derivadas parciais podem ser calculadas diretamente se considerarmos as outras variáveis
como constantes.
EXERCÍCIOS RESOLVIDOS:
1) Calcular as funções derivadas parciais de z = f ( x, y)
=
lar fx (2,1) e fy(2,1).
Sol.:
(a) Em relação a x:
2 2
9 − x − y . Em seguida, calcu-
2 2
Para y = b, temos que ϕ (x) = f(x,b) = 9 − x −b
. Derivando em relação a x, obtemos:
− 2x
ϕ‘(x) =
2 2
2 9−
x −b
. Voltando com y = b, temos que fx(x,y) =
−x
2 2
9 − x − y
e fx (2,1) = −1;
(b) Em relação a y:
2 2
Considerando x = a, temos que ψ(y) = f(a,y) = 9 −a − y . Derivando em relação a y,
− 2y
obtemos ψ‘(y) =
2 2
2 9−a
− y . Voltando com x = a, temos que fy(x,y)
fy(2,1) = − ½ .
=
− y
e que
2 2
9 − x − y
2) Calcular as derivadas parciais de z = ln(x 2 + xy + y 2 )
Sol.:
(a) Em relação a x:
Fazendo y = b, resulta que ϕ(x) = ln(x 2 + xb + b 2 2x+
b
) cuja derivada é ϕ‘(x) =
x + xb+ b
Como b = y, temos que ∂z
2x+
y
= 2 2
∂x
x + xy+ y
;
2 2
.

(b) Em relação a y:
Para x = a, ψ(y) = ln(a 2 + ay + y 2 a+ 2y
) e sua derivada é ψ‘(y) =
a + ay+ y
por x, obtemos ∂z
x+ 2y
= 2 2
∂y
x + xy+ y
.
3) Calcular ∂z
∂z
2xy
e para z = 2 2
∂x
∂y
x + y
.
Sol.:
(a) Cálculo de ∂z
∂x
:
Para y = b, ϕ(x) = 2 2 2
xb
2bx ( + y) −2bx(
2x)
2 2 e ϕ‘(x) = 2 2 2 =
x + b
( x + b )
2 2
b = y, temos que ∂
3
z 2y − 2xy
= 2 2 2 .
∂x
( x + y )
(b) Em relação a y:
Fazendo x = a, ψ(y) = 2
2 2
ay
2ax ( + y) −2ay(
2y)
2 2 e ψ‘(y) = 2 2 2 =
a + y
( x + y )
2 2
como a = x, temos que ∂
3
z 2x − 2xy
= 2 2 2 .
∂y
( x + y )
4) Determine as derivadas parciais de z
Sol.:
(a) Em relação a x:
ϕ(x) = f(x,b) = arctg b
. Derivando, ϕ‘(x) =
x
Portanto, ∂z
− y
=
∂x
x + y
2 2 .
y
= arctg .
x
−
+ ⎛
b
2
x
b ⎞
1 ⎜ ⎟
⎝ x ⎠
2
2 2
by − bx
( x + b )
2
2 2 2
( a
−
+ y )
2 2
ax ay
2 2 2
. Substituindo a
. Logo, como
. Logo,
b
− 2
2
x bx −b
= 2 2 = − 2 2 2 = 2 2 .
x + b x ( x + y ) x + y
2
x
(b) Em relação a y:
ψ(y) = f(a,y) = arctg y
1 1
. Derivando, ψ‘(y) =
a a
2 2 2
a y a y
1+
2
a a
⎛
2
a
= = 2 2 . Simplificando
⎞ + aa ( + y )
⎜ ⎟
⎝ ⎠
por a, e substituindo a por x, obtemos ∂z
∂y
=
x
2 2 .
x + y
y 5) Se z = tg x,
determine suas derivadas parciais.
Sol.:
(a) Em relação a x:
ϕ(x) = f(x,b) = b tgx . Derivando, ϕ‘(x) =
sec 2
x
b x b
b tg
( )
−1
. Para b = y, temos ∂z
∂x
=
sec 2
x
1
y x y y − .
( tg )

(b) Em relação a y:
y ψ(y) = f(a,y) = tga . Para derivarmos, vamos escrever na forma ψ(y) = f(a,y) =
1
y a = ( tga)y
tg . Derivando em relação a y, obtemos ψ‘(y) = ( a) y ln tga
y
∂z
tgx
= − 2 ln tgx
.
∂y
y
⎛ 1 ⎞
⎜
⎜−
y
⎟ . Para a = x, temos
⎝ ⎠
1
tg 2
6) Determine as derivadas parciais de w = xy 2 z 3 − 5xy + 3yz.
Sol.: A função w é uma função das três variáveis x, y e z. Devemos então calcular as três derivadas
parciais. Isto é:
(a) Em relação a x:
Considerando y = b e z = c, constantes, obtemos a função auxiliar ϕ(x) = f(x,b,c) = xb 2 c 3
− 5xb + 3bc. Derivando em relação a x obtemos ϕ‘(x) = b 2 c 3 − 5b. Voltando com o b = y e c = z,
obtemos ∂w
∂x
= y2z 3 − 5y.
(b) Em relação a y:
Para x = a e z = c, temos que ψ(y) = f(a,y,c) = ay 2 c 3 − 5ac + 3yc. Derivando, ψ‘(y) =
2ayc 3 + 3c.
Voltando com os valores de a = x e c = z, obtemos ∂w
∂y
= 2xyz3 + 3z.
(c) Em relação a z:
Considerando x = a e y = b, constantes, temos que λ(z) = f(a,b,z) = ab 2 z 3 − 5ab + 3bz.
Derivando em relação a z, obtemos λ‘(z) = 3ab 2 z 2 + 3b. Voltando com a = x e b = y, temos que
∂w
∂z
= 3xy2z 2 + 3y.
7) Calcule as derivadas parciais de w = xy z .
Sol.:
a) Em relação a x:
ϕ(x) = f(x,b,c) = xb c . Derivando, ϕ‘(x) = b c . Logo, ∂w
∂x
= yz .
(b) Em relação a y:
ψ(y) = f(a,y,c) = ay c . Derivando, ψ‘(y) = acy c -- 1 . Portanto, ∂w
∂
y = xzyz − 1 .
(c) Em relação a z:
λ(z) = f(a,b,z) = ab z . Derivando, λ‘(z) = ab z lnb. Logo, ∂w
∂z
= xyzlny. 8) Calcule as derivadas parciais de w x y z t
= + + + .
y z t u
Sol.: Aqui temos w = f(x,y,z,t,u). Vamos, então, calcular cinco derivadas parciais.
(a) Em relação a x:
ϕ(x) = f(x,b,c,d,e) = x b c d
+ + + . Derivando, ϕ‘(x) =
b c d e
1 ∂w
1
e =
b ∂x
y .

(b) Em relação a y:
ψ(y) = f(a,y,c,d,e) = a y c d
a
+ + + . Derivando, ψ‘(y) = − 2
y c d e
y
1 ∂w
x
+ . Logo, = − 2
c ∂y
y
1
+ .
z
(c) Em relação a z:
λ(z) = f(a,b,z,d,e) = a b z d
b 1 ∂w
y 1
+ + + . Derivando, λ‘(z) = − 2 + . Logo, = − 2 + .
b z d e
z d ∂z
z t
(d) Em relação a t:
θ(t) = f(a,b,c,t,e) = a b c t
c 1 ∂w
z 1
+ + + . Derivando, θ‘(t) = − 2 + . Logo, = − 2 + .
b c t e
t e ∂t
t u
(e) Em relação a u:
ρ(u) = f(a,b,c,d,u) = a
b
b c d
+ + + . Derivando, ρ‘(u) = −
c d u
d ∂w
2 . Logo,
u ∂u
t
= − 2 .
u
2 2
x + y
9) Mostre que se z = então, x
x−y ∂z
∂z
+ y = z.
∂x
∂y
Sol.: (a) ∂z
∂x
=
2 2
2 2
2xx ( − y) − ( x + y)(
1) x −2xy− y
2 = 2 ;
( x−y) ( x−y) (b) ∂
2 2
2 2
z 2yx ( − y) − ( x + y)(
− 1) x + 2xy−
y
= 2 = 2 .
∂y
( x−y) ( x−y) Substituindo na equação a derivadas parciais, obtemos:
x ∂
2 2
2 2
z ∂z
⎡ x −2xy− y ⎤ ⎡ x + 2xy−
y ⎤
+ y = x 2 y 2
∂x
∂y
⎢
⎣ x−y ⎥+ ⎢
⎦ ⎣ x−y ⎥ =
( ) ( ) ⎦
x x y xy x y xy y
−2 − + + 2 −
2
( x−y) x ∂
2 2
z ∂z
x ( x− y) + y ( x− y)
+ y = 2 =
∂x
∂y
( x−y) x y
2 2
+
= z.
#
x−y 3 2 2 2 2 3
∂x
∂x
∂ρ
10) Se x = ρcosθ e y = ρsenθ , determine
∂y
∂θ
∂y
∂ρ ∂θ
.
Sol.: Derivando parcialmente as funções x = f(ρ,θ) e y = f(ρ,θ), obtemos:
∂x
∂x
∂y
∂y
= cos θ , = − ρsen θ , = sen θ e = ρcos θ . Substituindo no determinante,
∂ρ ∂θ
∂ρ ∂θ
∂x
∂x
∂ρ
obtemos:
∂y
∂θ cosθ ∂y
=
senθ − ρsenθ ρcosθ 2
= ρcos θ
2
+ ρsen θ = ρ(cos
∂ρ ∂θ
2 θ + sen 2 θ ) = ρ.
EXERCÍCIOS PROPOSTOS
(I) Calcular as derivadas parciais de z = f(x,y) em relação a x e a y de:
1) f ( x, y)
= 2x − 7y 2 , no ponto (1,2) 2) f ( x, y)
= x 2 + 3xy − y 2 , no ponto (2,1)
3) f ( x, y)
= 1 − 3xy, no ponto (1,2) 4) f ( x, y)
= xy 2 − 3x 2 y 3 , no ponto (1, −1)
∴

x
5) f ( x, y) = xy+
, no ponto (2,1)
y
(II) Calcular as derivadas parciais das seguintes funções:
1) f ( x, y)
= 3x 2 − 2xy + 5y 4 + xy 2 − 4x + y + 7 2) f ( x, y)
= x 2 2 + xy + x y
5 2 7
3) f ( x, y)
= x y
1
4) f ( x, y)
=
3 3 2
x y
5) f ( x, y)
=
2 2
x − y
6) f ( x, y)
= x y−7 7) z = e x+y 8) z = x
y
9) z = x 2 cosy 10) z = 3cos(xy) + 5sen(xy)
x y
11) z =
x y
−
+ 12) z = xcosy + ysenx
13) z = ln
2 2
x + y
2
14) z = 1 − y
2xy
15) f ( x, y)
= 2 2
x + y
16) z = xy
y
17) z = arctg
x
18) z = ln(
x+ 2 2
x + y )
y
x 19) z = e
sen
20) z = arcsen
2 2
x − y
2 2
x + y
x + 1
21) z = lnsen
y
x y
e + e
22) z =
cos x+ sen y
3 2
y + xz
23) f ( x, y, z)
= 2 2 2
x + y + z
24) f ( x, y, z)
= ln(xy + z)
25) w = (xy) z 26) w =
x+ y+ z
2 2 2
x + y + z
27) w = z xy xyz xy
28) w= e +arctg
z
3 2
29) w= ln
2 2 2
x + y + z
30) f ( x, y, z, t) = arctg ( xyzt)
(III) Verificar as identidades ou calcular o valor de:
2
x
1) Se z = 2 2 , então, x
x + y
z
y
x
z ∂ ∂
+ = z
∂ ∂y
x
2) Se z = 2 2 , então, x
x + y
z
y
x
z ∂ ∂
+ =
∂ ∂y
y
x
3) Se z = xy+ xe , então, x z
y
x
z ∂ ∂
+ = xy + z
∂ ∂y
y
4) Se z = ln , então, x
x
z
y
x
z ∂ ∂
+ =
∂ ∂y
5) Se w = (x− y)(y− z)(z− x), então, ∂w
∂w
∂w
+ + =
∂x
∂y
∂z
x y
6) Se w= x+
x z
− ∂w
∂w
∂w
, então, + + =
− ∂x
∂y
∂z
1
1
3 2

DERIVADAS PARCIAIS SUCESSIVAS
Se a função w = f(P) admite derivadas parciais em relação a todas as variáveis independentes,
x1,x2, ..., xn e, estas funções derivadas parciais admitem derivadas parciais em relação a todas as
variáveis, então, suas derivadas parciais são chamadas de derivadas parciais de segunda ordem de
w = f(P).
Se as derivadas de segunda ordem são parcialmente deriváveis, suas derivadas são chamadas
de derivadas parciais de terceira ordem de w = f(P) e, assim, sucessivamente.
1) Para z = f(x, y), temos as seguintes derivadas sucessivas:
⎧ 3
∂ z
⎪ 3 = f xxx
∂x
⎪ 3
∂ z
⎪
2 = f xxy
⎪ ∂∂ yx
⎧ 2
3
∂ z ⎪ ∂ z
⎪ = f = f
2 xx ⎪
xyx
∂x
∂∂∂ xyx
⎪ 2 ⎪ 3
⎧∂z
∂ z z
= f
⎪ = f ⎪
∂
f
⎪ x
xy 2 = xyy
x yx yx
z = f x y ⎨
∂ ⎪∂∂
⎪ ∂ ∂
( , ) z
⎨ 2 ∂
⎨ 3
⎪
z z
= f ⎪
∂
y = f ⎪
∂
yx 2 = f yxx
⎩∂y
12 4 34 ⎪∂∂
xy ⎪ ∂ xy ∂
2
3
1a
ordem ⎪ ∂ z ⎪ ∂ z
⎪ 2 − f yy = f yxy
⎩ ∂y
⎪
∂∂∂ yxy
142443⎪3 2aordem
⎪
∂ z
2 = f yyx
⎪ ∂∂ x y
⎪ 3
∂ z
⎪ 3 = f yyy
⎩ ∂y
144244 3
3a
ordem
Obs.: O número de derivadas parciais é 2 n em que n é a ordem das derivadas.
Exemplo: Calcular as derivadas de 3 a ordem de z = f ( x, y)
= x 4 y 5 + 5x 3 y 3 − 4x 2 y − 5
Sol.:
Derivadas de primeira ordem
∂z
∂x
= 4x3y 5 + 15x 2 y 3 − 4xy 2 +3
∂z
∂y
= 5x4y 4 + 15x 3 y 2 − 4x 2 Derivadas de segunda ordem
y − 5
∂ z
∂x
2 = 12x2y 5 + 30xy 3 2
− 4y
2
∂ z
∂∂ xy = 20x3y 4 + 45x 2 y 2 − 8xy
2
∂ z
∂∂ yx = 20x3y 4 + 45x 2 y 2 − 8xy ∂
2
z
2
∂y
= 20x4y 3 + 30x 3 y − 4x 2
Derivadas de terceira ordem
∂
3
z
3
∂x
= 24xy5 3
+ 30y
3
∂ z
2
∂∂ yx = 60x2y 4 + 90xy 2 − 8y
∂
3
z
2
∂x ∂y
= 60x2y 4 + 90xy 2 − 8y ∂
3
z
∂∂∂ yxy = 80x3y 3 + 90x 2 y − 8x
3
∂ z
∂∂∂ xyx = 60x2y 4 + 90xy 2 − 8y ∂
3
z
2
∂y ∂x
= 80x3y 3 + 90x 2 y − 8x
∂
3
z
2
∂∂ xy = 80x3y 3 + 90x 2 y − 8x ∂
3
z
3
∂y
= 60x4y 2 + 30x 3

2) Para w = f(x, y, z), temos as seguintes derivadas parciais
⎧ 2
∂ w
⎪ 2 = f xx
∂x
⎪ 2
∂ w
⎪ = f xy
⎪∂∂
yx
2
⎪ ∂ w
⎪ = f xz
∂∂ zx
⎪ 2
⎧∂w
∂ w
= f
⎪ = f
⎪
yx
x
∂x
⎪∂∂
xy
⎪
2
∂w
⎪∂
w
w= f ( x, y, z)
⎨ = f ⎨ y 2 = f yy
⎪ ∂y
⎪ ∂y
2
⎪∂w
w
= f
⎪ ∂
z ⎩
= f
z ⎪
yz
12 4∂ 34 ∂∂ zy
aordem
⎪ 2
1 ∂ w
⎪ = f zx
⎪ ∂∂ xz
2
⎪ ∂ w
= f zy ⎪ ∂∂ yz
⎪ 2
∂ w
⎪ 2 = f zz ⎩
1∂4z244 3
2aordem
Obs.: O número de derivadas parciais é 3 n em que n é a ordem das derivadas.
Exemplo: Calcular as derivadas de segunda ordem de w = f ( x, y, z)
= x 3 y 4 z 5 + x 2 y 2 z 2 + 3xyz +
5x − 6y + 7z − 12.
Sol.:
Derivadas de primeira ordem
∂w
∂x
= 3x2y 4 z 5 + 2xy 2 z 2 + 3yz + 5 ∂w
∂y
= 4x3y 3 z 5 + 2x 2 yz 2 + 3xz − 6 ∂w
∂z
= 5x3y 4 z 4 + 2x 2 y 2 3xy + 7
z +
Derivadas de segunda ordem
2
∂ w
2
∂x
= 6xy4z 5 + 2y 2 2
z
2
∂ w
∂∂ yx = 12x2y 3 z 5 + 4xyz 2 + 3z ∂
2
w
∂∂ zx = 15x2y 4 z 4 + 4xy 2 3y
z +
2
∂ w
∂∂ xy = 12x2y 3 z 5 + 4xyz 2 + 3z
2
∂ w
2
∂y
= 12x3y 2 z 5 + 2x 2 2
z
2
∂ w
∂∂ zy = 20x3y 3 z 4 + 4x 2 3x
yz +
2
∂ w
∂∂ xz = 15x2y 4 z 4 + 4xy 2 z + 3y
2
∂ w
∂∂ yz = 20x3y 3 z 4 + 4x 2 yz + 3x ∂
2
w
2 = 20x
∂z
3 y 4 z 4 + 2x 2 y 2
Teorema 1: Se a função w = f(P) admite derivadas parciais mistas de ordem n, contínuas em
uma região R do IR n , então, suas derivadas parciais mistas são iguais.

INTERPRETAÇÃO DAS DERIVADAS PARCIAIS
1) DA FUNÇÃO z = f(x,y)
1.1) GEOMÉTRICA
Para calcularmos as derivadas parciais de z = f ( x, y)
, usamos as funções auxiliares
ϕ(x) = f(x,y0) e ψ(y) = f(x0,y) nas quais, y0 e x0 são, respectivamente, constantes.
(a) Em relação a x:
A função ϕ(x) = f(x, y0) é a curva intersecção da superfície que é o gráfico de
z = f ( x, y)
com o plano y = y0 = constante.
Consideremos os pontos P0 = (x0,y0) e P = (x0 + ∆x,y0) sobre a curva ϕ(x). A reta s
que passa por P0 e P, é uma reta secante à curva ϕ(x) e ao gráfico de f ( x, y).
O coeficiente angular
x x x
da reta s é dado por ms
x
=
ϕ( 0 + ∆ ) −ϕ(
0)
=
∆
f x x y f x y
( 0 + ∆ , 0) − ( 0, 0)
.
∆x
Se o ponto P desliza sobre ϕ(x) até coincidir com o ponto P0, P → P0, a reta secante,
s, passa a ser uma reta t, tangente à curva ϕ(x) e ao gráfico de f ( x, y)
, no ponto T = (x0,y0,z0), com
z0 = f(x0,y0). Seu coeficiente angular é dado por
ϕ( x0 + ∆x)
−ϕ(
x0)
f ( x0 + ∆x,
y0) − f ( x0, y0)
mt
= lim = lim = ϕ‘(x0) = fx(x0,y0)
∆x→
0 ∆x
∆x→
0 ∆x
Isso significa que a derivada parcial de f ( x, y),
em relação a x, no ponto P0 é igual
ao coeficiente angular da reta tangente à curva ϕ(x) e ao gráfico de z = f ( x, y)
, no ponto
T = (x0, y0, z0).
A reta t, tangente, pertence ao plano y = y0 = constante que é paralelo ao plano coordenado
x0z. Logo, o ângulo α que t forma com a reta y = y0 = constante, no plano x0y é o mesmo
ângulo que t forma com o eixo 0x. Portanto:
f ( P0)
fx ( x0, y0)
=
x
∂
= tg α = coeficiente angular da reta tangente ao gráfico de
∂
z = f ( x, y)
, no ponto T = (x0,y0,z0) e, paralela ao plano x0z.
Analogamente,
(b) Em relação a y:
A função ψ (y) = f(x0, y) é a curva intersecção da superfície que é o gráfico de
z = f ( x, y)
com o plano x = x0 = constante.
Consideremos os pontos P0 = (x0,y0) e P = (x0,y0 + ∆y) sobre a curva ψ(y). A reta s
que passa por P0 e P, é uma reta secante à curva ψ(y) e ao gráfico de f ( x, y).
O coeficiente angular
y y x
da reta s é dado por ms
y
=
ψ( 0 + ∆ ) −ψ(
0)
=
∆
f x y y f x y
( , 0 + ∆ ) − ( 0, 0)
.
∆y
Se o ponto P desliza sobre ψ(y) até coincidir com o ponto P0, P → P0, a reta secante,
s, passa a ser uma reta t, tangente à curva ψ(y) e ao gráfico de f ( x, y)
, no ponto T = (x0,y0,z0), com
z0 = f(x0,y0). Seu coeficiente angular é dado por
ψ( y0 + ∆y)
−ψ(
y0)
f ( x0, y0 + ∆y)
− f ( x0, y0)
mt
= lim = lim = ψ‘(y0) = fy(x0,y0)
∆y→
0 ∆y
∆y→
0 ∆y
Isso significa que a derivada parcial de f ( x, y),
em relação a y, no ponto P0 é igual
ao coeficiente angular da reta tangente à curva ψ(y) e ao gráfico de z =f( x, y)
, no ponto
T = (x0,y0,z0).

A reta t, tangente, pertence ao plano x = x0 = constante que é paralelo ao plano coordenado
y0z. Logo, o ângulo β que t forma com a reta x = x0 = constante, no plano x0y é o mesmo
ângulo que t forma com o eixo 0y. Portanto:
f ( P0)
fy ( x0, y0)
=
y
∂
= tg β = coeficiente angular da reta tangente ao gráfico de
∂
z = f ( x, y)
, no ponto T = (x0,y0,z0) e, paralela ao plano y0z
.
Exemplo:
Calcular o coeficiente angular da reta tangente ao gráfico de z = 7 − x 2 − y 2 + 2x + 2y,
(a) no ponto (2,3,4) e paralela ao plano x0z, isto é, na direção do eixo 0x;
(b) no ponto (2,3,4) e paralela ao plano y0z, isto é, na direção do eixo 0y;
(c) no ponto (1,1,9) e na direção do eixo 0x;
(d) no ponto (1,1,9) e na direção do eixo 0y.
Sol.:
As derivadas parciais de z = f ( x, y)
são:
fx(x,y) = −2x + 2 e fy(x,y) = −2y + 2
(a) A reta tangente em (2,3,4) e paralela ao plano x0z é uma reta que pertence ao plano y = 3
e tem como coeficiente angular fx(2,3) = − 4 + 2 = −2;
(b) A reta tangente em (2,3,4) e paralela ao plano y0z é uma reta que pertence ao plano x = 2
e tem como coeficiente angular fy(2,3) = − 6 + 2 = −4;
(c) A reta tangente em (1,1,9) e na direção do eixo 0x, é uma reta que pertence ao plano
y = 1 e tem como coeficiente angular fx(1,1) = − 2 + 2 = 0;
(a) A reta tangente em (1,1,9) e na direção do eixo 0y, é uma reta que pertence ao plano
x = 1 e tem como coeficiente angular fy(1,1) = − 2 + 2 = 0.
EQUAÇÕES DAS RETAS TANGENTES
(a) A equação da reta t1, tangente ao gráfico de z = f ( x, y)
, no ponto T = (x0,y0,z0) e paralela
ao plano x0z, é dada por:
⎧ x−x z−z ⎧x=
x
⎪ 0 0
0 + λ
=
⎪
Na forma simétrica ⎨ 1 f x ( x0, y0)
ou, na forma paramétrica ⎨y=
y0
.
⎩⎪ y = y
⎪
0
⎩ z= z + λf
( x , y )
0 x 0 0
(b) A equação da reta t2, tangente ao gráfico de z = f ( x, y)
, no ponto T = (x0,y0,z0) e paralela
ao plano y0z, é dada por:
⎧ y−y z−z ⎧ x = x
0 0
0
⎪ =
⎪
Na forma simétrica ⎨ 1 f y ( x0, y0)
ou, na forma paramétrica ⎨y
= y0+
λ .
⎩⎪ x = x
⎪
0
⎩ z = z0 + λ f y ( x0, y0)
Exemplo:
Determine as equações das retas tangentes ao gráfico de z = 7 − x 2 − y 2 + 2x + 2y,
(a) no ponto (2,3,4);
(b) no ponto (1,1,9).
Sol.:
Considerando os resultados do exemplo anterior, isto é, fx(2,3) = −2; fy(2,3) = −4;
fx(1,1) = 0 = fy(1,1), temos que:

⎧x
= 2 + λ
⎧ x = 2
⎪
⎪
(a) Paralela ao plano x0z é ⎨y
= 3 e, paralela ao plano y0z é ⎨y
= 3+
λ
⎪
⎩z
= 4−2λ ⎪
⎩ z = 4−4λ ⎧ x = 1+
λ
⎧ x = 1
⎪
⎪
(b) Paralela ao plano x0z é ⎨y
= 1 e, paralela ao plano y0z é ⎨y
=1+ λ
⎪
⎩ z = 9
⎪
⎩ z = 9
PLANO TANGENTE − RETA NORMAL
As retas tangentes t1 e t2, se interceptam no ponto T = (x0,y0,z0). Logo, determinam um plano
que passa por T e que contém as retas t1 e t2. Este plano é o plano tangente ao gráfico de
z = f ( x, y, z),
no ponto T. Sua equação geral é dada por
z - z0 = fx(x0,y0)(x− x0) + fy(x0,y0)(y− y0)
r r r
cujo vetor normal é n = v1× v2,
em que r v1 é o vetor diretor de t1 e, r v 2 é o vetor diretor de t2. Isto é,
r r r
i j k
r r r
r r r
n = v1× v2
= 1 0 fx( P0)
= −f x( P0) i − f y(
P0
) j+ k ou,
0 1 f ( P )
r r r r
n = fx( P0) i + f y(
P0
) j−k. y
0
Obs.: Para P = (x0 + ∆x, y0 +∆y) pertencente a uma vizinhança de P0, o valor de z = f ( x, y)
, isto é,
o valor de f(P) = f(x0 + ∆x, y0 +∆y) pode ser calculado, aproximadamente, sobre o plano tangente.
Ou seja, vale que z = f(x0 + ∆x, y0 +∆y) ≅ zplano.
A reta normal ao gráfico de z = f ( x, y)
no ponto T = (x0,y0,z0), tem como vetor diretor o
vetor r ⎧ x = x0 −λfx(
x0, y0)
⎪
n. Logo, suas equações paramétricas são ⎨y
= y0 −λf
y ( x0, y0)
e, as equações simétricas são
⎪
⎩z
= z0+
λ
⎧ x−x0 y−y0 ⎨
=
= z−z0. ⎩−
f x( x0, y0)
− f y(
x0, y0)
Exemplo:
Determine a equação do plano tangente e da reta normal ao gráfico da função z = 7 − x 2 − y 2
+ 2x + 2y nos pontos:
(a) (2,3,4) (b) (1,1,9)
Sol.:
(a) Considerando os resultados dos exemplos anteriores, isto é, que fx(2,3) = −2,
fy(2,3) = − 4 e que r v 1 = (1,0,−2) e r r r r
i j k
r r r
v 2 = (0,1,−4 ), temos que: n = v1 × v2
= 1 0 − 2 = 2
0 1 − 4
r i + 4 r j +
r
k é o vetor normal ao plano tangente. A equação do plano tangente é 2x + 4y + z + d = 0. Como o
ponto (2,3,4) pertence ao plano, 2.2 + 4.3 + 4 + d = 0, ou, d = −20. Logo, a equação do plano tangente
é 2x + 4y − z −20 = 0.
Se usarmos a equação envolvendo as derivadas parciais, temos que:
z − 4 = −2(x − 2) − 4(y − 3) ou que 2x + 4y + z −20 = 0.

⎧x
= 2+ 2λ
⎪
⎨ y = 3+ 4λ.
⎪
⎩ z = 4 + λ
A equação simétrica da reta normal é
⎧ x−2y−3 ⎨ = = z − 4 e, as paramétricas são
⎩ 2 4
(b) Considerando os resultados do exemplo anterior, isto é, fx(1,1) = fy(1,1) = 0, e que
r
v 1 = (1,0,0) e r r r r
i j k
r r r
v 2 = (0,1,0), temos que: n = v1× v2
= 1 0 0 = 0
0 1 0
r i + 0 r j − r k é o vetor normal ao
plano tangente. A equação do plano tangente é: − z + d = 0. Como o ponto (1,1,9) pertence ao plano
tangente, −9 + d = 0 ou que, d = 9. Logo, a equação do plano tangente é z −9 = 0 ou z = 9.
Se usarmos a equação envolvendo as derivadas parciais, temos que,
z − 9 = 0(x −1) + 0(y −1) ou que z − 9 = 0.
⎧ x = 0
⎪
As equações simétricas e paramétricas da reta normal são idênticas e valem ⎨ y = 0 .
⎪
⎩z
= 9 +λ
1.2) TAXA DE VARIAÇÃO
Vimos que não existe a derivada total de z = f ( x, y)
, no ponto P0 = (x0,y0) e, em
relação a x e a y, simultaneamente. Mas, podemos avaliar as variações de z em relação a x e, em
relação a y, em separado. Isto é:
(a) Em relação a x:
A taxa de variação média de z = f ( x, y)
entre os pontos P0 = (x0,y0) e
⎯→ ⎯
P = (x0 + ∆x,y0), isto é, na direção do vetor PP 0
∆z
=
∆x f ( P) − f ( P0)
=
∆x
ou, do eixo 0x, é dada por
f ( x0 + ∆x,
y0) − f ( x0, y0)
.
∆x
A taxa de variação instantânea ou apenas taxa de variação de z = f ( x, y)
, no ponto
P0 e na direção positiva do eixo 0x, é dada por
lim
f ( P) f ( P ) f ( x ∆x,
y ) f ( x , y )
z
lim f x ( x , y ) ( )
∆x
∆x
x P
− 0
0 + 0 − 0 0
= = 0 0 = 0
0
∂
∂
∆x→0∆x→ ou seja, a derivada parcial de z = f ( x, y),
em relação a x, no ponto P0 = (x0,y0), indica a variação
de z por unidade de variação de x, na direção positiva do eixo 0x, a partir de P0 = (x0,y0).
Analogamente:
(b) Em relação a y:
A taxa de variação média de z = f ( x, y)
entre os pontos P0 = (x0,y0) e
⎯→ ⎯
P = (x0,y0 +∆y), isto é, na direção do vetor PP 0
ou, do eixo 0y, é dada por
∆z
f ( P) − f ( P0)
f ( x0, y0+ ∆y)
− f ( x0, y0)
= =
.
∆y∆y ∆y
A taxa de variação instantânea ou apenas taxa de variação de z = f x y
( , ) , no ponto
P0 e na direção positiva do eixo 0y, é dada por

f ( P) f ( P)
f ( x , y ∆y)
f ( x , y )
z
lim lim fy( x , y ) ( )
∆y ∆y
∆y
∆y
y P
− 0
0 0+ − 0 0
= = 0 0 = 0
→0→0 ∂
∂
ou seja, a derivada parcial de z = f ( x, y),
em relação a y, no ponto P0 = (x0,y0), indica a variação
de z por unidade de variação de y, na direção positiva do eixo 0y, a partir de P0 = (x0,y0).
Exemplo:
1) A temperatura do ponto (x,y) de uma placa metálica plana é dada por
2 2
T(x,y) = 40 − 43−2x −4y
(T em 0 C, x e y em cm)
(a) Determine a temperatura no ponto (3,2) e a equação da isoterma que passa por este ponto;
(b) Qual é a taxa de variação da temperatura em relação a x e a y?
(c) Qual é a temperatura aproximada dos pontos (4,2); (3,3); (2,2) e (3,1)?
Sol.:
2 2
(a) T(3,2) = 40 − 43−2( 3) −4(
2)
= 40 −3 = 37 0 C
A isoterma que passa pelo ponto (3,2) é a equação de todos os pontos que tem temperatura
37 0 C, isto é, a curva de nível T(x,y) = 37 . Substituindo e desenvolvendo obtemos:
2 2
40 − 43−2x −4y
= 37 ou (3) 2 = 43 − 2x 2 − 4y 2 ou 2x 2 + 4y 2 = 34.
(b) (i) Em relação a x:
∂T
∂x
= Tx(x,y)
− 4x
= −
2 2
2 43−2x −4y
=
2x
e, no ponto (3,2),
2 2
43−2x −4y
∂T(,)
32
= Tx (,) 32 =
∂x
2(3) 6
=
9 3 = 2 0 C/cm. (Temperatura aumenta de 2 0 C por cm)
(ii) Em relação a y:
∂T
− 8y
= Ty( x, y)
= −
∂y
2 2
2 43−2x −4y
=
4y
e, no ponto (3,2),
2 2
43−2x −4y
∂T(,)
32
42 ( )
= Ty (,) 32 = =
∂y
9
8
3 ≅ 2,66 0 C/cm. (Temperatura aumenta de 2,66 0 C por cm)
(c) Os valores aproximados das temperaturas são:
T(4,2) ≅ 37 0 C + 2 0 C.1cm = 37 0 C + 2 0 C = 39 0 C
T(3,3) ≅ 37 0 C + 2,66 0 C.1cm = 37 0 C + 2,66 0 C = 39,66 0 C
T(2,2) ≅ 37 0 C + 2 0 C.(−1)cm = 37 0 C − 2 0 C = 37 0 C
T(3,1) ≅ 37 0 C + 2 0 C.(−1)cm = 37 0 C − 2,66 0 C = 36,34 0 C.
2) DA FUNÇÃO w = f(x,y,z)
Vimos que esta função não tem representação geométrica (gráfico). Logo, só podemos
interpretar suas derivadas parciais através da taxa de variação. Isto é:
(a) Em relação a x:
A taxa de variação média da função w = f ( x, y, z)
entre os pontos P0 = (x0,y0,z0) e
P =(x0 + ∆x,y0,z0) é dada por ∆w
f ( x0 + ∆x,
y0, z0) − f ( x0, y0, z0)
=
. Logo, a taxa de variação
∆x
∆x
instantânea ou apenas taxa de variação de w = f ( x, y, z),
a partir de P0 e na direção de P0 a P, isto
é, na direção positiva do eixo 0x, é dada por

f ( x0 + ∆x,
y0, z0) − f ( x0, y0, z0)
lim = f x ( x0, y0, z0)
∆x→
0
∆x
que indica o quanto varia w por unidade de variação de x, a partir de P0, na direção positiva do eixo
0x.
(b) Analogamente, a derivada parcial de w = f ( x, y, z)
no ponto P0 e em relação a y, indica
a taxa de variação de w por unidade de variação de y, a partir de P0, na direção positiva do eixo 0y
e,
(c) A derivada parcial de w = f ( x, y, z),
no ponto P0 e em relação a z, indica a taxa de variação
de w em relação a variação de z, a partir do ponto P0 e, na direção positiva do eixo 0z.
GENERALIZAÇÃO
Para w = f(x1,x2, . . ., xn), interpretamos cada derivada parcial como sendo a taxa de variação
de w por unidade de variação da respectiva variável xi, i = 1,2, ..., n, a partir do ponto P0 e na
direção positiva do eixo xi.
Exemplo:
1) O volume de um tronco de cone reto, com altura h, raio da base (maior) R e raio menor r,
é dado pela função V(h,r,R) = π 2 2
hr ( + rR+ R ) (V em unidades de volume e h,r,R em unidades
3
lineares)
Em um determinado instante temos um tronco de cone de dimensões h = 10 cm, r = 2 cm e
R = 5 cm.
(a) Qual é o volume tronco do cone?
(b) Se variarmos só a altura, qual é a variação do volume?
(c) Se variarmos só o raio menor, qual é a variação do volume?
(d) Qual é a variação do volume em relação ao raio da base?
Sol.:
π
(a) O volume do tronco do cone é V = 10( 4 10 25) = 130π
3 + + cm3 .
(b) ∂V
π 2 2
= Vh( h, r, R) = ( r + rR+ R ) e Vh(10,2,5) = 13π cm
∂h
3
3 /cm.
(c) ∂V
π
= Vr( h, r, R) = h( 2 r+ R)
e Vr(10,2,5) = 30π cm
∂r
3
3 /cm.
(d) ∂V
π
= VR( h, r, R) = h( r+ 2R)
e VR(10,2,5) = 40π cm
∂R
3
3 /cm.
2) O potencial elétrico dos pontos (x,y,z) de uma região do espaço é dado por
2 2 2
V( x, y, z) = ln x + y + z
(V em volts; x,y e z em cm)
(a) Determine o potencial elétrico do ponto (1,2,2);
(b) Qual é a superfície equipotencial que passa pelo ponto (1,2,2)?
(c) Quais são as taxas de variação do potencial V, no ponto (1,2,2), em relação as variações
de x, y e z?
Sol.:
2 2 2
(a) V (,,) 122 = ln1
+ 2 + 2 = ln3 = 1,0986 volts.
(b) A equação da superfície equipotencial é dada por V(x,y,z) = ln3 (é uma superfície de nível)

2 2 2
Substituindo e desenvolvendo, ln x + y + z = ln3 ou x 2 + y 2 + z 2 = 3 2 , isto é, todos
os pontos que pertencem à esfera de centro na origem e raio 3 têm o mesmo potencial elétrico e
ln3 volts.
(c) As taxas de variação são dadas pelas derivadas parciais no ponto (1,2,2), isto ë:
(i) Em relação a x:
2x
∂V
2
= Vx( x, y, z)
=
∂x
volts/cm.
2 2 2
x + y + z
x + y + z
=
x
x
+ y + z
(ii) Em relação a y:
2 2 2 2 2 2
2y
∂
2 2 2
V
2 x + y + z y
= Vy( x, y, z)
= =
∂y
x + y + z x + y + z
(iii) Em relação a z:
2 2 2 2 2 2
2z
∂
2 2 2
V
2 x + y + z z
= Vz( x, y, z)
= =
∂z
x + y + z x + y + z
EXERCÍCIOS PROPOSTOS
2 2 2 2 2 2
e Vx(1,2,2) =
2
e Vy(1,2,2) =
1 + 2 + 2
2 2 2
2
e Vz(1,2,2) =
1 + 2 + 2
2 2 2
1) Calcular as derivadas parciais de terceira ordem das seguintes funções:
a) f ( x, y)
= x 4 + 5y 3 + 3x 2 y + 8xy b) f ( x, y)
= x 3 cosy + 4y 2 senx
c) f ( x, y)
= ln(x + y) d) z = x 3 e 5y
e) z = cos(3x + 5y) f) z = ln(x 2 + y)
g) z = e x cosy h) z = e x seny
2 2 y
i) z = ( x + y ) arctg
x
x− j) z = ln
x+ 2 2
x − y
2 2
x − y
2) Calcular as derivadas parciais de segunda ordem das seguintes funções:
a) z = arcsen y
2
x
b) w = xy + yz + zx
c) z = x a y b z c d) w =
2 2 2
x + y + z
3) Verifique se ∂
2 2
z ∂ z
= para:
∂∂ xy ∂∂ yx
a) z = arcsen
x− y
x
b) z = 2xy
+ y
x+ y
c) z = arctg
1−
xy
d) z = x y
2
1
1
+ 2 + 2
2 2 2
=
1
9
2
= volts/cm.
9
2
= volts/cm.
9

⎧ 2 2
⎪
x − y
xy , ( xy , ) ≠ ( , )
4) a) Mostre que para a função f ( x, y)
= ⎨ 2 2 se 00
x + y
, temos fxy(0,0) = −1 e
⎩⎪ 0 se ( xy , ) = ( 00 , )
fyx(0,0) = 1;
b) Dada a função z = ye x2
, calcular ∂
4
z
2 2
∂x ∂y
;
c) Mostre que a função z = x 3 − 2xy 2 2
2
∂ z ∂ z ∂z
verifica a equação x 2 + y = 2 ;
∂x
∂∂ yx ∂x
2
2
2
y y
2 ∂ z ∂ z 2 ∂ z
d) Mostre que a função z = x + verifica a equação x 2 + 2xy + y 2 = 0;
x x
∂x
∂∂ xy ∂y
e) Mostre que a função z = tg(y + kx) + (y − kx) 3/2 verifica a equação da corda vibrante,
2
2
∂ z 2 ∂ z
2 = k 2 ;
∂x
∂y
f) Quando dois resistores de resistências R1 ohms e R2 ohms são conectados em paralelo, sua re-
RR 1 2
= . Mostre que
R1 + R2
∂
2 2
2
R ∂ R 4R
2 2 = 4
∂R1
∂R2
( R1 + R2)
sistência combinada R em ohms é R
5) Se f ( x, y)
admite derivadas parciais de segunda ordem, chama-se Laplaciano de f à função:
r
2
2
2 ∂ f ∂ f
∇ f ( x, y)
= 2 ( xy , ) + 2 ( xy , )
∂x
∂y
Calcule r ∇ 2 f ( x, y)
para as seguintes funções:
a) f ( x, y)
= x 4 − y 4 b) f ( x, y)
= sen(x 2 − y 2 ) c) f ( x, y)
=
1
2 2
x + y
d) f ( x, y)
=
2x
x + y
2 2
e) f ( x, y)
= arctg y
x
f) f x y ( , ) = excosy 6) Encontre o coeficiente angular da reta tangente à curva intersecção do gráfico de z
2 2
= 10 − x −2y
com o plano y = 1 no ponto em que x = 2.
7) Dada a função f ( x, y) = y
x y
2
a) O domínio de f;
+
1
2 2
+
, pede-se determinar:
b) As derivadas parciais fx(3,4) e fy(3,4);
c) O coeficiente angular da reta tangente à curva que é a intersecção do gráfico de f com o
plano x = 3 no ponto em que y = 4.
8) Determine a equação do plano tangente e da reta normal às seguintes superfícies:
a) z = x 2 − 4y 2 , no ponto P0 = (5,−2) b) z = x 2 + y 2 , no ponto P0 = (3,4)
c) z = x 2 + y 2 − 4x − 6y + 9, no ponto em que o plano tangente é paralelo ao plano x0y.
9) Através da equação do plano tangente, encontre um valor aproximado para:
a) (1,02) 3 (0,97) 2 b) (0,998) 3 1,003 c) ( 405 , ) + ( 293 , )
3 2 3
d) 8, 002 3, 96 e)
24, 936
81, 082
2 2
f) 36, 24 tg44 0 40’
10) Um ponto move-se ao longo da intersecção do parabolóide elíptico z = x 2 + 3y 2 e o plano x = 2.
A que taxa está z variando em relação a x quando o ponto está em (2,1,7)?

11) Um ponto move-se ao longo da intersecção do plano y = 3 e superfície z =
2 2
29−
x − y . Qual
é a taxa de variação de z em relação a x e em relação a y quando o ponto está em (4,3,3)?
12) A temperatura do ponto (x,y) de uma chapa metálica plano é dada por
2 2
T( x, y) = 30 + 50 − x − y . (T em 0 C, x e y em cm)
a) Determine o domínio de T(x,y) e a temperatura no ponto (3,4);
b) Determine a equação da isoterma que passa pelo ponto (3,4) e a represente no plano x0y;
c) Se a partir do ponto (3,4) um formiga caminhar na direção do eixo 0x, sentido positivo, a
temperatura aumentará ou diminuirá? De quantos graus por centímetro aproximadamente?
13) Em uma livraria, o lucro mensal L é uma função do número de vendedores, x, e do capital investido
em livros, y, (y em milhares de reais). Em uma certa época tem-se: L(x,y) = 400 − (12 − x) 2 −
(40 − y) 2 .
a) Calcule o lucro diário se a empresa tem 7 vendedores e 30 mil reais investidos;
b) Calcule ∂L
∂L
( 730 , ) e ( 730 , ) ;
∂x
∂y
c) O que é mais lucrativo, a partir da situação do item (a):
− aumentar de uma unidade o número de vendedores, mantendo o capital investido;
− ou investir mais 1 mil reais, mantendo o número de vendedores?
14) A temperatura do ponto (x,y) de uma chapa é dada por T(x,y) = 2x 2 + 3y 2 + 15, (T em 0 C, x e y
em cm).
a) Determine a equação da isoterma que passa por (1,2);
b) Se a partir do ponto (1,2) nos movermos no sentido positivo do eixo 0x, a temperatura
aumenta ou diminui? De quantos 0 C por cm, aproximadamente?
c) Em que ponto (a,b) a temperatura vale 45 0 C, sendo a taxa de variação da temperatura em
relação à distância percorrida na direção do eixo 0y, sentido positivo, igual a 12 0 C/cm? (considere a
e b positivos).
15) Uma fábrica produz mensalmente x unidades de um produto A e y unidades de um produto B,
2 2
sendo o custo mensal da produção conjunta dado por C( xy , ) = 20. 000 + x + y (C em reais).
Em um certo mês, foram produzidas 3.000 unidades de A e 2.000 unidades de B.
a) Calcule o custo da produção neste mês;
b) Calcule ∂C
∂C
e ;
∂x
∂y
c) O que é mais conveniente, a partir desta situação: aumentar a produção de A mantendo
constante a de B, ou aumentar a de B mantendo constante a de A? Justifique com base nos resultados
de (b).
16) A superfície de um lago é representada por uma região D no plano x0y, de modo que a profundidade
sob o ponto (x,y) é dada por f ( x, y)
= 300 − 2x 2 − 3y 2 , (unidades em metros). Se um esquiador
aquático está na água no ponto (4,9), ache a taxa de variação da profundidade na direção leste e na
direção norte.
100
17) O potencial elétrico V no ponto (x,y,z) é dado por V( x, y, z)
= 2 2 2
x + y + z
em cm).
Ache a taxa de variação de V, no ponto (2,−1,1) na direção:
a) do eixo 0x b) do eixo 0y c) do eixo 0z
(V em volts, x, y e z

V
18) A análise de certos circuitos elétricos envolve a fórmula I =
, em que I é a corrente,
2 2 2
R + L ω
V a voltagem, R a resistência, L a indutância e ω uma constante positiva. Ache e interprete ∂I
∂R
e
∂I
∂L
.
E
19) A resistência R ohms de um circuito elétrico é dada pela fórmula R = , em que I é a corrente
I
em ampères e E é a força eletromotriz em volts. Calcule e interprete o significado de ∂R
∂R
e
∂I
∂E
quando I = 15 ampères e E = 110 volts.
20) A maioria dos computadores tem apenas um processador que pode ser utilizado para cálculos.
Os supercomputadores modernos, entretanto, têm entre dois e vários milhares de processadores. Um
supercomputador multiprocessador é comparado a um computador uniprocessador em termos de
speedup. A speedup S é o número de vezes mais rápido que um cálculo pode ser feito com um multiprocessador,
do que com um uniprocessador. A lei de Amdahl é uma fórmula usada para determinar
S
p
S( p, q)
=
q+ p( 1−q)
em que p é o número de processadores e q é a fração do cálculo que pode ser realizada utilizando
todos os processadores disponíveis em paralelo − isto é, usando-os de maneira que os dados sejam
processados concomitantemente por unidades separadas. A situação ideal, paralelismo completo,
ocorre quando q = 1.
a) Se q = 0,8, ache a speedup quando p = 10; 100 e 1.000. Mostre que a speedup S não pode
exceder a 5, independente do número de processadores disponíveis.
b) Ache a taxa instantânea de variação de S em relação a q.
c) Qual a taxa de variação em (b) se há paralelismo completo, e como o número de processadores
afeta esta taxa de variação?
d) A eficiência E de um cálculo por multiprocessador pode ser calculada pela equação:
S( p, q)
E( p, q)
=
p
Mostre que, se 0 ≤ q < 1, E(p,q) é uma função decrescente de p e, portanto, sem paralelismo completo,
o aumento de número de processadores não aumenta a eficiência do cálculo.
21) No estudo da penetração da geada em uma rodovia, a temperatura T no instante t horas e à profundidade
x pode ser dada, aproximadamente, por
−λx
T( x, t) = T0e sen( ωt −λ
x)
em que T0, ω e λ são constantes. O período de sen(ωt − λx) é 24 horas.
a) Calcule e interprete ∂T
∂T
e .
∂x
∂t
b) Mostre que T verifica a equação unidimensional do calor ∂
2
T ∂ T
= k 2 em que k é uma
∂t
∂x
constante.
22) A capacidade vital V dos pulmões é o maior volume de ar que pode ser exalado após uma inalação
de ar. Para um indivíduo do sexo masculino com x anos de idade e y centímetros de altura, V
pode ser aproximada pela fórmula V(x,y) = 27,63y − 0,112xy.
Calcule e interprete o significado de ∂V
∂V
e .
∂x
∂y

23) Em um dia claro, a intensidade de luz solar (em velas-pé) às t horas após o nascente e à profun-
−kx
3 t
didade oceânica de x metros, pode ser aproximada por: I( x, t) = I0e sen ( )
D
π em que I0 é a
intensidade de luz ao meio-dia, D é a extensão do dia (em horas) e k é uma constante positiva. Se
I0 = 1.000, D = 12 e k = 0,1, calcule e interprete ∂I
∂I
e quando t = 6 e x = 5.
∂t
∂x
24) O volume V de um cone circular reto é dado por V = x y x
π 2 2 2
4 − em que y é o compri-
24
mento da geratriz e x é o diâmetro da base. Encontre a taxa de variação do volume em relação à geratriz
e do volume em relação ao diâmetro quando x = 16 cm e y = 10 cm.