10 v v v v   arccos cos OAAOv      v  vvv v  180 ...

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
10
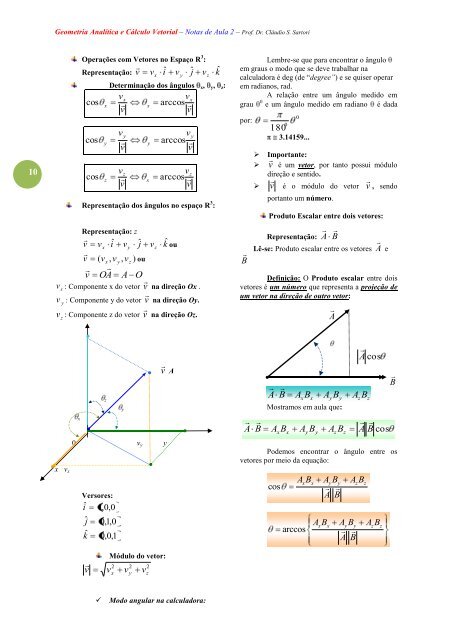
Operações com Vetores no Espaço R 3 :
Representação: v v iˆ
v ˆj
v
cos
cos
cos
x
y
z
x
y
z
kˆ
Determinação dos ângulos x, y, z:
vx
v
vy
v
vz
v
x
y
x
vx
arccos
v
vy
arccos
v
vz
arccos
v
Representação dos ângulos no espaço R 3 :
Representação: z
v v iˆ
v ˆ
x y
j vz
kˆ
ou
v ( vx
, v
y
, vz
) ou
v OA A O
v : Componente x do vetor v na direção Ox .
x
v : Componente y do vetor v na direção Oy.
y
v
z
: Componente z do vetor v na direção Oz.
Lembre-se que para encontrar o ângulo
em graus o modo que se deve trabalhar na
calculadora é deg (de “degree”) e se quiser operar
em radianos, rad.
A relação entre um ângulo medido em
grau
0 e um ângulo medido em radiano é dada
por:
B
0
0
180
3.14159...
‣ Importante:
‣ v é um vetor, por tanto possui módulo
direção e sentido.
‣ v é o módulo do vetor v , sendo
portanto um número.
Produto Escalar entre dois vetores:
Representação:
A
B
Lê-se: Produto escalar entre os vetores A e
Definição: O Produto escalar entre dois
vetores é um número que representa a projeção de
um vetor na direção de outro vetor:
A
x v x
x
z
0 v y y
Versores:
î 1,0,0
ĵ
ˆk
0,1,0
0,0,1
v
y
Módulo do vetor:
2
x
v
2
y
v
2
z
v A
A B
Ax
Bx
Ay
By
Mostramos em aula que:
A B
A B
x
x
A B
y
y
A B
z
z
A
cos
A B
z
z
A B cos
Podemos encontrar o ângulo entre os
vetores por meio da equação:
cos
arccos
A B A B A B
AB
x x y y z z
A B A B A B
AB
x x y y z z
B
v Modo angular na calculadora:

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
11
Aplicações:
Trabalho de uma força:
O trabalho de uma força, ao deslocar um corpo
de uma posição r 1
a outra r 2
no espaço ao longo de
uma trajetória C é dado por:
C
F
dr
Quando a força é constante ao longo dessa
trajetória, sendo d o deslocamento sofrido pelo corpo:
B .
Propriedades:
F
d
Potência de uma força:
P
F
v
i ˆ iˆ
1 i ˆ ˆj
ˆj
iˆ
0
ˆj ˆj
1 i ˆ kˆ
kˆ
iˆ
0
k ˆ k ˆ 1 ˆj
kˆ
kˆ
ˆj
0
A B C A B A C
v
nˆ ; onde v AB B A
AB v v
nˆ
AB
(Normalização de um vetor).
cos
Mostre que:
x
iˆ
cos
y
ˆj
cos
z
kˆ
Produto Vetorial entre dois vetores:
‣ Representação:
A
B
Lê-se: Produto vetorial entre os vetores A e
Definição: O Produto vetorial entre dois
vetores é um vetor que possui direção perpendicular ao
plano formado pelos vetores A e B , cujo ângulo vale
e cujo módulo é igual a área formada pelo
paralelogramo de lados A e B :
A
A
θ
B
h
A sen
B
A
B
A
B
iˆ
A
B
x
x
ˆj
A
B
Mostramos em aula que:
A B
y
z
A B iˆ
z
y
A B
z
x
y
y
A B
x
kˆ
A
B
z
z
z
ˆj
A B
Podemos encontrar o módulo do vetor que
é originado pelo produto vetorial dos vetores
vetores A e B :
A
B
‣ Aplicações:
A B sen
Torque ou Momento de uma força
aplicada num ponto A em relação a um ponto
O:
M
OA
y
OA
F
x
A
y
A B kˆ
y
F A
A
z O x
11. Força magnética sobre uma
partícula de carga q que penetra numa região
de Campo Magnético Uniforme.
Força de Lorentz:
F qE qv B
q E v B
Propriedades:
0 iˆ
ˆj
ˆj
iˆ
ˆ
ˆj ˆj
0 kˆ
iˆ
iˆ
kˆ
ˆj
ˆ ˆ ˆ j kˆ
kˆ
ˆj
ˆ
i ˆ iˆ
k
k k 0
i
A B C A
A
B B A
mA B m A
A B C A
A B C A
A
A
0
B
A
B
B C
C B
C
A
B C
x

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
Produto misto de três vetores:
O Produto misto entre os vetores A , B e C
é um número cujo valor é o volume do paralelepípedo
formado pelo comprimento dos respectivos vetores .
‣ Interpretação Geométrica:
‣ Notação: A B C
Funções com valores Vetoriais:
Se D é um conjunto de números reais,
então, r x(
t)ˆ
i y(
t)
ˆj
z(
t)
kˆ
é uma função
com valores vetoriais para um dado t real.
Se t é o tempo, denominamos o vetor
deslocamento:
r x(
t)ˆ
i y(
t)
ˆj
z(
t)
kˆ
A trajetória de uma partícula para esse
vetor deslocamento é a união de todos os extremos
desses vetores para todo instante de tempo t.
12
A
B
C
A
B C sen
cos
A
B
C
A
B
C
x
x
x
A
B
C
y
y
y
A
B
C
z
z
z
O vetor velocidade instantânea é um vetor
tangente à trajetória e é dado por:
v(
t)
dr
dt
v
( t)
dx
iˆ
dt
Observe que:
v iˆ
x
v
y
dy
ˆj
dt
ˆj
v kˆ
z
dz
kˆ
dt
v x
v y
dx
dt
dy
dt
v z
dz
dt
O vetor aceleração instantânea é dado
por:
2 2 2
2
d r d x d y d z
a ( t)
iˆ
ˆj
kˆ
2 2 2
dt dt dt dt
2
a
( t)
Observe que:
a iˆ
x
a
y
ˆj
a kˆ
z
a
a
a
x
y
z
dv
dt
dv
dt
x
y
dv
dt
z

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
Exercícios de Aplicação:
Desenvolvidos em aula
Em cada ilustração, encontre o que se pede:
1.
(d) AC AD 298.72
(e) Ângulo entre
(f) Ângulo entre
0
AC e AD :59.8 .
0
OA e OB : 90
(a) AD AB (b) AC
AD
2. O ponto A está a 20m do chão.
(c) AD AB
(d) AC AD
(e) Ângulo entre
AC e AD .
13
(f) Ângulo entre
OA eOB .
O
A(0, 20, 0);B(-4, 0, 5); C(12, 0, 3.6);D(-4, 0, -14.8)
AD D A 4,0, 14.8 0,20,0 4, 20, 14.8
AB B A 4,0,5 0,20,0 4, 20,5
AC C A 12,0,3.6 0,20,0 12, 20,3.6
(a)
iˆ
ˆj kˆ
AD AB 4 20 14.8
4 20 5
iˆ ˆj kˆ
iˆ ˆj
4 20 14.8 4 20
4 20 5 4 20
(a) AC AB (b) AB AC
(c) AC AB
(e) Ângulo entre
(f) Ângulo entre
3.
(d) OC OD
AC e AB .
OA eOB .
AD AB 20 5 20 14.8 i ˆ ’
ˆ
14.8 4 5 4 j
ˆ
4 20 4 20 k
AD AB 396i ˆ 79.2 ˆj 0k
ˆ
(b)
AC AD 368i ˆ 163.2 ˆj 320k
ˆ
(c) AD AB 342
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OD

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
(e) Ângulo entre
(f) Ângulo entre
AC e AB .
OA eOB .
4.
14
(a) AC AB (b) AB AC
(c) AC AB
(e) Ângulo entre
(f) Ângulo entre
(g) AE
AC
(d) OC OD
AC e AB .
OA eOE .
(a) AC AB (b) AB AC
(c) AC AB
(e) Ângulo entre
(f) Ângulo entre
(g) AB
7.
AC
(d) OC OD
AC e AB .
OA eOD .
5.
(a) AC AB (b) AB AC
(c) AC AB
(e) Ângulo entre
(f) Ângulo entre
(g) AD
6.
AC
(d) OC OD
AC e AB .
OA eOB .
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OD

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
(e) Ângulo entre
(f) Ângulo entre
(g) AD AE
AC e AB .
OE eOF .
10.
8.
15
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OD
11.
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OD
9. O raio do disco é 5cm.
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OD
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OD

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
12.
14.
16
(a) OA OB (b) OA OA
(a) AC AB (b) AB AC
(c)OA OB
(d) OA OA
(c) AC AB
13.
(d) OC OA
15.
(a) AC AB (b) AB AC
(a) AC
AB (b) AB AD
(c) AC AB (d) OC OA
(c) AC AB
(e) Ângulo entre
(f) Ângulo entre
(g) AD AE
(d) OC OD
AC e AB .
OE eOF .

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
16.
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OD
18.
17
(a) AC AB (b) AB AC
(c) AC AB
(e) Ângulo entre
(f) Ângulo entre
(g) AD AE
(d) OC OD
AC e AB .
OE eOB .
(a) AC AB (b) AB AC
(c) AC AB (d) OC OD
19.
17.
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OB
20.

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
PROBLEMAS
‣ Parte A – Exercícios de treinamento
18
Problema 1 – São dados os vetores:
u 3ˆ i ˆj
v 2ˆ i 5 ˆj
r 2ˆ i 3ˆj
kˆ
s 4ˆ i 2 ˆj
8kˆ
Determine:
(a) u
3 v
(b) u
v
(c) u ( u 2v)
(d)
(e)
(f)
(g)
(h)
u 2 v 3r
u
r v
v s v r u
v s v r u
v s v r u iˆ
(a) AC AB (b) AB AC
(c) AC AB (d) OC OB
21.
Problema 2 – São dados os vetores:
A
B
e C
iˆ
4 ˆj
3k
2ˆ i 3 ˆj
kˆ
5ˆ i 2 ˆj
3kˆ
Verifique as propriedades:
i. A B C A B A C
ii. A B B A
iii. mA B m A B
iv. A B C A B C
v. A B C A C B A B C
vi.
A
A
0
Problema 3 – Encontre os ângulos entre
os vetores:
(a) A e B .
(b) A e C .
(c) B e C .
r
( t)
Problema 4 – Seja:
(9 4t)ˆ
i ( 4 6t) ˆj
(3
3t)
kˆ
:
(a) AC AB (b) AB AC
(c) AC AB
(d) OC OB
(a) Encontre os vetores:
r (0) ; r (1)
e r (2)
.
(b) Esboce os vetores: r (0)
; r (1)
e r (2)
.
(c) Encontre os vetores

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
19
v (0) ; v (1)
e v (2)
.
Problema 5 – Seja:
r
( t)
acostiˆ
asentj ˆ btkˆ
, com a e b
constantes.
(a) Faça o traçado de r (t)
completando a
tabela abaixo:
t r (t)
0
/4
/2
3 /4
5 /4
2
(b) Esquematizando a curva que representa a
trajetória, união de vários pontos extremos do vetor
r (t) , dada para a = 1 e b = 1/3, teremos:
t r (t)
-2
-1
0
1
2
3
4
Indique os vetores da tabela na figura que
representa a trajetória C.
v
( t)
c) Calcule o vetor velocidade instantânea
v iˆ
x
seus módulos.
instantânea
v
y
ˆj
para os instantes da tabela e
d) Determine o vetor aceleração
a
( t)
a iˆ
da tabela e seus módulos.
x
a
y
ˆj
para os instantes
-0.5
-1
0.5
0
-1 1 -0.5 0 0.5
1
6
4
2
0
0.5 1
-0.5 -1
0
-10
-5
0
-10
0
Indique os vetores da tabela na figura que
representa a trajetória C.
5
10
Problema 6 – Uma partícula de carga q
penetra numa região onde há um campo elétrico
N
E 3ˆ i 4ˆj
6kˆ
, e um campo magnético
C
B 0.2ˆ i 0.4 ˆj
T .
F
Encontre a relação se a velocidade desta
q
partícula é de v 12ˆ i 22 ˆj
.
m
s
Problema 7 – Seja r t tiˆ
2
( ) 2 (8 t ) ˆj
.
(a) Faça o traçado de r (t)
completando a
tabela a seguir:

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
‣ Parte B – Trabalho.
Problema 1 - Dados os vetores P = 3i - j + 2k,
Q = 4i + 5j - 3k e S = -2i + 3j - k, calcule os produtos
escalares P • Q, P • S e Q•S.
Problema 2 - Calcule o produto escalar
P 1 • P 2 e utilize o resultado obtido para provar
a identidade:
cos(
1 2)
cos
1
cos
2
sen
1
sen
2
(b) a projeção sobre AB da força aplicada
pelo cabo A
Problema 8 - Sabendo que a força de
tração no cabo AD é de 810 N, determine: (a)
o ângulo entre AD e o mastro AB e
(b) a projeção sobre AB da força exercida
pelo cabo AD no ponto A.
20
1
P 2
2
P 1
x
Problema 3 - Três cabos são utilizados para
sustentar um recipiente, como ilustrado. Determine o
ângulo formado pelos cabos AB e AD.
Problema 4 - Três cabos são utilizados para
sustentar um recipiente, como ilustrado. Determine o
ângulo formado pelos cabos AC e AD.
Problema 5 - O tubo AB pode deslizar ao
longo do eixo horizontal. Os extremos A e B do tubo
estão ligados ao ponto fixo C por meios de elásticos. Na
posição correspondente a x = 280 mm, determine o
ângulo formado pêlos dois elásticos
(a) usando o produto escalar entre vetores
apropriados.
(b) aplicando a lei dos co-senos ao triângulo
ABC.
Problema 9 - Dados os vetores P = 3i - j +
2k, Q = 4i + 5j - 3k e S = -2i + 3j - k, calcule:
(a) (Q x S)
(b) (P x Q) • S
(c) (S x Q) • P.
Problema 10 - Dados os vetores P = 4i - 2j
+ 3k, Q = 2i + 4j - 5k e S = si - j + 2k, determinar
o valor de s para o qual os três vetores são
coplanares.
Problema 11 - Sabendo que a força de
tração no cabo AB é de 570 N, determine o
momento, em relação a cada um dos eixos
coordenados, da força aplicada no ponto 6 da
placa.
Problema 12 - Sabendo que a força de
tração no cabo AC é de 1 065 N, determine o
momento da força aplicada no ponto C da placa,
em relação a cada eixo coordenado.
Problema 6 - Resolva o Problema 3.30
quando x = 100 mm.
Problema 7 - Sabendo que a força de tração
no cabo AC é de 1 260 N, determine:
(a) o ângulo entre o cabo AC e o mastro AB e

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
21
Problema 13 - Um pequeno barco pende de
dois suportes, um dos quais é mostrado na figura. Sabese
que o momento, em relação ao eixo z, da força
resultante R aplicada no ponto A do suporte não deve
exceder o valor de 217 N • m, em valor absoluto.
Determine o maior valor possível da força de tração no
cabo ABAD quando x = 1,46m.
t r (t)
0
/4
/2
3 /4
5 /4
2
(b) Esquematizando a curva que
representa a trajetória, união de vários pontos
extremos do vetor r (t)
, dada para a = 1 e b = 1/3,
teremos:
-0.5
-1
-1 -0.5 0 0.5 1
0.5
1
0
4
Problema 14 - Com referência ao Prob. 3.38,
determine o maior valor de x compatível com uma
força de tração de 214 N no cabo ABAD.
Problema 15 - Uma força única P atua no
ponto C em uma direção perpendicular ao cabo BC da
manivela da figura. Sabendo que M x = 20 N • m, M y =
8,75 N • m e M z =30 N • m, determine o módulo de P e
os valores de e .
Problema 16 - Uma única força P atua no
ponto C em uma direção perpendicular ao cabo BC da
manivela da figura. Determine o momento M de P em
relação ao eixo x, quando = 70 0 , sabendo que M y = -
20 N • m e M z = -37,5 N • m.
Problema 17 – Seja:
r
( t)
asentiˆ
acos
ˆj
btkˆ
, com a e b
constantes.
(a) Faça o traçado de r (t)
completando a tabela
abaixo:
2
0
Indique os vetores da tabela na figura.
Problema 18 – Determine a
velocidade vetorial v (t)
, se
r
( t)
asentiˆ
acos
ˆj
btkˆ
representa
vetor posição de uma partícula em movimento.
Problema 19 – Uma partícula de
carga q penetra numa região onde há um campo
N
elétrico E 3ˆ i 4ˆj
6kˆ
, e um campo
C
magnético B 0.01ˆ i 0.4 ˆj
T .
F
Encontre a relação se a
q
velocidade desta partícula é de
v 20ˆ i 10ˆj
5kˆ
.
m
s
Problema 20 – Seja o vetor posição de uma
partícula dado por:
r
( t)
costiˆ
sentj ˆ 1kˆ
A trajetória dessa partícula está indicada na
figura.
(a) Calcule o vetor velocidade instantânea
v
( t)
v iˆ
x
v
y
ˆj
e t 3 = 4 s, e também seus módulos.
para os instantes t 0 = 0s, t 1 = 2s
o

Geometria Analítica e Cálculo Vetorial – Notas de Aula 2 – Prof. Dr. Cláudio S. Sartori
a
( t)
módulos.
(b) Determine o vetor aceleração instantânea
a iˆ
x
a
y
ˆj
para os instantes dados e seus
1
0.5
0
-0.5
-1
2
1.5
1
22
0.5
0
-1
-0.5
0
0.5
1
Referências:
“Mecânica Vetorial para Engenheiros –
Estática”, Ferdinand P. Beer, E. Russell Johnston Jr.,
Makron Books.
Swokowski, V II.