RCL-kredsløb og Resonans

More documents

Recommendations

Info

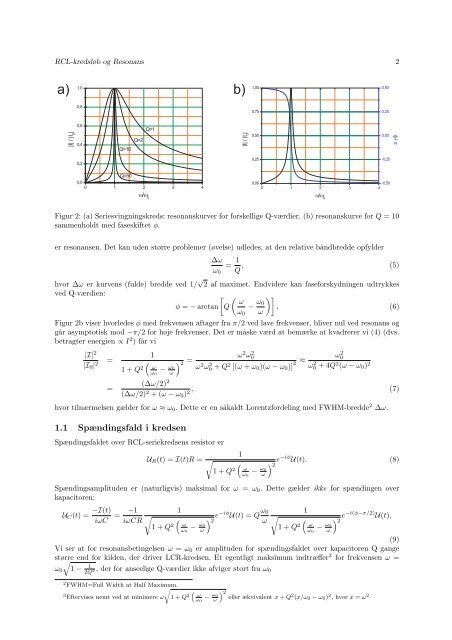
RCL-kredsløb og Resonans 2 Figur 2: (a) Seriesvingningskreds: resonanskurver for forskellige Q-værdier. (b) resonanskurve for Q = 10 sammenholdt med faseskiftet φ. er resonansen. Det kan uden større problemer (øvelse) udledes, at den relative b˚andbredde opfylder ∆ω ω0 = 1 , (5) Q hvor ∆ω er kurvens (fulde) bredde ved 1/ √ 2 af maximet. Endvidere kan faseforskydningen udtrykkes ved Q-værdien: � � ω φ = − arctan Q − ω0 ω0 �� . (6) ω Figur 2b viser hvorledes φ med frekvensen aftager fra π/2 ved lave frekvenser, bliver nul ved resonans og g˚ar asymptotisk mod −π/2 for høje frekvenser. Det er m˚aske værd at bemærke at kvadrerer vi (4) (dvs. betragter energien ∝ I2 ) f˚ar vi |I| 2 |I0| 2 = = 1 1 + Q2 � ω ω0 �2 = ω0 − ω ω2ω2 0 ω2ω2 0 + Q2 2 ≈ [(ω + ω0)(ω − ω0)] ω 2 0 ω 2 0 + 4Q2 (ω − ω0) 2 (∆ω/2) 2 (∆ω/2) 2 , (7) + (ω − ω0) 2 hvor tilnærmelsen gælder for ω ≈ ω0. Dette er en s˚akaldt Lorentzfordeling med FWHM-bredde 2 ∆ω. 1.1 Spændingsfald i kredsen Spændingsfaldet over RCL-seriekredsens resistor er UR(t) = I(t)R = � 1 + Q 2 1 � ω ω0 � e 2 ω0 − ω −iφ U(t). (8) Spændingsamplituden er (naturligvis) maksimal for ω = ω0. Dette gælder ikke for spændingen over kapacitoren: UC(t) = −I(t) iωC −1 1 = � iωCR 1 + Q2 � ω ω0 � e 2 ω0 − ω −iφ U(t) = Q ω0 ω � 1 + Q 2 1 � ω ω0 � e 2 ω0 − ω −i(φ−π/2) U(t). (9) Vi ser at for resonansbetingelsen ω = ω0 er amplituden for spændingsfaldet over kapacitoren Q gange større end for kilden, der driver LCR-kredsen. Et egentligt maksimum indtræffer3 � for frekvensen ω = ω0 1 − 1 2Q2 , der for anseelige Q-værdier ikke afviger stort fra ω0 2FWHM=Full Width at Half Maximum. � 3 Eftervises nemt ved at minimere ω 1 + Q 2 � ω ω0 �2 ω0 − eller ækvivalent x + Q ω 2 (x/ω0 − ω0) 2 , hvor x = ω2
RCL-kredsløb og Resonans 3 2 Parallelkreds Figur 1b viser en kapacitor C og en spole L kombineret i parallel. Da tr˚aden, som spolen er viklet af, har en endelig ledningsevne, har vi inkluderet en seriemodstand i spolens gren af netværket RL, som repræsenterer spolens ohmske modstand. Den komplekse erstatningsimpedans for denne kombination (jvf. figur) er ZCL = 1 1 ZC + 1 1 = −iωC + ZL+ZRL 1 −iωL+RL iQ − ω0/ω 1 + 2 = RL = RLQ ω/ω0 + i/Q − ω0/ω i Q � ω 1 − iQ iωL − RL = ω2 CL +iω CRL � �� (ω0Q) −1 � �� iω ω0L/RL −ω0 = RL −1 ω2 /ω0 + iω/Q − ω0 ω0 �� ω −2 0 ω0 ω − ω0 ω �, (10) � ZCL bliver reel n˚ar ω = ω0 1 − 1/Q2 . Vi noterer, at modulus for ZCL er |ZCL| = RLQ 2 � � � � 1 + � 1 Q2 ω2 0 ω2 1 + Q2 � �2 , (11) ω ω0 − ω0 ω som er maksimal for ω = ω0 � �1 + 2/Q 2 − 1/Q 2 . Havde vi haft en harmonisk variende strømkilde til vores r˚adighed og forbundet den til ZCL ville spændingsfaldet over impedansen alts˚a være maksimalt her 4 . I stedet skal vi kombinere ZCL i serie med en modstand R (se fig. 1b) Driver vi kredsløbet (p˚a indgangen) med en harmonisk varierende spænding Vin cos ωt vil amplituden for spændingen over ZCL være (generelt) VCL = |ZCL| |ZCL + R| Vin = RLQ 2 � � � � 1 + � 1 Q2 ω2 0 ω2 (R + Q2RL) 2 + Q2 � (RL + R) ω0 �2 Vin. (12) ω ω − R ω0 Det er værd at overveje den funktionelle opførsel for (12) i forskellige grænsetilfælde. Hvad sker der i grænsen, hvor R er stor (R ≫ |ZCL|)? — n˚ar Q er stor? — omkring ω0? I eksperimentet vil vi opbygge et kredsløb hvor RL ≪ R. I dette tilfælde er det nyttigt at definere en effektive Q-værdi Q ′ med Q ′ = Q 1 + Q2 , (13) RL/R som tillader os at approksimere spændingsamplitude over ZCL analogt til eq.(4) med standardform af nævneren: VCL = RL R QQ′ � � � � 1 + � 1 Q2 ω2 0 ω2 1 + Q ′2 � �2 , (14) ω ω0 − ω0 ω som viser at bredden af resonanskurven er bestemt af den effektive Q-værdi. 4 Dette er s˚aledes i modsætning til seriekredsen, hvor resonans optræder, n˚ar impedansen er minimal. Q
Page 1: Niels Bohr Institutet , November 12

RCL-kredsløb og Resonans

Create successful ePaper yourself

Delete template?

Save as template?