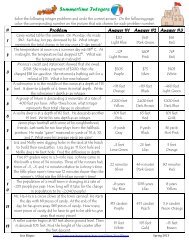
Conditional Statement Converse Inverse Contrapositive Hypothesis ...

. Multiple choice: If you learn a new mathematical result in the form “if p, then q,” what can you
immediately conclude, without any additional information, about the truth value of the contrapositive?
A) no conclusion because the contrapositive is not logically equivalent
B) conclude that the contrapositive is true
C) conclude that the contrapositive is false
Summarizing the information about forming related conditional statements, we see that the conditional “if p,
then q,” has three related conditional statements:
converse: “if q, then p” (swaps the hypothesis/conclusion)
inverse: “if not p, then not q” (negates the hypothesis/conclusion)
contrapositive: “if not q, then not p” (negates hypothesis/conclusion, then swaps)
Which, if any, of these is logically equivalent to the original conditional statement and always has the
same truth value as the original?
The absolute value function f and the functions g and h that you have worked with in this investigation are not
linear. However, in your study of functions prior to Mathematics I, you have worked with many linear
functions. We conclude this investigation with discussion about converse, inverse, and contrapositive using a
linear function.
11. Consider the linear function F which converts a temperature of c degrees Celsius to the equivalent
temperature of F(c) degrees Fahrenheit. The formula is given by
F(c) = 9
5 c + 32, where c is a temperature in degrees Celsius.
a. What is freezing cold in degrees Celsius? in degrees Fahrenheit? Verify that the formula for F
converts correctly for freezing temperatures.
b. What is boiling hot in degrees Celsius? in degrees Fahrenheit? Verify that the formula for F converts
correctly for boiling hot temperatures.
c. Draw the graph of F for values of c such that –100 ≤ c ≤ 400. What is the shape of the graph you
drew? Is this the shape of the whole graph?