Written Homework 7 Solutions
Written Homework 7 Solutions
Written Homework 7 Solutions
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
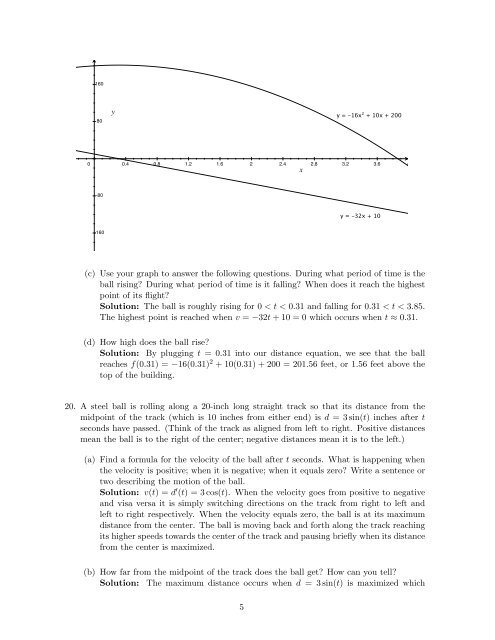
160<br />
80<br />
0 0.4 0.8 1.2 1.6 2 2.4 2.8 3.2 3.6 4<br />
-80<br />
-160<br />
y = -16x² + 10x + 200<br />
y = -32x + 10<br />
(c) Use your graph to answer the following questions. During what period of time is the<br />
ball rising? During what period of time is it falling? When does it reach the highest<br />
point of its flight?<br />
Solution: The ball is roughly rising for 0 < t < 0.31 and falling for 0.31 < t < 3.85.<br />
The highest point is reached when v = −32t + 10 = 0 which occurs when t ≈ 0.31.<br />
(d) How high does the ball rise?<br />
Solution: By plugging t = 0.31 into our distance equation, we see that the ball<br />
reaches f(0.31) = −16(0.31) 2 + 10(0.31) + 200 = 201.56 feet, or 1.56 feet above the<br />
top of the building.<br />
20. A steel ball is rolling along a 20-inch long straight track so that its distance from the<br />
midpoint of the track (which is 10 inches from either end) is d = 3 sin(t) inches after t<br />
seconds have passed. (Think of the track as aligned from left to right. Positive distances<br />
mean the ball is to the right of the center; negative distances mean it is to the left.)<br />
(a) Find a formula for the velocity of the ball after t seconds. What is happening when<br />
the velocity is positive; when it is negative; when it equals zero? Write a sentence or<br />
two describing the motion of the ball.<br />
Solution: v(t) = d ′ (t) = 3 cos(t). When the velocity goes from positive to negative<br />
and visa versa it is simply switching directions on the track from right to left and<br />
left to right respectively. When the velocity equals zero, the ball is at its maximum<br />
distance from the center. The ball is moving back and forth along the track reaching<br />
its higher speeds towards the center of the track and pausing briefly when its distance<br />
from the center is maximized.<br />
(b) How far from the midpoint of the track does the ball get? How can you tell?<br />
Solution: The maximum distance occurs when d = 3 sin(t) is maximized which<br />
5