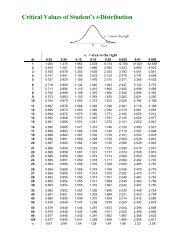
Circle Geometry - CEMC - University of Waterloo

Euclid eWorkshop #6
CIRCLE GEOMETRY
7. If ABCD is a quadrilateral with an inscribed circle as shown, prove that AB + CD = AD + BC.
D
A
B
C
8. In this diagram, the two circles are tangent at A. The line BDC is tangent to the smaller circle. Show that AD
bisects ∠BAC.
A
B
D
C
9. Starting at point A 1 on a circle, a particle moves to A 2 on the circle along chord A 1 A 2 which makes a clockwise
angle of 35 ◦ to the tangent to the circle at A 1 . From A 2 the particle moves to A 3 along chord A 2 A 3 which
makes a clockwise angle of 37 ◦ to the tangent at A 2 . The particle continues in this way. From A k it moves to
A k+1 along chord A k A k+1 which makes a clockwise angle of (33 + 2k) ◦ to the tangent to the circle at A k .
After several trips around the circle, the particle returns to A 1 for the first time along chord A n A 1 . Find the
value of n.
A 1
A 2
A 3
37 0
35 0 39 0
41 0 A 4
CANADIAN MATHEMATICS COMPETITION 6