OPPORTUNITIES IN NUCLEAR SCIENCE A Long-Range Plan for ...

THE SCIENCE • PROTONS AND NEUTRONS: STRUCTURE AND INTERACTIONS
R SM R EM
1
0
– 1
– 2
– 3
– 4
– 5
– 6
0
– 5
– 10
– 15
– 20
0
BATES
ELSA
LEGS
MAMI
MAMI
JLAB
JLAB
0.5 1 1.5 2 2.5 3 3.5 4
Q 2 [(GeV/c) 2 ]
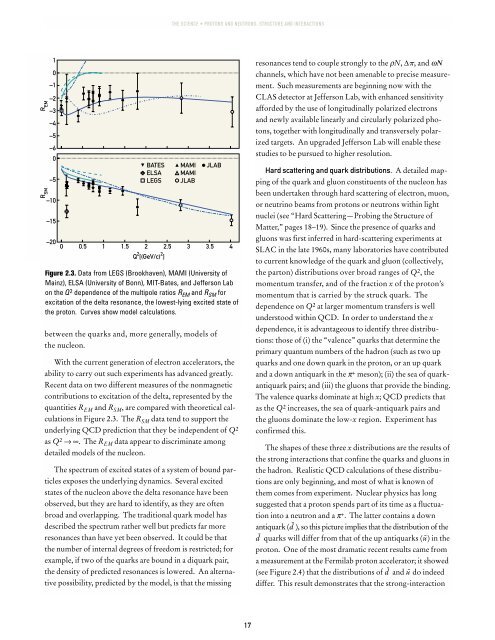
Figure 2.3. Data from LEGS (Brookhaven), MAMI (University of
Mainz), ELSA (University of Bonn), MIT-Bates, and Jefferson Lab
on the Q 2 dependence of the multipole ratios R EM and R SM for
excitation of the delta resonance, the lowest-lying excited state of
the proton. Curves show model calculations.
between the quarks and, more generally, models of
the nucleon.
With the current generation of electron accelerators, the
ability to carry out such experiments has advanced greatly.
Recent data on two different measures of the nonmagnetic
contributions to excitation of the delta, represented by the
quantities R EM and R SM , are compared with theoretical calculations
in Figure 2.3. The R SM data tend to support the
underlying QCD prediction that they be independent of Q 2
as Q 2 → ∞. The R EM data appear to discriminate among
detailed models of the nucleon.
The spectrum of excited states of a system of bound particles
exposes the underlying dynamics. Several excited
states of the nucleon above the delta resonance have been
observed, but they are hard to identify, as they are often
broad and overlapping. The traditional quark model has
described the spectrum rather well but predicts far more
resonances than have yet been observed. It could be that
the number of internal degrees of freedom is restricted; for
example, if two of the quarks are bound in a diquark pair,
the density of predicted resonances is lowered. An alternative
possibility, predicted by the model, is that the missing
resonances tend to couple strongly to the ρN, ∆, and ωΝ
channels, which have not been amenable to precise measurement.
Such measurements are beginning now with the
CLAS detector at Jefferson Lab, with enhanced sensitivity
afforded by the use of longitudinally polarized electrons
and newly available linearly and circularly polarized photons,
together with longitudinally and transversely polarized
targets. An upgraded Jefferson Lab will enable these
studies to be pursued to higher resolution.
Hard scattering and quark distributions. A detailed mapping
of the quark and gluon constituents of the nucleon has
been undertaken through hard scattering of electron, muon,
or neutrino beams from protons or neutrons within light
nuclei (see “Hard Scattering—Probing the Structure of
Matter,” pages 18–19). Since the presence of quarks and
gluons was first inferred in hard-scattering experiments at
SLAC in the late 1960s, many laboratories have contributed
to current knowledge of the quark and gluon (collectively,
the parton) distributions over broad ranges of Q 2 , the
momentum transfer, and of the fraction x of the proton’s
momentum that is carried by the struck quark. The
dependence on Q 2 at larger momentum transfers is well
understood within QCD. In order to understand the x
dependence, it is advantageous to identify three distributions:
those of (i) the “valence” quarks that determine the
primary quantum numbers of the hadron (such as two up
quarks and one down quark in the proton, or an up quark
and a down antiquark in the π + meson); (ii) the sea of quarkantiquark
pairs; and (iii) the gluons that provide the binding.
The valence quarks dominate at high x; QCD predicts that
as the Q 2 increases, the sea of quark-antiquark pairs and
the gluons dominate the low-x region. Experiment has
confirmed this.
The shapes of these three x distributions are the results of
the strong interactions that confine the quarks and gluons in
the hadron. Realistic QCD calculations of these distributions
are only beginning, and most of what is known of
them comes from experiment. Nuclear physics has long
suggested that a proton spends part of its time as a fluctuation
into a neutron and a π + . The latter contains a down
antiquark (d - ), so this picture implies that the distribution of the
d - quarks will differ from that of the up antiquarks (ū) in the
proton. One of the most dramatic recent results came from
a measurement at the Fermilab proton accelerator; it showed
(see Figure 2.4) that the distributions of d - and ū do indeed
differ. This result demonstrates that the strong-interaction
17