Sborník vědeckých prací Vysoké školy báňské ... - Transactions

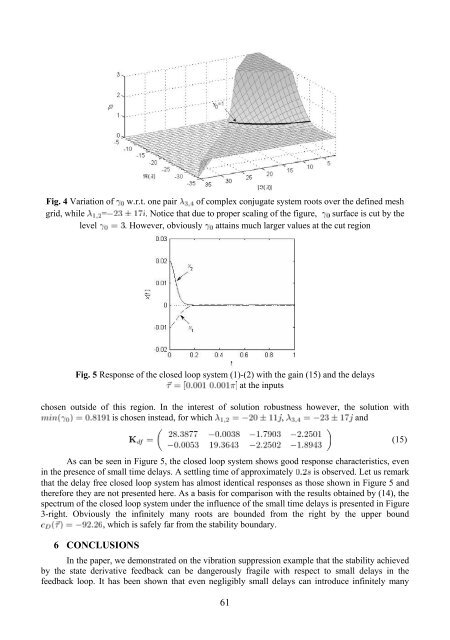
Fig. 4 Variation of w.r.t. one pair of complex conjugate system roots over the defined mesh
grid, while = . Notice that due to proper scaling of the figure, surface is cut by the
level . However, obviously attains much larger values at the cut region
Fig. 5 Response of the closed loop system (1)-(2) with the gain (15) and the delays
at the inputs
chosen outside of this region. In the interest of solution robustness however, the solution with
is chosen instead, for which , and
As can be seen in Figure 5, the closed loop system shows good response characteristics, even
in the presence of small time delays. A settling time of approximately is observed. Let us remark
that the delay free closed loop system has almost identical responses as those shown in Figure 5 and
therefore they are not presented here. As a basis for comparison with the results obtained by (14), the
spectrum of the closed loop system under the influence of the small time delays is presented in Figure
3-right. Obviously the infinitely many roots are bounded from the right by the upper bound
, which is safely far from the stability boundary.
6 CONCLUSIONS
In the paper, we demonstrated on the vibration suppression example that the stability achieved
by the state derivative feedback can be dangerously fragile with respect to small delays in the
feedback loop. It has been shown that even negligibly small delays can introduce infinitely many
61
(15)