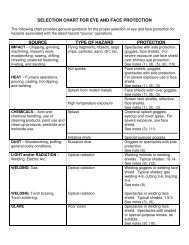
Three Dimensional Coordinate System. Functions of Two Variables ...

If the equation F (x, y, z) = 0 can be solved for z, for example, the solution
z = f(x, y)
represent the explicit form of function F.
Examples.
1. Line in two dimensions Plane in three dimensions
ax + by = c
ax + by + cz = d
2. Circle in two dimensions Sphere in three dimensions
Center: (a, b), radius: r. Center: (a, b, c), radius: r.
(x − a) 2 + (y − b) 2 = r 2 (x − a) 2 + (y − b) 2 + (z − c) 2 = r 2
Figure 2: Sphere (x − a) 2 + (y − b) 2 + (z − c) 2 = r 2
The formula for circle/sphere follows from the formula for the distance:
The distance between the points The distance between the points
P (x 1 , y 1 ) and Q(x 2 , y 2 ) P (x 1 , y 1 , z 1 ) and Q(x 2 , y 2 , z 2 )
|P Q| =
√
√
(x 1 − x 2 ) 2 + (y 1 − y 2 ) 2 |P Q| = (x 1 − x 2 ) 2 + (y 1 − y 2 ) 2 + (z 1 − z 2 ) 2
The equation of this circle in three dimensions is obtained from the formula that describes all
points (x, y, z) with the distance r from the point (a, b, c) :
Distance =
Examples (continued).
√
(x − a) 2 + (y − b) 2 + (z − c) 2 = r ⇒ (x − a) 2 + (y − b) 2 + (z − c) 2 = r 2 .
3. Cylindrical surfaces – one variable not present in the equation. For example, z = f(y). To
graph this surface, graph the function z = f(y) in yz-plane and translate the graph in direction
of x-axis. For example,
– The graph of x 2 + y 2 = 4 is the cylinder obtained by translating the circle x 2 + y 2 = 4
of radius 2 centered at the origin in xy-plane along z-axis.