Nonlinear bending and stretching of a circular graphene sheet ...

More documents

Recommendations

Info

Nanotechnology 20 (2009) 075702W H Duan and C M Wangbe scaled to W 0 /P ∝ 1/λ 2 . As for the transition between plateand membrane behavior in the range of 0.5 < λ < 1, thecentral deflection is given byW 0P = 1 ( 12πλ 2 λI 1 (λ) [1 − I 0(λ)][1 − λK 1 (λ)])+ K 0 (λ) + ln(λ/2) + γ , (11)where the Euler’s constant γ is approximately 0.5772, and itsanalytical expression is given by( ∑)1γ = limn→∞ i − ln n . (12)i=1···n3.3. Slope and curvature variations near the central regionand edge zoneIn section 3.2, it is concluded that stretching generallydominates the graphene sheet deflection. In this section, wewill explore the bending effect in the central region and edgezone. Figure 4 shows the variation of the slope with respectto the non-dimensional radius η for λ = 15.94 based on MMsimulations. Interestingly, the results from the MM simulationsshow that the slope of the graphene sheet has a singularityin the vicinity of the central point. The graphene sheetbehaves nonlinearly in this vicinity, whereas it behaves linearlyelastically further away from the central region, as shown insection 3.2. Owing to the discrete distribution of carbon atomsin the graphene sheet, the sharp variation of the slope aroundcentral region is difficult to show by MM simulations. Again,we can use the Kirchhoff plate theory to examine the slope andcurvature variations near the central region and edge zone as itcan be treated analytically.We first introduce the large value approximation for themodified Bessel functions, namely [32]lim I β(x) = √ ex, andx→∞ 2πx√ πlim K β(x) = e −xx→∞ 2x . (13)Based on this approximation, equation (9) furnishes, for largeλ,θ(η) =P ( √e −λη λπ2πλ 2 2η + e−λ(1−η)√ − 1 ). (14)η ηThis equation indicates √ a small exponential central region(corresponding to e −λη λπ) and edge (corresponding to2ηe −λ(1−η)√ η) corrections to the pure membrane case to accommodatethe zero slope condition at η = 0 and 1. This results in largecurvature changes which can be explained from equation (10).For large λ, the maximum curvature term at the edge isobtained as ϕ(1) = P/(2πλ), while the curvature term ϕ(0)approaches infinity due to the ln(λη/2) term in equation (10).These two values are considerably greater than the membranecurvature ϕ(η) = P/(2πλ 2 ) at the middle portion of thecircular graphene sheet. Physically, this indicates the presenceof a stress concentration in the central region and the edgezone. In order to reduce the stress concentration, the substrateFigure 4. Slope variation in the central region and edge zone for acircular graphene sheet with 4 nm radius: the initial in-plane tensionis set to be λ = 15.94; the corresponding initial length of the carbonbond is 0.0140 nm.supporting the graphene sheet should be as thin as possible aswell as relatively softer, so that the boundary condition canbe simulated as a simply supported edge. The curvature of acircular graphene sheet for the simply supported edge is givenbyϕ(η) = P2π( 1λ 2 η − K 0(λη) − K 1(λη)2 λη− (1 − ν)(1 − λK 1(λ)) − λ 2 K 0 (λ)λ[λI 0 (λ)−(1−ν)I 1 (λ)](I 0 (λη)− I ))1(λη).λη(15)By using a similar analysis for the clamped graphene sheet, onecan obtain ϕ(1) = ν P/(2πλ 2 ), which has the same scale forin-plane tension λ, at the middle part of the circular graphenesheet. Therefore the stress concentration may be reduced oravoided. As for the stress concentration near the central point,it can be easily reduced by spreading the area of the loadapplication.4. Assessment of continuum mechanics model for theanalysis of graphene sheetsThe analysis in section 3 shows that the von Kármán platetheory is able to furnish results that are in reasonable agreementwith MM simulation results. Although it still needs somenumerical computations, it is faster than performing MMsimulations. Kirchhoff’s theory can be used as a quick andrough approximation, particularly for small deflections, asthey can be treated analytically. In order to quantitativelydemonstrate the accuracy of the continuum mechanics modelfor the analysis of graphene sheets, the point load P values fora given central deflection value W 0 for graphene sheets with4 nm radius and 10 nm radius obtained from MM simulationsare compared to the Kirchhoff plate and the von Kármán plateresults in table 1. It can be seen that, for small deflections, theresults from the Kirchhoff plate theory and the von Kármánplate theory are in close agreement with the MM results. For5
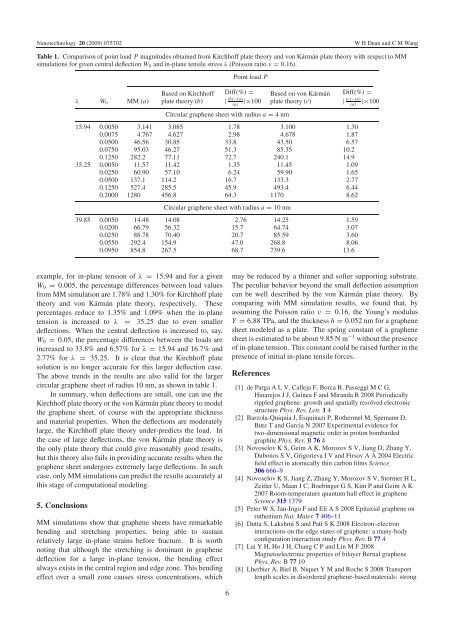
Nanotechnology 20 (2009) 075702W H Duan and C M WangTable 1. Comparison of point load P magnitudes obtained from Kirchhoff plate theory and von Kármán plate theory with respect to MMsimulations for given central deflection W 0 and in-plane tensile stress λ (Poisson ratio ν = 0.16).λ W 0 MM (a)Based on Kirchhoffplate theory (b)Point load PDiff(%) =| (b)−(a)(a)|×100Circular graphene sheet with radius a = 4nmBasedonvonKármánplate theory (c)15.94 0.0050 3.141 3.085 1.78 3.100 1.300.0075 4.767 4.627 2.98 4.678 1.870.0500 46.56 30.85 33.8 43.50 6.570.0750 95.03 46.27 51.3 85.35 10.20.1250 282.2 77.11 72.7 240.1 14.935.25 0.0050 11.57 11.42 1.35 11.45 1.090.0250 60.90 57.10 6.24 59.90 1.650.0500 137.1 114.2 16.7 133.3 2.770.1250 527.4 285.5 45.9 493.4 6.440.2000 1280 456.8 64.3 1170 8.62Circular graphene sheet with radius a = 10 nm39.85 0.0050 14.48 14.08 2.76 14.25 1.590.0200 66.79 56.32 15.7 64.74 3.070.0250 88.78 70.40 20.7 85.59 3.600.0550 292.4 154.9 47.0 268.8 8.060.0950 854.8 267.5 68.7 739.6 13.6Diff(%) =| (c)−(a)(a)|×100example, for in-plane tension of λ = 15.94 and for a givenW 0 = 0.005, the percentage differences between load valuesfrom MM simulation are 1.78% and 1.30% for Kirchhoff platetheory and von Kármán plate theory, respectively. Thesepercentages reduce to 1.35% and 1.09% when the in-planetension is increased to λ = 35.25 due to even smallerdeflections. When the central deflection is increased to, say,W 0 = 0.05, the percentage differences between the loads areincreased to 33.8% and 6.57% for λ = 15.94 and 16.7% and2.77% for λ = 35.25. It is clear that the Kirchhoff platesolution is no longer accurate for this larger deflection case.The above trends in the results are also valid for the largercircular graphene sheet of radius 10 nm, as shown in table 1.In summary, when deflections are small, one can use theKirchhoff plate theory or the von Kármán plate theory to modelthe graphene sheet, of course with the appropriate thicknessand material properties. When the deflections are moderatelylarge, the Kirchhoff plate theory under-predicts the load. Inthe case of large deflections, the von Kármán plate theory isthe only plate theory that could give reasonably good results,but this theory also fails in providing accurate results when thegraphene sheet undergoes extremely large deflections. In suchcase, only MM simulations can predict the results accurately atthis stage of computational modeling.5. ConclusionsMM simulations show that graphene sheets have remarkablebending and stretching properties, being able to sustainrelatively large in-plane strains before fracture. It is worthnoting that although the stretching is dominant in graphenedeflection for a large in-plane tension, the bending effectalways exists in the central region and edge zone. This bendingeffect over a small zone causes stress concentrations, whichmay be reduced by a thinner and softer supporting substrate.The peculiar behavior beyond the small deflection assumptioncan be well described by the von Kármán plate theory. Bycomparing with MM simulation results, we found that, byassuming the Poisson ratio ν = 0.16, the Young’s modulusY = 6.88 TPa, and the thickness h = 0.052 nm for a graphenesheet modeled as a plate. The spring constant of a graphenesheet is estimated to be about 9.85 N m −1 without the presenceof in-plane tension. This constant could be raised further in thepresence of initial in-plane tensile forces.References[1] de Parga A L V, Calleja F, Borca B, Passeggi M C G,Hinarejos J J, Guinea F and Miranda R 2008 Periodicallyrippled graphene: growth and spatially resolved electronicstructure Phys. Rev. Lett. 1 4[2] Barzola-Quiquia J, Esquinazi P, Rothermel M, Spemann D,Butz T and Garcia N 2007 Experimental evidence fortwo-dimensional magnetic order in proton bombardedgraphite Phys. Rev. B 76 4[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y,Dubonos S V, Grigorieva I V and Firsov A A 2004 Electricfield effect in atomically thin carbon films Science306 666–9[4] Novoselov K S, Jiang Z, Zhang Y, Morozov S V, Stormer H L,Zeitler U, Maan J C, Boebinger G S, Kim P and Geim A K2007 Room-temperature quantum hall effect in grapheneScience 315 1379[5] Peter W S, Jan-Ingo F and Eli A S 2008 Epitaxial graphene onruthenium Nat. Mater. 7 406–11[6] Dutta S, Lakshmi S and Pati S K 2008 Electron–electroninteractions on the edge states of graphene: a many-bodyconfiguration interaction study Phys. Rev. B 77 4[7] Lai Y H, Ho J H, Chang C P and Lin M F 2008Magnetoelectronic properties of bilayer Bernal graphenePhys. Rev. B 77 10[8] Lherbier A, Biel B, Niquet Y M and Roche S 2008 Transportlength scales in disordered graphene-based materials: strong6
Page 1: Home Search Collections Journals Ab

Nonlinear bending and stretching of a circular graphene sheet ...

Create successful ePaper yourself

Delete template?

Save as template?