computing the quartet distance between general trees

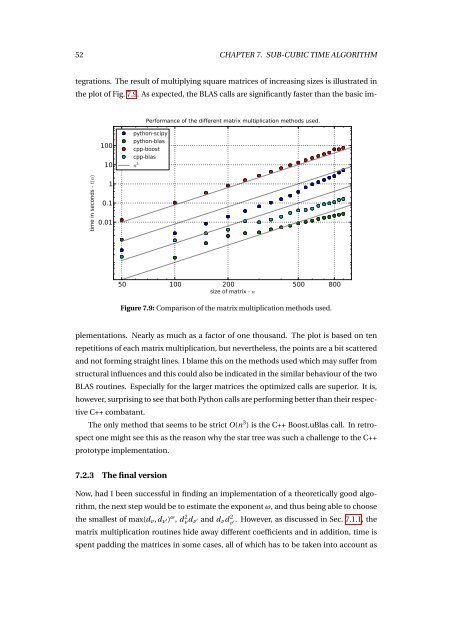
52 CHAPTER 7. SUB-CUBIC TIME ALGORITHMtegrations. The result of multiplying square matrices of increasing sizes is illustrated inthe plot of Fig. 7.9. As expected, the BLAS calls are significantly faster than the basic im-Performance of the different matrix multiplication methods used.10010python-scipypython-blascpp-boostcpp-blasn 3time in seconds - t(n)10.10.0150 100 200 500 800size of matrix - nFigure 7.9: Comparison of the matrix multiplication methods used.plementations. Nearly as much as a factor of one thousand. The plot is based on tenrepetitions of each matrix multiplication, but nevertheless, the points are a bit scatteredand not forming straight lines. I blame this on the methods used which may suffer fromstructural influences and this could also be indicated in the similar behaviour of the twoBLAS routines. Especially for the larger matrices the optimized calls are superior. It is,however, surprising to see that both Python calls are performing better than their respectiveC++ combatant.The only method that seems to be strict O(n 3 ) is the C++ Boost.uBlas call. In retrospectone might see this as the reason why the star tree was such a challenge to the C++prototype implementation.7.2.3 The final versionNow, had I been successful in finding an implementation of a theoretically good algorithm,the next step would be to estimate the exponent ω, and thus being able to choosethe smallest of max(d v ,d v ′) ω , dv 2d v ′ and d v d 2 . However, as discussed in Sec. 7.1.1, thev ′matrix multiplication routines hide away different coefficients and in addition, time isspent padding the matrices in some cases, all of which has to be taken into account as