Chapter 3 Acceleration and free fall - Light and Matter

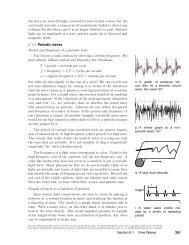
e / A coin slides across a table.
Even for motion in one
dimension, some of the forces
may not lie along the line of the
motion.
f / A simple double-pan balance
works by comparing the
weight forces exerted by the
earth on the contents of the two
pans. Since the two pans are
at almost the same location on
the earth’s surface, the value
of g is essentially the same for
each one, and equality of weight
therefore also implies equality of
mass.
g / Example 9.
134 Chapter 4 Force and motion
A coin sliding across a table example 8
Suppose a coin is sliding to the right across a table, e, and let’s
choose a positive x axis that points to the right. The coin’s velocity
is positive, and we expect based on experience that it will slow
down, i.e., its acceleration should be negative.
Although the coin’s motion is purely horizontal, it feels both vertical
and horizontal forces. The Earth exerts a downward gravitational
force F2 on it, and the table makes an upward force F3
that prevents the coin from sinking into the wood. In fact, without
these vertical forces the horizontal frictional force wouldn’t exist:
surfaces don’t exert friction against one another unless they are
being pressed together.
Although F2 and F3 contribute to the physics, they do so only
indirectly. The only thing that directly relates to the acceleration
along the horizontal direction is the horizontal force: a = F1/m.
The relationship between mass and weight
Mass is different from weight, but they’re related. An apple’s
mass tells us how hard it is to change its motion. Its weight measures
the strength of the gravitational attraction between the apple and
the planet earth. The apple’s weight is less on the moon, but its
mass is the same. Astronauts assembling the International Space
Station in zero gravity cannot just pitch massive modules back and
forth with their bare hands; the modules are weightless, but not
massless.
We have already seen the experimental evidence that when weight
(the force of the earth’s gravity) is the only force acting on an object,
its acceleration equals the constant g, and g depends on where
you are on the surface of the earth, but not on the mass of the object.
Applying Newton’s second law then allows us to calculate the
magnitude of the gravitational force on any object in terms of its
mass:
|FW | = mg .
(The equation only gives the magnitude, i.e. the absolute value, of
FW , because we’re defining g as a positive number, so it equals the
absolute value of a falling object’s acceleration.)
⊲ Solved problem: Decelerating a car page 152, problem 1
Weight and mass example 9
⊲ Figure g shows masses of one and two kilograms hung from a
spring scale, which measures force in units of newtons. Explain
the readings.
⊲ Let’s start with the single kilogram. It’s not accelerating, so
evidently the total force on it is zero: the spring scale’s upward
force on it is canceling out the earth’s downward gravitational
force. The spring scale tells us how much force it is being obliged