a

OPERACIONES CON INFINITOS E INFINITÉSIMOS.
En el cálculo directo de límites aparecen expresiones que tienden a infinito y otras que
tienden a cero (infinitésimos).
Al operar con ellas es posible que pueda obtenerse el resultado o que no pueda saberse de
forma inmediata y haya que realizar cierto número de operaciones para ello
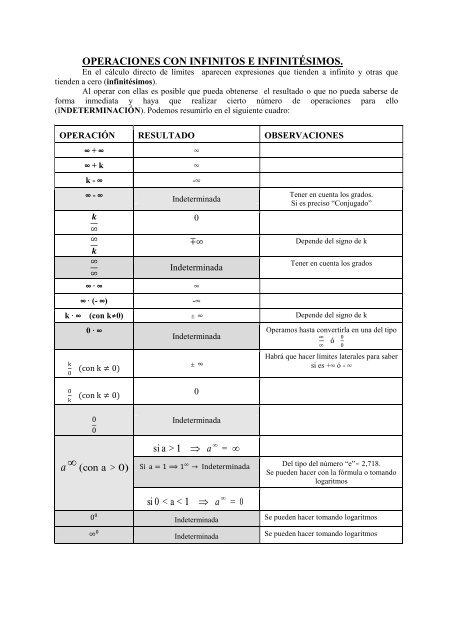
(INDETERMINACIÓN). Podemos resumirlo en el siguiente cuadro:
OPERACIÓN RESULTADO OBSERVACIONES
+
+ k
k - -
-
Indeterminada
Tener en cuenta los grados.
Si es preciso “Conjugado”
k
∞ 0
∞
k ∓∞ Depende del signo de k
∞
∞ Indeterminada Tener en cuenta los grados
(- ) -
k (con k0) Depende del signo de k
k
0
0
(con k ≠ 0)
Indeterminada
Operamos hasta convertirla en una del tipo
∞
ó 0
∞ 0
Habrá que hacer límites laterales para saber
si es + ó -
0
k
(con k ≠ 0)
0
0
0
Indeterminada
a (con a > 0)
si a > 1 a =
Si a = 1 ⟹ 1 ∞ → Indeterminada Del tipo del número “e” 2,718.
Se pueden hacer con la fórmula o tomando
logaritmos
si 0 < a < 1 a
= 0
0 0 Indeterminada Se pueden hacer tomando logaritmos
∞ 0 Indeterminada Se pueden hacer tomando logaritmos

GRADOS DE INFINITOS.
Resulta muy útil para comparar unos infinitos con otros y despreciar los que son de menor grado
Si suponemos que ( x ; a>1 , n>0 ) y ordenados de mayor a menor:
x x x
n
>> x ! >> a >> x > ln x
INFINITÉSIMOS EQUIVALENTES.
Expresiones que tienden a cero “infinitésimos” se pueden sustituir por otras más sencillas
que permitan simplificar el cálculo y resolución de indeterminaciones.
Para u → 0
Para u → 1
sen u ≈ u
tan u ≈ u
Arc sen u ≈ u
Arcu
cos u ≈ 1 − u2
2
e u ≈ 1 + u
≈ u − u3
6 + ⋯
≈ u + u3
3 + ⋯
≈ u + u3
6 + 3u5
40 + ⋯
≈ 1 − u2
2 + u4
24 − ⋯
≈ 1 + u + u2
2 + ⋯ ln u ≈ u − 1
a u ≈ 1 + u ln a
Como curiosidad estas equivalencias se obtienen mediante del Desarrollo en Serie de Taylor que
verás en cursos universitarios y que sirve para aproximar una función continua y derivable en un en
un entorno del punto x=a por un polinomio. La aproximación será tanto mejor cuanto más cerca
estemos del punto x=a.
f x ≈ f a + 1 1! f′ a x − a + 1 2! f´´ a (x − a)2 + 1 3! f´´´ a (x − a)3 + ⋯ . . … …
Si te apetece puedes comprobarlo desarrollando: y= sen x ó
REGLA DE L’HÔPITAL.
y=e x , por ejemplo, en el punto a=0.
Es una regla que permite utilizar las derivadas para calcular algunos límites que estén expresados en
forma de cociente y bajo determinadas condiciones.
lim
Si
x → a f x = 0 y lim
x → a g x = 0 o también
Si
lim
x → a f x = ∞ y lim
x → a g x = ∞
Se tiene que:
lim
x → a
f x
g x
=
lim
x → a
f´(x)
g´(x)
Es decir, se puede utilizar en indeterminaciones de los tipos:
0
0
ó
∞
∞
Ésta regla es válida cuando “a” es un número real, pero también cuando es +∞ ó − ∞