Machine de Turing et fonction récursive - Free
Machine de Turing et fonction récursive - Free
Machine de Turing et fonction récursive - Free
- No tags were found...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Théorème : Soit N k N une <strong>fonction</strong> calculée par une machine à registre R.<br />
Il existe une machine <strong>de</strong> <strong>Turing</strong> qui calcule <br />
Conséquence : L'ensemble <strong>de</strong>s <strong>fonction</strong>s calculables par les machines à Registres est inclus dans<br />
l'ensemble <strong>de</strong>s <strong>fonction</strong>s calculables par les machines <strong>de</strong> <strong>Turing</strong>.<br />
F*^k<br />
F*^MR<br />
<br />
F*^MT<br />
<strong>Machine</strong> <strong>de</strong> <strong>Turing</strong> <strong>et</strong> <strong>fonction</strong> récursive<br />
En gros : On compile les machines <strong>de</strong> <strong>Turing</strong>. On obtient sur le disque dur un nombre. Savoir<br />
manipuler les nombres <br />
A) Appariement : Nombre <strong>de</strong> Gö<strong>de</strong>l<br />
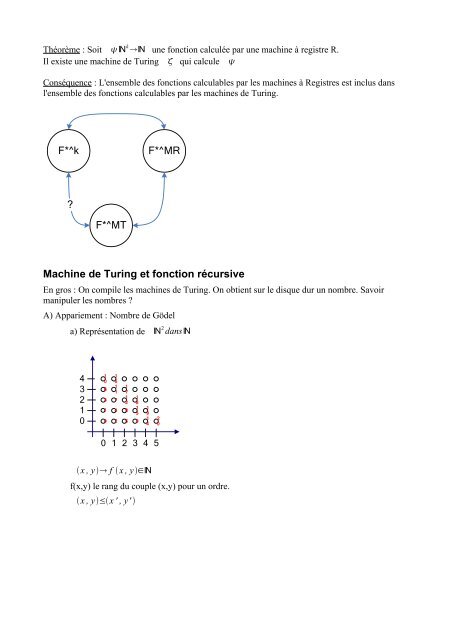
a) Représentation <strong>de</strong> N 2 dansN<br />
4<br />
3<br />
2<br />
1<br />
0<br />
1<br />
0<br />
6<br />
3<br />
1<br />
0<br />
1<br />
6<br />
1<br />
1<br />
7<br />
4<br />
2<br />
1<br />
7<br />
1<br />
2<br />
8<br />
5<br />
1<br />
8<br />
1<br />
3<br />
9<br />
1<br />
9<br />
1<br />
4<br />
2<br />
0<br />
0 1 2 3 4 5<br />
x , y f x , y∈N<br />
f(x,y) le rang du couple (x,y) pour un ordre.<br />
x , y≤x ' , y'
_\<br />
y’<br />
x’<br />
y− y'<br />
x−x ' =−1<br />
x−x ' y− y ' =0<br />
f x , y =<br />
f est élémentaire<br />
N 2 f<br />
N<br />
f x , y =<br />
N g ,h N<br />
g f x , y=x<br />
h f x , y = y<br />
f est une bijection<br />
x y x y 1<br />
x<br />
2<br />
x y x y 1<br />
x<br />
2<br />
f , g , h sont élémentaires<br />
g z≤ z ;h z≤z<br />
b) Représentation <strong>de</strong> N k N<br />
k=1 x id x<br />
k=2 x , y f f x , y <br />
k>2 :<br />
x 1 , ..., x k = f ... f f f x 1, x 2 , x 3 , x 4 ... , x k ∈N<br />
/*...<br />
Ces <strong>fonction</strong>s se calculent en temps polynomial<br />
Compilation <strong>de</strong>s machines <strong>de</strong> <strong>Turing</strong> :<br />
A ∞ ={a 0,<br />
a 1...<br />
}∞ dénombrable<br />
a 0 représente 0<br />
a 1 représente 1<br />
Q ∞ ={q 0,<br />
q 1.......<br />
}∞ dénombrable pour les états
A ∞ ∩Q ∞ =0<br />
S ∞ =A ∞ ∪Q ∞ ∪{¤ , R , L , N }<br />
Codage : cd n'utilise que les nombres impaires<br />
SCHEMA 4<br />
cd (arbitraire) co<strong>de</strong> tous les symboles d'une MT<br />
Etat x=∃ i≤ x<br />
x=94i<br />
L<strong>et</strong>trex=∃ i≤ x<br />
x=74i<br />
Deplacement x=x=1∨x=3∨ x=4<br />
∗<br />
w ∈S ∞<br />
[w]= 0 si w=<br />
[[cd w 1<br />
,........ cd w k<br />
]] si w=w 1<br />
....... w k<br />
w i<br />
∈S ∞<br />
[[a 2<br />
q 1<br />
a 3<br />
a 1<br />
]] = 88887111659994600815<br />
transciente*/<br />
Théorème : Les <strong>fonction</strong>s calculables par une MT sont <strong>de</strong>s <strong>fonction</strong>s récursives<br />
F*^k<br />
F*^MR<br />
<br />
F*^MT<br />
Thèse <strong>de</strong> Church :<br />
Dire qu'une <strong>fonction</strong> est calculable c'est dire qu'elle est récursive. Ne dépend pas <strong>de</strong> la technique.<br />
Théorème : (forme normale)<br />
Pour tout k, il existe un prédicat élémentaire C k <strong>et</strong> une <strong>fonction</strong> élémentaire V tel que pour toute<br />
<strong>fonction</strong> récursive N k N , il existe un entier z∈N tel que<br />
∀ x 1, .... , x k x 1 ..... x k =V y C k x 1 .... x k , y , z<br />
∀ ∈F k R ∃ z∈N<br />
= y z<br />
k<br />
(z est un nombre <strong>de</strong> Gö<strong>de</strong>l <strong>de</strong> )