Geodesia - Dipartimento di Ingegneria Civile

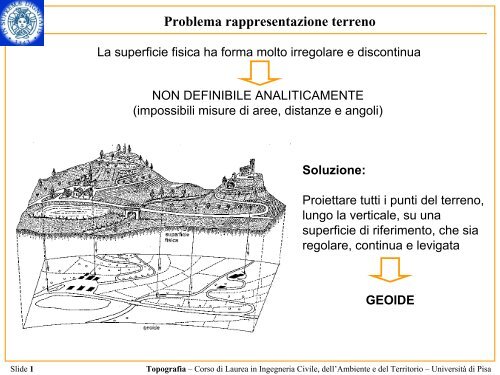
Problema rappresentazione terrenoLa superficie fisica ha forma molto irregolare e discontinuaNON DEFINIBILE ANALITICAMENTE(impossibili misure di aree, distanze e angoli)Soluzione:Proiettare tutti i punti del terreno,lungo la verticale, su unasuperficie di riferimento, che siaregolare, continua e levigataGEOIDESlide 1Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Procedura di rilievo e rappresentazionePer ottenere il rilievo e la rappresentazione della superficie fisicaterrestre occorre:- Definire l’equazione del geoide- Definire il sistema di coordinate curvilinee u, v- Definire angoli e distanze sul geoide- Definire la trasformazione delle misure di angoli e distanze in u,v- Definire la trasformazione da u,v in coordinate pianeSlide 4Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

GeodesiaCompiti della GEODESIA sono:- Definizione del geoide nella sua forma e nelle sue dimensioni- Definizione del campo gravitazionale terrestre in ogni punto(intensità e direzione del vettore di gravità g r )- Ipotesi e conclusioni generali relative alla distribuzione internadelle masse nel globo terrestreGeodesia geometrica → assume il fatto che il geoide possa esseresemplificato con una superficie algebrica precisa (sfera, ellissoide dirotazione), studia la geometria delle superfici e insegna a sviluppare letriangolazioni e calcolare le relazioni di posizione fra i suoi puntiGeodesia dinamica → definisce il geoide come una superficieequipotenziale del campo gravitazionale, ne studia lo scostamento dallesuperfici geometriche ed insegna a tenere conto delle conseguenzeoperativeSlide 5Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoIl geoide è la supeficie normale in ogni punto alla direzione della verticaleLa gravità costituisce un campo di forza conservativo → ammette potenzialeLinee di forza→ linee tangenti in ogni punto alla direzione della gravità→ curve gobbe (non appartenenti ad un piano)Superfici equipotenziali → infinite e normali alle linee di forza del campoIl geoide è una superficie equipotenziale della gravità, che passa perun determinato punto cui viene attribuita quota nulla. Questo punto èdefinito in modo assoluto da un mareografo.Slide 6Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoCome noto:rg=grad W∂W∂X=rgX∂W∂Y=rgY∂W∂Z=rgZSe indichiamo con dP uno spostamentoinfinitesimo del punto P, vale la relazione:dW gr r= ⋅ PdPOssia, la derivata del potenziale secondo una direzione dP fornisce lacomponente del vettore gravità in quella direzioneSe lo spostamento dP è tangente alla superficie r requipotenziale passante per P, risulta: dW = g P⋅dP= 0Da cui si deduce l’ortogonalità di g r rispetto alla superficie equipotenzialeSia W che le sue derivate prime sono funzioni continue e prive disingolarità, per cui le superfici equipotenziali sono lisce e prive di spigoli opunti singolari → In ogni punto esiste una sola normale superficialeunivocamente definita e variabile con continuitàCiò nonostante la superficie presenta continue gibbositàSlide 8Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoIl potenziale W è una quantità scalare ed è pari alla somma dei potenzialidella forza di attrazione universale F re della forza centifuga c rPotenziale FORZA CENTRIFUGAPer ricavare il potenziale della forza centrifuga ricordiamo che la derivatadel potenziale secondo una direzione fornisce la componente della forzain quella direzionedv r= c = ω2 ⋅rdrIl potenziale sarà dunque:v(X,Y) = ∫ ω2⋅rdr=1ω22⋅r2=1ω22⋅(X2+Y2)Slide 9Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoRicordando la relazione esistente tra potenziale e forza si può scrivere:∂dV∂l=dF→dV=G ⋅ dml∫dF⋅ dl = ∫ dl =2GdmlE quindi il potenziale dovuto a tutta la massa della terra:V(X,Y,Z)=G ⋅∫∫∫VTERRAdmlIl potenziale W risulta dalla somma del potenziale V, relativo alla forza diattrazione gravitazionale e dal potenziale v relativo alla forza centrifuga(i potenziali possono essere sommati perchè sono funzioni scalari)Se poniamo W = cost :V(X, Y,Z) + v(X,Y) = costFamiglia di superficiequipotenzialiSlide 11Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoX = σ ·cosψ · cos λY = σ · cos ψ · sin λZ = σ · sin ψDopo lo sviluppo in serie, limitato ai termini di secondo grado, avremo:V = V’ + T, dove T indica il potenziale residuo di grado ≥ 3.Il potenziale della gravità diventa quindi:W = V + vW = V’ + v + TW = U + TU → Potenziale normaleT → Potenziale anomaloSlide 14Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoAl potenziale normale U corrisponde una forza γ, definita gravità normaleLa differenza tra il modulo dei due vettori g r (gravità) e γ r (gravità normale), sichiama ANOMALIA di gravità e oggi è la grandezza più diffusamente misurataper il calcolo del geoide.Dopo aver sostituito le coordinate geocentriche con le coordinate polari σ, ψ, λ,a meno di termini dell’ordine di 1/ σ 4 (σ≈6370 km e 1/ σ 4 ≈ 6.07· 10 -28 ), ilpotenziale V’ risulta espresso dalla seguente relazione approssimata:G ⋅M⎡ 1 ⎛ A + B ⎞3 B − AV'( σ,ψ,λ)= ⋅⎢1+⋅⎜C− ⎟ ⋅cos2λ22σ ⎣ 2 ⋅σ⋅M⎝ 2 ⎠4 ⋅σM22 ⎤( 1−3 ⋅sinψ) + ⋅ ⋅cosψ ⋅⎥ ⎦Dove M è la massa totale della terra e A, B, C I momenti di inerzia rispetto agliassi X, Y, Z, deducibili con ottima approssimazione dalla meccanica celeste.Slide 15Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoG ⋅M⎡ 1 ⎛ A + B ⎞3 B − AV'( σ,ψ,λ)= ⋅⎢1+⋅⎜C− ⎟ ⋅cos2λ22σ ⎣ 2 ⋅σ⋅M⎝ 2 ⎠4 ⋅σM22 ⎤( 1−3 ⋅sinψ) + ⋅ ⋅cosψ ⋅⎥ ⎦Poichè, una grande quantità di osservazioni dimostrano che la terra ha unaforma molto prossima a quella di un solido di rotazione:A= Br2=X2+Y2=σ2⋅cos2ψU=G ⋅M⎡⋅ 1+σ ⎢⎣12 ⋅σ2C − A⋅M⋅⎤⎥⎦1222 2 2( 1−3 ⋅ sin ψ) + ⋅ω⋅σ⋅cosψ = costEQUAZIONE DELLO SFEROIDENon compare λ nell’equazione → Superficie di rotazioneSlide 16Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoLe costanti G, M e C – A, che definiscono lo sferoide, sono di naturameccanica e vanno sostituite con parametri geometrici:- Il semiasse equatoriale → a- Il semiasse polare → cSi ottiene così, con alcune trasformazioni, l’equazione dello sferoide incoordinate polari:σ=a ⋅2( 1- α ⋅ sin ψ)αa − c c= = 1−→ schiacciamentoa aL’equazione nel sistema geocentrico è:2 2 2( X Y + Z )⎛= a ⋅⎜1-α ⋅⎝12+2Z2⎞( ) ⎟ 2 2X + Y + Z ⎠Slide 17Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoConsideriamo ora un ellissoide di rotazione avente gli stessi semiassi a e cdello sferoide. Esso sarà definito nel sistema geocentrico2X + Y2a2+Zc22= 1Dalla definizione di schiacciamento:c=a ⋅2 22 22( 1- α) → c = a ⋅( 1−α) = a ⋅( 1+α − 2α)Lo schiacciamento α vale circa 1/300 e quindi, trascurando il termine α 2 , pari acirca 1/90.000 ≈ 1·10 -5 , si commetterà un errore nella determinazione delsemiasse minore c di circa 35m (errore del tutto accettabile)Quindi, a meno di termini in α 2 :c2= a2⋅( 1−2α)Slide 18Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoL’equazione dell’ellissoide diviene:Sviluppando in serie binomiale il coefficiente della Z 2 e trascurando, al solito, itermini in α 2 e potenze superiori, si ottiene:Ricordando che:−12( 1−2α) a2 2 2X + Y + Z ⋅ =−1( 1−2α) ≈ ( 1+2α)X2+YL’equazione dell’ellissoide, nel riferimento polare, diviene:σ22+ Z2= σOsservando che i termini a e σ sono dello stesso ordine di grandezza, si puòaccettare la sostituzione:2⎛ Z⋅⎜1−2α ⋅⎝ a22= a22 2Z 2a2Z≅σ2=sin⎞⎟⎠ψSlide 19Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoL’equazione dell’ellissoide diviene:σ=a ⋅12( 1- 2α ⋅sinψ) 2Utilizzando ancora lo sviluppo binomiale per il secondo membro e continuandoa trascurare i termini in α 2 , si ottiene:σ=a ⋅2( 1- α ⋅ sin ψ)Che coincide con l’equazione dello sferoide in coordinate polari.L’ELLISSOIDE DI ROTAZIONE COINCIDE CON LOSFEROIDE DI UGUALI SEMIASSI A MENO DI TERMINI IN α 2Slide 20Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Ellissoidi di riferimentoLa geometria ellissoidica, seppur complessa, è più semplice della geometriasferoidica.Il compito dei geodeti è quello di determinare i semiassi maggiore e minore a ec, ovvero a e α. I metodi si basano su misure geometriche (misure di archi dimeridiano e parallelo), su misure di gravità e di tracciamento di orbite di satellitiartificiali.Nel corso degli anni molti geodeti hanno lavorato su tale problema e hannodeterminato valori diversi di a e α:a [m]αBESSEL (1841) 6.377.397 1/299.2CLARKE (1880) 6.378.243 1/293.5HAYFORD (1909) 6.378.388 1/297.0WGS84 (1984) 6.378.137 1/298.257223563Slide 21Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Ellissoidi di riferimentoNOMEannoSemiasse maggiorea (m)Semiasseminore b (m)schiacciamento αUtenti-NoteBounguer 1738 6. 397. 300 1/216.8Delambre 1810 6. 375. 653 1/334.0Everest 1830 6. 377. 276 6. 356. 075 1/300.8 IndiaBessel 1841 6. 377. 397 6. 356. 079 1/299.1 Germania, Indonesia, Paesi BassiAiry 1858 6. 377 . 563 6. 356. 257 1/299.3 Gran BretagnaPratt 1863 6 .378. 245 1/295.3Clarke 1866 6 .378. 206 6. 356. 584 1/294.9 USAClarke modificato 1880 6 .378. 249 6. 356.515 1/293.5 Sud AfricaHayford (Internaz. ) 1909 6. 378. 388 6. 356. 912 1/297.0Usato dalla cartografia italiana.adottata internazionalmente nel 1924Krassovsky 1948 6. 378. 245 6. 356.863 1/298.3 Russia, Paesi OrientaliWGS 60 1960 6. 378. 165 1/298.3calcolato da dati di geodesia spaziale(orbite dei satelliti)National Australian 1965 6. 378. 165 1/298.3WGS 66 1966 6. 378. 145 1/298.25calcolato da dati di geodesia spaziale(orbite dei satelliti)I.U.G.G. 1967 6. 378. 160 6. 356. 775 1/298.25 adottato internazionalmenteSouth America 1969 6. 378. 160 6. 356. 774 1/298.3WGS 72 1972 6. 378. 135 6. 356. 750 1/298.258WGS 84 (GRS) 1984 6. 378. 137 6. 356. 752 1/298.257calcolato da dati di geodesia spaziale(orbite dei satelliti)calcolato da dati di geodesia spaziale(orbite dei satelliti), usato per ladeterminazione del GPSSlide 22Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Il meridiano terrestre come metro di paragoneLa misura della Terra è stata parametro fondamentale anche per la definizione digrandezze che apparentemente non hanno nessun legame con essa.Vi siete mai chiesti, ad esempio, perché un metro è lungo proprio un metro? Ebbenequesta misura deriva dalla lunghezza del meridiano terrestre.La sua storia comincia nel 1792, in Francia, nel periodo della Rivoluzione.Fino ad allora, in Francia come nel resto del mondo, esistevano un’infinità di unità dimisura, diverse non solo da uno Stato all’altro, ma anche all’interno di una regione, diuna provincia o di un distretto. Unità diverse nel nome e a volte diverse nel valore,anche se con lo stesso nome. E per una stessa grandezza, ad esempio la lunghezza,unità diverse, a seconda che si misurassero campi o stoffe o edifici.Questa organizzazione era un’eredità del sistema feudale, che limitava gli scambicommerciali fra le varie aree geografiche, facilitava i raggiri nelle compravendite erendeva difficile una tassazione uniforme.Slide 23Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Il meridiano terrestre come metro di paragoneLo spirito illuminista che guidava la Rivoluzione francese non poteva tollerare questafonte di disuguaglianza fra i cittadini.Questo convinse il governo rivoluzionario ad incaricare la comunità degli scienziati,attraverso l’Accademia delle Scienze, della definizione di un sistema di unità dimisura universale, ricavato da parametri non soggetti all’arbitrio umano.Per soddisfare questo requisito, sembrò ovvio rivolgersi alle grandezze della natura,considerate oggettive e immutabili.Dopo ampie discussioni, per la lunghezza fu deciso che l’unità base sarebbe statapari alla decimilionesima parte dell’arco di meridiano compreso fra il Polo Nord el’Equatore e passante per Parigi.Slide 24Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Definizione della superficie di riferimentoGli studi e le ricerche che sono stati condotti storicamente per la determinazionedella superficie fisica della Terra, e quindi per la determinazione della superficiedi riferimento da utilizzare nelle operazioni di misura, hanno portato adindividuare due differenti superfici:•la prima è una superficie, denominata geoide, che rappresenta la superficieequipotenziale del campo gravitazionale terrestre passante per il livello mediodei mari. Soddisfa la condizione di essere facilmente individuabile fisicamente (ladirezione e il verso del campo gravitazionale possono infatti essere individuaticon facilità), ma non è matematicamente trattabile;•la seconda è un ellissoide di rotazione, cioè un ellissoide biassiale, di forma edimensioni assegnate. E’ una superficie geometrica facilmente trattabile dalpunto di vista matematico, ma non possiede alcun significato fisico.L'utilizzo di queste due differenti superfici di riferimento ha comportato nelposizionamento classico la separazione della determinazione della componentealtimetrica da quella planimetrica.Slide 25Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Slide 26Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di PisaDefinizione della superficie di riferimento• il geoide rappresenta la superficie di riferimento utilizzata per la determinazionedelle quote,• l'ellissoide è utilizzato per la definizione delle coordinate planimetriche.GEOIDE per l’altimetriaELLISSOIDE per la planimetria

QUOTA ELLISSOIDICA E ORTOMETRICA-DEVIAZIONE DELLA VERTICALECome conseguenza, in un punto P della superficie terrestre si potranno definire duenormali, ognuna relativa alla corrispondente superficie di riferimento:la normale al geoide (o verticale)la normale all'ellissoide.Questo comporta che la verticalein un generico punto P del geoidenon coincide con la normaleall’ellissoide.L’angolo da esse formato vienedetto deviazione della verticaleed è dell’ordine di qualchesecondo sessagesimale.Slide 27Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

QUOTA ELLISSOIDICA E ORTOMETRICA-DEVIAZIONE DELLA VERTICALELa relazione tra quota ellissoidica h e quota ortometrica H si esprime definendol'ondulazione del N del geoide:N = h -HP oP'' = NPP o= Hεondulazione del geoide (differenza tra ellissoide e geoide in unpunto).In Italia varia da +37 m in Calabria a +52 m in Val D'Aosta PP' = hquota ellissoidica del punto Pquota ortometrica o quota del punto Pdeviazione della verticale (vale poche decine di secondisessagesimali, e varia da zona a zona).Slide 28Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

QUOTA ELLISSOIDICA E ORTOMETRICA-DEVIAZIONE DELLA VERTICALEN=h-HSlide 29Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

QUOTA ELLISSOIDICA E ORTOMETRICA-DEVIAZIONE DELLA VERTICALELa deviazione della verticale comporta numerose implicazioni, alcune delle qualianche di carattere pratico:è infatti evidente che l'unica direzione fisicamente determinabile è quella dellaverticale, cioè della normale al geoide, ed essa costituisce quindi il riferimentonaturale e fondamentale al quale sono legate le misure di carattere topograficoeseguite sulla superficie fisica della Terra.Gli elementi misurati vengono poi utilizzati per individuare la posizione relativa edassoluta dei punti mediante procedimenti di calcolo da svilupparsi sulla superficie diriferimento e quindi, in generale, sull'ellissoide di rotazione:è quindi evidente che è necessario, almeno in linea teorica, apportare agli elementimisurati, riferiti alla verticale, delle opportune correzioni per dedurne quellicorrispondenti riferiti alla normale ellissoidica.Tali correzioni, sono in generale, molto piccole e di conseguenza possono esseretrascurate nella quasi generalità dei casi, se non per misure di altissima precisione oin condizioni particolari di forti deviazioni della verticale.Slide 30Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Parametri ellissoideConsiderando un ellissoide di rotazione di parametri a e c noti, restanodefinite le quantità:schiacciamentoα2a − c2 a − c= prima eccentricità e =2aa2seconda eccentricitàe'2=a2− c2c2Fra tali quantità sussistono le seguenti relazioni:e'2=2e1−e2e2=2e'1+e'2222( 1−e ) ⋅( 1+e' ) = 1 α = 1−1−ee2= 2α − α2ac=1+e'2ca=1- e2= 1- αSlide 31Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geografiche ellissoidicheLa generatrice, e di conseguenza ogni meridiano, è un ellisse di semiassia e c detta ELLISSE MERIDIANAPreso un punto generico M appartenente all’ellissoide, la normale N adesso relativa incontra l’asse polare di rotazione in C, che rappresenta ilcentro di curvatura dell’ellisse meridiana in M.Latitudine φ→ angolo acuto che N forma con il piano equatoriale XYLongitudine λ → angolo diedro che il semipiano meridiano per M formacon un semipiano meridiano origineSlide 32Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Paralleli → linee di uguale latitudineMeridiani → linee di uguale longitudineCoordinate geografiche ellissoidicheI parametri φ, λ, ogni coppia dei quali individua univocamente il punto M ela direzione N, costituiscono un sistema di coordinate curvilineesuperficiali dette:COORDINATE GEOGRAFICHE ELLISSOIDICHEConsiderando la sezione meridianacontenente M:Latitudine ridotta u → angolocompreso tra il segmento OK e l’asse rLatitudine geocentrica ψ → angolocompreso tra il segmento OM e l’asse rψ < u < φSlide 33Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

tgϕ=Slide 34Equazioni parametriche ellissoideData l’equazione dell’ellissoide di rotazione nel sistema cartesianogeocentrico:2 2 2X + Y Z+ = 122a cscelti i parametri φ, λ ci proponiamo di scrivere le equazioni parametrichedell’ellissoide. In un piano meridiano Zr l’equazione dell’ellisse meridianarisulta:2 2r Z+ = 12 2a cI coseni direttori della normale ad una curva di equazionef(r,Z)=0, sono proporzionali alle derivate parziali di questafunzione lungo le due direzioni di riferimento:∂fcosϕ= k ⋅∂rZra⋅c222r= k ⋅2a⇒⎛ π ⎞∂f2Zcos⎜−ϕ⎟ = sinϕ= k ⋅ = k ⋅2⎝ 2 ⎠∂Zc2c2Z = r ⋅ tgϕ⋅ = r ⋅ tgϕ⋅( 1−e )2aSostituendo Z nell’equazione dell’ellisse meridianaTopografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

aEquazioni parametriche ellissoide2( 1−e )22r 2 22Ricordando che:Si ha:r22 22r ⋅ tg ϕ ⋅2 a 2 2+ = 1 ⇒ r + ⋅r⋅ tg ϕ ⋅22cc22[ 1+tg ϕ ⋅ ( 1−e )]=aca2221=1−e22( 1−e )= ar2=1+a2tg ϕ ⋅22( 1−e )=2 2a ⋅cosϕ22 2cos ϕ + sin ϕ − e=2⋅ sin ϕ2 2a ⋅cosϕ2 21−e ⋅ sin ϕr=a ⋅cosϕ1−e2⋅ sin2ϕPrima equazione parametricadell’ellisse meridianaSlide 35Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Z = r ⋅ tgEquazioni parametriche ellissoideSostituendo r si ottiene la seconda equazione parametrica:a ⋅ cosϕϕa ⋅sinϕ⋅2( 1−)ϕ 2 2e⋅( 1−e ) =⋅tgϕ⋅( 1−e ) =2 22 21−e⋅sin1−e⋅sinPoichè nel sistema geocentrico ogni ellisse meridiana può essereindividuata dalla longitudine λ e risulta che:ϕX=r ⋅cosλY=r ⋅ sinλLe equazioni parametriche dell’ellissoide sono:⎧ a ⋅cosϕ⋅cosλ⎪X =W⎪a ⋅cosϕ⋅ sinλ⎨Y=⎪ W2⎪ a ⋅( 1−e ) ⋅ sinϕ⎪Z=⎩ WdoveW=1- e22⋅ sin ϕSlide 36Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoidePer un punto posto ad altezza ellissoidica h, le equazioni diventano:⎧⎪X =⎪⎪⎨Y=⎪⎪⎪Z=⎩⎛⎜⎝⎛⎜⎝⎛⎜⎝aWaWaW⎞+ h⎟ ⋅cosϕ⋅cosλ⎠⎞+ h⎟ ⋅cosϕ⋅ sinλ⎠⋅2( 1−e )⎞+ h⎟ ⋅ sinϕ⎠aWcosϕ=raW= NParametro che vedremo essere ilraggio di curvatura di unaparticolare sezione dell’ellissoideSlide 37Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideESEMPIEs. 1Parametri dell’ellissoide Internazionale:a=6’378’388 me 2 = 0.00672267punto A: ϕ = 43° 42’ 45.418’’ λ = 1° 16’ 51.012’’punto B: ϕ = 43° 41’ 05.212’’ λ = 1° 18’ 36.310’’punto C: ϕ = 43° 43’ 08.544’’ λ = 1° 19’ 49.836’’ES. 2ϕ = 45°λ = 30°h = 350 ma = 6’378’388 me 2 = 0.00672267Slide 38Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideESEMPIO 1:Parametri dell’ellissoide Internazionale:a=6’378’388 me 2 = 0.00672267punto A: ϕ = 43° 42’ 45.418’’ λ = 1° 16’ 51.012’’SoluzioneSlide 39Punto Aϕ =λ =42⋅60+ 45.41843 ° 42' 45.418''= 43° += 43°, 71261611360016⋅60+ 51.0121 ° 16' 51.012''= 1° += 1°. 2808366673600Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideX =Y =Z =a cosϕcosλ= 4'616'659.048m2 2( 1−e sin ϕ )a cosϕsinλ= 103'221.763m2 2( 1−e sin ϕ )a( 1−e2( 1−e2)sinϕ2sin ϕ )= 4'385144 ' . 185mSlide 40Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideESEMPIO 2:ϕ = 45°λ = 30°h = 350 ma = 6’378’388 me 2 = 0.00672267aX = (+ h)cosϕcosλ=2 2( 1−esin ϕ )= 3912744523 ' ' . maY = (+ h)cosϕsinλ=2 2( 1−esin ϕ )= 2'259024104 ' . m2a( 1−e)Z = (+ h)sinϕ=2 2( 1−esin ϕ )= 4'487676524 ' . mSlide 41Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideESEMPIO 3:Determinare le coordinate cartesiane geocentriche del puntoIGM95 105703 – Cascina di coordinate geografiche WGS84:lat 43° 40’ 29.524’’ lon 10° 34’ 01.239’’ q ell62.04ma WGS84= 6378137 α WGS84= 1/298.257223563ϕ = # ° +λ = # ° +e2#'/60#'/602= 2α-α++#''/3600=43.67486778 °#''/3600=10.56701083 °= 0.006694379992N =aWW== 6388342.281m1−e22sin ϕ = 0.998402515⎧X=⎪⎨Y=⎪⎩Z=( N+h)( N+h)⋅cosϕ⋅cosλ= 4542182.681m⋅cosϕ⋅sinλ= 847339.830m2( N⋅( 1- e ) + h)⋅sinϕ= 4382077.144mSlide 42Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideIl passaggio inverso, da coordinate cartesiane geocentriche ageografiche, è più complesso.Non sono esplicitabili direttamente le relazioni di φ e di h.CALCOLO IN FORMA ITERATIVAIl valore di λ è deducibile dalle equazioni parametriche in X e Y:Yλ = arctgXDalle stesse equazioni, il raggio del parallelo risulta:r=X2+Y2=( N + h) ⋅cosϕSlide 43Dividendo l’equazione parametrica in Z per r:Zr=2[ N⋅( 1−e ) + h]( N + h)⋅ senϕ=⋅cosϕ( N + h)− eN + h22⋅N⎛ e ⋅N⎞⋅ tgϕ= ⎜1−⎝ N + htgϕTopografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa⎟ ⋅⎠

Equazioni parametriche ellissoideTrascurando in prima approssimazione il valore piccolo:⎛⎜1−⎝2e ⋅N⎞⎟N + h ⎠si ottieneϕ =Zarctgrdi primaapprossima zioneN=1−ea22⋅ sen ϕh=Xcosϕ⋅cosλ− Nϕ =Zarctg2⎛ e ⋅N⎞r ⋅⎜1-⎟⎝ N + h ⎠Il calcolo iterativo di N, h e φ continua fino a quando, posto un intervallo diconvergenza ε, accade che:ϕ −ϕnn−1

Equazioni parametriche ellissoideSOLUZIONI IN FORMA CHIUSASi riporta qui una soluzione dovuta a Bowring che ha il vantaggiodi essere in forma chiusa:Yλ = arctgX2Z + e b sinr − e acos' 3ϕ = arctg2 3h=r−cosϕNθθSlide 45Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoidedove r è la distanza dall'assepolare, ricavabile da:r = X2+Y2e’ è la "seconda eccentricità":e'=2e1−e2e θ è un angolo ausiliariofornito da:θ=⎛arctg⎜⎝Zarb⎞⎟⎠Slide 46Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideEsempio 1:Le coordinane geocentriche di un punto nel sistema WGS84 sono leseguenti:X = 4523182.126 mb=6356752.31a=6378137mY = 896756.782 m e 2 =0.00669438Ellissoide WGS84Z = 4391884.321 m e’ 2 =0.00673950tgλ= 896756.782 =0.198257943λ= 11°.21392680 = 11°12’50.1365’’r=(4523182.126 2 +896756.782 2 ) 1/2 =4611219.933 mSlide 47Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Equazioni parametriche ellissoideza =rb0.955638439Slide 48Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliConsideriamo un punto P giacente sull’ellissoide e la sua normale:SEZIONE NORMALESEZIONE OBLIQUALinea di intersezione con l’ellissoide dei piani→ appartenenti al fascio di piani aventi comesostegno la normale in P.→ Tutte le altre intersezioni tra un piano che noncontiene la normale e l’ellissoide.Slide 49Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliLe sezioni normali in P hanno raggio di curvatura variabile a secondadell’angolo che formano con il piano che definisce la sezione normaleMERIDIANO.SEZIONI NORMALI PRINCIPALI- Meridiano per P- Ortogonale al meridiano per P → piano che contiene la tangente alparallelo per PRaggi di curvaturaprincipaliρ → raggio minimoN → raggio massimoSlide 50Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliDeterminiamo le espressioni dei raggi principali di curvatura:L’equazione ricavata in precedenzaper le ellissi meridiane è:ra22Z+c22= 1In una curva piana il raggio dicurvatura è il limite del rapporto tra unelemento di arco ds e l’angolocompreso fra le normali alla superficiecondotte agli estremi del segmento ds(→ differenza di latitudine).ds dr2+ dZρ = =dϕ dϕ2Slide 51Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliDeriviamo le equazioni parametriche dell’ellissoide trovate in precedenza:r2a ⋅cosϕa ⋅ sinϕ⋅( 1−e )= Z =2 2W = 1- e2 ⋅ sin 2ϕ2 21−e ⋅ sin ϕ1−e ⋅ sin ϕdr=dϕ- a ⋅ sinϕ⋅ W + a ⋅cosϕ⋅W12W222a ⋅ sinϕ⋅ W − a ⋅cosϕ ⋅ sinϕ⋅ e= −3W3 222a ⋅ sinϕ− a ⋅ sin ϕ ⋅ e − a ⋅cosϕ ⋅ sinϕ⋅ e= −3W2 22a ⋅ sinϕ− a ⋅ sinϕ⋅ e ⋅( sin ϕ + ⋅cosϕ )= −3Wa ⋅= −analogamente =3Wdϕ2⋅ 2e22( 1−e ) ⋅ sinϕdZ a ⋅ ( 1−e )2⋅ sinϕ⋅cosϕW3⋅cosϕSlide 52Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliSi ottiene quindi:ρ=2⎛ dr ⎞⎜ ⎟⎝ dϕ⎠⎛ dZ ⎞+ ⎜ ⎟⎝ dϕ⎠2=a2⋅2 2 2 22 2 22( 1−e ) ⋅ sin ϕ + a ⋅( 1−e ) ⋅cosϕ a ⋅ ( 1−e )W6=W3ρ=a ⋅2( 1−e )W3Teorema di Meusnier:Il raggio di curvatura in un punto P disezione obliqua (r) è uguale al raggio dicurvatura della sezione normale (N),corrispondente al piano che contiene latangente in P alla sezione obliqua,moltiplicato per il coseno dell’angoloformato dai piani delle due sezioniSlide 53Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliPer il teorema di Meusnier, pensando al parallelo per P come unasezione obliqua, che avrà raggio di curvatura r:r = N⋅cosϕrN = =cosϕa ⋅cosϕ1⋅ =W cosϕaWN =aWDalle espressioni di ρ e di N otteniamo:N - ρN=⎛⎜⎝aWa ⋅−2( 1−e )W3⎞⎟ ⋅⎠Wa=2 2e ⋅cosϕ2 21- e ⋅ sin ϕ- N è sempre maggiore o uguale a ρ- La differenza è massima all’equatore ( φ = 0° )- La differenza è minima ai poli ( φ = 90° )- La differenza fra i due raggi di curvatura è dell’ordine di e 2 ≈ 1/150Slide 54Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geograficheSlide 55Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geograficheSlide 56Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geograficheSlide 57Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geograficheSlide 58Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geograficheSlide 59Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geograficheSlide 60Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Coordinate geograficheSlide 61Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliSlide 62Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliSlide 63Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Raggi di curvatura e sezioni normaliIl raggio di curvatura R αdi una sezione normale generica, che forma unangolo α, chiamato AZIMUT, con il meridiano, in funzione del raggio dicurvatura minimo ρ e massimo N è dato da:1Rαcos=ρ2α+2sin αNTeorema di EULEROSlide 64Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloLUNGHEZZA DI ARCHI FINITI DI PARALLELO E DIMERIDIANOLa determinazione della lunghezza di archi finiti di parallelo edi meridiano ha notevole importanza soprattutto in relazionealla determinazione geometrica dei parametri dell’ellissoideterrestre.Triangolo infinitesimo sull'ellissoidedi rotazioneSlide 65Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloLa lunghezza di un arco di parallelo di latitudine ϕ, compreso frale longitudini λ 1e λ 2, si ottiene integrando:λ2l pDove:rd= ∫ λ = r ⋅λ1( λ −λ)21r raggio del parallelor=acosϕ2 21−e sin ϕle longitudini λ 1 e λ 2vanno espresse in radianti.Slide 66Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloAnalogamente per il calcolo della lunghezza dell’arco dimeridiano, integrando tra due valori della latitudine ϕ 1e ϕ 2:ϕ(2) (2 21 e 1 e sin ϕ) dϕ222l m= ∫ ρdϕ= a − ∫ −ϕ1ϕϕ13−Dove:ρ raggio del meridianoρ =2a( 1−e )32 2( 1−e sin ϕ) 2Slide 67Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloL’integrale si può risolvere solo tramite uno sviluppo in serie(Andrae) e si ottiene:= a⋅(2) ( )1−el m2= ∫ ρ ⋅⋅[A ϕ −ϕ2ϕϕ11dϕ≅− B(sin2ϕ−sin2ϕ) +21+C(sin4ϕ−sin4ϕ)21−D(sin6ϕ−sin6ϕ)21++E(sin8ϕ−sin8ϕ)21−F(sin10ϕ−sin10ϕ)21+ ......]N.B. le latitudini ϕ 1 e ϕ 2vanno espresse in radianti.Slide 68Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

A = 1+BCD===121416⎛⎜⎝⎛⎜⎝⎛⎜⎝3e43e415e6435e51245+ e6415+ e16105+ e256+1 ⎛ 315E = ⎜ e8 ⎝16384F+1 ⎛ 693= ⎜ e10⎝1310722246844175+ e256525+ e512+315e204810Archi di meridiano e parallelo683465e65536⎞+ ...... ⎟⎠662205e409611025+ e163842205 8+ e204831185+ e131072108⎞+ ...... ⎟⎠10395+ e163841043659+ e6553672765+ e65536810⎞+ ...... ⎟⎠1010⎞+ ...... ⎟⎠+ ......⎞+ ...... ⎟⎠Slide 69Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloIl primo termine dello sviluppo dell’integrale è decisamenteimportante e dipende dalla differenza delle latitudini; questevengono misurate con metodi astronomici e quindi riferite allaverticale, mentre lo sviluppo in serie si riferisce alla normale.Le latitudini misurate quindi risentono della cosiddetta deviazionedella verticale.Se l’arco di meridiano è misurato direttamente, per esempio con losviluppo di una base geodetica così come si è fatto dal seicento inpoi, le incognite diventano a ed e 2 :è proprio questa la via percorsa nel secolo XVIII e XIX per calcolarei parametri a e b.Fu proprio allora che ci si accorse dell’influenza del primo termine,cioè del valore delle latitudini astronomiche anziché ellissoidiche sulcalcolo delle incognite.Slide 70Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloSi cercò di ovviare misurando archi di meridiano qua e là per la terra, alatitudini diverse (spedizioni in Perù, 1735-1737 e poi in Lapponia, 1736-1737 e altre ancora) cercando quindi di rendere accidentale l’errore dovutoalla misura di ϕ e perciò significativo il valore medio dei parametri cosìdeterminati.Poiché nella misura diretta (per via astronomica) delle coordinategeografiche è possibile raggiungere precisioni dell'ordine di 0'',2l'approssimazione del posizionamento planimetrico è dell'ordine di circa6m, infatti:⎛ 0.2 π ⎞⎜ ⎟ 6370 ≅ 0.006 km ≅ 6 m⎝ 3600 180 ⎠Questa precisione è inadeguata ai fini topografici e non omogenea conquella raggiungibile nella misura delle distanze con i distanziometrielettronici, che è dell’ordine di 10 -6 ⋅D, pari a circa 5≅6 cm per le massimedistanze operative di 50≅60km.Da ciò deriva la necessità di definire la posizione planimetrica dei puntiattraverso misure di angoli e di distanze procedendo in un secondo tempoal calcolo delle coordinate geografiche dei punti; queste dovranno esserericavate con approssimazione di 1/1000 di secondo per ottenere lacongruenza con la corrispondente precisione della distanza.Slide 71Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloESEMPIO 5:Calcolo di un arco di paralleloSi vuole determinare sull’ellissoide Internazionale un arco diparallelo pari a 1” alla latitudine ϕ 1 =45°33’00’’.I parametri dell’ellissoide Internazionale sono:a=6’378’388 me 2 =0.00672267lp( λ − λ )2λ2= ∫rdλ= r ⋅λ113600o1:= 1" =xr= 90( λ − λ )2r0.000004848oπ:21Slide 72Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Wlacosϕ2 2[ 1−e sin ϕ]2 2[ 1−e sin ϕ]1= 1.001717346WaN = = 6'389'341.899 mWr = 4'474'370.316 mP=ϕ ===o45 33'00''21.692Archi di meridiano e parallelom=45o=+aW3360cosϕ=o45 ,55= 0.998285598Slide 73Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloESEMPIO 6:Calcolo di un arco di meridianoSi vuole determinare sull’ellissoide Internazionale un arco dimeridiano pari a 1” compreso tra le latitudini:ϕ 1 =45°33’00’’ϕ 2 =45°33’01’’I parametri dell’ellissoide Internazionale sono:a=6’378’388 me 2 =0.00672267ϕ( 1−e2) ( 1−e2sin2ϕ) dϕ222l ρdϕam=∫ϕ1=ϕ∫ϕ13−Slide 74Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Archi di meridiano e paralleloϕ(2) (2 21−e 1−e sin ϕ) dϕ≅222l m= ∫ ρdϕ= a ∫ϕ1ϕϕ13−≅a⋅( 1−e2) ⋅ A( ϕ −ϕ)2132454175611025843659A = 1+e + e + e + e + e4 64 256 16384 65536( ϕ )r− ϕ = 1" =2 10.00000484810+ ...... = 1.00507398883l = 30. 870 mmSlide 75Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Esempi di coordinate geograficheEsempiλ Torino= 7°.42 Eλ Trieste= 13°.46 Eλ Milano= 9°.12 Eλ Bologna= 11°.20 Eλ Firenze= 11°.16 Eλ Genova= 8°.55 Eλ Pisa= 10°.24 Eλ Roma= 12°.41 Eλ Napoli= 14°.15 Eλ Reggio Calabria= 15°.39 Eλ Palermo= 13°.22 Eλ Cagliari= 9°.6 Eϕ Torino= 45°,4 Nϕ Trieste= 45°,39 Nϕ Milano= 45°,28 Nϕ Bologna= 43°,30 Nϕ Firenze= 44°,46 Nϕ Genova= 44°,25 Nϕ Pisa= 43°.43 Nϕ Roma= 41°.48 Nϕ Napoli= 40°.21 Nϕ Reggio Calabria= 38°.6 Nϕ Palermo= 37°.7 Nϕ Cagliari= 39°.13 NSlide 76Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideDefinizione di distanze e angoli sulla superficie ellissoidica diriferimento•Poiché tra due punti di una superficie curva possono essere tracciate lineedi natura geometrica diversa occorre definire quale tra queste ha laproprietà di rappresentare la distanza misurabile fra due punti;• se due di tali linee escono da un punto O si definirà come angolo fraqueste l'angolo che le tangenti alle linee nel punto O formano fra loro.Definizione di distanzaSi può dimostrare che sulla superficie di riferimento, la linea checongiunge due punti, non troppo distanti tra loro, e che possiede leproprietà di una distanza (è unica e rappresenta il percorso di minimalunghezza) è la geodetica.Slide 77Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideLe geodetiche godono della seguente proprietà:la linea geodetica è quella particolare linea della superficie che gode dellaproprietà di avere la normale principale in ogni suo punto coincidente conla normale alla superficie in quel punto.•Le geodetiche dell'ellissoide sono linee gobbe, non sono cioè contenute inun piano e il loro raggio di curvatura in un punto viene valutato mediante ilTeorema di Eulero:221 cos α senα= +R gρ N•Le geodetiche della superficie sferica, sono archi di circonferenzamassima.In questo caso i punti vengono congiunti da archi di circonferenzamassima e le misure da fare per individuarne la posizione relativa sono lelunghezze di archi di circonferenza massima e angoli fra circonferenzemassime;•Le geodetiche del piano, sono rette (qualsiasi altra curva del piano ha lanormale principale giacente sul piano stesso), ed in questo caso simisurano lunghezze di segmenti di retta ed angoli fra rette.Slide 78Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideIl fatto che le geodetiche sull’ellissoide siano linee gobbe non è unadifficoltà dal punto di vista della costituzione di una trigonometriaellissoidica, perfettamente definibile a parte la complicazione delleformule (è facile risolvere un triangolo piano ed anche un triangolosferico, ma la risoluzione di un triangolo sull'ellissoide i cui lati sianogeodetiche ellissoidiche comporta l'uso di formule molto complesse).E’ una complessità dal punto di vista delle misure, in quanto è intuibileche può essere facile, ad esempio, misurare la lunghezza di una lineacontenuta in un piano ma non altrettanto facile misurare la lunghezzadi una linea gobba, non fosse altro per i problemi che sorgerebbero perindividuarla.Slide 79Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideLe sezioni normali sono geodetiche? DipendeCOMPORTAMENTO DELLE SEZIONI NORMALISoffermiamoci sul comportamento delle sezioni normali sull’ellissoide inrelazione alle analoghe sezioni tracciate sulla sfera e sul piano.SferaSu di una sfera si prendano in considerazione due diversi punti A e B ed ilpiano normale in A passante per B:è facile constatare che questo piano normale interseca la sfera medesimasecondo un arco di cerchio massimo coincidente con quello intersecato dalpiano normale in B che passa per A.Infatti, le due normali condotte alla sfera nei punti A e B, entrambeincidenti nel centro C della stessa sfera, risultano fra loro complanari el'arco di cerchio massimo intersecato sulla sfera dal piano che le contienedefinisce una ed una sola sezione normale.SULLA SFERA LE SEZIONI NORMALI SONO GEODETICHESlide 80Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoidePianoAnaloga constatazione può essere fatta allorché si prendano inconsiderazione due distinti punti A e B disposti sopra un piano.Infatti conducendo per il primo punto A il piano normale contenente B,esso intersecherà il piano che li contiene lungo una retta coincidente conl'intersezione determinata, sullo stesso piano dato, dal piano normalecondotto per il secondo punto B e contente il primo punto A.Tale circostanza è evidentemente dovuta al parallelismo delle due normalial piano dato per i punti A e B, che con questo definiscono un'unicasezione normale.SUL PIANO LE SEZIONI NORMALI SONO GEODETICHESlide 81Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideEllissoideInfine, prendendo in considerazione l'ellissoide di rotazione si constatainvece come questa coincidenza venga a mancare, poiché le normalicondotte per differenti punti della superficie, pur intersecando tutte l'assedi rotazione, non risultano sempre incidere in uno stesso punto.Per cui, presi sull'ellissoide dirotazione due distinti punti A e B, siconsideri la sezione normaleprodotta dal piano che contiene lanormale in A ed il punto B, questasezione differisce dalla sezionenormale reciproca prodotta dalpiano che contiene la normale in B eil punto A.IN GENERALE SULL’ELLISSOIDE LESEZIONI NORMALI NON SONOGEODETICHESlide 82Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideAd esempio la duplicità delle sezioni normali non consente di ricorrere atali linee per definire in modo univoco i triangoli ellissoidici:infatti dati tre punti esistono in genere sei sezioni normali che licongiungono a due a due.Sezioni normali reciproche per tre puntiSlide 83Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideFanno eccezione i soli casi in cui i due distinti punti A e B giaccionoo sullo stesso piano meridiano o sul parallelo di riferimento,l’equatore:soltanto in questi due casi le normali per A e per B risultano infatti tra lorocomplanari.Esaminando con maggior attenzione questa circostanza, si può evidenziareche gli scostamenti tra le due sezioni normali reciproche sono funzionicrescenti dell'eccentricità e dell'ellisse meridiana generatrice dell'ellissoidedi rotazione, per cui si può concludere che più ci si allontana dalla formasferica, più sensibile risulta lo sdoppiamento delle sezioni normalireciproche.Da un punto di vista teorico quindi, dati due punti A e B, le sezioninormali sull’ellissoide non sono determinate in maniera univoca enon possono per questo definire la distanza da un punto all’altro.Slide 84Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

EQUAZIONI DELLE GEODETICHEIn generale, data una superficie Φ(x,y,z)=0, i coseni direttori dellanormale alla superficie valgono:1N∂Φ⋅ ;1N∂Φ⋅ ;∂x∂y∂z⎝ ∂x⎠ ⎝ ∂y⎠ ⎝ ∂z⎠Considerando una linea appartenente alla superficie, data in formaparametrica x=x(s), y=y(s), z=z(s), i coseni direttori della normale a talelinea sono:Imponendo la coincidenza delle due normali:Da cui ad esempio:1N∂Φ⋅Angoli e distanze sull’ellissoideconN =222d x d y d zR⋅;R⋅;R⋅222ds ds ds22∂Φd y ∂Φd x⋅ − ⋅22∂xds ∂yds⎛ ∂Φ⎞⎜ ⎟= 02⎛∂Φ⎞+ ⎜ ⎟2⎛ ∂Φ⎞+ ⎜ ⎟∂Φ∂x2d x2ds2∂Φ∂y=2d y2ds∂Φ= ∂z2d z2dsSlide 85Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideNel nostro caso la superficie descritta da Φ è l’ellissoide di rotazione.Riscriviamone l’equazione:2X + Y2a2Z+csapendoche22= 1 →2a -c2aX22+ Y2c= 1−aa+c2222→⋅Z2ac22−a2= 01=1−e2→X2+ Y2⎛−⎜a⎝2a−c22⋅Z2⎞⎟⎠= 0Φ(X,Y,Z) =Risultaquindi:∂Φ∂x= 2xeXSostituendo nell'equazionetrovatainprecedenza:22d y d xx⋅− y⋅22ds ds2+ Y∂Φ∂y= 02⎛−⎜a⎝2= 2y→2Z−1−edds2⎞⎟⎠= 0⎛ dy dx⎜x⋅− y⋅⎞ ⎟ = 0⎝ ds ds⎠→x⋅dyds− y⋅dxds= cost.Slide 86Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Slide 87Si sono viste le equazioni parametriche dell’ellissoide:X = x(s) = r·cosλY = y(s) = r·sinλda cui: dX dλ dr dλ= −r⋅sinλ⋅ + cosλ ⋅ = −Y⋅ds ds ds dsdY dλ dr dλ= r ⋅cosλ⋅ + sinλ ⋅ = X⋅+ sinλ ⋅ds ds ds dsSostituendo nell’equazione:dY dXX⋅− Y⋅ds dsdλX⋅+ X⋅sinλ⋅dsdλds2 2( X + Y ) ⋅ + ( X⋅sinλ− Y⋅cosλ)r2⋅dλds+= costdrds+ Y2⋅Angoli e distanze sull’ellissoidedλds− Y⋅cosλ⋅drdsdrds= costdrds= cost( r ⋅cosλ⋅sinλ−r⋅sinλ⋅cosλ) ⋅ = cost⋅+ cosλ ⋅Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisadrdsdrds

Angoli e distanze sull’ellissoidedλr 2 ⋅ = costdsUn triangolo infinitesimo ABP sull’ellissoide può essere considerato piano.Se α è l’azimut della geodetica PB, si ha:dλ sinαr ⋅dλ= ds⋅sinα→ =r ⋅sinα= costds rTEOREMAdiCLAIRAUTSulle superfici di rotazione è costante, per ogni punto di una geodetica, ilprodotto del raggio del parallelo per il seno dell’azimut della geodetica.Slide 88Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideLa costante è tipica per ogni geodetica e viene chiamata COSTANTE diCLAIRAUT.Le linee geodetiche di una superficie di rotazione sono definibili consemplicità.Se da un punto P esce una geodetica con α = 50gon (NE), l’azimut cresceman mano che la geodetica si allontana dal punto, in quanto il raggio delparallelo diminuisce.Se P ha latitudine φ, il raggio di curvatura della sezione normale diazimut α è espresso dal teorema di Eulero. Il valore R αrappresenta ancheil raggio di curvatura della geodetica, che in P ha un azimut pari ad αSlide 89Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

ESEMPIO 7:Angoli e distanze sull’ellissoideSull’ellissoide di Hayford si consideri la geodetica uscente con azimutα=60° da un punto di latitudine 43°. Calcolare l’azimut della geodetica inP’ di latitudine φ=44° e P’’ con φ=45°.φW1−e2sin 2ϕP 43° 0.9984353459 4672168.001P’ 44° 0.9983766693 4595688.673P’’ 45° 0.9983179178 4517800.72Per il teorema di Clairaut: r · sinα = cost=a⋅cosϕr =W4672168.001 · sin 60° = cost → cost = 4046216.18α = sin−1costr ϕP’ → α = 61.69517°P’’ → α = 63.58771°Slide 90Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Angoli e distanze sull’ellissoideDefinizione di angolo azimutale e azimutAngolo azimutaleConsiderati tre punti A,B,O sulla superficie di riferimento, l'angoloazimutale AOB tra le geodetiche OA e OB è l'angolo formato dalle tangentiin O alle due linee.AzimutConsiderati due punti A e B sulla superficie diriferimento, l'azimut di B rispetto a A è l'angoloche la tangente alla geodetica AB forma con latangente, diretta verso nord, al meridiano in A.Tale angolo viene definito come azimut dellageodetica, è computato a partire dal meridiano insenso orario e può assumere valori compresi tra0 e 2π.Slide 91Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Teoremi geodesia operativaLa geometria sulla superficie di riferimento (ellissoide) si può costruireconsiderando figure geometriche i cui lati siano archi di geodeticheellissoidiche.Si mettono in evidenza le difficoltà di misurare rigorosamente la lunghezzadi un arco di geodetica come pure di misurare l’angolo fra due geodetiche(angolo fra le tangenti alle geodetiche uscenti da un punto).E' opportuno dunque definire le misure che un geodeta o untopografo possono eseguire.Come conseguenza della posizione fatta di assumere come superficie diriferimento l’ellissoide le misure di angoli e distanze andrebbero eseguitecon riferimento alla normale all’ellissoideMa le misure che si possono eseguire sulla superficie fisica fannoriferimento alla verticale, cioè alla normale al geoide, conseguenza delfatto che gli strumenti di misura hanno assi che si possono con facilità eprecisione orientare rispetto alla verticale, ad esempio mediante l'utilizzodi una livella.Slide 92Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Teoremi geodesia operativaGli angoli che si misurano sono quindi sempre riferiti al geoide per cui,stante le differenti direzioni della normale al geoide e della normaleall'ellissoide, equivalgono teoricamente ad angoli tra sezioni oblique suquest'ultimo.Questa incongruenza si può teoricamente e volendo anche praticamentesuperare apportando delle correzioni.Ma è da tenere presente che le incertezze, che inevitabilmenteaccompagnano i risultati delle misure sia angolari sia di distanza,determinano, per conseguenza, incertezze nella posizione ellissoidica deipunti. Queste incertezze potrebbero risultare dello stesso ordine digrandezza delle correzioni che si dovrebbero apportare alle misure perriferirle al geoide.Slide 93Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Teoremi geodesia operativaLa sostanza di quanto sopra costituisce l'essenza dei teoremi dellageodesia operativa:qualunque misura di azimut, angolo o distanza eseguita con i mezziattualmente a disposizione dei geodeti e dei topografi sulla superficiefisica, può ritenersi eseguita con riferimento ad archi di geodetica sullasuperficie di riferimento.• 1° teoremaPer lunghezze fino a circa 200 Km posso confondere angoli tra lineegeodetiche con angoli tra le corrispondenti sezioni normali• 2° teoremaPer lunghezze fino a 200 Km posso confondere la lunghezza dellageodetica con le lunghezze delle corrispondenti sezioni normaliSlide 94Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Teoremi geodesia operativaPertanto tale incongruenza viene accettata e si procede nell’ipotesi che simisurano angoli e distanze con riferimento al geoide, ma i risultati dellemisure si reputano uguali a quelli che si sarebbero ottenuti effettuando lemisure con riferimento all’ellissoide.Inoltre, si misurano lunghezze di archi di sezioni normali e angoli frasezioni normali, tra l'altro non unicamente definite, mentre si dovrebberomisurare lunghezze di archi di geodetica ed angoli fra le tangenti allegeodetiche.Slide 95Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenAl riguardo gli sviluppi di Puiseux-Weingarten forniscono la possibilità divalutare:1. La differenza fra la lunghezza dell'arco di sezione normale e la lunghezzadell'arco di geodetica2. La differenza di azimut fra sezioni normali e geodetiche3. L'approssimazione conseguibile nella determinazione delle coordinate deipunti, allorché vengano nell'ordine presi in considerazione: l'ellissoide dirotazione, la sfera e il piano, al variare della latitudine ϕ o, della lunghezzas e dell’azimut α della geodetica.Slide 96Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Introduciamo un sistema di riferimento euleriano con l’asse Z coincidentecon la normale all’ellissoide in O, l’asse Y coincidente con la tangente almeridiano in O e diretto verso Nord e l’asse X coincidente con la tangenteal parallelo in O e diretto verso Est.Le formule di Puiseux-Weingartenservono allo studio delle proprietà dicurvatura della geodetica e nellasoluzione dei problemi della GEODESIAOPERATIVA.Tali sviluppi esprimono le coordinatenel sistema euleriano di un punto P ell(x,y,z) dell’ellissoide, in funzionedell’arco s di geodetica, compreso tral'origine O della terna euleriana e P, edell’azimut α di tale geodeticanell'origine del riferimento euleriano(coordinate geodetiche polari delpunto P (s,α).Slide 97Sviluppi Puiseux-Weingarten⎧⎪x⎪⎪⎨y⎪⎪⎪z⎪⎩PellPellPell2⎡ s= s ⋅ senα⎢1−⎣ 6ρNo2⎡ s= s ⋅cosα⎢1−⎣ 6ρNo2s= −2Rgoo2 22⎛ e sin α cos ϕ ⎞⎤o⎜1−⎟2 2 ⎥⎝ 1−e sin ϕo⎠⎦⎛ e⎜1−⎝222cos α cos ϕ ⎞⎤o⎟21−e⎥⎠⎦Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-Weingarten1. Differenza tra archi di geodetica e archi di sezione normalePer quanto riguarda la differenza tra archi di geodetica s e archi di sezioninormali s‘, assumendo la lunghezza dell’arco di geodetica s=1000 km sipuò calcolare che la differenza fra la lunghezza dell'arco di sezionenormale e la lunghezza dell'arco di geodetica non supera il centimetro,ovvero l’errore relativo è dell’ordine di 10 -8 .s' −s=s1360⋅s42 2N Rα2⎛ e⋅⎜⎝1−ePoiché i metodi di misura della distanza utilizzati non consentono diraggiungere precisioni superiori a 10 -6 ÷ 10 -7 è perfettamente giustificatoritenere che misure eseguite secondo archi di sezione normale diano glistessi risultati delle misure eseguite secondo archi di geodetica.22⎞⎟⎠24⋅sin2α⋅cosϕSlide 98Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

La differenza di azimut fra sezioni normali (A) e geodetiche (α),considerando il caso in cui tale differenza è massima, e cioè all’equatore e aparità di lunghezza dell’arco s di geodetica (circa 300 km), è dell’ordine delcentesimo di secondo sessagesimale (0.03’’).A −α=Sviluppi Puiseux-Weingarten2. Differenza tra i due azimuts2⋅e2⋅sin2α⋅cos212⋅N⋅R1−eαTale differenza è nulla ai poli (dove geodetiche, sezioni normali e meridiani -che sono geodetiche- coincidono).Se si tiene conto che la precisione di misura degli angoli raggiunge almassimo qualche decimo di secondo sessagesimale (0,1"÷0,2"),π 10.1''⋅ ⋅3600 180ossia in radianti a 5x10 -7 ,e che non è possibile, per effetto della curvatura terrestre, effettuaremisure fra punti distanti più di 200 km, si può concludere che una misura diazimut, anche se effettuata con riferimento a una sezione normale puòsempre considerarsi riferita a una geodetica.2ϕSlide 99Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenQuindi tutto ciò porta a concludere che una misura di azimut riferita aduna sezione normale dell’ellissoide può di fatto considerarsi uguale aquella relativa alla geodetica corrispondente.In altre parole: gli angoli tra due sezioni normali e tra due geodetichepossono considerarsi uguali nei limiti di precisione degli attuali strumentidi misura .Differenza tra i due angoli azimutaliAnaloga conclusione si può trarre per la misura degli angoli azimutalidato che per un angolo azimutale, considerato come differenza tra dueazimut, si potrebbero avere al massimo discrepanze doppie rispetto aquelle appena messe in evidenza.Slide 100Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

3. Approssimazione conseguibile nella determinazione dellecoordinate dei punti, allorché vengano nell'ordine presi inconsiderazione: l'ellissoide di rotazione, la sfera e il pianoSUPERFICIE SFERICAScriviamo gli sviluppi di Puiseux-Weingarten per una sfera di raggioR = ρ⋅N, tangente all’ellissoide nel punto O. Consideriamo lastessa terna euleriana OXYZ e un punto P sfedella sfera avente le stessecoordinate s ed α del punto P elldell’ellissoide.Sulla sfera di raggio R si ha:ρ = N = R α= R e e 2 = 0⎧⎪X⎪⎪⎨Y⎪⎪⎪Z⎩PPPsfesfesfeSlide 1012⎡ s= s⋅sinα⋅ ⎢1−⎣ 6⋅R22⎤ ⎛ s ⎞⎥ = s⋅sinα⋅⎜1−⎟⎦ ⎝ 6⋅ρ⋅N⎠22⎡ s ⎤ ⎛ s ⎞= s⋅cosα⋅ ⎢1−⎥ = s⋅cosα⋅⎜1−⎟2⎣ 6R ⎦ ⎝ 6⋅ρ⋅N⎠22s s= − = −2⋅R2⋅ρ⋅NSviluppi Puiseux-WeingartenTopografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenL’errore che si commette considerando il punto P proiettato sulla sfera diraggio R anziché sull’ellissoide si ottiene dalla differenza delle coordinateeuleriane nelle due ipotesi:⎧⎪X⎪⎪⎨Y⎪⎪⎪Z⎩PPPsfesfesfe- X- Y- ZPPPellellell2 2 22s e ⋅sin α⋅cosϕ= −s⋅sinα⋅ ⋅2 26⋅ρ⋅N1−e⋅sinϕ2s e= s⋅cosα⋅ ⋅6⋅ρ⋅N2s=2⎛⋅⎜⎝1Rα−1 ⎞⎟ρ⋅N⎠222⋅cosα⋅cosϕ21−eSlide 102Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenLe differenze (gli errori) fra le coordinate X Psfeed Y Psfee le coordinateX Pelled Y Pell(quelle che rappresentano la posizione planimetrica delpunto Q) risulteranno massime per ϕ=0 e α=0 o α=π/2.s (in km) 50 100 150 200errore planimetrico assoluto 3.47 27.74 93.62 226.35Δx=Δy (in mm)errore planimetrico relativoΔx/s =Δy/s0.07 x 10 -6 0.28x 10 -6 0.62 x 10 -6 1.13 x 10 -6Scostamenti planimetrici tra ellissoide e sfera localeConsiderando s=100 km tali differenze non superano i 28 mm.Se si tiene presente che nella misura delle distanze si può raggiungere,e limitatamente a qualche decina di chilometri, un precisione relativa di10 -6 (±1mm/1km), tali differenze risultano decisamente inferiori alleincertezze di posizione derivanti dalle misure di distanza.Slide 103Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenMediante le formule di Puiseux-Weingarten è possibile evidenziare che,nei limiti delle approssimazioni fornite dalle operazioni di misura delledistanze e degli angoli, e solo per il posizionamento planimetrico, apparelecito confondere la superficie ellissoidica con una superficie sferica diidentica curvatura totale, applicabile in un punto P, per un intorno di circa100 km dallo stesso punto.La regione entro cui può verificarsi la sostituibilitàrotazione con la sfera locale di raggio:dell'ellissoide diR=a 1−e1−e sen2ρN=2 2ϕprende il nome di campo geodetico e all’interno di questo campo figureellissoidiche possono essere risolte con la trigonometria sferica.Nell'ambito del campo geodetico, si potranno sostituire alle figureellissoidiche le corrispondenti figure sferiche, aventi uguali elementiangolari e lineari, e queste ultime potranno essere risolte con latrigonometria sferica .Slide 104Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenZPsfePer quanto riguarda le quote il discorso è diverso−ZPell=2s2⎛ 1⎜⎝ Rg−1ρN⎞⎟⎠2sρ Ncosϕ ⋅ cos2αQuesta differenza si annulla ai poli (dove tutti i raggi di curvatura sonouguali) e assume i valori massimi, in dipendenza del valore di α,all'equatore.≅2e42Per ϕ=45°, la differenza Z Psfe-Z Pellin funzione della distanza s assumei valori assoluti massimi in corrispondenza di α=0° ed α=90° riassuntinella seguente tabella:s (in km) 1 10 20 50 100⏐Z Psfe - Z Pell ⏐ 0,13 mm 1,3 cm 5,4 cm 0,33 m 1,3 mScostamenti altimetrici tra ellissoide e sfera localeSlide 105Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenPer ϕ = 0°, cioè all'equatore, la differenza Z Psfe-Z Pellrisulta massima:s (in km) 1 10 20 50 100⏐Z Psfe - Z Pell ⏐ cm 0.03 2.66 10.63 66.43 265.72Scostamenti altimetrici tra ellissoide e sfera localeTenuto conto della precisione dei dislivelli ottenuti con la livellazionetrigonometrica, la sfera locale può essere assunta come superficie diriferimento nell'intorno di un punto quando la distanza s tra i punti di cui sicalcola il dislivello non eccede i 15 ÷20 km.Nella livellazione geometrica:si leggono: con stadia graduata al centimetro:si stimano i decimi- i metri- i decimetri --->- i millimetri con stadia graduata al mezzocentimetro:si leggono i decimi e si stimano icentesimiSlide 106Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenSUPERFICIE PIANAConsideriamo sempre la stessa terna euleriana ed un punto P piaappartenente al piano XY ed avente le stesse coordinate s ed α del puntoP elldell’ellissoide.Riscriviamo gli sviluppi di Puiseux-Weingarten tenendo conto che ilraggio di curvatura del piano è infinito e l’eccentricità nulla:⎧X⎪⎨Y⎪⎩ZPPPpiapiapia= s⋅sinα= s⋅cosα= 0Slide 107Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenGli errori che si commettono rispetto all’ipotesi di lavorare nel campogeodetico sono:2⎧s22⎪XP- XP= s⋅sinα⋅a( 1−e ) a( 1−e )pia sfe6⋅ρ⋅Nρ ==2 2 33⎪( 1−e senϕ)W2⎪s⎨Y- Y = s⋅cosαP P⋅pia sfe⎪6⋅ρ⋅Na aN ==2 22⎪1−e sen ϕ Ws⎪ZP- ZP=pia sfe⎩ 2⋅ρ⋅NLe differenze (gli errori) fra le coordinate X Ppiaed Y piae le coordinate X Psfeed Y Psfe(che rappresentano la posizione planimetrica del punto Q)risulteranno massime per ϕ=0, cui corrispondono i valori minimi dei variraggi di curvatura, e per α=0° o 90° gradi.Slide 108Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-Weingartens (in km) 1 10 15 30 50erroreplanimetrico assoluto 0.004 4 14 112 519Δx=Δy (in mm)erroreplanimetrico relativoΔx/s =Δy/s0.004 x 10 -6 0.4 x 10 -6 0.9 x 10 -6 3.7 x 10 -6 10.4 x 10 -6Scostamenti planimetrici tra sfera locale e piano tangenteSiccome la precisione massima di distanziometri EDM è dell'ordine di 1x10 -6, discende quindi che la differenza tra le due coordinate può esseretrascurata a tutti gli effetti in una zona di 15 km di raggio nell’intornodell’origine e in tale intorno si potrà assumere, agli effetti del solo rilievoplanimetrico, come superficie di riferimento il piano tangente all’ellissoidenel punto stesso, utilizzando le note formule della trigonometria piana.Slide 109Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenLe formule di Puiseux-Weingarten evidenziano inoltre che, nei limitidelle approssimazioni fornite dalle operazioni di misura delle distanze edegli angoli, appare lecito confondere la superficie sferica con il suo pianotangente (e quindi è lecito sostituire ad una data figura sferica la suaproiezione sul piano tangente) in una porzione di superficie compresa inun raggio di 15 km circa intorno al punto considerato.La regione entro cui può verificarsi la sostituibilità dell'ellissoide dirotazione con il piano tangente ai fini del solo rilievo planimetrico prende ilnome di campo topografico.Logicamente, riducendo la delimitazione dell'area operativa a quellapropria del campo topografico, le varie elaborazioni di calcolo risulterannotutte ulteriormente semplificate, riducendosi all'applicazione delle relazionidella trigonometria piana.Per l’altimetria non si può definire un campo topografico, poiché l’erroreche si commetterebbe sarebbe sempre maggiore dell’incertezzastrumentale.Occorre tenere conto della curvatura della superficie di riferimento.Slide 110Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Sviluppi Puiseux-WeingartenZPpia−ZPsfe=2s21ρNs [km] 0.1 0.5 1 5 10 15⏐Z Ppia -Z Psfe ⏐ [mm] 0.8 20 80 2000 7800 17757Scostamenti altimetrici tra sfera locale e piano tangenteDalla tabella si constata che:•già a 300 ÷ 350 m dal punto di stazione, l’errore di sfericità nel dislivelloè dell’ordine di 10 mm, paragonabile alla sensibilità del metodo di misuradei dislivelli della livellazione trigonometrica;•poiché si possono misurare, con livellazione geometrica di alta precisione,differenze di quota tra punti distanti 100 m con la precisione del decimo dimillimetro (0,1 mm), si constata che a tale distanza lo scostamento indirezione dell’asse z fra sfera e piano tangente e quindi la differenza Δz, èdell’ordine di 0.8 mm, e quindi l’ipotesi piana del campo topografico per ladeterminazione delle differenze di quota non è lecita.Slide 111Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Influenza della sfericitàInfluenza della sfericità nella misura delle distanze e dei dislivelliin campo topograficoInfluenza della sfericità nella misuradelle distanze in campo topograficoSi consideri il piano tangente alla sferalocale in P o.La differenza Δs tra la distanza s=P oQ e ladistanza s'=P oQ' (con Q' proiezione di Q sulpiano tangente) vale:Δs=s'−s==Rtanω−Rω=R(tanω−ω)Slide 112Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Influenza della sfericitàSviluppando tanω in serie e trascurando i termini del 5° ordine e superiorisi ottiene, ricordando che s = ωR. :332ωωΔs = R(ω + −ω)= R =6 3Il rapporto:Δs =s2s3R23s3Rrappresenta l’errore relativo che sicommette nel sostituire s con s‘.Ricavando s si ottiene:2sΔs= R 3sSlide 113Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Influenza della sfericitàAssegnando a Δs/s il valore della precisione della misura ed assegnandoad R il valore massimo 6378 km si ricava il massimo valore di s, cioèdella distanza entro la quale si può lavorare sul piano tangente.Δss2.10Per esempio, con −6=si ottienes = 15,6 kmSlide 114Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Influenza della sfericitàInfluenza della sfericità nella misura dei dislivelli in campotopograficoIl problema per le quote, anche in questo caso, si pone in modo diverso.Si noti che il sostituire Q con Q’ significacommettere un errore:ΔQ= CQ'−CQ==R2+ s2− R=R(1+sR22−1)In cui è stato sostituito s’ con s in quanto cisi riferisce al campo topografico.Slide 115Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Influenza della sfericitàSviluppando in serie il radicale e trascurando il termine s 4 /8R 4 e quelli diordine superiore, in quanto molto piccoli, si ottiene:ΔQ=R(1+2s2R2−1)=2s2RTale grandezza, sempre positiva, viene detta correzione di sfericità edassume i seguenti valori:s (km) 0,1 0,5 1,0 5,0 10,0ΔQ (m) 0,0008 m 0,02 m 0,08 m 2,0 m 7,8 mPoiché si possono misurare differenze di quota tra punti distanti 100 m conlivellazione geometrica di alta precisione, con la lettura diretta del decimodi mm e la stima del centesimo di mm, si può constatare che se si richiedequesto ordine di precisione non è mai lecito sostituire il piano tangentenelle misure delle quote.Slide 116Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sfericiRISOLUZIONE DI TRIANGOLI SFERICI. TEOREMA DI LEGENDRESia dato un triangolo sferico i cui lati l siano una piccola frazione del raggioR della sfera di appartenenza e si assuma la quantità l/R come quantitàpiccola del primo ordine (10 -2 ).Commettendo un errore dell'ordine di (l/R) 4 ≅ (10 -8 ) gli angoli del triangolopiano, che ha i lati della stessa lunghezza dei lati del triangolo sferico, sipossono derivare dagli angoli del triangolo sferico, sottraendo ad ognunodi essi un terzo dell'eccesso sferico:in quest'ordine di approssimazione i due triangoli sono equivalentiSlide 117Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sfericiIl Teorema di Legendre ci dice che untriangolo sferico, di lati a, b e c edangoli α, β e γ, contenuto nel campogeodetico può essere, ai fini delcalcolo, considerato come un triangolopiano avente i lati uguali a quelli deltriangolo sferico rettificati e gli angolipari a quelli del triangolo sfericodiminuiti ognuno di un terzodell'eccesso sferico.La geometria sferica ci insegna che la somma dei tre angoli α, β e γ èsuperiore a π di una quantità, che denoteremo con 3ε, chiamata eccessosferico:α + β + γ = π + 3εSlide 118Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sfericiL’eccesso sferico, per il Teorema di Cavalieri, è pari al rapporto fral'area del triangolo ed il quadrato del raggio della sfera locale:3 ε =dove S indica l’area del triangolo ed R è il raggio della sfera.SR2Slide 119Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sfericiESEMPIO 8:Di un triangolo sferico A, B, C si conoscono gli archi di geodeticaAC=37956.090mAB=89709.516 me l’angolo in BAC=28°45’42.820’’Si calcolino gli elementi geometrici mancanti sapendo che:ϕ A=43°00’00.000’’λ A=11°52’07.479’’Ed i parametri dell’ellissoide Internazionale o di Hayford sono:a=6378388 me 2 =0.006722670Slide 120Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sferici3 ε =S2Rα =45 42.82028 ° 45'42.820'' = 45° + + = 28°.7618944460 3600AB ⋅ AC ⋅ sinαS ==2819' 198'630.9m2Si calcola il raggio della sfera locale in A:R=ρNSlide 121Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sfericiρ =N =2a( 1−e )2 2( 1−e sen ϕ)32a=Wa=21−e sen ϕ3aW6'378'3880.9984353462( 1−e ) =0.993277330 = 6'365'340.144 m6'378'3880.998435346==236'388'383.609 mR = ρN= 6'376'851. 468 mS3ε= = 0.0000201452Rε = 0°.000384749r= 0°.001154248Calcolo degli elementi mancanti del triangolo:αpiano= α − ε = 28°76150969sferaSlide 122Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sfericiCon il Teorema di Carnot applicato al triangolo piano:BC222= AC + AB − 2 ⋅ AC ⋅ AB ⋅ cosαBC = 59'317.548(45) mAB2=AC2+BC2− 2 ⋅ AC ⋅ BC ⋅ cosγ222AC + BC − ABγ = ar cos= 133°.30651712 ⋅ AC ⋅ BCAC2=AB2+BC2− 2 ⋅ AB ⋅ BC ⋅ cos β22AB + BC − ACβ = ar cos2 ⋅ AB ⋅ BC2= 17°.93197321Verificare quanto vale la somma degli angoli del triangolo piano:α + β + λ = 180°Slide 123Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Triangoli sfericiCalcolo degli elementi sulla sfera:γBC = 59'317.548(45)sferam= γ + ε = 133 ° .3069018 = 133°18'24.846''pianoβsfera= β + ε = 17 ° .93235796 = 17°55'56.489''pianoSlide 124Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Esercizio 1 - geodesiaSull’ellissoide di Hayford si consideri la geodetica uscente con azimut α=60° daun punto di latitudine 43°. Calcolare l’azimut della geodetica in P’ di latitudineφ=44° e P’’ con φ=45°.φW1−e2sin 2ϕP 43° 0.9984353459 4672168.001P’ 44° 0.9983766693 4595688.673P’’ 45° 0.9983179178 4517800.72Per il teorema di Clairaut: r · sinα = cost=4672168.001 · sin 60° = cost → cost = 4046216.18ra ⋅cosϕ=Wα = sin−1costr ϕP’ → α = 61.69517°P’’ → α = 63.58771°Slide 125Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Esercizio 2 - geodesiaDeterminare le coordinate cartesiane geocentriche del punto IGM95 105703 –Cascina di coordinate geografiche WGS84:lat 43° 40’ 29.524’’ lon 10° 34’ 01.239’’ q ell62.04ma WGS84= 6378137 α WGS84= 1/298.257223563ϕ = # ° + # '/60=+λ = # ° + # ' /60 +e222α-α# '' /3600 = 43.6748677 8°# ''/3600= 0.00669437 9992N =aW= 10.5670108 3°=W=6388342.28 1m1−e22sin ϕ =0.99840251 5⎧X=⎪⎨Y=⎪⎩Z=( N + h)( N + h)⋅cosϕ⋅cosλ⋅cosϕ⋅sinλ2( N⋅( 1- e ) + h)= 4542182.68 1m= 847339.830 m⋅sinϕ= 4382077.14 4mSlide 126Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Esercizio 3 - geodesiaIl vertice IGM di M.te Pagliano (1°ordine) ha coordinate su ROMA40:Calcolare nel punto:lat 44° 32’ 21.594’’ lon -5° 00’ 11.276’’a Hayford= 6378388 e 2 Hayford = 0.0067226700221) Raggi principali di curvatura ρ, N.2) Raggio sfera locale R.3) Raggio di curvatura della sezione obliqua di azimut α=45° ed inclinata diβ=60° rispetto alla normale.4) Raggio del paralleloϕ =# °+# '/60+# ''/3600=44.5393316 7°W=1−e2sinϕ =20.99834498 75Slide 127Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa

Esercizio 3 - geodesiaa ⋅=W2( 1- e )ρ3=6367068.64 6mN=aW=6388342.28 1mR=ρ⋅N=6378005.83 5m1Rα=cosρ2α+2sin αN→Rα=N⋅cos2ρ⋅Nα + ρ⋅sin2α=6377996.44 1mRβ= Rα⋅cosβ=3188998.22 1mr= N⋅cosϕ=4553854.75 2mSlide 128Topografia – Corso di Laurea in Ingegneria Civile, dell’Ambiente e del Territorio – Università di Pisa