Teoria Geral de Aletas - Solução unidimensional com área ... - Unesp

Aproximação Unidimensionalpara Condução de Calorem Superfícies EstendidasTransmissão de CalorProf. Dr. Vicente Luiz ScalonProf. Dr. Vicente Luiz Scalonemail: scalon@feb.unesp.brDisciplina: Transmissão de CalorDEM/FEB/UNESP/Bauru

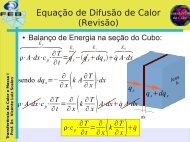
Aproximação Unidimensional deum Problema BidimensionalBalanço energético:h ,T ∞dq convq x dq xTransmissão de CalorProf. Dr. Vicente Luiz Scalon˙ E sq x dq xdq x =dq convĖ=q ex dq convq x dxdq x= d dx −k⋅A sr ⋅dT⋅dxdq conv =h⋅P⋅dx⋅T ∞ −T q xxdxxk e A sr constantes−k⋅A sr⋅ d 2 Tdx 2 =h⋅P⋅T ∞−T d 2 Tdx 2 − h⋅Pk⋅A sr⋅T −T ∞ =0

Condicionando a E.D.O.●para homogeneizar a equação:=T −T ∞ d dx = dTdx d 2 dx = d 2 T2dx 2Transmissão de CalorProf. Dr. Vicente Luiz Scalond 2 Tdx 2 − h⋅Pk⋅A sr⋅T −T ∞ =0d 2 dx 2 −m2 ⋅=0 ou ' '−m 2 ⋅=0d 2 dx 2 − h⋅Pk⋅A sr⋅=0m 2 sendo que:m= h⋅Pk⋅A sr

Solução da E.D.O.' '−m 2 ⋅=0 sendo a solução geral: =A⋅expb⋅xAs derivadas ficam: {'= A⋅b⋅expb⋅x ' '= A⋅b 2 ⋅expb⋅xe na EDO:Transmissão de CalorProf. Dr. Vicente Luiz ScalonA⋅b 2 ⋅expb⋅x−m 2 ⋅A⋅expb⋅x=0 b 2 −m 2 =0 ou b=±mA solução final é resultado da combinação linear das raízes obtidas:=C 1 ⋅expm⋅xC 2 ⋅exp−m⋅xUma solução equivalente em termos de funções hiperbólicas:=C 1 '⋅senhm⋅xC 2 '⋅coshm⋅x

Aplicação de Condição deContorno na paredex=0 T x=0=T b 0=T b −T ∞ = b0=C 1 ⋅expm⋅0C 2 ⋅expm⋅0Transmissão de CalorProf. Dr. Vicente Luiz Scalon b =C 1 C 2(Condição I)0= C 1 ⋅senhm⋅L C 2 ⋅coshm⋅Lx '=L−xA outra solução é utilizada uma orientação := C 1 ⋅senh[m⋅L−x]− C 2 ⋅cosh[m⋅ L−x]x 'x 'x=0 T x=0=T b 0=T b −T ∞ = b b = C 1 ⋅senhm⋅L C 2 ⋅coshm⋅Lx(Condição II)x '

A condição na outra pontaCondições típicas na outra face:Transmissão de CalorProf. Dr. Vicente Luiz Scalon●●●●Aleta muito longaAleta sem troca de calor na ponta (adiabática)Aleta engastada a outra paredeAleta com convecção na ponta

Aleta muito Longax ∞ T ∞=T ∞ ∣ x ∞ =T ∞−T ∞ =0∣ x ∞ =C 1⋅exp∞C2⋅exp−∞ =0 C 1 =0=0Usando este resultado associado à Condição I :Transmissão de CalorProf. Dr. Vicente Luiz Scalon b =C 1 C 2 =C 2 C 2 = bAssim, a solução para o perfil de temperaturas na aleta é: x= b ⋅exp−m⋅x ou T x−T ∞ =T b −T ∞ ⋅exp−m⋅xou ainda: x b= T x−T ∞T b−T ∞=exp−m⋅x

Transmissão de CalorProf. Dr. Vicente Luiz ScalonCalor Dissipado em umaAleta muito LongaO fluxo de calor na aleta respeita a igualdade:Calor que entra pela base por =q dis =Condução' x−k⋅A sr⋅ dTdxCalor queé dissipado porConvecção xLx=0=∫ 0 h⋅P⋅T −T ∞ dxUtilizando o “Calor que entra pela base por Condução”:q dis =−k⋅A sr ' x=0 sendo que ' x=−m⋅ b ⋅exp−m⋅xAssim:q dis=−k⋅A sr⋅−m⋅ b=k⋅A sr⋅ h⋅P ⋅k⋅A b=h⋅P⋅k⋅A sr⋅ bsr

Aleta com ponta adiabáticax=L T ' L=0' L=0usando x= C 1 ⋅senh[m⋅ L−x] C 2 ⋅cosh[m⋅ L−x] ' x=−m⋅{C 1 ⋅cosh[m⋅ L−x] C 2 ⋅senh[m⋅ L−x]}Assim ' L=−m⋅[ C 1 ⋅cosh0 C 2 ⋅senh 0]=−m⋅C 1 C 1 =0Transmissão de CalorProf. Dr. Vicente Luiz ScalonUtilizando a Condição II: b = C 2 ⋅coshm⋅L C 2 =A solução final fica: x b bcoshm⋅L= T x−T ∞T b−T ∞=cosh[m⋅ L−x]coshm⋅L

Calor Dissipado numaAleta com ponta adiabáticaTransmissão de CalorProf. Dr. Vicente Luiz ScalonNovamente o “Calor que entra pela base por Condução” é:q dis =−k⋅A sr ' x=0sendo que ' x=−m⋅{bcoshm⋅L ⋅senh[m⋅L−x] }que substituída na equação acima:q dis=k⋅A sr⋅ h⋅P ⋅{ bk⋅A sr coshm⋅L ⋅senhm⋅L }Rearranjada, esta equação fica:q dis=h⋅P⋅k⋅A sr bsenhm⋅Lcoshm⋅L = h⋅P⋅k⋅A sr btanh m⋅L

Aleta engastada em outraparede com temperaturaconhecidax=L T L=T L L=T L −T ∞ = Lusando x=L= C 1 ⋅senh0 C 2 ⋅cosh0 C 2 = LTransmissão de CalorProf. Dr. Vicente Luiz ScalonUtilizando a Condição II: b = C 1 ⋅senhm⋅L L ⋅coshm⋅L x bou x b= T x−T ∞T b −T ∞ C 1 = b− L ⋅coshm⋅Lsenhm⋅L= 1− L/ b ⋅cosh m⋅L⋅senh [m⋅ L−x] L⋅cosh[m⋅ L−x]senhm⋅L b= L/ b senhm⋅xsenh[m⋅ L−x]senhm⋅L

Fluxo de Calor emAleta EngastadaTransmissão de CalorProf. Dr. Vicente Luiz ScalonNovamente o “Calor que entra pela base por Condução” é:q dis =−k⋅A sr ' x=0⋅{sendo ' x=m⋅ L/ b coshm⋅x−cosh[m⋅ L−x]}bsenhm⋅Lque substituída na equação acima:q dis =−k⋅A sr⋅ h⋅P ⋅{ L/ b −coshm⋅L}k⋅A srsenhm⋅LRearranjada, esta equação fica:q dis =h⋅P⋅k⋅A sr b[ coshm⋅L− L/ bsenhm⋅L ]

Aleta com Convecção na pontaTransmissão de CalorProf. Dr. Vicente Luiz Scalonx=L −k⋅T ' L=h⋅T L −T ∞ −k⋅ ' L=h⋅ L k⋅m⋅C 1 =h⋅C 2 C 1= hm⋅k ⋅ C 2Utilizando a Condição II: b = C 2 ⋅[Assim x= T x−T ∞= b T b−T ∞hm⋅k senhm⋅Lcoshm⋅L ] b C 2 =h/m⋅k senhm⋅Lcoshm⋅Lh/m⋅k ⋅cosh [m⋅L−x]senh[m⋅L−x]h/m⋅k senhm⋅Lcosh m⋅L

Calor Dissipado porAleta com Convecção na pontaTransmissão de CalorProf. Dr. Vicente Luiz ScalonNovamente o “Calor que entra pela base por Condução” é:q dis =−k⋅A sr ' x=0sendo ' x=−m⋅ b ⋅{que substituída na equação acima:q dis=k⋅A sr⋅ h⋅P ⋅[ k⋅A sre rearranjada, esta equação fica:b[q dis =h⋅P⋅k⋅A sr h/m⋅k ⋅cosh [m⋅L−x]sinh [m⋅L−x]h/m⋅k senhm⋅Lcosh m⋅L }h/m⋅k ⋅coshm⋅Lsinhm⋅L]h/m⋅k senhm⋅Lcoshm⋅Lh⋅coshm⋅Lsinhm⋅L]m⋅kh⋅senhm⋅Lcoshm⋅L m⋅k