Föreläsning 4

23
4. Differentialkalkyl
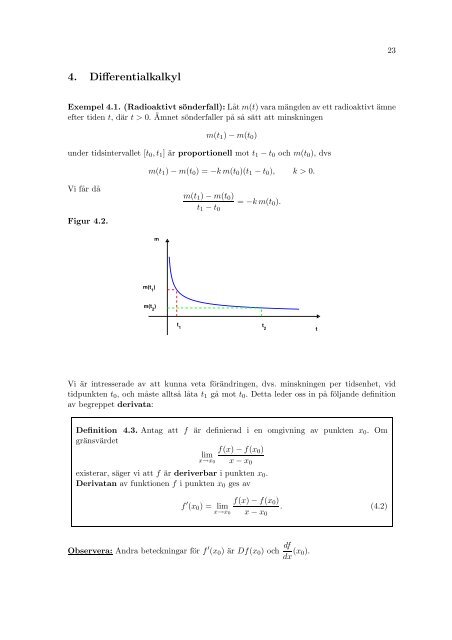
Exempel 4.1. (Radioaktivt sönderfall): Låt m(t) vara mängden av ett radioaktivt ämne
efter tiden t, där t > 0. Ämnet sönderfaller på så sätt att minskningen
m(t 1 ) − m(t 0 )
under tidsintervallet [t 0 ,t 1 ] är proportionell mot t 1 − t 0 och m(t 0 ), dvs
m(t 1 ) − m(t 0 ) = −k m(t 0 )(t 1 − t 0 ), k > 0.
Vi får då
Figur 4.2.
m(t 1 ) − m(t 0 )
t 1 − t 0
= −k m(t 0 ).
m
m(t 1
)
m(t 2
)
t 1 t 2
t
Vi är intresserade av att kunna veta förändringen, dvs. minskningen per tidsenhet, vid
tidpunkten t 0 , och måste alltså låta t 1 gå mot t 0 . Detta leder oss in på följande definition
av begreppet derivata:
Definition 4.3. Antag att f är definierad i en omgivning av punkten x 0 . Om
gränsvärdet
f(x) − f(x 0 )
lim
x→x 0 x − x 0
existerar, säger vi att f är deriverbar i punkten x 0 .
Derivatan av funktionen f i punkten x 0 ges av
f ′ (x 0 ) = lim
x→x 0
f(x) − f(x 0 )
x − x 0
. (4.2)
Observera: Andra beteckningar för f ′ (x 0 ) är Df(x 0 ) och df
dx (x 0).

24 4 DIFFERENTIALKALKYL
Geometrisk tolkning av derivatan: Låt P 0 = (x 0 ,f(x 0 )) och P = (x,f(x)) vara två
punkter på kurvan y = f(x):
Figur 4.4.
y
y = f(x)
L 1
x 1
− x 0
f(x 1
) − f(x 0
)
x 0
x 1
x
Differenskvoten f(x) − f(x 0)
är riktningskoefficienten för sekanten P 0 P. Om f är deriverbar
i x 0 , har riktningskoefficienten ett gränsvärde, då x → x 0 . Detta innebär att sekanten
x − x 0
närmar sig en linje genom P 0 med riktningskoefficient f ′ (x 0 ), då x → x 0 . Denna linje kallas
tangenten i P 0 .
Definition 4.5. Tangenten till kurvan y = f(x) i punkten P 0 = (x 0 ,f(x 0 )) är linjen
y = f(x 0 ) + f ′ (x 0 )(x − x 0 ).
Normalen i punkten P 0 = (x 0 ,f(x 0 )) är linjen
Figur 4.6.
y
y = f(x 0 ) − 1
f ′ (x 0 ) (x − x 0).
L 1
x x 2 1
y = f(x)
x 0
x
L 2
Tangent

25
En omskrivning av derivatans definition i Definition 4.2 visar hur viktigt det är att kunna
standardgränsvärdena:
Definition 4.7. Antag att f är deriverbar i punkten x 0 . Låt h = x − x 0 . Då gäller att
x = x 0 + h och
f ′ f(x 0 + h) − f(x 0 )
(x 0 ) = lim
.
h→0 h
Exempel 4.8. Använd definitionen av derivata för att bestämma f ′ (x) då f(x) = 1 x 2.
Lösning:
Exempel 4.9. De elementära funktionerna e x , sin x och ln x är deriverbara.
Lösning:

26 4 DIFFERENTIALKALKYL
Sats 4.10. Antag att f(x) och g(x) är deiverbara. Då gäller att
1. (C f) ′ (x) = C f ′ (x), där C är en konstant.
2. (f + g) ′ (x) = f ′ (x) + g ′ (x)
3. (fg) ′ (x) = f ′ (x)g(x) + f(x)g ′ (x), produktregeln
4.
( ) f ′
(x) = f ′ (x)g(x) − f(x)g ′ (x)
g
g 2 , kvotregeln
(x)
Bevis:
Exempel 4.11. Derivera funktionerna f(x) = x2 + 1
x − 3 och g(x) = ex sin x.
Lösning:

27
Nästa sats visar hur vi deriverar sammansatta funktioner:
Sats 4.12. (Kedjeregeln): Låt g : A ↦→ B och f : B ↦→ C vara två deriverbara
funktioner. Då gäller att den sammansatta funktionen h(x) = f(g(x)) ∈ C, där x ∈ A
är deriverbar och
h ′ (x) = f ′ (g(x))g ′ (x).
Bevis:
Exempel 4.13. Vi har i Exempel 4.9 visat att e x , sinx och ln x är deriverbara. Nedan visar
vi att cos x och x α också är deriverbara.
Lösning:
Exempel 4.14. Derivera a) (5x + 1) 8 b) e√ x+lnx
e) ln( √ x 2 + 1 − x)
Lösning:

28 4 DIFFERENTIALKALKYL
Nästa sats visar vilket samband som råder mellan deriverbarhet och kontinuitet:
Sats 4.15. Om f är deriverbar i x så är f även kontinuerlig i x.
Bevis:
Innan vi tar upp Exempel 4.17 nedan som visar att omvändningen inte är sann, d.v.s. om
f är kontinuerlig i x så behöver f inte vara deriverbar i x, tar vi och tittar närmare på
definition av derivatan. Vi börjar med följande definition:
Definition 4.16. Gränsvärdena (om de existerar)
f + ′ (x) = lim
f(x + h) − f(x)
h→0 + h
, f − ′ f(x + h) − f(x)
(x) = lim
h→0 − h
kallas f:s höger- respektive vänster derivata i punkten x.
Enligt gränsvärdesdefinitionen följer att en funktionen f är deriverbar i punkten x med
derivatan f ′ (x) om och endast om f + ′ (x) och f − ′ (x) existera och är lika, dvs
f ′ +(x) = f ′ −(x).
Då ges derivatan f ′ (x) av
f ′ +(x) = f ′ (x) = f ′ −(x).
Exempel 4.17. Är f deriverbar om f(x) =
{ x 2 , x ≤ 1
x, x > 1 ?
Lösning:

29
Definition 4.18. Funktionen f säges vara deriverbar i ett intervall I om den är deriverbar
i varje punkt som tillhör I (höger- och vänster derivator i eventuella ändpunkter
till I). Funktionen x ↦→ f ′ (x) kallas derivatan av f.
Exempel 4.19. Att funktionen f är deriverbar på I = [a,b] betyder att f är deriverbar på
]a,b[ och att f + ′ (a) och f − ′ (b) existerar.
Exempel 4.20. Bestäm a och b så att funktionen
{ ae x + bx + x 2 , x ≤ 0
f(x) = √
x + 4, x > 0
blir deriverbar.
Lösning:
Figur 4.21.

30 5 IMPLICIT DERIVERING OCH DERIVATA AV INVERSA FUNKTIONER
5. Implicit derivering och derivata av inversa funktioner
Vi har hittills deriverat y med avseende på x, där y ges som en funktion av x, dvs y = f(x).
I många tillämpningar är sambandet mellan x och y mer komplicierat än så. Ett mer naturligt
samband är då F(x,y) = 0. Att derivera y i ett sådant samband kallas implicit
deriverng. Exemplen nedan visar hur en sådan derivering går till.
Exempel 5.1. En polisman står nära en motorväg och övervakar hastigheten med hjälp av
radar enligt figuren nedan:
Lösning:
Exempel 5.2. Sambandet x 3 + y 3 − 9xy = 0 definierar en kurva y = y(x) i närheten av
punkten (2,4). Bestäm tagnenten till kurvan i punkten (2,4).
Lösning:

5.1 Derivata av invers funktion 31
5.1. Derivata av invers funktion
I det här avsnittet kommer vi att bestämma derivatan till inversen till en godtycklig deriverbar
och inverterbar funktion. Vi kommer också att titta speciellt på derivatan av arcusfunktionerna
som är inverser till de trigonometriska funktionerna.
Sats 5.3. (Satsen om derivatan av invers): Antag att f och dess invers f −1 är
deriverbara funktioner. Då gäller att
(f −1 ) ′ (b) = 1
f ′ , där b = f(a).
(a)
Bevis: Enligt kedjeregeln får vi om vi deriverar båda leden i
x = f −1 (f(x))
att
dvs
om vi sätter
1 = (f −1 ) ′ (f(x))f ′ (x),
(f −1 ) ′ (y) = 1
f ′ (x)
y = f(x).
Exempel 5.4. Bestäm (f −1 ) ′ (5) om f(x) = x 5 + x 3 + 3x.
Lösning:

32 5 IMPLICIT DERIVERING OCH DERIVATA AV INVERSA FUNKTIONER
Nedan använder vi resultatet i Sats 5.3 för att härleda derivatan av arcusfunktionerna.
Sats 5.5. (Derivata av arcusfunktionerna):
1. Om f(x) = sin x, − π 2 ≤ x ≤ π 2 , så är f −1 (x) = arcsin x, −1 ≤ x ≤ 1 och
(f −1 ) ′ (x) =
1
√ , −1 < x < 1.
1 − x 2
2. Om f(x) = cos x, 0 ≤ x ≤ π, så är f −1 (x) = arccos x, −1 ≤ x ≤ 1 och
(f −1 ) ′ 1
(x) = −√ , −1 < x < 1.
1 − x 2
3. Om f(x) = tan x, − π 2 < x < π 2 , så är f −1 (x) = arctan x, −∞ < x < ∞ och
(f −1 ) ′ (x) = 1
1 + x2, −∞ < x < ∞.
Bevis:
1. Vi vet att y = arcsin x, −1 ≤ x ≤ 1 ⇔ sin y = x − π 2 ≤ y ≤ π 2 .
Deriverar vi nu y i andra likheten i ovan med avseende på x, där vi samtidigt tar
hänsyn till inre derivatan y ′ , får vi
y ′ cos y = 1 ⇔ y ′ = 1
cos y = 1
± √ 1 − sin 2 y = 1
± √ 1 − x 2.
Eftersom cos y > 0 för − π 2 < y < π 2 följer att y′ =
(f −1 ) ′ (x) =
1
√
1 − x 2 , dvs
1
√ , −1 < x < 1.
1 − x 2
2. Bevisas på samma sätt som 1.
3. Eftersom
d
dx tan x = d
dx
sin x
cos x = sin2 x + cos 2 x
cos 2 x
= cos2 x
cos 2 x + sin2 x
cos 2 x = 1 + tan2 x,
får vi om vi deriverar y = arctan x, −∞ < x < ∞, dvs tan y = x, − π 2 < y < π 2 att
y ′ (1 + tan 2 y) = 1 ⇔ y ′ =
1
1 + tan 2 y = 1
1 + x2, −∞ < x < ∞.

5.1 Derivata av invers funktion 33
Exempel 5.6. Derivera f(x) = arcsin 4x och g(x) = arctan ln x.
Lösning: