5.1.6 Delo virtualnih napetosti v linearno elasticnih vzmeteh - FGG-KM

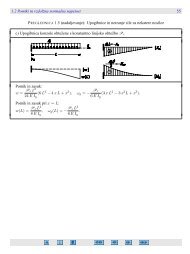
5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 415
Slika 5.43: Osna sila in upogibni moment zaradi virtualne sile δF z
Navpični pomik v točki E določimo z integracijo enačbe
w E = ∑ ∫ (
Nx δ ¯N x
+ M y δ ¯M )
y
dx =
E A x E I y
el
Li
(
= 1 1 · 100 · 100 + 75 · √2
· 50 √ √
2
2
E A x 2 + 25 · √2
· 50 √ √
2
2
2 + 75 · √2
· 50 √ 2 · √2
)
+
(
+ 1 2500 · 50 · √2 )
· 2
E I y 2 3 · 50 · 2 = 0.0031 + 2.7203 = 2.7 cm.
Relativni vpliv osnih sil na pomik v točki E je zelo majhen, saj znaša le 0.12 % od skupnega pomika.
Pomik v točki E se zgodi skoraj izključno zaradi upogibanja nosilcev, medtem ko je vpliv osnih deformacij
zanemarljiv. Zato pri računu velikokrat vpliv osnih sil na pomike zanemarimo.
Primer 5.10 Konzola je sestavljena iz petih lesenih desk debeline 2 cm in širine 10 cm. V prvem primeru
so deske postavljene vodoravno, v drugem pa navpično (slika 5.44). Izračunajmo največjo normalno
napetost σ xx,max v konzoli! Točkovna sila na koncu konzole, katere vpliv se enakomerno razdeli na vseh
pet desk, je enaka 1 kN. Dolžina konzole je enaka L = 1 m. Izračunajmo tudi poves prostega konca
konzole! Elastični modul je E = 2000 kN/cm 2 . Vpliv prečnih sil zanemarimo!
Slika 5.44: Konzolo sestavlja pet desk, ki so položene vodoravno oziroma navpično

416 5 Uporaba izreka o virtualnih silah
Račun največje normalne napetosti
Največjo normalno napetost v konzoli izračunamo z enačbo
σ xx,max = |M y| max
I y
|z| max = F L |z| max
I y
.
Če so deske položene vodoravno, je največja normalna napetost enaka
Upoštevali smo, da je
σ a xx,max = 1 · 100 · 1
5 · 6.66 = 3 kN/cm2 .
I y1 =
10 · 23
12
= 6.66 cm 4 , I y = 5 I y1 |z| max = 1 cm.
Za navpično položene deske je največja normalna napetost bistveno manjša kot v primeru vodoravno
položenih desk
σ b xx,max = 1 · 100 · 5
5 · 166.66 = 0.6 kN/cm2 .
Upoštevali smo
I y1 = 2 · 103
12
= 166.66 cm 4 , I y = 5 I y1 , |z| max = 5 cm.
Razmerje med največjimi normalnimi napetostmi za oba primera je
σ a xx,max
σ b xx,max
= 3
0.6 = 5.
Če deske postavimo navpično, so pri isti obtežbi napetosti 5 krat manjše.
Račun povesa prostega konca konzole
Na prostem koncu konzole postavimo virtualno silo δF = 1, ki deluje v smeri osi z.
izračunamo po enačbi
w T =
∫ L
0
M y δ ¯M y
E I y
Diagrama upogibnih momentov M y in δ ¯M y prikazujemo na sliki 5.45.
dx.
Pomik w T

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 417
Slika 5.45: Upogibni moment M y zaradi sile F in zaradi virtualne sile δF = 1
Pomik w T izračunamo z integracijo produkta M y δ ¯M y po enačbi (5.24)
w T = 1
E I y
F L L 2
Pomik na koncu vodoravno položenih desk je
w a T =
2 L
3 = F L3
3 E I y
.
1 · 100 3
3 · 2000 · 5 · 6.66 = 5 cm.
Če so deske položene navpično, je pomik bistveno manjši
Razmerje med pomikoma je
w b T =
1 · 100 3
= 0.2 cm.
3 · 2000 · 5 · 166.66
wT
a
wT
b
= 25.
Če deske postavimo navpično, je pomik 25 krat manjši, kot če jih postavimo vodoravno. Vidimo, da
je navpična postavitev ugodnejša tako glede na največje napetosti, kot tudi glede na pomik na koncu
konzole.
Primer 5.11 S prikazano napravo merimo silo F , ki se preko vijaka B prenaša na preizkušanec A (slika
5.46). Silo merimo z velikostjo pomika jeklenega nosilca D–D v točki E. Sila se na nosilec D–D prenaša
preko togega nosilca K–K. Določimo razdaljo a od podpore D do prijemališča sile K na nosilec D–D,
da bo pri sili F = 5 kN upogib nosilca v točki E enak 1 mm? Nosilec D–D ima širino 6 cm, višino
4 cm, dolžino 1 m, modul elastičnosti materiala pa je 20000 kN/cm 2 .

418 5 Uporaba izreka o virtualnih silah
Slika 5.46: Velikost sile izračunamo iz velikosti pomika nosilca D–D v točki E
Računski model ter diagrama upogibnih momentov zaradi sile F in virtualne sile δF z = 1 prikazujemo
na sliki 5.47.
Slika 5.47: Diagram upogibnega momenta v nosilcu D–D zaradi sil F/2 in δF = 1
Pomik w T na sredini nosilca D–D določimo z enačbo
Za obravnavani primer dobimo:
w T =
∫ L
0
M y δ ¯M y
E I y
dx.
E I y w T = 2 F a
2
a
2
2
3
a
2 + 2 1 ( a
2 2 + L ) ( ) L F a
4 2 − a a3
= −F
2 12 + F L2 a
16 .
Iz zadnje enačbe moramo določiti a, zato jo preoblikujemo takole:
a 3 − 3 4 L2 a + 12
F E I y w T = 0.

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 419
Vztrajnostni moment pravokotnega prečnega prereza nosilca D–D je
Ob upoštevanju podatkov dobimo
I y = 6 · 43
12 = 32 cm4 .
a 3 − 3 4 1002 a + 12
5 2 · 104 · 32 · 0.1 = 0 → a 3 − 7500 a + 153600 = 0.
To nelinearno enačbo rešimo numerično in dobimo a = 21.8758 cm. Uporabimo lahko različne programe
(Mathematica, Matlab, Excel, . . .) †
Primer 5.12 Določimo navpični pomik točke D statično določene konstrukcije na sliki 5.48! Velikost
sile je F = 10 kN, modul elastičnosti materiala je E = 20000 kN/cm 2 . Pri računu upoštevajmo tudi
vpliv osnih sil na deformiranje konstrukcije. Dimenzije konstrukcije prikazujemo na sliki 5.48.
Slika 5.48: Geometrijski podatki o konstrukciji ter lega in smer sile F
Enačbo za računanje pomika oziroma zasuka smo izpeljali ob predpostavki, da sta osi y in z glavni
vztrajnostni osi v težišču prečnega prereza. V obravnavanem primeru glavni vztrajnostni osi oklepata z
osema y in z kot 45 ◦ , saj tudi simetrijska os prereza oklepa z osema y in z kot 45 ◦ . Če želimo nalogo
rešiti, moramo izračunati upogibne momente glede na glavni vztrajnostni osi.
Osno silo in upogibni moment glede na os y zaradi sile F prikazujemo na sliki 5.49.
† Ničle polinoma, določene z računalniškim programom Mathematica:
FindRoot[a^3-7500a+153600==0,{a,25}]
{a -> 21.8758}

420 5 Uporaba izreka o virtualnih silah
Slika 5.49: Osna sila in upogibni moment glede na os y
V točko D postavimo virtualno silo δF = 1, ki deluje v enaki smeri, kot sila F . Podobno izračunamo
diagrama δN x in δ ¯M y zaradi sile δF z = 1 (slika 5.50).
Slika 5.50: Osna sila in upogibni moment glede na os y zaradi δF z = 1
Glavni vztrajnostni osi η in ζ sta glede na os y zasukani za 45 ◦ oziroma 225 ◦ . Upogibni moment zaradi
sile F glede na ti osi dobimo tako, da M y projiciramo na osi η in ζ (slika 5.51).
Slika 5.51: Upogibni moment moramo izračunati glede na glavni vztrajnostni osi η in ζ
V tem primeru izračunamo pomik w D po enačbi
w D =
∫ L
0
(
Nx δ ¯N x
E A x
+ M η δ ¯M η
E I η
+ M ζ δ ¯M ζ
E I ζ
)
dx.

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 421
Geometrijske lastnosti prečnega prereza so:
A x = 69 cm 2 , I y = I z = 995.663 cm 4 , I yz = 551.087 cm 4 ,
tg2 α g =
2 I yz
= ∞ → α g = 45 ◦ ,
I y − I z
I η = 1546.750 cm 4 , I ζ = 444.576 cm 4 .
Upogibna momenta v točki D glede na osi η in ζ sta:
M η = M y cos 45 ◦ = 1414 kNcm,
M ζ = −M y cos 45 ◦ = −1414 kNcm.
Diagrama M η in M ζ zaradi sile F ter δ ¯M η in δ ¯M ζ zaradi sile δF z = 1 prikazujemo na sliki 5.52.
Slika 5.52: Upogibna momenta M η in M ζ ter δ ¯M η in δ ¯M ζ (v kNcm)
Pomik w D je:
w D = 1 (10 · 200 · 1 · 2) + 1 ( 1414 · 200
· 2 )
E A x E I η 2 3 · 141.4 · 2 +
+ 1 ( 1414 · 200
· 2 )
E I ζ 2 3 · 141.4 · 2 = 0.0029 + 0.8620 + 2.9991 = 3.86 cm.
Tudi v tem primeru je del pomika zaradi osne deformacije zelo majhen v primerjavi z delom zaradi
upogiba, saj znaša le 0.075% skupnega pomika.

422 5 Uporaba izreka o virtualnih silah
Primer 5.13 Določimo diagrame notranjih sil ter navpični pomik točke C za konstrukcijo na sliki 5.53!
Velikost sile F je 10 kN, razdalja a je enaka 10 m. Količine E, I y in A x so konstante. Upoštevajmo tudi
vpliv osnih sil na pomike!
Slika 5.53: Ker sila F ni v vozlišču, v delu CB nastopijo tudi upogibni momenti in prečne sile
Konstrukcija je statično določena. Reakcije izračunamo iz ravnotežnih pogojev. Notranje sile izračunamo,
če konstrukcijo razdelimo na dva dela in upoštevamo, da sta v palicah od nič različni le osni sili N AB in
N AC (slika 5.54).
Slika 5.54: Za račun notranjih sil konstrukcijo razdelimo na dva dela
Reakcije in osni sili so:
A x = 7.071 kN, A z = −3.536 kN,
B z = −3.536 kN,
N AB = −3.536 kN, N AC = −5 kN.
Diagrame notranjih sil zaradi zunanje sile F prikazujemo na sliki 5.55.

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 423
Slika 5.55: Osna sila, prečna sila in upogibni moment zaradi sile F
Na sliki 5.56 prikazujemo notranje sile zaradi virtualne sile δF z = 1.
Slika 5.56: Notranje sile zaradi sile δF z = 1
Ker so od nič različne notranje sile zaradi virtualne obtežbe le osna sila (slika 5.56), navpični pomik
prijemališča sile F izračunamo po poenostavljeni enačbi
Za obravnavani primer dobimo:
w C =
∫ L
0
N x δ ¯N x
dx.
E A x
w C = 1
E A x
(
5 · a √ 2 ·
√
2
2 − √
2
2 · 5 · 2 a · 0.5 )
= 14.645
E A x
.

424 5 Uporaba izreka o virtualnih silah
Primer 5.14 Določimo največji poves na sliki 5.57 prikaznega nosilca! Modul elastičnosti E je 210 GPa.
Slika 5.57: Prečni prerez nosilca ni povsod enak
Zaradi simetrične obtežbe je vodoravna reakcija v levi podpori enaka nič. Zato so simetrične tudi reakcije
in lahko rečemo, da sta simetrični tako obtežba kot oblika konstrukcije. Največji pomik nastane na sredini
konstrukcije. Izračunamo ga po enačbi
w =
∫ L
0
M y δ ¯M y
dx,
E I y
kjer smo vpliv prečnih sil zanemarili. Izračunati moramo vztrajnostna momenta za oba prečna prereza
in
I y1 =
25 · 523
12
−
24.1 · 503
12
= 41891.67 cm 4
( )
20 · 0.8
3
I y2 = I y1 + 2 + 26.4 2 · 20 · 0.8 = 64196.09 cm 4 .
12

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 425
Na sliki 5.58 prikazujemo diagrama upogibnih momentov zaradi zunanje obtežbe in zaradi virtualne sile
δF z = 1, ki jo postavimo na sredino nosilca, saj je zaradi simetrije pomik tam največji.
Slika 5.58: Upogibni moment zaradi zunanje obtežbe in zaradi virtualne sile δF z = 1
Upogibna momenta na sliki 5.58 sta zapisana v kNcm, zato tudi elastični modul zapišimo v ustreznih
enotah E = 210 GPa = 210 GN/m 2 = 210 · 10 6 kN/(10 4 cm 2 ) = 21000 kN/cm 2 .
Največji navpični pomik izračunamo
w = 1 ( 240 · 24000
E I y1 2
120 · 36000
+
2
=
· 2 )
3 · 120 · 2 + 1 [ ( 120 · 24000 2
E I y2 2 3 · 120 + 1 )
3 · 180 · 2+
(
180 + 230 ) ]
· 2 =
2
( 1
3 · 120 + 2 3 · 180 )
· 2 + 100 · 36000
4.608 · 10 8 2.5704 · 109
+ = 0.524 + 1.907 = 2.43 cm.
21000 · 41891.67 21000 · 64196.09
Primer 5.15 Določimo največji pomik in največjo vzdolžno normalno napetost na sliki 5.59 prikazanega
nosilca! Posebnost obravnavanega nosilca je, da se širina pravokotnega prečnega prereza na delu
nosilca linearno spreminja. Pomik določimo z uporabo izreka o virtualnih silah. Sila in modul elastičnosti
sta F = 100 N in E = 21000 kN/cm 2 .
Slika 5.59: Širina nosilca se na delu nosilca linearno spreminja

426 5 Uporaba izreka o virtualnih silah
Zaradi simetrije nosilca in obtežbe dobimo največji pomik na sredini nosilca pri x = 1.0 m. Funkciji
M y in δ ¯M y sta simetrični, zato je
w = 2
∫L/2
0
M y δ ¯M y
E I y
dx, I y = I y (x)
Upogibna momenta na levi polovici nosilca zaradi zunanje in virtualne obtežbe sta
Vztrajnostna momenta sta
M y = F 2 x, δ ¯M y = x 2 .
0 ≤ x ≤ 50 : I y =
5.5 · 13
,
12
50 ≤ x ≤ 100 : I y = b(x)13
12
= 5.5 x
12 · 50 ,
saj se širina nosilca vzdolž osi x spreminja po naslednji enačbi (slika 5.60):
y
x − 50 = 2.75
50 , y = 2.75
50
(x − 50), b(x) = 5.5 + 2 y =
5.5 x
50 .
Slika 5.60: Širina nosilca se za 50 ≤ x ≤ 100 linearno spreminja
Pomik točke C je
w = 2
∫ 50
0
F x
2
x
2
∫100
12
5.5 E dx + 2
50
F x
2
x 12 · 50
2 5.5 x E dx =
= 6 F
5.5 E · 1
3 · 503 + 300 F
5.5 E · 1
2 · (1002 − 50 2 ) = 0.22 + 0.97 = 1.19 cm.
Največjo normalno napetost določimo ločeno za oba intervala. Na intervalu 0 ≤ x ≤ 50 cm mesto
največje normalne napetosti sovpada z mestom največje upogibne napetosti
σ xx,max = M y,max
z max = F x max12
· 0.5
I y
2 · 5.5

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 427
Pri x = 50 cm dobimo:
x = 50cm : σ xx,max =
0.1 · 50 · 12
2 · 5.5
· 0.5 = 2.73 kN/cm 2 .
Na intervalu 50 ≤ x ≤ 100 cm napetosti določimo tako, da v izraz za normalne napetosti vstavimo
izraza za M y in I y , medtem ko je z max konstanten (z max = 0.5 cm):
σ xx,max = F x 12 · 50 0.1 · 12 · 50 · 0.5
· 0.5 = = 2.73kN/cm 2 .
2 5.5 x 11
Napetost σ xx se na intervalu 50 ≤ x ≤ 100 ne spreminja.
Primer 5.16 Listnata vzmet ima enako robno napetost v vseh prerezih in predstavlja nosilec idealne
oblike glede robnih normalnih napetosti. Na sliki 5.61 je sestavljena iz 10 trakov širine 7.5 cm in
debeline 10 mm. Dolžina vzmeti L = 100 cm, dopustna normalna napetost σ xx,dop = 40 kN/cm 2 .
Jeklo vzmeti ima modul elastičnosti E j = 20000 kN/cm 2 . Določimo nosilnost vzmeti (dopustno silo
F ) ter upogib w F na sredini razpona zaradi sile F ! Pri računu zanemarimo začetno ukrivljenost osi
nosilca, ki je računski model vzmeti, ter trenje med listi vzmeti.
Slika 5.61: Listnata vzmet sestavljena iz 10 listov
Računski model prikazujemo na sliki 5.62.

428 5 Uporaba izreka o virtualnih silah
Slika 5.62: Računski model listnate vzmeti
Pokažimo, da največja vzdolžna normalna napetost σ xx ni odvisna od koordinate x.
b(x) = 2 b
L x,
W y = y h2
6 , σ xx,max = M y(x)
W y (x) = A x 6 L
2 b x h 2 = 6 A L
2 b h 2 = M y(L/2)
W y (L/2) .
Če ploščo na sliki 5.62 razrežemo in trakove položimo kot kaže slika 5.63, dobimo listnato vzmet.
Slika 5.63: Vztrajnostni moment in napetost σ xx se ne spremenita, če ploščo razrežemo in liste
položimo, kot kaže slika
Dopustna sila
Dopustno silo izračunamo iz enačbe za določitev normalne napetosti:
σ xx (x) = σ xx (L/2) ≤ σ xx,dop → M y(L/2)
W y (L/2) ≤ σ xx,dop.

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 429
Iz slike 5.63 vidimo, da je največja širina b računskega modela vzmeti enaka b = 10 · 7.5 = 75 cm.
Širina nosilca se vzdolž osi spreminja po enačbi b(x) = 2 b x/L. Ker je
M y (L/2) = F L
4 , W y(L/2) = b h2
6 ,
sledi
F ≤ 2 b h2 σ xx,dop
3 L
Navpični pomik na sredini razpona
= 2 · 75 · 12 · 40
3 · 100
= 20 kN.
Pomik določimo po enačbi
w F =
Diagrama M y in δ ¯M y prikazujemo na sliki 5.64.
∫ L
0
M y δ ¯M y
E I y
dx.
Slika 5.64: Upogibna momenta M y in δ ¯M y
Zaradi simetrije diagramov in konstantnega materiala lahko zapišemo
w F = 2 E
∫L/2
0
M y δ ¯M y
I y
Ker se prečni prerez vzdolž osi x spreminja, zapišemo integrand v odvisnosti od spremenljivke x in ga
integriramo. Ker je
sledi
Po integriranju dobimo
dx.
M y (x) = F x
2 , δM y(x) = x 2 , I b(x) h3
y(x) =
12
w F = 2 E
∫L/2
0
F x
2
w F = 3 F L3
8 b h 3 E
x
2
6 L
b H 3 x dx = F ∫L/2
3 L
E b h 3
0
= b h3 x
6 L ,
x dx
=
3 · 20 · 1003
8 · 75 · 1 3 · 20000 = 5 cm.

430 5 Uporaba izreka o virtualnih silah
Primer 5.17 Konstrukcija na sliki 5.65 je sestavljena iz dveh elementov z odprtim tankostenskim prečnim
prerezom. Določimo velikost sile F tako, da bo največja strižna napetost enaka dopustni strižni napetosti
τ dop = 10 kN/cm 2 . Določimo tudi, za koliko se sila F lahko poveča, če stik zavarimo tako, da dobimo
elementa z zaprtim tankostenskim prerezom. Pri tem predpostavimo, da nastane v elementih enakomerna
torzija. Izračunajmo tudi navpični pomik w C točke C za sili, ki ustrezata odprtemu oziroma zaprtemu
prečnemu prerezu. Elastični modul E materiala je 24000 kN/cm 2 , strižni modul G je 10000 kN/cm 2 ,
vztrajnostni moment I y2 elementa 2 je 5000 cm 4 , dolžina L = 1.5 m in dolžina a = 0.5 m. Zunanji
premer D prečnega prereza je 30 cm, debelina t stene prečnega prereza pa 1.5 cm.
Slika 5.65: Elementa imata odprti oziroma zaprti prečni prerez
Račun dopustne sile za primer, ko ima element AB odprt prečni prerez
Torzijski vztrajnostni moment nosilca z odprtim tankostenskim prečnim prerezom izračunamo z enačbo
2 r = D − t = 30 − 1.5 = 28.5 cm (glej (2.139))
∫
t 3
I x =
3 dζ = t3 3 L s = 1.53
3 2 π r = 100.727 cm4 .
L s
L s predstavlja integracijsko območje pri integriranju vzdolž srednje črte, L s pa je dolžina srednje črte
tankostenskega prečnega prereza. Silo F 1,dop izračunamo iz pogoja, da je največja strižna napetost
σ xζ,max manjša od dopustne strižne napetosti τ dop
σ xζ,max ≤ τ dop .

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 431
Največjo strižno napetost izračunamo po enačbi (glej enačbo (2.138))
Upoštevamo, da je |M x | max = F 1,dop a in dobimo
σ xζ,max = |M x| max
I x
t max .
Iz zadnje enačbe izračunamo F 1,dop :
F 1,dop a
I x
t max ≤ τ dop .
F 1,dop ≤ τ dop I x 10 · 100.727
= = 13.43 kN.
a t max 50 · 1.5
Račun dopustne sile za primer, ko imat element AB zaprt prečni prerez
Ploščino A s odprtine do srednje črte zaprtega tankostenskega prečnega prereza izračunamo z enačbo
A s = π · 28.52
4
= 637.94 cm 2 .
Silo F 2,dop izračunamo iz pogoja, da je največja strižna napetost σ xζ,max manjša od dopustne strižne
napetosti τ dop
σ xζ,max ≤ τ dop .
Največjo strižno napetost izračunamo po enačbi (glej enačbo (2.150a))
Upoštevamo, da je |M x | max = F 2,dop a in dobimo
σ xζ,max = |M x| max
2 A s t min
.
Iz zadnje enačbe izračunamo F 2,dop :
F 2,dop a
2 A s t min
≤ τ dop .
F 2,dop ≤ τ dop 2 A s t min
a
=
10 · 2 · 637.94 · 1.5
50
= 382.764 kN.
Nosilec z zaprtim tankostenskim prečnim prerezom lahko obtežimo z 28.5-krat večjo silo kot nosilec z
odprtim tankostenskim prečnim prerezom
F 2,dop = 28.50 F 1,dop .
Izpeljemo lahko, da je razmerje med dopustnima silama za odprti in zaprti prečni prerez v obliki kolobarja
enako
F 2,dop
= 3 r
F 1,dop t .

432 5 Uporaba izreka o virtualnih silah
Račun pomika točke C
Pomik w C izračunamo po enačbi
w C = ∑ el
∫ L i
0
(
My δ ¯M y
E I y
+ M x δ ¯M )
x
dx.
G I x
Na sliki 5.66 prikazujemo torzijski moment M x in upogibni moment M y zaradi sile F ter torzijski
moment δ ¯M x in upogibni moment δ ¯M y zaradi virtualne sile δF z = 1.
Slika 5.66: Upogibni in torzijski moment zaradi sile F in virtualne sile δF z = 1
Nosilec z odprtim prečnim prerezom (F 1,dop = 13.43 kN)
Za račun pomika moramo izračunati vztrajnostni moment I y1 prečnega prereza nosilca AB
Tako dobimo
I y1 = π 64 [D4 − (D − 2 t) 4 ] = 13673.73 cm 4 .
w C = 1 F 1,dop L L 2 L
E I y1 2 3 + 1 F 1,dop a a 2 a
E I y2 2 3 + 1 F 1,dop a L a = 0.0507 + 5.0 = 5.0507 cm.
G I x
Delež pomika zaradi upogiba je veliko manjši od deleža zaradi torzije. Nosilci z odprtim tankostenskim
prečnim prerezom slabo prevzamejo torzijsko obtežbo.
Nosilec z zaprtim prečnim prerezom (F 2,dop = 382.764 kN)
Za račun pomika moramo izračunati torzijski vztrajnostni moment I x zaprtega tankostenskega prečnega

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 433
prereza nosilca AB (glej enačbo (2.150b))
I x = ∮
4 A2 s
dζ
t
C s
= 4 · 637.942
π · 28.5
1.5
= 27271.92 cm 4 .
Tako dobimo
w C = F 2,dop
3 E
( ) L
3
+ a3
+ F 2,dop L a 2
= 1.445 + 0.526 = 1.971 cm.
I y1 I y2 G I x
Pomik zaradi torzije je manjši od pomika zaradi upogiba. Nosilci z zaprtim tankostenskim prečnim
prerezom so primerni za prevzem torzijske obtežbe. Kljub temu, da smo konstrukcijo z odprtim prečnim
prerezom obremenili kar z 28.5 krat manjšo silo kot nosilec z zaprtim prerezom, so pomiki pri odprtem
prerezu več kot 2.5 krat večji.
Primer 5.18 Izrazimo ∆T x in ∆T z v enačbi (5.1) za primer nosilca v ravnini x, z! V tem primeru je
sprememba temperature ∆T neodvisna od koordinate y (∆T y = 0). Višino nosilca označimo s h.
Spremembo temperature na spodnji strani nosilca (z = h s ) označimo z ∆T + z , spremembo temperature
na zgornji strani nosilca (z = −h z ) pa z ∆T − z (slika 5.67).
Slika 5.67: Po višini nosilca predpostavimo linearen potek spremembe temperature ∆T
Predpostavimo, da se temperatura linearno spreminja vzdolž koordinate z. To je primerna predpostavka,
če obravnavamo stacionarno stanje, ko se temperatura s časom ne spreminja. Sprememba temperature je
v tem primeru določena z izrazom
∆T = ∆T x + ∆T z z
Izraza za ∆T x in ∆T z dobimo, če upoštevamo robna pogoja na spodnji in zgornji strani nosilca
Ko enačbi rešimo, dobimo
z = h s : ∆T ≡ ∆T + z = ∆T x + ∆T z h s ,
z = −h z : ∆T ≡ ∆T − z = ∆T x − ∆T z h z .
∆T x = ∆T z + − h s(∆T z + − ∆Tz − )
, ∆T z = 1 h
h (∆T z + − ∆Tz − ).

434 5 Uporaba izreka o virtualnih silah
Če sta razdalji h s in h z enaki, sta izraza za določitev ∆T x in ∆T z preprostejša
∆T x = 1 2 (∆T + z + ∆T − z ), ∆T z = 1 h (∆T + z − ∆T − z ). (5.31)
Primer 5.19 Na spodnji strani previsnega linijskega nosilca nastane sprememba temperature ∆T z + =
10 ◦ C, na zgornji strani pa ∆Tz − = 30 ◦ C. Vzemimo, da se ∆T z + in ∆Tz − vzdolž osi nosilca ne
spreminjata. Dolžina nosilca L = 100 cm, višina nosilca h = 10 cm, plošina prečnega prereza
A x = 10 cm 2 , vztrajnostni moment površine prečnega prereza pa I y = 100 cm 4 . Modul elastičnosti
materiala E = 10000 kN/cm 2 , temperaturni razteznostni koeficient pa α T = 10 −5 (1/ ◦ C) (slika 5.68).
Izračunajmo pomika u T in w T ter zasuk ω T ≡ ω T y točke T pri x = L. Določimo tudi potek notranjih
sil!
Slika 5.68: Nosilec v ravnini x, z izpostavimo spremembi temperature ∆T
Konstanti ∆T x in ∆T z izračunamo po enačbi (5.31):
∆T x =
10 + 30
2
= 20 ◦ C, ∆T z =
10 − 30
10
= −2 ◦ C/cm.
Za račun pomikov u T in w T ter zasuka ω T moramo izračunati notranje sile, za virtualni sili δF T x = 1 in
δF T z = 1 in za virtualni moment δM T y = 1 (slika 5.69).
Slika 5.69: Notranje sile zaradi virtualne obtežbe
Ker so notranje sile zaradi resnične obtežbe enake nič, računamo δ ¯W ∗ n po enačbi (glej (5.20))
∫ L
δ ¯W n(∆T ∗ ) = α T (∆T x δ ¯N x + ∆T z δ ¯M y ) dx.
0

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 435
Pri določitvi integralov upoštevamo, da so α T , ∆T x in ∆T z konstante. Zato pomik u T izračunamo tako,
da ploščino diagrama δ ¯N x (δF T x = 1) zaradi virtualne sile δF T x = 1 pomnožimo s konstantama α T in
∆T x ,
u T x = u T = α T ∆T x
∫L
0
δ ¯N x dx = 0.00001 · 20 · 100 · 1 = 0.02 cm.
Vidimo, da ∆T z ne vpliva na pomik u T . Pomik w T izračunamo tako, da ploščino diagrama δ ¯M y (δF T z =
1) zaradi virtualne sile δF T z = 1 pomnožimo s konstantama α T in ∆T z ,
u T z = w T = α T ∆T z
∫L
0
δ ¯M y dx = 0.00001 · (−2) ·
−100 · 100
2
= 0.1 cm.
Vidimo, da na w T ne vpliva sprememba temperature ∆T x ampak samo ∆T z . Zasuk ω T izračunamo
tako, da ploščino diagrama δ ¯M y (δM T y = 1) zaradi virtualnega momenta δM T y = 1 pomnožimo s
konstantama α T in ∆T z
ω T = α T ∆T z
∫L
0
δ ¯M y dx = 0.00001 · (−2) · 100 · 1 = −0.002 rad = −0.115 ◦ .
Iz ravnotežnih pogojev za obravnavani primer sledi, da so notranje sile enake nič. Velja splošno pravilo,
da sprememba temperature v statično določenih konstrukcijah povzroči deformacije ne pa tudi notranjih
sil. Deformirano lego obravnavanega nosilca prikazujemo na sliki 5.70, kjer je merilo pomikov
bistveno večje kot merilo, v katerem je narisana konstrukcija.
Slika 5.70: Statično določeni linijski nosilec se ob spremembi temperature deformira
Primer 5.20 Določimo vodoravni pomik na koncu previsnega nosilca, ki se segreje za
∆T x (x) = 50 + 10 x
[ ◦ C],
kjer moramo razdaljo x podajati v m! Dolžina nosilca je L = 4 m, temperaturni razteznostni koeficient
pa je α T = 1.2 · 10 −5 ( ◦ C) −1 .
Pomik u T na koncu nosilca izračunamo z izrekom o virtualnih silah
u T =
∫ L
0
α T ∆T x δ ¯N x dx.

436 5 Uporaba izreka o virtualnih silah
Diagrama temperaturne spremembe ∆T x in osne sile δ ¯N x zaradi vodoravne virtualne sile δF x = 1 v
točki T prikazujemo na sliki 5.71.
Slika 5.71: Diagrama ∆T x in δ ¯N x
Sedaj lahko zapišemo enačbo za račun vodoravnega pomika
u T = α T
50 + 90
2
L · 1 = 1.2 · 10 −5 ·
50 + 90
2
· 4 = 0.0034 m = 0.34 cm.
5.1.6 Delo virtualnih napetosti v linearno elastičnih vzmeteh
Določimo delo δW ∗ n virtualnih napetosti na resničnih deformacijah za ravni linijski nosilec s konstantnim
prečnim prerezom A x in dolžino L, ki je v krajišču A obtežen s silo F Ax , v krajišču B pa s silo F Bx ! Sili
F Ax in F Bx sta enako veliki in nasproti usmerjeni (slika 5.72). Delo δW ∗ n izrazimo s pomikoma u Ax in
u Bx krajišč nosilca.
Slika 5.72: Nosilec je obtežen v krajiščih s silama F Ax in F Bx
Da bi δW ∗ n izrazili s pomikoma krajišč nosilca u Ax in u Bx postavimo v krajna prereza virtualni sili δF Ax
in δF Bx , ki sta enaki po velikosti in nasproti usmerjeni (slika 5.73).
Slika 5.73: Nosilec je obtežen v krajišču A s silo δF Ax , v krajišču B pa s silo δF Bx

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 437
Delo virtualnih napetosti na resničnih deformacijah izrazimo s pomikoma u Ax in u Bx , če za obravnavani
primer v izreku o virtualnih silah δW ∗ z izrazimo s silama δF Ax in δF Bx
Ker je osna sila δN x zaradi virtualne obtežbe enaka
sledi
δW ∗ n = δW ∗ z = δF Bx u Bx − δF Ax u Ax .
δN x = δF Ax = δF Bx ,
δW ∗ n = δN x (u Bx − u Ax ).
Prikazani element lahko predstavlja linijsko vzmet, ki jo shematično narišemo na sliki 5.74.
Slika 5.74: Linijska vzmet
Če vpeljemo oznaki
dobimo
δN x ≡ δN v , ∆u v ≡ u Bx − u Ax ,
δW ∗ n = δN v ∆u v .
Pri tem je δN v notranja sila v vzmeti zaradi virtualne obtežbe, ∆u v pa sprememba dolžine vzmeti zaradi
resnične obtežbe.
Določimo delo δW ∗ n virtualnih napetosti na resničnih deformacijah za ravni linijski nosilec s konstantnim
prečnim prerezom A x in dolžino L, ki je v krajišču A obtežen s torzijskim momentom M Ax , v krajišču
B pa s torzijskim momentom M Bx . Torzijska momenta M Ax in M Bx sta enako velika in nasproti
usmerjena (slika 5.75). Delo δW ∗ n izrazimo s torzijskima zasukoma ω Ax in ω Bx krajišč nosilca.
Slika 5.75: Nosilec je obtežen v krajiščih s torzijskima momentoma M Ax in M Bx
Da bi δW ∗ n izrazili z zasukoma krajnih prerezov nosilca ω Ax in ω Bx , postavimo v krajna prereza virtualna
torzijska momenta δM AX in δM BX , ki sta enaka po velikosti in nasproti usmerjena (slika 5.76).

438 5 Uporaba izreka o virtualnih silah
Slika 5.76: Nosilec je obtežen v krajišču A z virtualnim torzijskim momentom δM Ax , v krajišču
B pa z virtualnim torzijskim momentom δM Bx
Delo δW ∗ n določimo tako, da v izreku o virtualnih silah δW ∗ z izrazimo z momentoma δM Ax in δM Bx
δW ∗ n = δW ∗ z = δM Bx ω Bx − δM Ax ω Ax .
Ker je notranji torzijski moment δM x zaradi virtualne obtežbe enak δM Ax oziroma δM Bx
sledi
δM x = δM Ax = δM Bx ,
δW ∗ n = δM x (ω Bx − ω Ax ).
Prikazani element lahko predstavlja torzijsko vzmet. Prečno povezavo dveh linijskih nosilcev s torzijsko
vzmetjo prikazujemo na sliki 5.77.
Slika 5.77: Torzijska vzmet: a) v ravnini
b) v prostoru
Z oznakama
dobimo
δM x ≡ δM v , ∆ω v ≡ ω Bx − ω Ax ,
δW ∗ n = δM v ∆ω v .
Z δM v označujemo notranji torzijski moment v vzmeti zaradi virtualne obtežbe, ∆ω v pa predstavlja
spremembo zasuka torzijske vzmeti zaradi resnične obtežbe.
V primeru, da je v konstrukciji n v osnih in m v torzijskih vzmeti, je delo virtualnih napetosti na resničnih
deformacijah v vseh vzmeteh enako
∑n v
∑m v
δWn ∗ = δN vi ∆u vi + δM vj ∆ω vj .
i=1
Če so vzmeti linearno elastične, lahko izrazimo notranjo silo N vi oziroma notranji moment M vj vzmeti
s togostnima koeficientoma k vi in k ϕj (slika 5.78)
j=1
N vi = k vi ∆u vi , M vj = k ϕj ∆ω vj ,

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 439
kjer togost vzmeti lahko izrazimo z enačbama
k vi = E i A xi
L i
, k ϕj = G j I xj
L j
.
Slika 5.78: Linearno elastični vzmeti
V tem primeru je delo δW ∗ n v vseh vzmeteh enako
δW ∗ n =
∑n v
i=1
N vi
∑m v
M vj
δN vi + δM vj . (5.32)
k vi k
j=1 ϕj
Delo δW ∗ n virtualnih napetosti na resničnih deformacijah za konstrukcijo sestavljeno iz linijskih elementov
in vzmeti dobimo, če seštejemo enačbe (5.11) in (5.32):
δW ∗ n = ∑ el
+
∫ L i
0
(
My
∑n v
+
i=1
(( )
Nx
+ α T ∆T x δN x + N y δN y
E A x GA y
E I y
+ α T ∆T z
)
δM y +
N vi
∑m v
M vj
δN vi + δM vj .
k vi k
j=1 ϕj
+ N z δN z
GA z
(
Mz
E I z
− α T ∆T y
)
δM z
)
dx+
+ M x δM x
G I x
+
(5.33)
Če ima virtualna sila oziroma virtualni moment velikost ena, potem količine δW ∗ n, δN x , δN y , δN z , δM x ,
δM y , δM z , δN vi in δM vj označimo s prečko in dobimo:
}
u T s
= δ
ω ¯W n ∗ = ∑
T s
el
+
∫ L i
0
(
My
∑n v
+
i=1
(( )
Nx
+ α T ∆T x δ
E A ¯N x + N y δ ¯N y
x G A y
E I y
+ α T ∆T z
)
δ ¯M y +
N vi
δ
k ¯N
∑m v
M vj
vi + δ
vi k ¯M vj .
j=1 ϕj
+ N z δ ¯N z
G A z
(
Mz
E I z
− α T ∆T y
)
δ ¯M z
)
dx+
+ M x δ ¯M x
G I x
+
(5.34)

440 5 Uporaba izreka o virtualnih silah
Slika 5.79: Konzola je vpeta s torzijsko linearno elastično vzmetjo
Primer 5.21 Za nosilec na sliki 5.79 določimo navpični pomik w T točke T zaradi sile F T z ! Vzmet je
linearno elastična. Vpliv prečne sile N z zanemarimo.
Če prečno silo N z zanemarimo, izračunamo pomik w T po enačbi
w T = δ ¯W ∗ n (δF T z = 1.0) =
∫ L
0
M y δ ¯M y
E I y
dx + M v
k ϕ
δ ¯M v .
Upogibni moment v nosilcu in v vzmeti zaradi resnične obtežbe prikazujemo na sliki 5.80
M v = −F T z L.
Slika 5.80: Upogibni moment zaradi sile F T z
Upogibni moment v nosilcu in v vzmeti zaradi virtualne sile δF T z v točki T prikazujemo na sliki 5.81
δ ¯M v = −L.
Slika 5.81: Upogibni moment zaradi virtualne sile δF T z = 1
Navpični pomik točke T je
w T = 1 F T z L L 2
E I y 2 3 L + F T z L
L = F T z L 3
+ F T z L 2
.
k ϕ 3 E I y k ϕ

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 441
Pomik osi nosilca je sestavljen iz pomika zaradi upogiba nosilca in iz pomika zaradi zasuka elastične
podpore. Na sliki 5.82 prikazujemo pomik nosilca zaradi zasuka elastične podpore in zaradi upogiba
nosilca. Izpeljani izrazi veljajo le za majhne pomike, zato moramo povdariti, da je merilo pomikov
zaradi preglednosti povečano.
Slika 5.82: Navpični pomik nosilca
Primer 5.22 Določimo navpični pomik točke T . Vzmeti sta linearno elastični (slika 5.83).
Slika 5.83: Konstrukcija je sestavljena iz dveh nosilcev in dveh vzmeti
Pomik določimo z izrekom o virtualnih silah po enačbi (5.34), kjer upoštevamo, da sta od nič različna
le prečna sila in upogibni moment v nosilcu in sila oziroma moment v vzmeteh. Ker vpliv prečne sile
zanemarimo, je:
w T =
∫ 2a
0
M y δ ¯M y
dx + N v δ ¯N v
+ M v δ ¯M v
.
EI y k x k ϕ
Notranje sile zaradi zunanje obtežbe prikazujemo na sliki 5.84.
Slika 5.84: Diagram upogibnega momenta zaradi zunanje obtežbe

442 5 Uporaba izreka o virtualnih silah
Osna sila in upogibni moment v vzmeteh sta: N v = −F/2 in M v = P a/2.
Notranje sile zaradi virtualne obtežbe δF z = 1 prikazujemo na sliki 5.85.
Slika 5.85: Diagram upogibnega momenta zaradi virtualne sile
Osna sila in upogibni moment v vzmeteh zaradi virtualne sile sta: δ ¯N v = −1/2 in δ ¯M v = a/2.
Navpični pomik točke T je
in po preureditvi enačbe dobimo
w T = 1 F a a
E I y 2 2
w T = F
2
3
a
2 2 + F/2 1
k x
2 + F a/2
k ϕ
( a
3
6 E I y
+ 1
4 k x
+ a2
4 k ϕ
)
.
Primer 5.23 Določimo število navojev n gosto navite vzmeti na sliki 5.86 tako, da bo navpični pomik
w T točke T enak 1 cm.
a
2
Slika 5.86: Prostoležeči nosilec je v enem krajišču podprt z gosto navito vzmetjo
Spremembo dolžine ∆u v gosto navite vzmeti, ki je osno obtežena z natezno ali tlačno silo F , izračunamo
po enačbi (glej primer 5.29)
∆u v = 4 ¯r3 n N v
G r 4 , (5.35)

5.1 Pomiki in zasuki posameznih točk statično določenih linijskih konstrukcij 443
kjer je ¯r polmer vzmeti, r polmer žice vzmeti, G strižni modul jekla, N v pa osna sila v vzmeti.
Dolžina nosilca je L = 1.0 m, modul elastičnosti nosilca je E n = 20000 kN/cm 2 , vztrajnostni moment
nosilca je I n = 54 cm 4 , obtežba pa je M = 2 kNm. Polmer vzmeti ¯r = 5.0 cm, polmer žice vzmeti
r = 0.771 cm, strižni modul jekla G je 8000 kN/cm 2 .
Ker je togost razmerje med silo v vzmeti in spremembo dolžine (k v = N v /∆u v ), sledi iz enačbe (5.35),
da je togost enaka
Pomik izračunamo po enačbi (5.34)
w T =
∫ L
0
k v = G r4
4 ¯r 3 n .
M y δ ¯M y
E I y
dx + N v δ ¯N v
k v
.
Diagrama notranjih sil zaradi zunanje obtežbe in zaradi obtežbe z virtualno silo δF z = 1 prikazujemo na
sliki 5.87.
Slika 5.87: Upogibni moment zaradi zunanje obtežbe M in zaradi δF z = 1
Osna sila N v v vzmeti zaradi obtežbe M je −M/L, zaradi virtualne obtežbe pa δN v = −0.5. Pomik w T
je
w T = 1 L L 1 M
E n I n 4 2 2 + M 4 ¯r 3 n
2 L G r 4 = M L2
+ 2 M ¯r3 n
16 E n I n G L r 4 .
Število potrebnih navojev n je
n =
(w T − M ) (
) L2 G L r
4
16 E n I n 2 M ¯r 3 = 200 · 1002 8000 · 100 · 0.771
4
1 −
16 · 20000 · 54 2 · 200 · 5 3 = 5.

444 5 Uporaba izreka o virtualnih silah
Primer 5.24 Podan je pomik w A podpore A na sliki 5.88. Izračunajmo pomik w 1 na mestu delovanja
sile F 1 !
Slika 5.88: Poleg obtežbe s silama upoštevamo še pomik podpore
Konstrukcija je statično določena. Pomik podpore nima vpliva na notranje sile statično določene konstrukcije,
vpliva pa na pomike take konstrukcije. Pomik v določeni točki določimo z izrekom o virtualnih
silah
δW ∗ z = δW ∗ n.
Konstrukcijo v prijemališču sile F 1 obtežimo z virtualno silo δF z = 1 (slika 5.89).
Slika 5.89: Virtualna obtežba δF z = 1 ter ustrezne reakcije
Ker ima podpora predpisan pomik v navpični smeri, opravi delo δW ∗ z tudi reakcija δA z , ki jo izrazimo z
virtualno silo δF z = 1 takole:
Delo δW ∗ z zapišemo z enačbo
delo δW ∗ n pa zapišemo v tem primeru takole:
δA z a + δF z
a
2 = 0 → δA z = − δF z
2 = −1 2 .
δW ∗ z = δA z w A + δF z w 1 = − 1 2 w A + w 1 ,
δW ∗ n = ∑ el
∫ L
0
M y δ ¯M y
E I y
dx +
2∑
i=1
N vi
k vi
δ ¯N vi .