1.3 Strizni in precni normalni napetosti v nosilcu s konstantnim ...
1.3 Strizni in precni normalni napetosti v nosilcu s konstantnim ...
1.3 Strizni in precni normalni napetosti v nosilcu s konstantnim ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
1.2 Pomiki <strong>in</strong> vzdolžna normalna napetost 115<br />
Tabela 1.14: Koord<strong>in</strong>ate konveksnih točk v smeri η <strong>in</strong> ζ <strong>in</strong> odseki η o <strong>in</strong> ζ o<br />
Točka na vogalu y z η ζ η o ζ o<br />
1 −6.79 −4.21 −4.32 −6.72 0.89 3.02<br />
2 2.21 −4.21 3.81 −2.86 −1.01 7.09<br />
3 2.21 8.79 −1.77 8.89 2.17 −2.28<br />
4 1.21 8.79 −2.67 8.46 1.43 −2.40<br />
5 −6.79 −3.21 −4.75 −5.81 0.81 3.48<br />
Koord<strong>in</strong>ate mejnih točk jedra prereza izračunamo po enačbah<br />
η P =<br />
(ζ Na − ζ Nb ) i 2 ζ<br />
η Na ζ Nb − ζ Na η Nb<br />
, ζ P = (η Nb − η Na ) i 2 η<br />
η Na ζ Nb − ζ Na η Nb<br />
,<br />
i 2 η = I η<br />
= 425.55 = 20.26 cm 2 , i 2 ζ<br />
A x 21<br />
= I ζ<br />
= 80.53 = 3.83 cm 2 ,<br />
A x 21<br />
zapišemo v preglednici 1.15 <strong>in</strong> prikazujemo na sliki 1.89.<br />
Tabela 1.15: Račun koord<strong>in</strong>at točk, ki določajo jedro prereza<br />
Prijemališče η Na ζ Na ζ Na − ζ Nb η Na ζ Nb − ζ Na η Nb η P Točka<br />
sile N η Nb ζ Nb η Nb − η Na ζ P jedra<br />
1 −4.32 −6.72 −3.86 37.93 −0.39 A<br />
2 3.81 −2.86 8.13 4.34<br />
2 3.81 −2.86 −11.74 28.79 −1.56 B<br />
3 −1.77 8.89 −5.58 −3.93<br />
3 −1.77 8.89 0.43 8.79 0.19 C<br />
4 −2.67 8.46 −0.90 −2.08<br />
4 −2.67 8.46 14.27 55.71 0.98 D<br />
5 −4.75 −5.81 −2.08 −0.76<br />
5 −4.75 −5.81 0.90 6.79 0.51 E<br />
1 −4.32 −6.72 0.43 1.28<br />
Primer izračunajmo še za osi y, z, ki nista glavni vztrajnostni osi. Normalno napetost σ xx izračunamo<br />
z enačbo (1.88)<br />
σ xx = N x<br />
− M z I yz − M y I z<br />
A x I y I z − Iyz<br />
2 z − M z I y − M y I yz<br />
I y I z − Iyz<br />
2 y.<br />
Enačba nevtralne osi je<br />
σ xx = 0 = N x<br />
− M z I yz − M y I z<br />
A x I y I z − Iyz<br />
2<br />
z − M z I y − M y I yz<br />
I y I z − Iyz<br />
2 y.
116 1 Upogib z osno silo<br />
Slika 1.89: Jedro prereza kotnega prečnega prereza<br />
Upoštevamo oznake<br />
<strong>in</strong> dobimo<br />
Odseka y o <strong>in</strong> z o sta:<br />
(<br />
N<br />
A x<br />
N x = N, M y = N z N , M z = −N y N<br />
1 + y N I yz + z N I z<br />
I y I z − Iyz<br />
2<br />
A x z + y )<br />
N I y + z N I yz<br />
I y I z − Iyz<br />
2 A x y = 0. (1.167)<br />
(<br />
)<br />
( )<br />
y o = − 1 Iy I z − Iyz<br />
2 , z o = − 1 Iy I z − Iyz<br />
2 .<br />
A x y N I y + z N I yz A x y N I yz + z N I z<br />
Enačbo (1.167) zapišimo za primera, da je sila N v točki s koord<strong>in</strong>atama y Na , z Na <strong>in</strong> v točki y Nb , z Nb .<br />
S tem dobimo enačbi za premici a <strong>in</strong> b:<br />
Konstante A 1 , A 2 , B 1 <strong>in</strong> B 2 so<br />
premica a : A 1 y + A 2 z + 1 = 0,<br />
premica b : B 1 y + B 2 z + 1 = 0.<br />
A 1 = y Na I y + z Na I yz<br />
I y I z − Iyz<br />
2 A x ,<br />
B 1 = y Nb I y + z Nb I yz<br />
I y I z − Iyz<br />
2 A x ,<br />
A 2 = y Na I yz + z Na I z<br />
I y I z − Iyz<br />
2 A x ,<br />
B 2 = y Nb I yz + z Nb I z<br />
I y I z − Iyz<br />
2 A x .
1.2 Pomiki <strong>in</strong> vzdolžna normalna napetost 117<br />
Koord<strong>in</strong>ati presečišča premic a <strong>in</strong> b izračunamo z enačbama:<br />
y p =<br />
A 2 − B 2<br />
A 1 B 1 − A 2 B 1<br />
, z p =<br />
B 1 − A 1<br />
A 1 B 1 − A 2 B 1<br />
.<br />
Tabela 1.16: Presečišča premic, ki določajo jedro prereza, z osema y <strong>in</strong> z<br />
Točka robu prereza y N z N y o = −i 2 z/y N z o = −i 2 y/z N<br />
1 −6.79 −4.21 0.86 −5.43<br />
2 2.21 −4.21 −1.20 1.81<br />
3 2.21 8.79 4.37 −1.68<br />
4 1.21 8.79 2.22 −1.48<br />
5 −6.79 −3.21 0.81 −3.67<br />
V preglednici 1.17 zapišemo račun koord<strong>in</strong>at točk na robu jedra prereza za prečni prerez oblike črke T.<br />
Tabela 1.17: Račun koord<strong>in</strong>at točk, ki določajo jedro prereza<br />
Prijemališče y Na z Na A 1 A 2 y P Točka<br />
sile N y Nb z Nb B 1 B 2 z P jedra<br />
1 −6.79 −4.21 −1.160 0.184 1.51 A<br />
2 2.21 −4.21 0.837 −0.554 4.09<br />
2 2.21 −4.21 0.837 −0.554 −3.10 B<br />
3 2.21 8.79 −0.229 0.594 −2.88<br />
3 2.21 8.79 −0.229 0.594 −0.72 C<br />
4 1.21 8.79 −0.451 0.676 −1.96<br />
4 1.21 8.79 −0.451 0.676 0.56 D<br />
5 −6.79 −3.21 −1.242 0.272 −1.10<br />
5 −6.79 −3.21 −1.242 0.272 1.01 E<br />
1 −6.79 −4.21 −1.160 0.184 0.94
118 1 Upogib z osno silo<br />
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim<br />
prerezom<br />
Pri upogibu ravnega nosilca s <strong>konstantnim</strong> prečnim prerezom A x upoštevamo razen vzdolžne normalne<br />
<strong>napetosti</strong> σ xx tudi strižni <strong>napetosti</strong> σ xy <strong>in</strong> σ xz (slika 1.90).<br />
Slika 1.90: V <strong>nosilcu</strong> upoštevamo vzdolžno normalno napetost σ xx ter strižni <strong>napetosti</strong> σ xy <strong>in</strong> σ xz<br />
Pri izpeljavi enačb za račun pomikov u, v <strong>in</strong> w (enačbe (1.80) <strong>in</strong> (1.87)) ter enačbe za vzdolžno normalno<br />
napetost σ xx (enačba (1.88)) v <strong>nosilcu</strong> z ravno osjo smo predpostavili, da sta od nič različni le vzdolžna<br />
normalna deformacija ε xx <strong>in</strong> le vzdolžna normalna napetost σ xx . Enačbe za σ xy , σ xz , σ yy <strong>in</strong> σ zz izpeljemo<br />
iz ravnotežnih enačb za ustrezni del nosilca.<br />
Vzemimo del nosilca od ¯x = 0 do ¯x = x ter ga odrežimo pri y = y ∗ = konst (slika 1.91).<br />
Slika 1.91: Obravnavamo del nosilca dolž<strong>in</strong>e x z delnim prečnim prerezom A ∗<br />
x
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 119<br />
Zapišimo ravnotežno enačbo za ta nosilec:<br />
∫<br />
A ∗<br />
x (0)<br />
+<br />
∫ x<br />
0<br />
⃗p S (0, y, z) dA x +<br />
⎛<br />
⎜<br />
⎝<br />
C ∗<br />
∫<br />
∫<br />
A ∗<br />
x (x)<br />
x,z (¯x) ⃗p S (¯x, c) dc +<br />
∫<br />
A ∗<br />
⃗σ x (x, y, z) dA x +<br />
x (¯x) ⃗v(¯x, y, z) dA x +<br />
⎞<br />
∫<br />
⃗σ y (¯x, y ∗ , z) dc⎟<br />
⎠ d¯x = ⃗0.<br />
x,01 (¯x)<br />
C ∗<br />
(1.168)<br />
S c označimo krivuljsko koord<strong>in</strong>ato, ki določa točke mejne črte dela prečnega prereza Ax ∗ . Del v oglatem<br />
∗<br />
oklepaju označimo z F ⃗ (x) <strong>in</strong> predstavlja nadomestno l<strong>in</strong>ijsko obtežbo zaradi zunanje obtežbe ⃗pS na<br />
mejni črti C ∗ x,z ter zunanje obtežbe ⃗v na delu prereza Ax ∗ <strong>in</strong> zaradi <strong>napetosti</strong> ⃗σ y vzdolž meje C ∗ x,01<br />
∫<br />
∫<br />
∫<br />
∫<br />
⃗F ∗ ∗<br />
(x) = ⃗p S dc + ⃗v dA x + ⃗σ y dc = P ⃗ (x) + ⃗σ y dc. (1.169)<br />
C ∗<br />
x,z(x)<br />
A ∗<br />
x (x)<br />
C ∗<br />
x,01(x)<br />
C ∗<br />
x,01(x)<br />
∗<br />
S P ⃗ (x) označimo zunanjo l<strong>in</strong>ijsko obtežbo za del prereza A ∗<br />
x<br />
∫<br />
∫<br />
⃗P ∗ (x) = ⃗p S dc + ⃗v dA x . (1.170)<br />
C ∗<br />
x,z (x) A ∗<br />
x (x)<br />
Enačbo (1.168) krajše zapišemo takole:<br />
∫<br />
A ∗<br />
x (0) ⃗p S dA x +<br />
∫<br />
A ∗<br />
x (x) ⃗σ x dA x +<br />
∫ x<br />
0<br />
⃗F ∗ (¯x) d¯x = ⃗0. (1.171)<br />
Ax ∗ (x) ne predstavlja funkcijske zveze temveč le označuje za kateri prečni prerez gre. Ker v nadaljevanju<br />
obravnavamo le prečni prerez pri x <strong>in</strong> sta njegova oblika <strong>in</strong> velikost neodvisni od x, <strong>in</strong>tegracijsko območje<br />
krajše zapišemo z Ax ∗ , Cx,01 ∗ <strong>in</strong> C x,z. ∗ Enačba (1.171) predstavlja ravnotežno enačbo za del nosilca. Če<br />
želimo določiti <strong>napetosti</strong> v odvisnosti od x, moramo enačbo (1.171) odvajati. Tedaj dobimo:<br />
∫<br />
∂<br />
∂x<br />
A ∗<br />
x<br />
∫<br />
∗<br />
⃗σ x dA x + F ⃗<br />
∂ =<br />
∂x<br />
A ∗<br />
x<br />
⃗σ x dA x + ⃗ P<br />
∗<br />
+<br />
∫<br />
C ∗<br />
x,01<br />
⃗σ y dc = ⃗0 (1.172)<br />
oziroma<br />
∫<br />
∂<br />
∂x<br />
A ∗<br />
x<br />
∫h ∗<br />
∗<br />
⃗σ x dA x + P ⃗ + ⃗σ y dc = ⃗0. (1.173)<br />
0
120 1 Upogib z osno silo<br />
Predpostavimo tudi, da se ⃗σ y vzdolž meje Cx,01 ∗ ne sprem<strong>in</strong>ja. Ker je A ∗<br />
x<br />
določimo tako, da odvajamo <strong>in</strong>tegrand (glej Bronste<strong>in</strong> ... str 341)<br />
∫<br />
A ∗<br />
x<br />
konstanten, odvod <strong>in</strong>tegrala<br />
∂⃗σ x<br />
∂x dA x + ⃗ P<br />
∗<br />
+ ⃗σy h ∗ = ⃗0. (1.174)<br />
Iz enačbe (1.174) izrazimo ⃗σ y<br />
⃗σ y = − 1 h ∗ ⎛<br />
⎜<br />
⎝ ⃗ P ∗ +<br />
∫<br />
A ∗<br />
x<br />
⎞<br />
∂⃗σ x<br />
∂x dA ⎟<br />
x⎠ . (1.175)<br />
Po množenju (1.175) z enotskim vektorjem ⃗e x , dobimo izraz za strižno napetost σ yx<br />
⎛<br />
σ yx = σ xy = − 1 ∫<br />
⎜<br />
h ∗ ⎝Px ∗ +<br />
A ∗<br />
x<br />
∂σ xx<br />
⎞<br />
∂x dA ⎟<br />
x⎠ , (1.176)<br />
po množenju (1.175) z enotskim vektorjem ⃗e y pa izraz za prečno normalno napetost σ yy<br />
σ yy = − 1 h ∗ ⎛<br />
⎜<br />
⎝P ∗<br />
y +<br />
∫<br />
A ∗<br />
x<br />
∂σ xy<br />
⎞<br />
∂x dA ⎟<br />
x⎠ . (1.177)<br />
Pri izpeljavi enačb (1.176) <strong>in</strong> (1.177) smo predpostavili, da sta strižna napetost σ xy ter prečna normalna<br />
napetost σ yy vzdolž črte, ki je vzporedna osi z, konstantni (glej enačbi (1.173) <strong>in</strong> (1.174)).<br />
Izpeljava enačb za račun strižne <strong>napetosti</strong> σ xz <strong>in</strong> prečne normalne <strong>napetosti</strong> σ zz<br />
Vzemimo del nosilca od ¯x = 0 do ¯x = x ter ga odrežimo pri z = z ∗ = konst (slika 1.92).<br />
Zapišimo ravnotežno enačbo za ta nosilec:<br />
∫<br />
A ∗<br />
⃗p S (0, y, z) dA x + ⃗σ x (x, y, z) dA x +<br />
x (0) A ∗<br />
x<br />
⎛<br />
(x)<br />
∫ x ∫<br />
∫<br />
+ ⎜<br />
⎝ ⃗p S (¯x, c) dc + ⃗v(¯x, y, z) dA x +<br />
0 C ∗<br />
x,z (¯x) A ∗<br />
x (¯x)<br />
∫<br />
⎞<br />
∫<br />
⃗σ z (¯x, y, z ∗ ) dc⎟<br />
⎠ d¯x = ⃗0.<br />
x,01 (¯x)<br />
C ∗<br />
(1.178)
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 121<br />
Slika 1.92: Obravnavamo del nosilca dolž<strong>in</strong>e x z delnim prečnim prerezom A ∗<br />
x<br />
∗<br />
Del v oglatem oklepaju označimo z F ⃗ (x) <strong>in</strong> predstavlja nadomestno l<strong>in</strong>ijsko obtežbo zaradi zunanje<br />
obtežbe na mejni črti Cx,z ∗ ter na delu prereza Ax ∗ <strong>in</strong> zaradi <strong>napetosti</strong> ⃗σ z vzdolž meje Cx,01<br />
∗<br />
∫<br />
∫<br />
∫<br />
∫<br />
⃗F ∗ ∗<br />
(x) = ⃗p S dc + ⃗v dA x + ⃗σ z dc = P ⃗ (x) + ⃗σ z dc. (1.179)<br />
C ∗<br />
x,z (x) A ∗<br />
x (x) C ∗<br />
x,01 (x) C ∗<br />
x,01 (x)<br />
∗<br />
S P ⃗ (x) označimo zunanjo l<strong>in</strong>ijsko obtežbo za del prereza A ∗<br />
x<br />
∫<br />
∫<br />
⃗P ∗ (x) = ⃗p S dc + ⃗v dA x . (1.180)<br />
Enačbo (1.178) krajše zapišemo takole:<br />
∫<br />
A ∗<br />
x (0)<br />
⃗p S dA x +<br />
C ∗<br />
x,z(x)<br />
∫<br />
A ∗<br />
x (x)<br />
A ∗<br />
x (x)<br />
∫ x<br />
⃗σ x dA x +<br />
0<br />
⃗F ∗ (¯x) d¯x = ⃗0. (1.181)<br />
Z odvajanjem ravnotežne enačbe (1.181) po x dobimo (namesto Ax ∗ (x) pišemo Ax ∗ )<br />
∫<br />
∫<br />
∫<br />
∂<br />
∗<br />
⃗σ x dA x + F ⃗<br />
∂<br />
∗<br />
= ⃗σ x dA x + P ⃗ + ⃗σ z dc = ⃗0 (1.182)<br />
∂x<br />
∂x<br />
oziroma<br />
A ∗<br />
x<br />
∫<br />
∂<br />
∂x<br />
A ∗<br />
x<br />
A ∗<br />
x<br />
C ∗<br />
x,01<br />
∫b ∗<br />
∗<br />
⃗σ x dA x + P ⃗ + ⃗σ z dc = ⃗0. (1.183)<br />
0
122 1 Upogib z osno silo<br />
Upoštevamo, da je Ax ∗ konstanten ter predpostavimo, da se ⃗σ z vzdolž Cx,01 ∗ ne sprem<strong>in</strong>ja<br />
∫<br />
∂⃗σ x<br />
∂x dA ∗<br />
x + P ⃗ + ⃗σz b ∗ = ⃗0. (1.184)<br />
A ∗<br />
x<br />
Iz enačbe (1.184) izrazimo ⃗σ z<br />
⃗σ z = − 1 b ∗ ⎛<br />
⎜<br />
⎝ ⃗ P ∗ +<br />
∫<br />
A ∗<br />
x<br />
⎞<br />
∂⃗σ x<br />
∂x dA ⎟<br />
x⎠ . (1.185)<br />
Po množenju (1.185) z enotskim vektorjem ⃗e x , dobimo izraz za strižno napetost σ zx<br />
⎛<br />
⎞<br />
σ zx = σ xz = − 1 ∫<br />
⎜<br />
b ∗ ⎝Px ∗ ∂σ xx<br />
+<br />
∂x dA ⎟<br />
x⎠ , (1.186)<br />
po množenju (1.185) z enotskim vektorjem ⃗e z pa izraz za prečno normalno napetost σ zz<br />
⎛<br />
⎞<br />
σ zz = − 1 ∫<br />
⎜<br />
b ∗ ⎝Pz ∗ ∂σ xz<br />
+<br />
∂x dA ⎟<br />
x⎠ . (1.187)<br />
Pri izpeljavi enačb (1.186) <strong>in</strong> (1.187) smo predpostavili, da sta strižna napetost σ xz ter prečna normalna<br />
napetost σ zz vzdolž črte, ki je vzporedna osi y, konstantni (glej enačbi (1.183) <strong>in</strong> (1.184)).<br />
V izrazih za strižni <strong>napetosti</strong> σ xy <strong>in</strong> σ xz nastopa <strong>in</strong>tegral na delu A ∗<br />
x odvoda vzdolžne normalne <strong>napetosti</strong><br />
σ xx po x. Če vzamemo, da sta osi y <strong>in</strong> z glavni vztrajnostni osi v težišču prečnega prereza A x , je<br />
napetost σ xx povezana z osno silo N x <strong>in</strong> upogibnima momentoma M y <strong>in</strong> M z po enačbi (1.89)<br />
A ∗<br />
x<br />
A ∗<br />
x<br />
σ xx = N x<br />
+ M y<br />
z − M z<br />
y. (1.188)<br />
A x I y I z<br />
Integral odvoda normalne <strong>napetosti</strong> σ xx je<br />
∫<br />
∫<br />
∂σ xx<br />
∂x dA x =<br />
A ∗<br />
x<br />
=<br />
A ∗<br />
x<br />
∫<br />
A ∗<br />
x<br />
∂<br />
∂x<br />
(<br />
Nx<br />
+ M y<br />
z − M )<br />
z<br />
y dA x =<br />
A x I y I z<br />
( 1<br />
A x<br />
dN x<br />
dx + 1 I y<br />
dM y<br />
dx z − 1 I z<br />
dM z<br />
dx y )<br />
dA x =<br />
= − A∗ x<br />
P x + N z − M y<br />
Sy ∗ + N y + M z<br />
Sz ∗ .<br />
A x I y<br />
I z<br />
(1.189)
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 123<br />
Uporabili smo oznake<br />
A ∗ x =<br />
∫<br />
dA x , S ∗ y =<br />
∫<br />
z dA x , S ∗ z =<br />
∫<br />
y dA x , (1.190)<br />
A ∗<br />
x<br />
A ∗<br />
x<br />
A ∗<br />
x<br />
ter upoštevali ravnotežne enačbe za ravni l<strong>in</strong>ijski nosilec (enačbe (<strong>1.3</strong>0) <strong>in</strong> (<strong>1.3</strong>1))<br />
dN x<br />
dx = −P x,<br />
dM y<br />
dx = N z − M y ,<br />
dM z<br />
dx = −N y − M z . (1.191)<br />
Enačbo (1.189) vstavimo v enačbo (1.176) <strong>in</strong> dobimo izraz za strižno napetost σ xy<br />
σ xy = − 1 h ∗ (<br />
)<br />
Px ∗ − A∗ x<br />
P x + S∗ y<br />
(N z − M y ) + S∗ z<br />
(N y + M z ) . (1.192)<br />
A x I y I z<br />
Če (1.189) vstavimo v enačbo (1.186), dobimo izraz za strižno napetost σ xz<br />
σ xz = − 1 b ∗ (<br />
)<br />
Px ∗ − A∗ x<br />
P x + S∗ y<br />
(N z − M y ) + S∗ z<br />
(N y + M z ) . (1.193)<br />
A x I y I z<br />
Pri izpeljavi enačbe (1.192) predpostavimo, da je strižna napetost σ xy vzdolž črte, ki je vzporedna glavni<br />
vztrajnostni osi z, konstantna (slika 1.93a). Pri izpeljavi enačbe (1.193) privzamemo, da se strižna<br />
napetost σ xz vzdolž črte, ki je vzporedna glavni vztrajnostni osi y, ne sprem<strong>in</strong>ja (slika 1.93b).<br />
Slika 1.93: a) Del prereza Ax ∗ za račun <strong>napetosti</strong> σ xy b) Del prereza Ax<br />
∗ za račun <strong>napetosti</strong><br />
σ xz<br />
Velikosti prečnih <strong>normalni</strong>h <strong>napetosti</strong> σ yy <strong>in</strong> σ zz so pri nosilcih majhne v primerjavi z velikostmi <strong>napetosti</strong><br />
σ xx , σ xy <strong>in</strong> σ xz <strong>in</strong> jih zato običajno ne računamo (glej primer <strong>1.3</strong>1).<br />
V primeru upogiba z osno silo se nosilec ne zasuče okrog vzdolžne osi x. Točko S, skozi katero morata<br />
potekati smernici rezultant strižnih <strong>napetosti</strong> σ xy <strong>in</strong> σ xz (prečnih sil N y <strong>in</strong> N z ) v prečnem prerezu A x ,<br />
da se prerez ne zasuče, imenujemo strižno središče (slika 1.94).
124 1 Upogib z osno silo<br />
Slika 1.94: a) Strižni <strong>napetosti</strong> σ xy <strong>in</strong> σ xz v prečnem prerezu A x<br />
b) Prečni sili N y <strong>in</strong> N z v strižnem središču prečnega<br />
prereza A x<br />
Če prečni sili N y <strong>in</strong> N z potekata skozi strižno središče S, je torzijski moment M xS na točko S enak nič<br />
M xS = 0,<br />
na težišče T p prečnega prereza pa je enak (slika 1.94b)<br />
∫<br />
A x<br />
(y σ xz − z σ xy ) dA x = y S N z − z S N y .<br />
V primeru, da ima prečni prerez simetrijsko os, leži strižno središče S na tej osi. †<br />
strižnega središča podajamo v razdelku 2.6.<br />
Enačbe za račun<br />
<strong>1.3</strong>.1 Primeri<br />
Primer 1.25 Določimo strižni <strong>napetosti</strong> σ xy <strong>in</strong> σ xz zaradi prečne sile N z za prečni prerez pravokotne<br />
oblike s šir<strong>in</strong>o b <strong>in</strong> viš<strong>in</strong>o h ter za prečni prerez krožne oblike! Iz enačb (1.192) <strong>in</strong> (1.193) za P ∗ x = 0,<br />
P x = 0, M y = 0, N y = 0 <strong>in</strong> M z = 0 sledi<br />
Za določitev σ xy tako potrebujemo le S ∗ y(y ∗ ).<br />
Prečni prerez pravokotne oblike<br />
σ xy (y ∗ ) = − N z S ∗ y(y ∗ )<br />
h ∗ (y ∗ ) I y<br />
, σ xz (z ∗ ) = − N z S ∗ y(z ∗ )<br />
b ∗ (z ∗ ) I y<br />
.<br />
Pri računu statičnega momenta S ∗ y dela prečnega prereza A ∗ x dvojni <strong>in</strong>tegral (enačba (1.190)) prevedemo<br />
na enojnega, če upoštevamo, da je dA x = a dz (slika 1.95).<br />
S ∗ y(y ∗ ) =<br />
∫<br />
A ∗<br />
x<br />
z dA x =<br />
∫h/2<br />
−h/2<br />
( ) b<br />
z<br />
2 + y∗ dz =<br />
( ) b z<br />
2<br />
2 + h/2<br />
y∗ 2 ∣<br />
−h/2= 1 ( ) ( b h<br />
2<br />
2 2 + y∗<br />
† I.S. Sokolnikoff, Mathematical Theory of Elasticity, McGraw-Hill, New York, 1956.<br />
4 − h2<br />
4<br />
)<br />
= 0.
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 125<br />
Slika 1.95: Del prereza A ∗<br />
x za račun statičnega momenta S ∗ y(y ∗ )<br />
Sledi, da je strižna napetost σ xy povsod v prerezu enaka nič<br />
σ xy = 0.<br />
Velja splošno pravilo, da je σ xy zaradi prečne sile N z enaka nič, če ima prerez dve pravokotni osi<br />
simetrije. Takim prerezom pravimo, da so dvojnosimetrični. Račun <strong>napetosti</strong> σ xz dobimo z enačbo<br />
(1.193). V njej upoštevamo, da je P ∗ x = P x = M y = N y = 0. Za določitev σ xz tako potrebujemo<br />
le S ∗ y(z ∗ ). Pri računu statičnega momenta dela prečnega prereza A ∗ x dvojni <strong>in</strong>tegral prevedemo na<br />
enojnega, če upoštevamo, da je dA x = b dz (glej sliko 1.96).<br />
Slika 1.96: Del prereza A ∗<br />
x za račun statičnega momenta S ∗ y(z ∗ )<br />
S ∗ y(z ∗ ) =<br />
∫<br />
A ∗<br />
x<br />
z dA x =<br />
∫ z∗<br />
−h/2<br />
z b dz = b 2 z2 ∣ ∣∣∣<br />
z ∗<br />
−h/2= b 2<br />
)<br />
(z ∗ 2 − h2<br />
.<br />
4<br />
Če upoštevamo, da je<br />
b ∗ (z) ≡ b,<br />
I y = b h3<br />
12 ,
126 1 Upogib z osno silo<br />
sledi, da je strižna napetost σ xz enaka<br />
σ xz (z ∗ ) = − 6 N ( )<br />
z<br />
b h 3 z ∗ 2 − h2<br />
.<br />
4<br />
Strižna napetost σ xz je kvadratna funkcija koord<strong>in</strong>ate z. Lego ekstremne vrednosti strižne <strong>napetosti</strong> σ xz<br />
dobimo iz pogoja za ekstrem funkcije<br />
dσ xz<br />
dz ∗<br />
Velikost ekstremne vrednosti <strong>napetosti</strong> σ xz je<br />
= −6 N z<br />
b h 3 2 z∗ ekst = 0 → z∗ ekst = 0.<br />
σ xz (zekst ∗ ) = 3 N z<br />
2 b h = 1.5 N z<br />
.<br />
A x<br />
Sprem<strong>in</strong>janje strižne <strong>napetosti</strong> σ xz po viš<strong>in</strong>i prečnega prereza prikazujemo na sliki 1.97.<br />
Slika 1.97: Sprem<strong>in</strong>janje strižne <strong>napetosti</strong> σ xz po prečnem prerezu nosilca<br />
Prečni prerez krožne oblike s polmerom R<br />
Na sliki 1.98 označimo del prečnega prereza krožne oblike s pozitivno zunanjo normalo z z A ∗ x , z<br />
negativno zunanjo normalo z pa z A ∗∗<br />
x .<br />
Ker je S ∗ y(y) = 0, je strižna napetost σ xy enaka nič. Za račun strižne <strong>napetosti</strong> σ xz potrebujemo<br />
I y = π R4<br />
4 , R2 =<br />
( ) b(z) 2<br />
+ z 2 , b(z) = √ R 2 − z 2 ,<br />
2<br />
∫ R<br />
Sy ∗∗ = z b(z) dz =<br />
z ∗<br />
∫ R<br />
z ∗<br />
2 z √ R 2 − z 2 dz.
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 127<br />
Slika 1.98: Strižno napetost σ xz določamo pri z = z r<br />
Vpeljemo novo spremenljivko u = √ R 2 − z 2 <strong>in</strong> dobimo<br />
Določimo še u pri z ∗ <strong>in</strong> R:<br />
Statični moment S ∗∗<br />
y<br />
du = 1 2<br />
1<br />
dz<br />
√ (−2 z) dz = −z<br />
R 2 − z2 u .<br />
z = z ∗ → u = √ R 2 − (z ∗ ) 2 , z = R → u = 0.<br />
je<br />
S ∗∗<br />
y (z ∗ ) =<br />
∫ 0<br />
√<br />
R 2 −(z ∗ ) 2<br />
(<br />
2 z u − u du ) = −2 u3<br />
0<br />
z 3 ∣√ = 2<br />
R 2 −(z ∗ )<br />
3 2<br />
√<br />
(R 2 − (z ∗ ) 2 ) 3 .<br />
Strižna napetost σ xz je<br />
√<br />
σ xz (z ∗ ) = N z 2 (R 2 − (z ∗ ) 2 ) 3 4<br />
3 · 2 √ R 2 − (z ∗ ) 2 π R = 4 N z (<br />
R 2 4 3 π R 4 − (z ∗ ) 2) .<br />
Napetost σ xz ima ekstremno vrednost pri z = 0<br />
σ xz,ekst =<br />
4 N z<br />
3 π R 2 = 4 N z<br />
. (1.194)<br />
3 A x<br />
Na sliki 1.99 prikazujemo potek strižne <strong>napetosti</strong> σ xz (N z ) za prečni prerez krožne oblike.
128 1 Upogib z osno silo<br />
Slika 1.99: Strižna napetost σ xz za prečni prerez krožne oblike<br />
Primer 1.26 Določimo diagram strižnih <strong>napetosti</strong> zaradi prečne sile N z = 10 kN za na sliki prikazani<br />
prerez oblike črke T (slika 1.100)!<br />
Slika 1.100: Prečni prerez v obliki črke T<br />
Enačbi za račun <strong>napetosti</strong> σ xy <strong>in</strong> σ xz dobimo iz (1.192) <strong>in</strong> (1.193)<br />
σ xy (N z ) = − N z S ∗ y(y ∗ )<br />
h ∗ (y ∗ ) I y<br />
, σ xz (N z ) = − N z S ∗ y(z ∗ )<br />
b ∗ (z ∗ ) I y<br />
.<br />
Koord<strong>in</strong>atni osi y <strong>in</strong> z morata potekati skozi težišče prečnega prereza. Ker njegove lege še ne poznamo,<br />
za njegov račun izberemo tak koord<strong>in</strong>atni sistem, v katerem račun poteka dovolj preprosto. Uporabimo<br />
koord<strong>in</strong>atni sistem y ′ , z ′ , kot kaže slika 1.101. Zaradi simetrije prereza težišče leži na osi z ′ oziroma<br />
y ′ T = 0. y ′ T = 0, z ′ T =<br />
15 · 8 · 4 + 15 · 8 · 15.5<br />
2 · 15 · 8<br />
= 9.75 cm.
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 129<br />
Slika 1.101: Koord<strong>in</strong>ati težišča računamo v koord<strong>in</strong>atnem sistemu y ′ , z ′<br />
Vztrajnostni moment I y glede na glavno vztrajnostno os y v težišču prereza (slika 1.102)<br />
I y =<br />
15 · 83<br />
12<br />
+ 5.75 2 · 8 · 15 + 8 · 153<br />
12<br />
+ 5.75 2 · 8 · 15 = 10825 cm 4 .<br />
Slika 1.102: Koord<strong>in</strong>ate težišč posameznih likov za račun vztrajnostnega momenta<br />
Črte vzdolž katerih računamo σ xy so navpične. Oblika dela prečnega prereza se nezvezno spremeni pri<br />
y = −4 <strong>in</strong> pri y = 4. Zato za račun statičnega momenta S ∗ y(y) za del prereza A ∗ x ločimo tri <strong>in</strong>tegracijska<br />
območja. Delni prerez A ∗ x za območje −7.5 ≤ y ∗ ≤ −4.0 je prikazan na sliki 1.103<br />
S ∗ y(y ∗ ) =<br />
∫ y∗<br />
−7.5<br />
−5.75 · 8 dy = −8 · 5.75 y∣ y∗<br />
= −46 −7.5 (y∗ + 7.5) = −345 − 46 y ∗ [cm 3 ].
130 1 Upogib z osno silo<br />
Slika 1.103: Integracijsko območje −7.5 ≤ y ∗ ≤ −4.0<br />
Delni prerez A ∗ x za območje −4.0 ≤ y ∗ ≤ 4.0 je prikazan na sliki 1.104<br />
S ∗ y(y ∗ ) =<br />
∫−4<br />
−5.75 · 8 dy +<br />
∫ y∗<br />
1.75 · 23 dy = −46 (−4 + 7.5) + 40.25 (y ∗ + 4) = 40.25 y ∗ [cm 3 ].<br />
−7.5<br />
−4<br />
Slika 1.104: Integracijsko območje −4.0 ≤ y ∗ ≤ 4.0<br />
Delni prerez A ∗ x za območje 4.0 ≤ y ∗ ≤ 7.5 je prikazan na sliki 1.105<br />
S ∗ y(y ∗ ) =<br />
∫−4<br />
∫ 4<br />
−5.75 · 8 dy +<br />
1.75 · 23 dy +<br />
∫ y∗<br />
−5.75 · 8 dy =<br />
−7.5<br />
−4<br />
4<br />
= −161 + 40.25 · 8 − 46 (y ∗ − 4) = 345 − 46 y ∗ [cm 3 ].
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 131<br />
Slika 1.105: Integracijsko območje 4.0 ≤ y ∗ ≤ 7.5<br />
Za račun statičnega momenta Sy(z ∗ ∗ ) za del prereza Ax<br />
∗ ločimo dve <strong>in</strong>tegracijski območji, saj se pri<br />
vodoravnih črtah, vzdolž katerih računamo napetost σ xz , delni prerez nezvezno spremeni le pri z =<br />
−1.75. Delni prerez Ax ∗ za območje −9.75 ≤ z ∗ ≤ −1.75 je prikazan na sliki 1.106<br />
S ∗ y(z ∗ ) =<br />
∫ z∗<br />
−9.75<br />
z · 15 dz = 7.5 z 2 ∣ ∣∣<br />
z ∗<br />
−9.75 = 7.5 ( (z ∗ ) 2 − 9.75 2) = 7.5 (z ∗ ) 2 − 712.97 [cm 3 ].<br />
Slika 1.106: Integracijsko območje −9.75 ≤ z ∗ ≤ −1.75<br />
Delni prerez A ∗ x za območje −1.75 ≤ z ∗ ≤ 13.25 je prikazan na sliki 1.107<br />
−1.75 ∫<br />
Sy(z ∗ ∗ ) = z·15 dz+<br />
∫ z∗<br />
−9.75<br />
−1.75<br />
Strižno napetost σ xz izračunamo po enačbi<br />
z·8 dz = 7.5 (1.75 2 −9.75 2 )+4 ( (z ∗ ) 2 − 1.75 2) = 4 (z ∗ ) 2 −702.25[cm 3 ].<br />
N z<br />
σ xz (z ∗ ) = −<br />
b ∗ (z ∗ (4 (z ∗ ) 2 − 702.25).<br />
) I y<br />
(1.195)
132 1 Upogib z osno silo<br />
Slika 1.107: Integracijsko območje −1.75 ≤ z ∗ ≤ 13.25<br />
Ekstremno vrednost strižne <strong>napetosti</strong> σ xz izračunamo z odvajanjem dσ xz /dz ∗ = 0:<br />
−1.75 ≤ z ∗ ≤ 13.25 :<br />
dσ xz<br />
dz ∗<br />
= N z<br />
8 I y<br />
8 z ∗ = 0 → z ∗ ekst = 0 → σ xz,ekst = 81.7 N/cm 2 .<br />
Velikosti strižnih <strong>napetosti</strong> σ xy <strong>in</strong> σ xz podajamo v preglednicah 1.18 <strong>in</strong> 1.19, grafični prikaz pa na sliki<br />
1.108. Vidimo, da se σ xy v odvisnosti od y sprem<strong>in</strong>ja odsekoma l<strong>in</strong>earno <strong>in</strong> je na mestih, kjer se prerez<br />
nezvezno spremeni, nezvezna. Napetost σ xz se sprem<strong>in</strong>ja po kvadratni paraboli v odvisnosti od z. Pri<br />
z = −1.75, kjer se šir<strong>in</strong>a prereza nezvezno spremeni, je tudi σ xz nezvezna. Največja vrednost σ xz =<br />
81.7 N/cm 2 je pri z = 0.<br />
Tabela 1.18: Strižna napetost σ xy (y)<br />
y ∗ [cm] h ∗ [cm] σ xy [N/cm 2 ]<br />
-7.5 8 0<br />
-4.0 8 18.59<br />
-4.0 23 6.47<br />
0 23 0<br />
4.0 23 -6.47<br />
4.0 8 -18.59<br />
7.5 8 0
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 133<br />
Tabela 1.19: Strižna napetost σ xz (z)<br />
z ∗ [cm] b ∗ [cm] σ xz [N/cm 2 ]<br />
-9.75 15 0<br />
-1.75 15 42.5<br />
-1.75 8 79.7<br />
0 8 81.7<br />
13.25 8 0<br />
Slika 1.108: Potek strižnih <strong>napetosti</strong> σ xy <strong>in</strong> σ xz<br />
Posledica predpostavke, da se strižni <strong>napetosti</strong> σ xy <strong>in</strong> σ xz ne sprem<strong>in</strong>jata vzdolž y oziroma z osi je, da<br />
niso izpolnjeni robni pogoji (slika 1.109).<br />
Na sliki 1.109a vidimo, da je napetost σ xz vzdolž vodoravnega roba z = −1.75 različna od nič, čeprav<br />
je ta rob neobremenjen <strong>in</strong> iz ravnotežne enačbe na robu sledi, da je σ xz = 0. Podobno iz slike 1.109b<br />
sledi, da je σ xy vzdolž navpičnih robov različna od nič, čeprav ta robova nista strižno obremenjena <strong>in</strong><br />
iz robnih pogojev sledi, da je σ xy = 0. Kljub tej pomanjkljivosti sta podani enačbi dovolj natančni za<br />
oceno strižnih <strong>napetosti</strong> v l<strong>in</strong>ijskih konstrukcijah <strong>in</strong> se v praksi redno uporabljajo.
134 1 Upogib z osno silo<br />
Slika 1.109: Zaradi privzetih predpostavk robni pogoji niso izpolnjeni<br />
Primer 1.27 Z uporabo ravnotežne enačbe za del nosilca na sliki 1.110 izpeljimo enačbo za račun<br />
strižne <strong>napetosti</strong> σ xz . Predpostavimo ravn<strong>in</strong>sko napetostno stanje v ravn<strong>in</strong>i x, z. Ploskev A z je vzporedna<br />
ravn<strong>in</strong>i x, y.<br />
Slika 1.110: Iz nosilca v ravn<strong>in</strong>i x, z, na katerega deluje navpična obtežba, izrežemo del nosilca<br />
dolž<strong>in</strong>e dx s prečnim prerezom A ∗<br />
x<br />
Vzemimo, da na nosilec v ravn<strong>in</strong>i x, z delujejo zunanje sile pravokotno na vzdolžno os nosilca, to je v<br />
smeri osi z. Prečni prerez A x nosilca se vzdolž osi nosilca ne sprem<strong>in</strong>ja. Oblika prečnega prereza naj<br />
ima simetrijsko os, ki sovpada z osjo z. V tem primeru računamo vzdolžno normalno napetost σ xx po<br />
enačbi<br />
σ xx = M y<br />
I y<br />
z. (1.196)<br />
V nadaljevanju predpostavimo, da se velikost strižne <strong>napetosti</strong> σ xz vzdolž premic, ki so vzporedne osi y,<br />
ne sprem<strong>in</strong>ja. Na sliki 1.111 prikazujemo <strong>napetosti</strong>, ki na obravnavani del telesa delujejo.
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 135<br />
Slika 1.111: Na izrezani del nosilca delujeta normalna <strong>in</strong> strižna napetost<br />
Izraz za strižno napetost σ xz izpeljemo, če za sile na sliki 1.111 zapišemo ravnotežni pogoj ∑ X = 0.<br />
Pri tem upoštevamo, da na prečni prerez Ax1 ∗ deluje normalna napetost σ xx, na prečni prerez Ax2 ∗ pa<br />
σ xx + dσ xx . V ploskvici, ki je vzporedna ravn<strong>in</strong>i x, y, deluje vzdolž robu x konstantna strižna napetost<br />
σ zx , vzdolž robu x + dx pa konstantna strižna napetost σ zx + dσ zx . Srednja (povprečna) strižna napetost<br />
v tej ploskvici je zato σ zx + (1/2) dσ zx . Ravnotežni pogoj zapišemo z enačbo:<br />
∫<br />
(<br />
− σ xx dA x + σ zx + 1 )<br />
∫<br />
2 dσ zx b ∗ (z) dx + (σ xx + dσ xx ) dA x = 0. (1.197)<br />
A ∗<br />
x1<br />
Upoštevamo enčbo (1.196) ter zvezo dM y /dx = N z<br />
σ xx + dσ xx = M y<br />
z + d ( )<br />
My<br />
z dx = M y<br />
I y dx I y I y<br />
<strong>in</strong> dobimo<br />
− M y<br />
I y<br />
∫<br />
A ∗<br />
x1<br />
A ∗<br />
x2<br />
z + dM y<br />
dx<br />
z dA x + σ zx b ∗ (z) dx + 1 2 dσ zx b ∗ (z) dx + M y<br />
I y<br />
z<br />
dx = M y<br />
z + N z<br />
z dx. (1.198)<br />
I y I y I y<br />
∫<br />
A ∗<br />
x2<br />
z dA x + N z<br />
I y<br />
dx<br />
∫<br />
A ∗<br />
x2<br />
z dA x = 0.<br />
Če upoštevamo še, da sta ploskvi Ax1 ∗ <strong>in</strong> A x2 ∗ enaki <strong>in</strong> če zanemarimo kvadrat diferencialnih količ<strong>in</strong><br />
(dσ zx dx), sledi<br />
σ zx b ∗ (z) dx + N ∫<br />
z<br />
dx z dA x = 0.<br />
I y<br />
Upoštevamo še, da je σ zx = σ xz <strong>in</strong> dobimo<br />
Z S ∗ y je označen statični moment delnega prereza A ∗ x .<br />
A ∗<br />
x<br />
σ xz = − N z S ∗ y<br />
b ∗ (z) I y<br />
. (1.199)
136 1 Upogib z osno silo<br />
Primer 1.28 Izračunajmo največjo strižno napetost v vijaku v konstrukciji na sliki 1.112. Nosilec med<br />
točkama AC je sestavljen iz dveh delov, med točkama BC pa iz enega dela. Polmer r prečnega prereza<br />
vijaka ima velikost 1 cm, sila F = 5 kN, razdalja a pa 1 m.<br />
Slika 1.112: Nosilec AC je sestavljen iz dveh delov, nosilec BC pa iz enega dela<br />
Reakcije <strong>in</strong> sile v vezi izračunamo iz ravnotežnih pogojev (slika 1.113).<br />
Slika 1.113: Vpliv podpor nadomestimo z reakcijami, vez pa izrežemo<br />
Ravnotežni pogoji:<br />
Členek:<br />
C l x = C d x, C l z = C d z .<br />
Iz momentnega pogoja na členek v podpori A za celo konstrukcijo dobimo, da je B z = −F , iz pogoja<br />
∑ Z = 0 za celo konstrukcijo sledi Az = −F , iz momentnega ravnotežnega pogoja na členek C za levi<br />
del konstrukcije A x = F/4, iz pogojev ∑ X = 0 <strong>in</strong> ∑ Z = 0 za levi del pa C l x = −F/4 <strong>in</strong> C l z = 0. Na<br />
sliki 1.114 so prikazane sile na vijak. Upoštevano je, da je nosilec AC iz dveh delov.
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 137<br />
Slika 1.114: Sile, ki na vijak delujejo<br />
Na prečni prerez vijaka deluje prečna sila Q velikosti F/8. Največja strižna napetost v vijaku je (enačba<br />
(1.194))<br />
τ max = 4 3<br />
Q<br />
π r 2 = 4 3<br />
5<br />
8 π 1 2 = 0.265 kN/cm2 .<br />
Primer 1.29 Določimo velikost strižne sile F s , ki uč<strong>in</strong>kuje na prvo zakovico prostoležečega nosilca,<br />
sestavljenega iz dveh tračnic! Nosilec je obremenjen z enakomerno obtežbo q = 18 kN/m. Plošč<strong>in</strong>a<br />
prereza tirnice je A x = 55.6 cm 2 , vztrajnostni moment tirnice na težišče prereza je Iy T = 1476 cm 4 ,<br />
oddaljenost težišča z<br />
T ′ = 6.96 cm. Dolž<strong>in</strong>a nosilca je L = 6.5 cm, razdalja e med zakovicami pa 15 cm<br />
(slika 1.115). Določimo tudi potrebni premer prve zakovice! Največja dovoljena strižna napetost τ max v<br />
zakovici je τ max = 4 kN/cm 2 .<br />
Slika 1.115: Nosilec je sestavljen iz dveh tračnic, ki sta med seboj povezani z zakovicami<br />
Pri računu predpostavimo, da se zakovičen nosilec obnaša tako, kot da bi bil prerez nosilca homogen.<br />
Na sliki 1.116 je prikazano deformiranje dveh nepovezanih <strong>in</strong> dveh povezanih nosilcev. Slika 1.116a<br />
prikazuje primer, ko tirnici nista povezani, med njima pa ni trenja. Slika 1.116b prikazuje togo povezani<br />
tirnici. Taki tirnici sta po vsej dolž<strong>in</strong>i zavarjeni. Zakovičeni tirnici nista povsem togo povezani. Vendar<br />
je njuno obnašanje bližje drugemu primeru.<br />
Če se nosilec obnaša, kot da je iz enega samega dela, izračunamo <strong>napetosti</strong> σ xz = σ zx zaradi prečne sile<br />
N z po enačbi<br />
σ xz (N z ) = − N z S ∗ y(z ∗ )<br />
b ∗ (z ∗ ) I y<br />
.
138 1 Upogib z osno silo<br />
Slika 1.116: Deformirani legi nepovezanih <strong>in</strong> togo povezanih tračnic<br />
Strižno silo F s , ki jo morata “prevzeti” prvi dve zakovici, približno določimo, če <strong>in</strong>tegriramo strižno<br />
napetost σ zx po ravn<strong>in</strong>i A s (x, y) pri z = 0 na dolž<strong>in</strong>i 0 ≤ x ≤ e (slika 1.117)<br />
∫<br />
∫<br />
2F s = σ zx dA s = σ xz dA s .<br />
A s A s<br />
Slika 1.117: Območje stika med tračnicama, ki pripada prvima dvema zakovicama<br />
Integral po ploskvi lahko prevedemo na enojni <strong>in</strong>tegral tako, da upoštevamo dA s = b ∗ (z = 0) dx<br />
2F s =<br />
∫ e<br />
0<br />
− N z S ∗ y(z = 0)<br />
b ∗ (z = 0) I y<br />
∫ e<br />
b ∗ (z = 0) dx = −<br />
0<br />
N z Sy(z ∗ = 0)<br />
dx.<br />
Izračunati moramo prečno silo N z v odvisnosti od koord<strong>in</strong>ate x, statični moment dela prereza za z = 0<br />
<strong>in</strong> vztrajnostni moment glede na os y.<br />
I y
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 139<br />
Račun prečne sile (slika 1.118):<br />
N z (x) = −A z − q x = q L 2 − q x = 0.18 ( 650<br />
2 − x )<br />
= 0.18 (325 − x).<br />
Slika 1.118: Statični model za račun prečne sile N z<br />
Račun statičnega momenta dela prereza S ∗ y(z = 0):<br />
Račun vztrajnostnega momenta I y glede na os y:<br />
Strižna sila, ki jo prevzameta dve zakovici, je<br />
S ∗ y(z = 0) = −6.96 · 55.6 = −386.98 cm 3 .<br />
I y = 2 (1476 + 6.96 2 · 55.6) = 8338.71 cm 4 .<br />
2F s =<br />
∫ 15<br />
na eno zakovico pa deluje polovična sila<br />
0<br />
0.18 (325 − x) 386.98 dx = 39.78 kN,<br />
8338.71<br />
F s = 39.78<br />
2<br />
Določimo prerez zakovice (dimenzioniranje zakovice).<br />
= 19.89 kN.<br />
Zakovica ima krožni prerez polmera R. Največja strižna napetost je (glej (1.194))<br />
σ max<br />
F s<br />
xz = 4 3 π R 2<br />
<strong>in</strong> mora biti manjša ali enaka največji dovoljeni strižni <strong>napetosti</strong><br />
σ max<br />
xz ≤ τ max .
140 1 Upogib z osno silo<br />
Iz te neenačbe izračunamo pogoj, ki mu mora ustrezati polmer zakovice<br />
√<br />
4<br />
R ≥<br />
3<br />
F s<br />
π τ max<br />
=<br />
√<br />
4<br />
3<br />
19.89<br />
4 π<br />
= 1.453 cm,<br />
premer D zakovice pa mora ustrezati pogoju<br />
D = 2 R ≥ 2.91 cm.<br />
Primer <strong>1.3</strong>0 Določimo prečno normalno napetost σ zz v <strong>nosilcu</strong> z ravno osjo <strong>in</strong> pravokotnim prečnim<br />
prerezom (slika 1.119). Prečni prerez je obtežen s prečno silo N z ter upogibnim momentom M y .<br />
Slika 1.119: Prečni prerez pravokotne oblike šir<strong>in</strong>e b <strong>in</strong> viš<strong>in</strong>e h<br />
Prečno normalno napetost izračunamo po enačbi (1.177)<br />
σ zz = − 1<br />
b ∗ (z ∗ )<br />
V obravnavanem primeru je (p z [N/cm 2 ])<br />
b ∗ (z ∗ ) = b,<br />
⎛<br />
⎜<br />
⎝P ∗<br />
z (x) +<br />
∫<br />
A ∗<br />
x (x)<br />
∂σ xz<br />
σ xz = − 6 N ( )<br />
z<br />
b h 3 z 2 − h2<br />
, Pz ∗ =<br />
4<br />
⎞<br />
∂x dA ⎟<br />
x⎠ . (1.200)<br />
∫<br />
C ∗<br />
x,z<br />
p z ds = p z b<br />
<strong>in</strong><br />
∫<br />
P z =<br />
p z ds = p z b = P ∗<br />
z ,<br />
dA x = b dz,<br />
dN z<br />
dx + P z = 0.<br />
C x
<strong>1.3</strong> Strižni <strong>in</strong> prečni <strong>normalni</strong> <strong>napetosti</strong> v <strong>nosilcu</strong> s <strong>konstantnim</strong> prečnim prerezom 141<br />
Tako dobimo<br />
σ zz = − 1 b<br />
= − 1 b<br />
⎛<br />
⎜<br />
⎝P ∗<br />
z +<br />
⎛<br />
∫<br />
A ∗<br />
x<br />
⎜<br />
⎝P z + 6 P z<br />
b h 3<br />
(<br />
− 6 dN z<br />
b h 3 dx<br />
∫z<br />
−h/2<br />
= − P b − 6 P ( )<br />
z<br />
3<br />
b h 3 3 − h2<br />
4 z − h3<br />
12<br />
)) (z ⎞ 2 − h2 ⎟ ⎠ =<br />
4<br />
⎞<br />
) (¯z 2 − h2 ⎟<br />
b d¯z ⎠ =<br />
4<br />
= − 6 P ( )<br />
z z<br />
3<br />
b h 3 3 − h2<br />
4 z + h3<br />
.<br />
12<br />
Vrednosti prečne normalne <strong>napetosti</strong> σ zz za z = −h/2, z = 0 <strong>in</strong> z = h/2:<br />
σ zz (−h/2) = − P z<br />
b ,<br />
σ zz(0) = − P z<br />
2 b , σ zz(h/2) = 0.<br />
Na sliki 1.120 prikazujemo potek prečne normalne <strong>napetosti</strong> σ zz .<br />
Slika 1.120: Potek prečne normalne <strong>napetosti</strong> σ zz a<br />
Določimo še razmereje med največjo prečno normalno napetostjo σ zz,max = σ zz (−h/2) ter največjo<br />
vzdolno normalno napetostjo σ xx,max za prostoležeči nosilec pravokotnega prereza, na katerega deluje<br />
enakomerna l<strong>in</strong>ijska obtežba P z .<br />
Največja vzdolžna normalna napetost je (z L je označena dolž<strong>in</strong>a nosilca)<br />
σ xx,max = M max<br />
W y<br />
= P z L 2 6<br />
b h 2 = 3 P z L 2<br />
b h 2 .<br />
Po absolutni vrednosti največja prečna normalna napetost je |σ zz,max | = P z /b. Razmerje med prečno<br />
normalno <strong>in</strong> vzdolžno normalno napetostjo je<br />
|σ zz,max |<br />
= 4 ( ) h 2<br />
.<br />
σ xx,max 3 L
142 1 Upogib z osno silo<br />
Za l<strong>in</strong>ijski nosilec, pri katerem je h/L = 0.1 dobimo<br />
|σ zz,max | = 4<br />
300 σ xx,max.<br />
V tem primeru znaša prečna normalna napetost <strong>1.3</strong>3% vzdolžne normalne <strong>napetosti</strong>. Zaradi teg pri<br />
l<strong>in</strong>ujskih nosilcih prečne normalne <strong>napetosti</strong> največkrat zanemarimo.<br />
1.4 Glavne normalne <strong>napetosti</strong> v <strong>nosilcu</strong><br />
Napetosti σ xx , σ zz <strong>in</strong> σ xz določajo ravn<strong>in</strong>sko napetostno stanje v ravn<strong>in</strong>i x, z. Napetostni vektor ⃗σ N v<br />
prerezu z zunanjo normalo ⃗e N lahko izrazimo z napetostnima vektorjema ⃗σ x <strong>in</strong> ⃗σ z , ki pripadata ravn<strong>in</strong>am<br />
z zunanjima normalama ⃗e x <strong>in</strong> ⃗e z (slika 1.121)<br />
⃗σ N = ⃗σ x e Nx + ⃗σ z e Nz .<br />
Slika 1.121: Prerez nosilca z zunanjo normalo ⃗e N<br />
Če je α kot med vektorjema ⃗e x <strong>in</strong> ⃗e N , zapišemo normalno napetost σ NN <strong>in</strong> strižno napetost σ NT z<br />
enačbama<br />
σ NN = σ xx + σ zz<br />
2<br />
σ NT = σ xx − σ zz<br />
2<br />
+ σ xx − σ zz<br />
2<br />
cos 2 α − σ xz s<strong>in</strong> 2 α, (1.201)<br />
s<strong>in</strong> 2 α + σ xz cos 2 α, (1.202)<br />
ki ju izpeljemo na enak nač<strong>in</strong> kot v razdelku 2.6.1 v učbeniku: M. Stanek, G. Turk, Osnove mehanike<br />
trdnih teles, Univerza v Ljubljani. Ekstremno vrednost <strong>normalni</strong>h <strong>napetosti</strong> določa kot α σ (glej razdelek<br />
2.6.2 v istem učbeniku)<br />
tg 2 α σ =<br />
2 σ xz<br />
, (1.203)<br />
σ zz − σ xx<br />
ekstremno vrednost strižnih <strong>napetosti</strong> pa kot α τ<br />
Velikosti ekstremnih <strong>napetosti</strong> lahko izračunamo z enačbama<br />
tg 2 α τ = − σ zz − σ xx<br />
2 σ xz<br />
. (1.204)<br />
σ 11,22 = σ xx + σ zz<br />
2<br />
√ (σzz )<br />
− σ 2<br />
xx<br />
±<br />
+ σ<br />
2<br />
xz, 2 (1.205)
1.4 Glavne normalne <strong>napetosti</strong> v <strong>nosilcu</strong> 143<br />
velikosti ekstremnih strižnih <strong>napetosti</strong> pa po enačbah<br />
√ (σzz<br />
− σ xx<br />
τ II = ±<br />
2<br />
) 2<br />
+ σ 2 xz = ± 1 2 (σ 11 − σ 22 ). (1.206)<br />
Pri grednih nosilcih prečno normalno napetost σ zz običajno zanemarimo. Zato se enačbe (1.201) -<br />
(1.206) poenostavijo.<br />
Ekstremno vrednost <strong>normalni</strong>h <strong>napetosti</strong> določa kot α σ<br />
ekstremno vrednost strižnih <strong>napetosti</strong> pa kot α τ<br />
Velikosti ekstremnih <strong>napetosti</strong> lahko izračunamo z enačbama<br />
σ NN = σ xx<br />
2 + σ xx<br />
2 cos 2 α − σ xz s<strong>in</strong> 2 α (1.207)<br />
σ NT = σ xx<br />
2 s<strong>in</strong> 2 α + σ xz cos 2 α. (1.208)<br />
tg 2 α σ = − 2 σ xz<br />
σ xx<br />
, (1.209)<br />
tg 2 α τ = σ xx<br />
2 σ xz<br />
. (1.210)<br />
σ 11 = σ max = 1 2 [σ xx + √ σ 2 xx + 4 σ 2 xz],<br />
σ 22 = σ m<strong>in</strong> = 1 2 [σ xx − √ σ 2 xx + 4 σ 2 xz],<br />
(1.211)<br />
velikosti ekstremnih strižnih <strong>napetosti</strong> pa po enačbah<br />
τ II = ± 1 2√<br />
σ 2 xx + 4 σ 2 xz = ± 1 2 (σ 11 − σ 22 ). (1.212)<br />
Z uporabo enačb (1.209) <strong>in</strong> (1.211) lahko določimo v vseh točkah (x, z) l<strong>in</strong>ijskega nosilca smeri <strong>in</strong><br />
velikosti glavnih <strong>normalni</strong>h <strong>napetosti</strong> <strong>in</strong> narišemo dve skup<strong>in</strong>i med seboj pravokotnih krivulj, katerih<br />
tangente se v vsaki točki (x, z) nosilca ujemajo z eno od glavnih ravn<strong>in</strong> za to točko. Te krivulje imenujemo<br />
trajektorije glavnih <strong>napetosti</strong>.<br />
Trajektorije glavnih <strong>normalni</strong>h <strong>napetosti</strong> določimo z uporabo enačbe (1.209), v kateri upoštevamo, da sta<br />
σ xx <strong>in</strong> σ xz funkciji koord<strong>in</strong>at x <strong>in</strong> z<br />
Enačbo (1.213) izrazimo v odvisnosti od tg 2 α σ<br />
tg 2 α σ =<br />
tg 2 α σ = − 2 σ xz(x, z)<br />
σ xx (x, z) . (1.213)<br />
2 tg α σ<br />
1 − tg 2 α σ<br />
= f(x, z) → f(x, z) tg 2 α σ + 2 tg α σ − f(x, z) = 0
144 1 Upogib z osno silo<br />
<strong>in</strong> jo rešimo<br />
√<br />
tg α σ = − 1<br />
f(x, z) ± 1<br />
1 +<br />
f 2 (x, z) .<br />
Posamezna trajektorija glavnih <strong>normalni</strong>h <strong>napetosti</strong> je funkcija z(x). Če upoštevamo, da je odvod dz/dx<br />
enak tg α σ , ter namesto f(x, y) zapišemo (1.213), dobimo<br />
√<br />
dz<br />
dx = σ xx(x, z)<br />
2 σ xz (x, z) ± 1 + σ2 xx(x, z)<br />
4 σxz(x, 2 z) . (1.214)<br />
Enačba (1.214) predstavlja diferencialno enačbo prvega reda, katere rešitev je funkcija z(x). Diferencialni<br />
enačbi prvega reda pripada en robni pogoj. Če vzamemo<br />
z(0) = k, (1.215)<br />
kjer je s k označena konstanta, dobimo eno izmed trajektorij. Različnim trajektorijam <strong>napetosti</strong> ustrezajo<br />
različne vrednosti robnega pogoja z(0) = k. Diferencialno enačbo (1.214) z robnim pogojem (1.215)<br />
lahko rešimo numerično (na primer s programom Mathematica ali Matlab).<br />
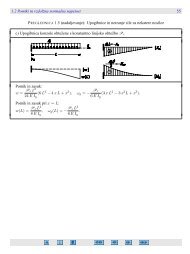
Primer <strong>1.3</strong>1 Določimo trajektorije glavnih <strong>normalni</strong>h <strong>napetosti</strong> v konzolnem <strong>nosilcu</strong> dolž<strong>in</strong>e L = 3 m,<br />
viš<strong>in</strong>e h = 1 m <strong>in</strong> šir<strong>in</strong>e b = 20 cm, ki je obtežen s silo F = 1 kN na prostem koncu konzole pri x = L!<br />
Notranje sile v obravnavani konstrukciji so<br />
N x (x) = 0, N z (x) = F, M y (x) = −F (L − x).<br />
Normalno napetost σ xx izračunamo po enačbi (1.89), strižno napetost σ xz pa po enačbi (1.193)<br />
σ xx (x, z) = M y(x)<br />
I y<br />
σ xz (x, z) = − N z(x) S ∗ y<br />
b ∗ I y<br />
z = M y(x)<br />
b h 3<br />
12 F (L − x) z<br />
12 z = −<br />
b h 3 ,<br />
= − 6 F (<br />
b h 3 z 2 − h2<br />
4<br />
)<br />
.<br />
(1.216)<br />
Ob upoštevanju enačb (1.216) v diferencialni enačbi (1.214) smo z računalniškim programom določili<br />
potek trajektorij glavnih <strong>normalni</strong>h <strong>napetosti</strong>, ki jih prikazujemo na sliki 1.122.<br />
Slika 1.122: Potek trajektorij glavnih <strong>normalni</strong>h <strong>napetosti</strong> v konzoli