Čista torzija ravnega nosilca z zaprtim enoceličnim ... - FGG-KM

Čistatorzijaravneganosilcazzaprtimenoceličnim tankostenskim 

prečnim prerezom 

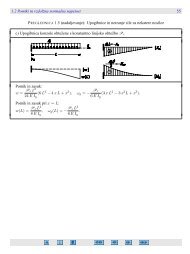
Razporeditev strižnih napetosti pri čisti torziji votlega eliptičnega prereza 

kaže, da največje napetosti nastopajo na zunanjem robu prereza, 

material v notranjosti prereza pa je napetostno slabo izkoriščen. Zato je 

za prenašanje torzijske obtežbe ugodno izbirati zaprte tankostenske prereze, 

pri katerih je material nameščen čim bolj ob zunanjem robu prereza. 

O tankostenskem zaprtem prečnem prerezu govorimo v primeru, 

da je stena zaprtega prereza zelo tanka v primerjavi z drugimi dimenzijami 

prereza, na primer z njegovo višino ali širino. Na (sliki T-1) je 

prikazan tankostenski prerez A x ,kigadoločata zunanja in notranja 

mejna krivulja C z in C n . Votli del prereza je označen z A n . 

Slika T-1 

Pri poljubno oblikovanem zaprtem profilu z neenakomerno debelino 

stene δ je ugodno namesto kartezijskih prereznih koordinat (y, z) vpeljati 

“naravni” koordinati (η, ζ). Pri tem je ζ ločna dolžina tako ime- 

1

Nosilec z zaprtim enoceličnim tankostenskim prečnim prerezom 

novane srednje črte prereza C s , ki poteka po sredini debeline stene in 

ograjuje srednjo ploskev A s .Koordinatiζ sta v vsaki točki srednje črte 

prirejena medsebojno pravokotna enotska bazna vektorja e η in e ζ ,prvi 

v smeri normale in drugi v smeri tangente na srednjo črto. Po analogiji 

z ozkim pravokotnim prerezom lahko tedaj vzamemo, da se napetostna 

funkcija ϕ vzdolž srednje krivulje C s , torej v odvisnosti od koordinate 

ζ, nespreminja 

∂ϕ 

∂ζ =0. 

(T.1) 

Pripadajoči strižni napetosti σ xη in σ xζ izrazimo z napetostno funkcijo 

ϕ po analogiji z enačbama (5.178) 

σ xη = θG ∂ϕ in σ xζ = −θG ∂ϕ 

∂ζ 

∂η . (T.2) 

Poissonova enačba čiste torzije se v koordinatah (η, ζ) glasi 

∂ 2 ϕ 

A x : 

∂η + ∂2 ϕ 

2 ∂ζ +2=0. 

(T.3) 

2 

Ob upoštevanju poenostavitve (T.1) iz prve od enačb (T.2) sledi, da je 

σ xη = 0 povsod na tankostenskem prerezu, Poissonova enačbapapreide 

v navadno diferencialno enačbo drugega reda glede na koordinato η 

Splošna rešitev te enačbe je 

∂ 2 ϕ 

∂η 2 = −2 . 

(T.4) 

ϕ = −η 2 + C 1 η + C 2 . 

(T.5) 

Integracijski konstanti C 1 in C 2 določimo iz pogoja, da mora biti vrednost 

napetostne funkcije na zunanjem robu prereza enaka nič, na notranjem 

robu pa enaka neki konstantni vrednosti ϕ n 

( 

ϕ η = − δ ) 

⎧ 

= ϕ n 

2 

⎪⎨ C 1 = − ϕ n 

δ 

( 

ϕ η = δ ) → 

⎪⎩ 

=0 

C 2 = 

ϕ n 

2 

2 + δ2 

4 

(T.6) 

2


Rešitev Poissonove diferencialne enačbejetorej 

ϕ = −η 2 − ϕ δ η + ϕ n 

2 + δ2 

4 . (T.7) 

Torzijski vztrajnostni moment I x določimo z enačbo (5.194), kjer 

upoštevamo, da imamo samo eno notranjo odprtino s ploščino A n ,kiji 

pripada konstantna vrednost napetostne funkcije ϕ n 

∫ 

I x =2 ϕdA x +2ϕ n A n . 

(T.8) 

A x 

Vprvemčlenu vzamemo dA x = dη dζ ter integriramo po ζ vzdolž sklenjene 

srednje črte C s in po η vmejahod−δ/2 do+δ/2 

∮ 

I x =2 

δ 

∫ 2 

C s − δ 2 

( 

−η 2 − ϕ δ η + ϕ ) 

n 

2 + δ2 

dη dζ +2ϕ n A n . 

4 

(T.9) 

A x 

Po izvrednotenju integrala po debelini stene sledi 

I x = 1 ∮ 

3 

∮ 

δ 3 dζ + ϕ n δdζ+2ϕ n A n . (T.10) 

C s 

C s 

Integral v drugem členu predstavlja ploščino materialnega dela prereza 

A x ∮ 

C s 

= δdζ, (T.11) 

zato lahko pišemo 

I x = 1 ∮ 

( 

δ 3 dζ +2ϕ n A n + A ) 

x 

. 

3 

2 

(T.12) 

C s 

Pri tankostenskem prerezu je izraz v oklepaju praktično enak ploščini 

A s srednje ploskve A s , vrednost integrala v prvem členu pa je odvisna 

od tretje potence majhne debeline stene δ in je zato zanemarljivo majhna 

v primerjavi z vrednostjo drugega člena 

3


A s = A n + A x 

2 

... 

∮ 

1 

3 

δ 3 dζ ≪ 2 ϕ n A s . (T.13) 

C s 

Torzijski vztrajnostni moment zaprtega enoceličnega tenkostenskega 

prereza lahko torej dovolj natančno izračunamo s preprosto formulo 

I x =2ϕ n A s . 

(T.14) 

Seveda pa moramo najprej določiti vrednost napetostne funkcije ϕ n na 

notranji konturi C n . V ta namen uporabimo dodatni kompatibilnostni 

pogoj (5.186) za prerez z eno notranjo odprtino, ki pa ga tokrat ob 

upoštevanju tankostenske narave nosilca zapišemo za srednjo krivuljo 

C s in glede na koordinatno bazo (e η , e ζ ) 

∮ 

C s 

∂ϕ 

∂η 

∣ dζ = −2 A s . 

η=0 

(T.15) 

Poudarili smo, da je pri integriranju po krivulji C s vseskozi η =0. Z 

odvajanjem enačbe (T.7) dobimo 

∂ϕ 

∂η = −2η − ϕ n 

δ 

→ 

∂ϕ 

∂η ∣ = − ϕ n 

η=0 

δ . 

(T.16) 

Ker je ϕ n konstanta, iz enačbe (T.15) sledi 

ϕ n 

∮ 

C s 

dζ 

δ =2A s → ϕ n = 2 A s 

∮ 

dζ 

C s 

δ 

. (T.17) 

Zvstavitvijovenačbo (T.14) dobimo tako imenovano 2. Bredtovo formulo 

za določitev torzijskega vztrajnostnega momenta zaprtega enoceličnega 

tenkostenskega prereza 

I x = 4 A2 s 

∮ 

C s 

dζ 

δ 

. (T.18) 

4


Stemlahkoobupoštevanju enačbe (5.190) določimo specifični torzijski 

zasuk θ 

θ = 

M ∮ 

x dζ 

4GA 2 s δ . 

(T.19) 

Glavni cilj naloge pa je seveda določitev napetosti. Iz druge od enačb 

(T.2) in prve od enačb (T.16) sledi 

σ xζ = M ( 

x 

2η + ϕ ) 

n 

. (T.20) 

I x δ 

Kakor vidimo, je strižna napetost σ xζ linearna funkcija koordinate η, 

ki se na območju stene prereza spreminja v mejah od −δ/2 do+δ/2. 

Največjo vrednost doseže na zunanjem, najmanjšo pa na notranjem 

robu prereza 

( 

σxζ max = σ xζ η = δ ) 

= M ( 

x ϕn 

) 

2 

δ + δ 

C s 

I x 

( 

σxζ min = σ xζ η = − δ ) 

= M x 

2 I x 

( ϕn 

δ − δ ) 

. 

(T.21) 

Pri tankostenskem prerezu je jasno, da se robni vrednosti napetosti 

le malo razlikujeta med seboj. Zato pri praktičnih nalogah dosledno 

računamo kar z enakomerno povprečnovrednostjostrižne napetosti ¯σ xζ , 

za katero običajno vpeljemo tudi preprostejšo oznako τ s (slika T-1) 

τ s =¯σ xζ = σ xζ (η =0) → τ s = M x ϕ n 

δI x 

. (T.22) 

Za torzijski vztrajnostni moment I x vstavimo izraz (T.14) in dobimo 

1. Bredtovo formulo za strižno napetost v tanki steni zaprtega enoceličnega 

prereza 

τ s = 

M x 

. (T.23) 

2 δA s 

Dobljena formula pove, da je strižna napetost v steni zaprtega prereza 

največja tam, kjer je debelina stene najmanjša. Če enačbo (T.23) 

5


pomnožimo z δ, dobimo tako imenovani strižni tok q s ,kijeenakomeren 

vzdolž celotne srednje krivulje prereza C s 

q s = δτ s = M x 

2 A s 

= konst. (T.24) 

Opazimo lahko analogijo s tokom idealne tekočine po cevi spremenljivega 

prereza, pri čemer vlogo ploščine prereza prevzame debelina 

stene δ, vlogo hitrosti pa torzijska strižna napetost τ s . 

Čistatorzijaravneganosilcazzaprtimvečceličnim tankostenskim 

prečnim prerezom 

Podobno kot pri nosilcu z enoceličnim prečnim prerezom ravnamo 

tudi pri določitvi mehanskega stanja nosilca z večceličnim zaprtim 

tankostenskim prerezom pri čisti torzijski obtežbi. Oglejmo si primer 

prečnega prereza s tremi notranjimi odprtinami (slika T-2.a). 

Sredinske črte obodne in notranjih sten tvorijo srednje krivulje C s1 , C s2 

in C s3 , ki obkrožajo srednje ploskve nad posameznimi odprtinami 

A s1 , A s2 in A s3 s ploščinami A s1 ,A s2 ,A s3 . Konstantne vrednosti 

napetostne funkcije nad konturami notranjih odprtin označimo s 

ϕ 1 ,ϕ 2 ,ϕ 3 . 

Poissonovo diferencialno enačbo čiste torzije torej rešujemo ob enakih 

predpostavkah kot v prejšnjem primeru in dobimo tudi enako splošno 

rešitev 

ϕ = −η 2 + C 1 η + C 2 . 

(T.25) 

Pri določanju integracijskih konstant C 1 in C 2 moramo tokrat upoštevati, 

da sta pri notranjih stenah obe robni vrednosti napetostne funkcije 

različni od nič (slika T-2.b) 

6 

( 

ϕ η = − δ ) 

= ϕ B 

2 

( 

ϕ η = δ ) → 

= ϕ A 

2 

⎧ 

⎪⎨ 

⎪⎩ 

C 1 = ϕ A − ϕ B 

δ 

C 2 = ϕ A + ϕ B 

2 

+ δ2 

4 

(T.26)


Slika T-2 

Rešitev Poissonove diferencialne enačbejetorej 

ϕ = −η 2 + ϕ A − ϕ B 

δ 

η + ϕ A + ϕ B 

2 

+ δ2 

4 

(T.27) 

sprvimodvodompoη 

∂ϕ 

∂η = −2η + ϕ A − ϕ B 

δ 

→ 

∂ϕ 

∂η 

∣ = ϕ A − ϕ B 

η=0 

δ 

. (T.28) 

Vrednosti napetostne funkcije nad notranjimi odprtinami ϕ 1 ,ϕ 2 ,ϕ 3 

izračunamo iz dodatnih kompatibilnostnih enačb, ki jih zapišemo vzdolž 

7


sklenjenih srednjih črt C s1 , C s2 , C s3 okrog notranjih odprtin 

∮ 

C s1 

∮ 

C s2 

∮ 

C s3 

∂ϕ 

∂η ∣ dζ = −2 A s1 

η=0 ∂ϕ 

∂η ∣ dζ = −2 A s2 

η=0 ∂ϕ 

∂η ∣ dζ = −2 A s3 . 

η=0 

(T.29) 

Nastopajoči prvi odvodi napetostne funkcije očitno niso gladke funkcije 

vzdolž srednjih krivulj. Zato srednje krivulje razdelimo na odseke, 

vzdolž katerih so integrandi gladke funkcije in krivuljne integrale po 

sklenjenih krivuljah izračunamo kot vsote integralov po posameznih 

odsekih. Začnimo s prvo od enačb (29). Na odseku od točke 1 do točke 

3jeϕ A = ϕ z =0inϕ B = ϕ 1 ,naodseku32 je ϕ A = ϕ 3 in ϕ B = ϕ 1 , 

na odseku 21 pa je ϕ A = ϕ 2 in ϕ B = ϕ 1 . Ob upoštevanju enačb (28) 

se prva od enačb (29) glasi 

∫ 3 

1 

0 − ϕ 1 

δ 

dζ + 

∫ 2 

3 

ϕ 3 − ϕ 1 

δ 

dζ + 

∫ 1 

2 

ϕ 2 − ϕ 1 

δ 

dζ = −2 A s1 . (30) 

Podobno zapišemo tudi preostali dve dodatni kompatibilnostni enačbi 

in dobimo 

∫ 1 

4 

∫ 4 

3 

0 − ϕ 2 

δ 

0 − ϕ 3 

δ 

dζ + 

dζ + 

∫ 2 

1 

∫ 2 

4 

ϕ 1 − ϕ 2 

δ 

ϕ 2 − ϕ 3 

δ 

dζ + 

dζ + 

∫ 4 

2 

∫ 3 

2 

ϕ 3 − ϕ 2 

δ 

ϕ 1 − ϕ 3 

δ 

dζ = −2 A s2 

dζ = −2 A s3 . 

(31) 

Ker so ϕ 1 ,ϕ 2 ,ϕ 3 konstantne vrednosti, po ureditvi in množenju z −1 

8


sledi 

ϕ 1 

∮ 

C s1 

−ϕ 1 

∫ 2 

1 

−ϕ 1 

∫ 3 

Zvpeljavookrajšav 

a 11 = 

∮ 

C s1 

2 

dζ 

δ 

∫ 2 

dζ 

a 21 = − 

1 δ 

∫ 3 

dζ 

a 31 = − 

2 δ 

dζ 

δ − ϕ 2 

dζ 

δ + ϕ 2 

dζ 

δ − ϕ 2 

∫ 1 

2 

∮ 

C s1 

∫ 2 

4 

dζ 

δ − ϕ 3 

dζ 

δ − ϕ 3 

dζ 

δ + ϕ 3 

∫ 1 

dζ 

a 12 = − 

2 δ 

a 22 = 

∮ 

C s2 

dζ 

δ 

∫ 2 

dζ 

a 32 = − 

4 δ 

∫ 2 

3 

∫ 4 

2 

∮ 

C s1 

dζ 

δ =2A s1 

dζ 

δ =2A s2 

dζ 

δ =2A s3 . 

∫ 2 

dζ 

a 13 = − 

3 δ 

∫ 1 

dζ 

a 24 = − 

2 δ 

a 33 = 

∮ 

C s3 

dζ 

δ 

(32) 

(33) 

ter 

b 1 =2A s1 b 2 =2A s2 b 3 =2A s3 (34) 

lahko sistem (32) zapišemo v pregledni obliki 

a 11 ϕ 1 + a 12 ϕ 2 + a 13 ϕ 3 = b 1 

a 21 ϕ 1 + a 22 ϕ 2 + a 23 ϕ 3 = b 2 

a 31 ϕ 1 + a 32 ϕ 2 + a 33 ϕ 3 = b 3 . 

Tako smo dobili sistem linearnih algebrajskih enačb, iz katerega brez 

težav določimo konstantne vrednosti napetostne funkcije ϕ 1 ,ϕ 2 in ϕ 3 . 

Dobljene ugotovitve lahko posplošimo za primer tankostenskega prereza 

z N notranjimi odprtinami. Tedaj lahko sistem kompatibilnostnih 

9


enačb na kratko zapišemo z enačbo 

N∑ 

a ij ϕ j = b i (i =1, 2, ..., N) (35) 

j=1 

ali v matrični obliki 

[a ij ] {ϕ j } = {b i } (i, j =1, 2, ..., N) . (36) 

Koeficienti a ij in desne strani b i so podani z izrazi 

∮ 

dζ 

a ii = 

δ 

C si 

∫ 

dζ 

(i ≠ j) ... a ij = − 

δ = a ji (i, j =1, 2, ... ,N) 

l ij 

b i =2A si . 

(37) 

Pri tem smo z l ij označili skupni odsek srednjih krivulj C si in C sj ,torej 

dolžino skupne stene med celicama i in j. 

Zvstavitvijorešitve za napetostno funkcijo (27) in izračunanih vrednosti 

napetostne funkcije nad notranjimi odprtinami ϕ i v splošno 

enačbo za torzijski vztrajnostni moment (5.194) bi na podoben način 

kakor pri enoceličnem prerezu dobili 

I x = 1 3 

⎛ 

⎜ 

⎝ 

∮ 

C sz 

δ 3 dζ + ∑ ∫ 

l ij 

⎞ 

δ 3 ⎟ 

dζ⎠ +2 

N∑ 

ϕ i A si . 

i=1 

(T.38) 

Prvi integral v okroglem oklepaju izvrednotimo vzdolž sklenjene srednje 

krivulje C sz obodne stene. S tem prvi člen v enačbi (38) predstavlja 

prispevek obodne in notranjih sten kot odprtih ozkih profilov k torzijskemu 

vztrajnostnemu momentu prereza. Vendar lahko z enakim 

razmislekom kakor sicer pri tankostenskih zaprtih prerezih prvi člen v 

10


izrazu za I x zanemarimo v primerjavi z drugim in v praktičnih nalogah 

računamo s poenostavljeno formulo 

I x =2 

N∑ 

ϕ i A si . 

i=1 

(T.39) 

Končno določimo še strižne napetosti. Iz druge od enačb (T.2) in prve 

od enačb (T.28) sledi 

σ xζ = M ( 

x 

2η − ϕ ) 

A − ϕ B 

. (T.40) 

I x δ 

Vpraktičnih nalogah je pri tankostenskih zaprtih prerezih umestno 

računati kar s povprečno vrednostjo strižne napetosti τ s 

τ s =¯σ xζ = σ xζ (η =0) → τ s = M x 

δI x 

(ϕ B − ϕ A ) . 

(T.41) 

Za dimenzioniranje oziroma kontrolo torzijske nosilnosti prereza je praviloma 

merodajna največja vrednost strižne napetosti τ s . Da bi ugotovili, 

kolikšna je ta napetost in kje nastopa, moramo vzdolž vsehsrednjih 

krivulj izvrednotiti razmerje med razliko napetostnih funkcij na 

robovih ϕ B − ϕ A in debelino stene δ. 

11

Čista torzija ravnega nosilca z zaprtim enoceličnim ... - FGG-KM

Create successful ePaper yourself

Delete template?

Save as template?