1 ZADANIA NA ĆWICZENIA 3 I 4 Zadanie 1. Wygeneruj szkody dla ...

Agata Boratyńska Statystyka aktuarialna . . . 1
ZADANIA NA ĆWICZENIA 3 I 4
Zadanie 1.
Wygeneruj szkody dla polis z kolejnych lat wg rozkładu P (N = 1) = 0, 1 P (N = 0) = 0, 9,
gdzie N jest liczbą szkód z jednej polisy. Wygeneruj wartości X szkód wg rozkładu
P (X = 100) = 0, 5, P (X = 200) = 0, 25, P (X = 500) = 0, 25. Szkody o wartości
500 są regulowane w roku następnym szkody o pozostałych wartościach w roku zajścia.
Wylicz składki na każdy rok w następujący sposób:
składka I: w latach 1980-1981 składka po 25, w latach następnych składka=średnia ze
szkód wypłaconych w roku poprzednim razy częstość szkód w roku poprzednim razy 1,1
składka II: w latach 1980-1981 składka po 25, w latach następnych - w roku n - składka=średnia
ze szkód zaistniałych w roku n − 2 razy częstość szkód w roku n − 2 razy
1,1
Którą z metod uważasz za rozsądniejszą i dlaczego.
Uwaga: Średnia ze szkód i częstość szkód jest liczona na podstawie symulacji.
Wyniki przedstaw w tabelach. Wyznacz też składki nie opierając się na symulacjach ale
na parametrach odpowiednich rozkładów. Porównaj wyniki.
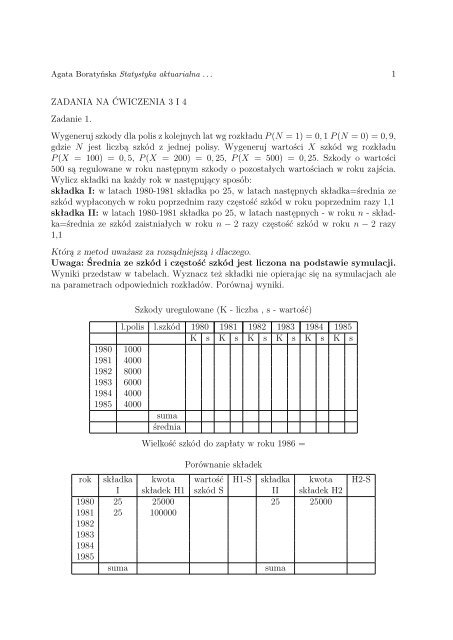
Szkody uregulowane (K - liczba , s - wartość)
l.polis l.szkód 1980 1981 1982 1983 1984 1985
K s K s K s K s K s K s
1980 1000
1981 4000
1982 8000
1983 6000
1984 4000
1985 4000
suma
średnia
Wielkość szkód do zapłaty w roku 1986 =
Porównanie składek
rok składka kwota wartość H1-S składka kwota H2-S
I składek H1 szkód S II składek H2
1980 25 25000 25 25000
1981 25 100000
1982
1983
1984
1985
suma
suma

Agata Boratyńska Statystyka aktuarialna . . . 2
Zadanie 2. (egzaminy aktuarialne) Portfel składa się z n = 1000 niezależnych jednorodnych
ryzyk. Dla pojedynczego ryzyka wartość oczekiwana roszczeń jest równa 10 i odchylenie
standardowe też jest równe 10. Niech S oznacza sumaryczną wartość roszczeń w portfelu.
Składka przypadająca na pojedyncze ryzyko wynosi H i została skalkulowana tak aby
P (S > nH) = 0, 01,
przy czym to prawdopodobieństwo obliczono korzystając z aproksymacji rozkładem normalnym.
Przypuśćmy, że możemy objąć ubezpieczniem dodatkowych n 1 niezależnych ryzyk, dla
których wartość oczekiwana roszczeń jest równa 10 ale odchylenie standardowe jest równe
15. Dla nowych ryzyk składka powinna być tej samej wysokości H. Niech S 1 oznacza
sumaryczną wartość roszczeń w portfelu nowych ryzyk. Wyznacz n 1 aby
P (S + S 1 > (n + n 1 )H) 0, 01.
Zadanie 3. (egzaminy aktuarialne) Ubezpieczyciel ma portfel liczący 9644 terminowych
polis na życie z terminem jednego roku. Prawdopodobieństwo zgonu każdego z ubezpieczonych
wynosi 0,01, a świadczenie wynosi b. Ubezpieczyciel pobiera składkę w wysokości
125% składki netto. Reasekurator w zamian za zobowiązanie pokrycia ab w razie śmierci
ubezpieczonego żąda 150% swojego udziału w składce netto. Ubezpieczyciel chce utrzymać
prawdopodobieństwo straty na udziale własnym w tym portfelu na poziomie 0,05.
Nie ma kosztów, stopa procentowa jest zerowa. Wyznacz wskaźnik a ∈ [0, 1]. Zastosuj
aproksymację rozkładem normalnym.
Zadanie 4. Rozważmy następujący portfel ubezpieczeń życiowych.
k nr grupy n k - liczba ryzyk b k - świadczenie
1 8000 1
2 3500 2
3 2500 3
4 1500 5
5 500 10
Prawdopodobieństwo zgonu we wszystkich grupach jest jednakowe i wynosi 0,02. Towarzystwo
ubezpieczeniowe zastanawia się nad reasekuracją z poziomem retencji r przy koszcie
jednostki pokrycia c.
a) Dysponując kapitałem ze składek w wysokości 825 oszacuj prawdopodobieństwo, że
łączna wartość wypłat i kosztów reasekuracji przekroczy tę kwotę, przy założeniu, że
r = 2 i c = 0, 025.
b) Dobierz r ∈ [3, 5), tak aby prawdopodobieństwo zdarzenia z punktu a było najmniejsze.

Agata Boratyńska Statystyka aktuarialna . . . 3
Zadanie 5. Portfel składa się z 2 niezależnych subportfeli. Wyznaczono charakterystyki
łącznej wartości szkód dla tych subportfeli. Przedstawia je tabela.
Wartość oczekiwana wariancja skośność γ
subportfel I 5 9 2
subpotrfel II 15 16 0,25
Rozkład łącznej wartości szkód z całego portfela aproksymujemy przesuniętym rozkładem
gamma, zakładając, że trzy pierwsze momenty obu rozkładów są równe. Wyznacz
parametry rozkładu gamma.
Zadanie 6. Rozważmy trzy grupy ryzyka
k n k - liczba q k - p-stwo
polis w k-tej grupie szkody
1 100 0.1
2 150 0.2
3 200 0.08
Wartość szkody jest równa 2. Wyznacz składkę łączną H w każdej grupie osobno i łącząc
grupy po dwie według zasady P (S > H) = 0, 02 stosując aproksymację rozkładem
normalnym i rozkładem gamma.
Zadanie 7. Wygeneruj 1000 polis wg modelu indywidualnego z prawdopodobieństwem
szkody q = 0, 2 i wartością szkody a) Y ∼ Ex(0, 01) b) Y ∼ P areto(5, 400). Na podstawie
otrzymanych danych oszacuj odpowiednie parametry rozkładu liczby i wartości szkód, a
następnie korzystając z tych estymatorów oszacuj składkę łączną H, dla portfela złożonego
z 1000 polis tego samego typu, tak, by P (S > H) = 0, 05, gdzie S suma szkód. Zastosuj
aproksymację rozkładem normalnym i gamma. Wylicz też H wykorzystując rzeczywiste
parametry rozkładu, a nie wartości estymatorów otrzymanych na podstawie próby losowej.
Przeprowadź 100000 symulacji portfela złożonego z 1000 polis o parametrech ryzyka jak
na początku treści zadania, dla każdej symulacji oblicz sumę szkód i traktując otrzymane
wyniki jako próbke rozkładu zmiennej S wyznacz oszacowanie składki jako odpowidni
kwantyl próbkowy. Porównaj wyniki z wcześniej otrzmanymi oszacowaniami.
Zadanie 8. Dla pewnego portfela ryzyk liczba szkód ma rozkład Poissona z wartością
oczekiwaną 10, wysokość pojedynczej szkody jest zmienną o rozkładzie Ex(1/200). Ubezpieczyciel
pokrywa nadwyżkę szkody ponad 100. Podaj wartość oczekiwaną, wariancję i
współczynnik asymetrii γ sumy wypłaconych odszkodowań.
Zadanie 9. Liczba szkód N z ryzyka ma rozkład geometryczny
P (N = k) = p(1 − p) k dla k = 0, 1, 2, . . .

Agata Boratyńska Statystyka aktuarialna . . . 4
Wartość pojedynczej szkody X i ma rozkład wykładniczy o wartości oczekiwanej 1/θ.
Wyznacz dystrybuantę, gęstość i funkcję tworzącą momenty rozkładu zmiennej
S N =
{ ∑Ni=1
X i gdy N > 0
0 w p.p.
Zadanie 10. Rozważmy trzy grupy ryzyka, liczba szkód dla każdego ryzyka jest zmienną
o rozkładzie Poissona (parametry podaje tabela).
k n k - liczba λ k - oczekiwana
polis w k-tej grupie liczba szkód
1 100 0.1
2 150 0.2
3 200 0.08
Wartość szkody jest równa 2. Wyznacz składkę łączną H w każdej grupie osobno i łącząc
grupy po dwie według zasady P (S > H) = 0, 02 stosując aproksymację rozkładem
normalnym i rozkładem gamma. Porównaj wyniki z wynikami zadania 6.
Zadanie 11. Rozważamy portfel ryzyk
k n k - liczba q k - p-stwo b k
polis w k-tej grupie roszczenia - wartość
1 1000 0.004 10000
2 1500 0.0035 20000
3 2500 0.003 100000
TU chce zawrzeć kontrakt reasekuracyjny o współczynniku retencji M w przedziale
(20000, 100000) za składkę równą 130% oczekiwanego kosztu pokrytych szkód przez reasekuratora.
Niech S(M) oznacza odszkodowania pokryte przez ubezpieczyciela przy limicie
reasekuracji M. Podaj parametry złożonego rozkładu Poissona jako aproksymacji dla
zmiennej S(M). Stosując aproksymację złożonym rozkładem Poissona wyznacz ES(M)
i V arS(M). Wyznacz M, przy którym prawdopodobieństwo zdarzenia, że S(M) plus
opłata za reasekurację przekroczą poziom 1135000 jest najmniejsze (zastosuj do złożonego
rozkładu Poissona aproksymację rozkładem normalnym).