PR ¨UFUNG TM I,II UND ETM I,II - Lehrstuhl für Technische Mechanik

1. Aufgabe: (TM, ETM)
2l
ERGEBNISSE
PRÜFUNG TM I,II UND ETM I,II
Lehrstuhl für Technische Mechanik, TU Kaiserslautern
x1
A
WS 07/08, 23.02.2008
3
2 l
α
B
F (Feldmitte)
x2
2l
q0
000 111
000 111
000 111
000 111
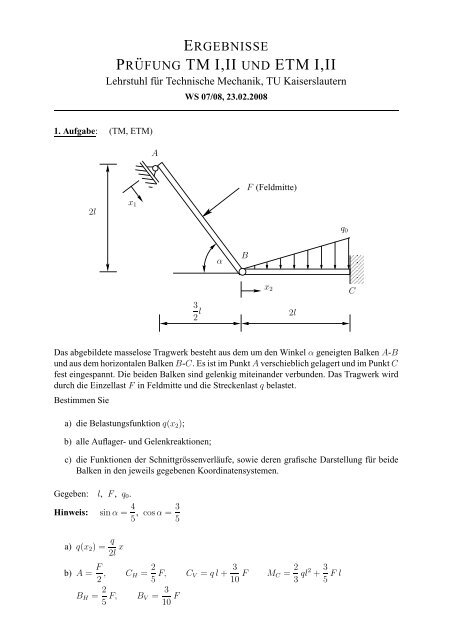
Das abgebildete masselose Tragwerk besteht aus dem um den Winkelαgeneigten Balken A-B
und aus dem horizontalen BalkenB-C. Es ist im PunktAverschieblich gelagert und im PunktC
fest eingespannt. Die beiden Balken sind gelenkig miteinander verbunden. Das Tragwerk wird
durch die EinzellastF in Feldmitte und die Streckenlast q belastet.
Bestimmen Sie
a) die Belastungsfunktionq(x2);
b) alle Auflager- und Gelenkreaktionen;
c) die Funktionen der Schnittgrössenverläufe, sowie deren grafische Darstellung für beide
Balken in den jeweils gegebenen Koordinatensystemen.
Gegeben: l, F , q0.
Hinweis: sinα = 4 3
, cosα =
5 5
a) q(x2) = q
2l x
b) A = F
2 , CH = 2
5 F, CV = ql+ 3
10 F MC = 2
3 ql2 + 3
F l
5
BH = 2
5 F, BV = 3
10 F
C

c)
0 ≤ x1 ≤ 5
4 l
0 ≤ x1 ≤ 5
2 l
0 ≤ x2 ≤ 2l
x1
x1
BH
N(x)
Q(x)
M(x)
A
A
BV
x2
F
2
0
Q
+
+
N
Q
F
M
N
Q
N
M
M
− F
2 − 3
10 F
5
8 Fl
+
quadratisch
kubisch
N(x1) = 0
Q(x1) = F
2
M(x1) = F
2 x1
N(x1) = 0
Q(x1) = − F
M(x1) = F
N(x2) = 2
5 F
2
5 x1
l−
4 2
Q(x2) = − 3 q
F −
10 4l x22 M(x2) = − 3
10 Fx2 − q
12l x32 2
5F − 3
F −ql 10
3 2
Fl− 5 3 ql2

2. Aufgabe: (TM, ETM)
a
2
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
µ2
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111 µ1
00000000000000
11111111111111
r
00000000000000
11111111111111
F
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111 α
0000000000000000000
1111111111111111111 00000000000000
11111111111111
0000000000000000000
1111111111111111111 00000000000000
11111111111111
0000000000000000000
1111111111111111111 00000000000000
11111111111111
0000000000000000000
1111111111111111111
µ1
a
2
b
Ein masseloser Keil wird mit der Kraft F unter eine massebehaftete Scheibe mit der Masse m
geschoben. Zwischen dem Keil und der Unterlage und zwischen der Scheibe und der Wand
wirkt der Reibungskoeffizientµ1, zwischen Keil und Scheibe der Reibungskoeffizientµ2.
Bestimmen Sie
a) den Schwerpunkt der Scheibe im angegebenen Koordinatensystem;
b) die Mindestgröße der Kraft F für den Fall, dass der Keil gerade nicht herausrutscht.
Gegeben: a = 6cm; b = 2cm; r = 5
2 √ π cm;
m; α = 30◦ ; µ1 = 1
10 ; µ2 = 1
5
a) xs = 4 47
143 cm ys = 3 61
143 cm
b) F = −G cosα−µ1sinα
1−µ1µ2
y
b
(µ1µ2 −1)sinα+(µ1 +µ2)cosα = 0,192G
a
2
a
2
x

3. Aufgabe: (TM)
l
2
l
l
2
l
F
l
2
2F
3
2 l
A G
B
M
C D
H
Das dargestellte System besteht aus vier masselosen starren Balken. Es ist wie angegeben durch
zwei EinzellastenF und2F , ein EinzelmomentM und eine konstante Streckenlast q belastet.
Berechnen Sie mit dem Prinzip der virtuellen Verschiebungen
a) Die horizontale Auflagerkraft inA;
b) Die vertikale Auflagerkraft inA;
Gegeben: F, q, M, l
Anmerkung: Sämtliche Polpläne, Verschiebungsbilder sowie kinematischen Beziehungen sind
anzugeben.
Eine Lösung der Aufgabe mit Gleichgewichtsbedingungen wird nicht bewertet.
a) AH = 4
3 F
b) AV = 4
5
F + 3
5
3M
ql −
5 l
2l
q

4. Aufgabe: (TM, ETM)
l
l
q0
D
qz
s1
C
3l
B
l
A
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
000000000
111111111
Das dargestellte masselose System besteht aus einem Ausleger mit kreisrundem Querschnitt
(Radius R, ElastizitätsmodulE, Schubmodul G) und einem starrem Hebel. Der Hebel und der
Ausleger sind inC rechtwinklig fest miteinander verschweißt.
Der Ausleger ist in A fest eingespannt, über den Hebel wird eine lineare Streckenlast qz(y) in
das System eingebracht.
Das Tragwerk liegt in derx,y-Ebene.
Bestimmen Sie
a) die Schnittgrößen im Ausleger in Abhängigkeit der angegebenen Koordinates1,
b) die Durchbiegung im PunktC,
c) die Verdrehung des Auslegers im Punkt C,
d) die Absenkung an der StelleDund
e) den Spannungstensor im PunktB (s1 = 2l, z = R).
Gegeben: E, G, l, q0, R = l/20.
2 q0l
a) Nx(s1) = 0 Qz(s1) = lq0 Mx =
3
b) w(C) = − 576·104 q0
Eπ
= −1.8346·10 6q0
E
c) ϕ(C) = 32·104 q0
= 1.10859·105
Gπl2 Gl2 d) Zwei Anteile:
• Absenkung inC
• Anteil aus Torsion: −ltan(ϕ) ≈ −lϕ
w(D) = − 576·104 q0
Eπ
− 32·104 q0
Gπl
My(s1) = −lq0s1
x
z
y

e) Klare Null-Anteile
• Anteil aus NormalkraftσNx = 0, daNx(s1) = 0,
• Anteileσy = τyz = 0, keine Belastung in y-Richtung,
• Anteileσz = 0, keine Lasten in z-Richtung entlang Balkenachse.
Normalspannung aus Biegung:
σx(s1) = M(s1)
z daher
Iy
σx(B) = −8l2 q0R
πR 2
und
Schubspannung aus Torsion:
τp(r) = Mx
r =
It
4q0
3πl2 τp(r) = τxy.
Schubspannung aus Querkraft:
τxz = 0

5. Aufgabe: (TM)
Qy
e
s1
y
l
Dargestellt ist der Querschnitt eines symmetrischen dünnwandigen Profils mit konstanter Wanddicke
t. Das Profil ist durch die Querkraft Qy belastet, deren Wirkungslinie gegenüber der
y-Achse um den Betrag e verschoben ist.
a) Bestimmen Sie die Lage des Schwerpunkts S, d.h. bestimmen Sie den Abstand a zum
Profil.
b) Bestimmen Sie das FlächenträgheitsmomentIzz.
c) Bestimmen Sie die SchubspannungenτQ infolge der Querkraft Qy.
d) Bestimmen Sie die Lage der maximalen Schubspannungenτ max
Q infolge der QuerkraftQy.
e) Wie groß darf die Exentrizitäte maximal sein, so dass die maximale Schubspannung den
Betrag 10 N/cm 2 nicht übersteigt?
Für diesen Aufgabenteil gelten die folgenden Annahmen:
l = 10 cm, t = 1 cm, Q = 50 N, α = 60.
Gegeben: l, Q, α = 60
a) zS = 0 aus Symmetrie, a = 0,125l
b) Izz = 5
48 l3 t
a
α
S
z
l

c) Schubfluss infolge Querkraft
τ = QyS(y)
Izzt
SI(y) = ydA =
ytds1 = 1
4 s2 3
1t− 8 ls1t
day = s1cos60− 3
8 l und s1 läuft von 0 bis l.
SII(y) = 1
4 l2t− 3
8 l2
t+ ytds2
= 1
4 l2t− 3
8 l2t+ 1
8 ls2t
day = 1/8l und s2 läuft von 0 bis l.
Daraus folgt für die maximalen Schubspannungen:
Si(y) ′ = 1/2s1 −3/8l = 0 ⇒ s1 = 3/4l
d) exzentrische Querkraft ⇒ TorsionsmomentMT = −Qe
τM = MT
t IT = 4/3lt
IT
3
Berechnung vone:
τmax Q +τmax
Qy
M =
Izzt
e ≤ 0.866667
τM = 3Qet
4lt 3
− 1 9
416
l2t+ 33
84
l2
t
+ 3Qet
≤ k
4lt2

6. Aufgabe: (ETM, TMII)
A
EA
R
C
Das dargestellte Tragwerk besteht aus einem Bogenträger mit der BiegesteifigkeitEI und einem
gelenkig verbundenen Stab mit der Dehnsteifigkeit EA. Der Stab ist in den Punkten A und C
gelenkig mit dem Bogenträger verbunden. Im PunktB wirkt eine horizontale Kraft F .
Bestimmen Sie
a) alle Auflagerkräfte,
b) die Stabkraft,
c) die horizontale Verschiebung des PunktesB,
d) für den Sonderfall eines dehnstarren Stabes (d.h. EA → ∞) und eines sehr weichen
Stabes (d.h. EA → 0) die Verschiebung des PunktesB.
Gegeben: R, F , EA, EI
Anmerkung:
Im Bogenträger sind nur Energieanteile infolge des Biegemoments zu berücksichtigen. Der
Aufgabenteil d) kann auch ohne b) und c) gelöst werden.
Hinweis:
2 1 1
sin (x)dx = x−
2 4 sin(2x)
R
EI
B
F

a) Ax = −F, Ay = 0, B = 0
b) S = R2 πA
R 2 πA+4I F
c) uB = R3 πF
E
1
2I +
2
R2
πA+4I
d) EA → 0 uB = R3 πF
EI
EA → ∞ uB = R3 πF
2EI

7. Aufgabe: (ETM)
l
ω1
y
B
A
α
Das dargestellte System besteht aus einem im Punkt A drehbar gelagerten Schwungrad und
zwei Kurbeln. Die Kurbel B-C verbindet das Schwungrad mit der Kurbel C-D, dabei ist die
KurbelC-D im PunktD drehbar gelagert. Das Schwungrad dreht sich mit der konstanten Winkelgeschwindigkeitω1.
a) Zeichnen Sie die Richtung der Geschwindigkeiten VB und VC, sowie die Lage des Momentanpols
der StangeB-C.
b) Berechnen Sie die momentane Winkelgeschwindigkeiten der zwei Kurbeln ωBC = ω2
und ωDC = ω3.
c) Berechnen Sie die momentane Winkelbeschleunigungen der zwei Kurbeln ˙ωBC = ˙ω2 und
˙ωDC = ˙ω3.
Gegeben: l, ω1, α = 30 ◦ , β = 60 ◦ .
2l
C
β
D
3
2 l
x

a)
vB
M b) vB =
vC
⎡
0
c) von A aus aB = ⎣−ω2
⎤
1 l⎦
0
⎡ ⎤
−ω1l
⎢ ⎥
⎣ 0 ⎦
0
⎡ ⎤ ⎡
−ω1l
⎢ ⎥ ⎢
vC = ⎣ 0 ⎦+ ⎣
0
ω2
⎡
3
−ω3 ⎢
vC = ⎢
⎣
√ 3
l
4
3
−ω3
4 l
⎤
⎥
⎦
0
ω2 l
√ 3l
0
⎤
√
3
ω2 = −
4 ω3 ω3 = 2
√ ω1
3
ω2 = − 1
2 ω1
⎡
0
von B aus aC = ⎣−ω2
⎤ ⎡ ⎤ ⎡
√
˙ω2l
1 l⎦+
⎣ 3 ˙ω2 l⎦+
⎣
0 0
−ω2 √ ⎤
2 3 l
⎦
von D aus
⎡
3
⎢−˙ω3
⎢
aC = ⎢
⎣
√ 3
l
4
3
−˙ω3
4 l
⎤
⎥
⎦
0
+
⎡
⎢
⎣
˙ω3 = 4 √ ω
3 2 1 ˙ω2 = ω 2 √
3
1 −2−
4
−ω 2 3
3
˙ω3
4 l
3 √ ⎤
⎥
3 ⎥
l
⎥
4
⎦
0
ω 2 2 l
0
⎥
⎦ vonB aus
vonD aus

8. Aufgabe: (ETM I)
g
m1
ϕ2
x1
a
m2, Θ2
x3
ϕ3
r
R
m3, Θ3
Die Masse m1 ist mit einem Seil, das über eine Walze(Massenträgheitsmoment bezüglich des
SchwerpunktesΘ2, Massem2) und eine masselose Rolle umgelenkt wird, mit einer Rolle (Massenträgheitsmoment
bezüglich des Schwerpunktes Θ3, Masse m3) verbunden. Das System befindet
sich zunächst in Ruhe und rollt im weiteren ohne zu gleiten.
a) Schneiden Sie das System vollständig frei und stellen Sie die kinematischen Beziehungen
auf. Verwenden Sie die eingezeichneten Koordinaten.
b) Bestimmen Sie die Beschleunigung ¨x1 der Masse m1 and die Beschleunigung ¨x3 der
Massem3.
c) Bestimmen Sie die Schwerpunktsgeschwindigkeit v3 der Rolle, wenn die Masse m1 die
Strecke x1 = h zurückgelegt hat.
Gegeben: g, a, r, R = 2r
m, m1 = m3 = m, m2 = 4m
Θ2 = m2
2 a2 , Θ3 = m3
2 R2

a)
m 1 g
S 1
x1
↓ : m1¨x1 = m1g −S1
B : Θ2¨ϕ2 = S1a−S2a
← : m3 ¨x3 = S2 −R3
C : Θ3¨ϕ3 = −S2r +R3R
Kinematik: ¨x1 = a¨ϕ2 ¨x1 = r¨ϕ3 ¨x3 = 2¨ϕ3
b) ¨x1 = 1
9 g ¨x3 = 2
9 g
c) v3 = 2
2gh
3
S
1
ϕ
B
2
a
m2, Θ2 S
2
S 2
x 3
ϕ
r
N R
3
3
m3, Θ3 R
3