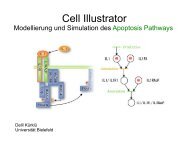
(1/4) :*: c' (1/4) - Technische Fakultät - Universität Bielefeld

Algorithmen und Datenstrukturen I
phrase1
phrase2
=
c’
e’
c’
e’
c’ (1/4)
(1/4)
(1/4)
(1/4)
(1/4) :*:
:*:
:*:
:*:
:*: d’
f’
d’
f’
d’ (1/4)
(1/4)
(1/4)
(1/4)
(1/4) :*:
:*:
:*:
:*:
:*: e’
g’
e’
g’
e’ (1/4)
(1/2)
(1/4)
(1/2)
(1/4) :*: c’ (1/4)
phrase3 = g’
e’
g’
e’
g’ (1/8)
(1/4)
(1/8)
(1/4)
:*:
:*:
:*:
:*:
a’
f’
a’
f’
(1/8)
(1/4)
(1/8)
(1/4)
:*:
:*:
:*:
:*:
g’
g’
g’
g’
(1/8)
(1/2)
(1/8)
(1/2)
:*:
g’
e’
g’
e’
(1/8)
(1/4)
(1/8)
(1/4)
e’ (1/4)
:*:
:*:
:*:
:*:
a’
:*:
a’
f’
a’
f’
(1/8)
(1/4)
(1/8)
(1/4)
c’ (1/4)
:*:
:*:
:*:
:*:
g’
g’
g’
g’
(1/8)
(1/2)
(1/8)
(1/2)
:*:
g’
e’
g’
(1/4)
(1/8)
(1/4)
(1/8)
:*:
e’ (1/4)
:*:
:*:
:*:
f’
:*:
a’
f’
a’
(1/4)
(1/8)
(1/4)
(1/8)
:*: g’ (1/2)
c’ (1/4)
:*:
:*:
:*: g’
g’
g’ (1/8)
(1/2)
(1/8) :*: f’ (1/8)
phrase4 = c’
:*:
(1/8) :*: a’ (1/8) :*: g’ (1/8) :*: f’ (1/8)
c’
:*:
g’
:*:
g’ (1/8)
(1/4)
e’ (1/4)
:*:
:*: (transponiere
:*:
(transponiere
:*:
a’
:*:
a’ (1/8)
c’ (1/4)
:*: g’ (1/8) :*: f’ (1/8)
c’
:*:
g’ (1/8)
(1/4)
e’ (1/4)
:*: a’
:*: (transponiere
:*:
a’ (1/8)
c’ (1/4)
:*: g’ (1/8) :*: f’ (1/8)
strophe
phrase4
strophe
phrase4
= wdh
c’
wdh
c’ (1/4)
phrase1
:*:
:*:
(transponiere
wdh phrase2
(-12)
:*: wdh
(g’
phrase3
(1/4)))
:*:
:*:
wdh
c’’
phr
(1
endlos
strophe
endlos
strophe
= wdh phrase1 :*: wdh phrase2 :*: wdh phrase3 :*: wdh phr
phrase1 c’ (1/4) :*: d’ (1/4) :*: e’ (1/4) :*: c’ (1/4)
ad_infinitum
wdh phrase1 :*:
strophe
wdh phrase2 :*: wdh phrase3 :*: wdh phr
bruderJakob
endlos
bruderJakob
endlos
wdh phrase1 :*: wdh phrase2 :*: wdh phrase3 :*: wdh phr
= Tempo
ad_infinitum
Tempo
ad_infinitum
wdh
ad_infinitum
wdh phrase1 :*:
andante
strophe
wdh phrase2 :*: wdh phrase3 :*: wdh phr
Tempo
ad_infinitum
wdh phrase1 :*:
andante
strophe
wdh phrase2 :*: wdh phrase3 :*: wdh phr
Tempo
(
Tempo
ad_infinitum
Tempo
ad_infinitum
andante
strophe
(
Tempo
ad_infinitum
Tempo
ad_infinitum
Tempo
ad_infinitum
Tempo
ad_infinitum
Tempo andante
strophe
einsatz
andante
strophe
einsatz
andante
strophe
(0/1)
(Instr
endlos
VoiceAahs
(einsatz
(
(einsatz
(
Tempo
(
Tempo andante (Instr VoiceAahs
(einsatz
(
Tempo
einsatz
andante
(0/1)
(Instr VoiceAahs
(einsatz
einsatz
andante
(0/1)
(Instr
(2/1)
endlos
VoiceAahs
(einsatz
einsatz
andante
(0/1)
(Instr
(2/1)
endlos
VoiceAahs
(einsatz (2/1) (transponiere 12 endlos))
:+:
(einsatz
(einsatz
(4/1)
(2/1)
endlos)
(transponiere 12 endlos)) :+:
(einsatz
(einsatz
(einsatz
(einsatz
(einsatz
(einsatz
(einsatz
(6/1)
(4/1)
(6/1)
(4/1)
(2/1)
(4/1)
(2/1)
endlos
endlos)
endlos
endlos)
(transponiere
endlos)
(transponiere 12 endlos))
(einsatz
(einsatz
(einsatz
(6/1)
(4/1)
(2/1)
endlos
endlos)
(transponiere 12 endlos))
(einsatz (6/1) endlos )))
:+:
Robert Giegerich · Ralf Hinze · Universität Bielefeld

A&D interaktiv
Universität Bielefeld
Technische Fakultät
WS 2003/2004

Inhaltsverzeichnis
1. Einleitung 1
1.1. Rechnen und rechnen lassen . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2. Die Aufgabengebiete der Informatik . . . . . . . . . . . . . . . . . . . . . 3
1.3. Einordnung der Informatik in die Familie der Wissenschaften . . . . . . . 5
2. Modellierung 7
2.1. Eine Formelsprache für Musik . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2. Typen als Hilfsmittel der Modellierung . . . . . . . . . . . . . . . . . . . . 11
2.3. Die Rolle der Abstraktion in der Modellierung . . . . . . . . . . . . . . . . 13
2.4. Modellierung in der molekularen Genetik . . . . . . . . . . . . . . . . . . 14
2.5. Anforderungen an Programmiersprachen . . . . . . . . . . . . . . . . . . . 23
3. Eine einfache Programmiersprache 25
3.1. Datentypen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.1.1. Datentypdefinitionen . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.1.2. Typsynonyme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.1.3. Typdeklarationen, Typprüfung und Typinferenz . . . . . . . . . . . 30
3.1.4. Typklassen und Typkontexte . . . . . . . . . . . . . . . . . . . . . . 32
3.2. Wertdefinitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
3.2.1. Muster- und Funktionsbindungen . . . . . . . . . . . . . . . . . . . 34
3.2.2. Bewachte Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . 36
3.2.3. Gleichungen mit lokalen Definitionen . . . . . . . . . . . . . . . . 37
3.2.4. Das Rechnen mit Gleichungen . . . . . . . . . . . . . . . . . . . . . 40
3.2.5. Vollständige und disjunkte Muster . . . . . . . . . . . . . . . . . . 41
3.3. Ausdrücke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.3.1. Variablen, Funktionsanwendungen und Konstruktoren . . . . . . . 43
3.3.2. Fallunterscheidungen . . . . . . . . . . . . . . . . . . . . . . . . . . 44
3.3.3. Funktionsausdrücke . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3.3.4. Lokale Definitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
3.4. Anwendung: Binärbäume . . . . . . . . . . . . . . . . . . . . . . . . . . . 49

ii Inhaltsverzeichnis
3.5. Vertiefung: Rechnen in Haskell . . . . . . . . . . . . . . . . . . . . . . . . 53
3.5.1. Eine Kernsprache/Syntaktischer Zucker . . . . . . . . . . . . . . . . 53
3.5.2. Auswertung von Fallunterscheidungen . . . . . . . . . . . . . . . . 53
3.5.3. Auswertung von Funktionsanwendungen . . . . . . . . . . . . . . 54
3.5.4. Auswertung von lokalen Definitionen . . . . . . . . . . . . . . . . . 56
4. Programmiermethodik 59
4.1. Spezifikation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.2. Strukturelle Rekursion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
4.2.1. Strukturelle Rekursion auf Listen . . . . . . . . . . . . . . . . . . . 62
4.2.2. Strukturelle Rekursion auf Bäumen . . . . . . . . . . . . . . . . . . 66
4.2.3. Das allgemeine Rekursionsschema . . . . . . . . . . . . . . . . . . 67
4.2.4. Verstärkung der Rekursion . . . . . . . . . . . . . . . . . . . . . . . 67
4.3. Strukturelle Induktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
4.3.1. Strukturelle Induktion auf Listen . . . . . . . . . . . . . . . . . . . 69
4.3.2. Strukturelle Induktion auf Bäumen . . . . . . . . . . . . . . . . . . 72
4.3.3. Das allgemeine Induktionsschema . . . . . . . . . . . . . . . . . . 73
4.3.4. Verstärkung der Induktion . . . . . . . . . . . . . . . . . . . . . . . 74
4.3.5. Referential transparency . . . . . . . . . . . . . . . . . . . . . . . . 76
4.4. Anwendung: Sortieren durch Fusionieren . . . . . . . . . . . . . . . . . . 76
4.4.1. Phase 2: Sortieren eines Binärbaums . . . . . . . . . . . . . . . . . 76
4.4.2. Phase 1: Konstruktion von Braun-Bäumen . . . . . . . . . . . . . . 78
4.5. Wohlfundierte Rekursion . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
4.5.1. Das Schema der wohlfundierten Rekursion . . . . . . . . . . . . . . 80
4.6. Vertiefung: Wohlfundierte Induktion . . . . . . . . . . . . . . . . . . . . . 82
5. Effizienz und Komplexität 85
5.1. Grundlagen der Effizienzanalyse . . . . . . . . . . . . . . . . . . . . . . . . 85
5.1.1. Maßeinheiten für Zeit und Raum beim Rechnen . . . . . . . . . . . 85
5.1.2. Detaillierte Analyse von insertionSort . . . . . . . . . . . . . . 86
5.1.3. Asymptotische Zeit- und Platzeffizienz . . . . . . . . . . . . . . . . 89
5.2. Effizienz strukturell rekursiver Funktionen . . . . . . . . . . . . . . . . . . 92
5.3. Effizienz wohlfundiert rekursiver Funktionen . . . . . . . . . . . . . . . . . 97
5.4. Problemkomplexität . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
5.5. Anwendung: Optimierung von Programmen am Beispiel mergeSort . . . 101
5.5.1. Varianten der Teile-Phase . . . . . . . . . . . . . . . . . . . . . . . 102
5.5.2. Berücksichtigung von Läufen . . . . . . . . . . . . . . . . . . . . . 106
5.6. Datenstrukturen mit konstantem Zugriff: Felder . . . . . . . . . . . . . . . 107
5.7. Anwendung: Ein lineares Sortierverfahren . . . . . . . . . . . . . . . . . . 112
5.8. Vertiefung: Rolle der Auswertungsreihenfolge . . . . . . . . . . . . . . . . 115

Inhaltsverzeichnis iii
6. Abstraktion 117
6.1. Listenbeschreibungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
6.2. Funktionen höherer Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . 121
6.2.1. Funktionen als Parameter . . . . . . . . . . . . . . . . . . . . . . . 121
6.2.2. Rekursionsschemata . . . . . . . . . . . . . . . . . . . . . . . . . . 125
6.2.3. foldr und Kolleginnen . . . . . . . . . . . . . . . . . . . . . . . . 128
6.2.4. map und Kolleginnen . . . . . . . . . . . . . . . . . . . . . . . . . . 133
6.3. Typklassen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
6.3.1. Typpolymorphismus und Typklassen . . . . . . . . . . . . . . . . . 137
6.3.2. class- und instance-Deklarationen . . . . . . . . . . . . . . . . 140
6.3.3. Die Typklassen Eq und Ord . . . . . . . . . . . . . . . . . . . . . . 141
6.3.4. Die Typklassen Show und Read . . . . . . . . . . . . . . . . . . . . 143
6.3.5. Die Typklasse Num . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
6.4. Anwendung: Sequenzen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
6.4.1. Klassendefinition . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
6.4.2. Einfache Instanzen . . . . . . . . . . . . . . . . . . . . . . . . . . . 150
6.4.3. Generische Instanzen . . . . . . . . . . . . . . . . . . . . . . . . . . 152
6.4.4. Schlangen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152
6.4.5. Konkatenierbare Listen . . . . . . . . . . . . . . . . . . . . . . . . . 154
A. Lösungen aller Übungsaufgaben 155
B. Mathematische Grundlagen
oder: Wieviel Mathematik ist nötig? 167
B.1. Mengen und Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
B.1.1. Der Begriff der Menge . . . . . . . . . . . . . . . . . . . . . . . . . 167
B.1.2. Der Begriff der Funktion . . . . . . . . . . . . . . . . . . . . . . . . 169
B.2. Relationen und Halbordnungen . . . . . . . . . . . . . . . . . . . . . . . . 169
B.3. Formale Logik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
B.3.1. Aussagenlogik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
B.3.2. Prädikatenlogik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
B.3.3. Natürliche und vollständige Induktion . . . . . . . . . . . . . . . . 172

iv Inhaltsverzeichnis

1. Einleitung
1.1. Rechnen und rechnen lassen
Man kann vorzüglich Rechnen lernen, ohne sich jemals zu fragen, was denn das Rechnen
vom sonstigen Gebrauch des Verstandes unterscheidet. Wir stellen diese Frage jetzt und
betrachten dazu das Rechnen so wie es uns im Leben zuerst begegnet — als Umgang mit
den Zahlen. Wir werden also die Natur des Rechnens an der Arithmetik studieren, und
dabei am Ende feststellen, daß die Zahlen bei weitem nicht das Einzige sind, womit wir
rechnen können.
Zweifellos ist Rechnen ein besonderer Gebrauch des Verstandes. Eine gewisse Ahnung
vom Unterschied zwischen Denken im allgemeinen und Rechnen im besonderen hat jeder,
der einmal mit seinem Mathematiklehrer darüber diskutiert hat, ob der Fehler in seiner
Schularbeit „bloß“ als Rechenfehler, oder aber als „logischer“ Fehler einzuordnen sei. Grit Garbo ist Mathematikerin der alten Schule. Für sie gibt es
Richtig Rechnen heißt Anwendung der Rechenregeln für Addition, Multiplikation etc.
Dies allein garantiert das richtige Ergebnis — und neben ihrer Beachtung und Anwendung
ist als einzige weitere Verstandesleistung die Konzentration auf diese eintönige Tätigkeit
gefragt. Kein Wunder, daß nur wenige Menschen zum Zeitvertreib siebenstellige Zahlen
multiplizieren! 1
Damit soll nicht etwa das Rechnen diffamiert werden — es entspricht so gerade der
Natur dessen, worum es dabei geht, nämlich den Zahlen. Diese sind Größen, abstrakte
Quantitäten ohne sonstige Eigenschaft. Bringe ich sie in Verbindung, ergeben sich neue,
andere Größen, aber keine andere Qualität. Der Unterschied von 15 und 42 ist 27, und
daraus folgt — nichts. Die mathematische Differenz zweier Größen ist, so könnte man
sagen, der unwesentliche Unterschied.
Nur zum Vergleich: Stelle ich meinen Beitrag zum Sportverein und meine Einkommenssteuer
einander gegenüber, so ergibt sich auch ein Unterschied im Betrag. Daneben aber
auch einer in der Natur der Empfänger, dem Grad der Freiwilligkeit, meine Einflußmöglichkeiten
auf die Verwendung dieser Gelder und vieles andere mehr. Dies sind wesentliche
Unterschiede, aus ihnen folgt allerhand. Unter anderem erklären sie auch die Differenz
der Beträge, und rechnen sie nicht bloß aus.
Für das Rechnen jedoch spielt es keine Rolle, wovon eine Zahl die Größe angibt. Jede
sonstige Beschaffenheit der betrachteten Objekte ist für das Rechnen mit ihrer Größe oh-
1 Denkaufgabe: Was folgt daraus, wenn einer gut rechnen kann?
eigentlich keine Wissenschaft der Informatik — soweit Informatik
wissenschaftlich ist, gehört sie zur Mathematik, alles andere
ist Ingeniertechnik oder Programmierhandwerk. Fragen der
Programmiersprachen oder des Software Engineering sieht sie
als bloße Äußerlichkeiten an. Sie kann es nicht ganz verschmerzen,
daß die Mathematik von ihrer Tochter Informatik heute in
vielerlei Hinsicht überflügelt wird.

Harry Hacker ist ein alter Programmierfuchs, nach dem Motto:
Eine Woche Programmieren und Testen kann einen ganzen
Nachmittag Nachdenken ersetzen. Er ist einfallsreich und ein
gewitzter Beobachter; allerdings liegt er dabei oft haarscharf
neben der Wahrheit. Zu Programmiersprachen hat er eine dezidiert
subjektive Haltung: Er findet die Sprache am besten, die
ihm am besten vertraut ist.
2 1. Einleitung
ne Belang. Deshalb kann das Rechnen in starre Regeln gegossen werden und nimmt darin
seinen überraschungsfreien Verlauf. Die kreative gedankliche Leistung liegt woanders: Sie
manifestiert sich in der Art und Weise, wie man die abstrakten Objekte der Zahlen konkret
aufschreibt. Wir sind daran gewöhnt, das arabische Stellenwertsystem zu verwenden.
Dieses hat sich im Laufe der Geschichte durchgesetzt, da sich darauf relativ einfach Rechenregeln
definieren und auch anwenden lassen. Das römische Zahlensystem mit seinen
komplizierten Einheiten und der Vor- und Nachstellung blieb auf der Strecke: Den Zahlen
XV und XLII sieht man den Unterschied XXVII nicht an. Insbesondere das Fehlen eines
Symbols für die Null macht systematisches Rechnen unmöglich — gerade wegen der Null
war das Rechnen mit den arabischen Zahlen im Mittelalter von der Kirche verboten.
Einstweiliges Fazit: Das Rechnen ist seiner Natur nach eine äußerliche, gedankenlose, in
diesem Sinne mechanische Denktätigkeit. Kaum hatte die Menschheit Rechnen gelernt,
schon tauchte die naheliegende Idee auf, das Rechnen auf eine Maschine zu übertragen.
Die Geschichte dieser Idee — von einfachen Additionsmaschinen bis hin zu den ersten
programmgesteuerten Rechenautomaten — ist an vielen Stellen beschrieben worden und
soll hier nicht angeführt werden. An ihrem Endpunkt steht der Computer, der bei entsprechender
Programmierung beliebig komplexe arithmetische Aufgaben lösen kann —
schneller als wir, zuverlässiger als wir und (für uns) bequemer.
Wenn dieses Gerät existiert, stellt sich plötzlich eine ganz neue Frage: Jetzt, wo wir
rechnen lassen können, wird es interessant, Aufgaben in Rechenaufgaben zu verwandeln,
die es von Natur aus nicht sind (und die wir mit unserem Verstand auch nie so behandeln
würden). Es gilt, zu einer Problemstellung die richtigen Abstraktionen zu finden, sie durch
Formeln und Rechengesetze, genannt Datenstrukturen und Algorithmen, so weitgehend
zu erfassen, daß wir dem Ergebnis der Rechnung eine Lösung des Problems entnehmen
können. Wir bilden also abstrakte Modelle der konkreten Wirklichkeit, die diese im Falle
der Arithmetik perfekt, in den sonstigen Fällen meist nur annähernd wiedergeben. Die
Wirklichkeitstreue dieser Modelle macht den Reiz und die Schwierigkeit dieser Aufgabe,
und die Verantwortung des Informatikers bei der Software-Entwicklung aus.
Die eigentümliche Leistung der Informatik ist es also, Dinge in Rechenaufgaben zu verwandeln,
die es von Natur aus nicht sind. Die Fragestellung „Was können wir rechnen
lassen?“, ist neu in der Welt der Wissenschaften — deshalb hat sich die Informatik nach
der Konstruktion der ersten Rechner schnell aus dem Schoße der Mathematik heraus zu
einer eigenständigen Disziplin entwickelt. Die Erfolge dieser Bemühung sind faszinierend,
und nicht selten, wenn auch nicht ganz richtig, liest man darüber in der Zeitung: „Computer
werden immer schlauer“.

1.2. Die Aufgabengebiete der Informatik 3
1.2. Die Aufgabengebiete der Informatik
Informatik ist die Wissenschaft vom maschinellen Rechnen. Daraus ergeben sich verschiedene
Fragestellungen, in die sich die Informatik aufgliedert.
Zunächst muß sie sich um die Rechenmaschine selbst kümmern. In der Technischen Informatik
geht es um Rechnerarchitektur und Rechnerentwurf, wozu auch die Entwicklung
von Speichermedien, Übertragungskanälen, Sensoren usw. gehören. Der Fortschritt dieser
Disziplin besteht in immer schnelleren und kleineren Rechnern bei fallenden Preisen. In
ihren elementaren Operationen dagegen sind die Rechner heute noch so primitiv wie zur
Zeit ihrer Erfindung. Diese für den Laien überraschende Tatsache erfährt ihre Erklärung in
der theoretischen Abteilung der Informatik. Lisa Lista ist die ideale Studentin, den Wunschvorstellungen ei-
Mit der Verfügbarkeit der Computer erfolgt eine Erweiterung des Begriffs „Rechnen“.
Das Rechnen mit den guten alten Zahlen ist jetzt nur noch ein hausbackener Sonderfall.
Jetzt werden allgemeinere Rechenverfahren entwickelt, genannt Algorithmen, die
aus Eingabe-Daten die Ausgabe-Daten bestimmen. Aber — was genau läßt sich rechnen,
und was nicht? Mit welcher Maschine? Die Theoretische Informatik hat diese Frage beantwortet
und gezeigt, daß es nicht berechenbare Probleme 2 gibt, d.h. Aufgaben, zu deren
Lösung es keinen Algorithmus gibt. Zugleich hat sie gezeigt, daß alle Rechner prinzipiell
gleichmächtig sind, sofern sie über einige wenige primitive Operationen verfügen. Dagegen
erweisen sich die berechenbaren Aufgaben als unterschiedlich aufwendig, so daß die
Untersuchung des Rechenaufwands, Komplexitätstheorie, heute ein wichtiges Teilgebiet
der Theoretischen Informatik darstellt.
Zwischen den prinzipiellen Möglichkeiten des Rechnens und dem Rechner mit seinen
primitiven Operationen klafft eine riesige Lücke. Die Aufgabe der Praktischen Informatik
ist es, den Rechner für Menschen effektiv nutzbar zu machen. Die „semantische Lücke“
wird Schicht um Schicht geschlossen durch Programmiersprachen auf immer höherer Abstraktionsstufe.
Heute können wir Algorithmen auf der Abstraktionsstufe der Aufgabenstellung
entwickeln und programmieren, ohne die ausführende Maschine überhaupt zu
kennen. Dies ist nicht nur bequem, sondern auch wesentliche Voraussetzung für die Übertragbarkeit
von Programmen zwischen verschiedenen Rechnern. Ähnliches gilt für die Benutzung
der Rechner (Betriebssysteme, Benutzeroberflächen), für die Organisation großer
Datenmengen (Datenbanken) und sogar für die Kommunikation der Rechner untereinander
(Rechnernetze, Verteilte Systeme). Das World Wide Web (WWW) ist das jüngste und
bekannteste Beispiel für das Überbrücken der semantischen Lücke: Es verbindet einfach-
2 Man kann solche Aufgaben auch als Ja/Nein-Fragestellungen formulieren und nennt sie dann „formal unentscheidbare“
Probleme. Läßt man darin das entscheidende Wörtchen „formal“ weg, eröffnen sich tiefsinnige,
aber falsche Betrachtungen über Grenzen der Erkenntnis.
nes überarbeitetenn Hochschullehrers entsprungen. Sie ist unvoreingenommen
und aufgeweckt, greift neue Gedanken auf
und denkt sie in viele Richtungen weiter. Kein Schulunterricht
in Informatik hat sie verdorben. Lisa Lista ist 12 Jahre alt.

Peter Paneau ist Professor der Theoretischen Informatik. Er
sieht die Informatik im wesentlichen als eine formale Disziplin.
Am vorliegenden Text stört ihn die saloppe Redeweise und die
Tatsache, daß viele tiefgründige theoretische Probleme grob vereinfacht
oder einfach umgangen werden. An solchen Stellen erhebt
er mahnend der Zeigefinger . . .
4 1. Einleitung
ste Benutzbarkeit mit globalem Zugriff auf Informationen und andere Ressourcen in aller
Welt. Heute bedarf es nur eines gekrümmten Zeigefingers, um tausend Computer in aller
Welt für uns arbeiten zu lassen.
In der Angewandten Informatik kommt endlich der Zweck der ganzen Veranstaltung
zum Zuge. Sie wendet die schnellen Rechner, die effizienten Algorithmen, die höheren
Programmiersprachen und ihre Übersetzer, die Datenbanken, die Rechnernetze usw. an,
um Aufgaben jeglicher Art sukzessive immer vollkommener zu lösen. Je weiter die Informatik
in die verschiedensten Anwendungsgebiete vordringt, desto spezifischer werden
die dort untersuchten Fragen. Vielleicht werden wir bald erleben, daß sich interdisziplinäre
Anwendungen als eigenständige Disziplinen von der „Kerninformatik“ abspalten.
Wirtschaftsinformatik und Bioinformatik sind mögliche Protagonisten einer solchen Entwicklung.
Während es früher Jahrhunderte gedauert hat, bis aus den Erfolgen der Physik
zunächst die anderen Natur-, dann die Ingenieurwissenschaften entstanden, so laufen
heute solche Entwicklungen in wenigen Jahrzehnten ab.
Wenn die Rechner heute immer mehr Aufgaben übernehmen, für die der Mensch den
Verstand benutzt, so ist insbesondere für Laien daran längst nicht mehr erkennbar, auf
welche Weise dies erreicht wird. Es entsteht der Schein, daß das analoge Resultat auch
in analoger Weise zustande käme. Diesen Schein nennt man künstliche Intelligenz, und
seiner Förderung hat sich das gleichnamige Arbeitsfeld der Informatik gewidmet. Es lohnt
sich, die Metapher von der Intelligenz des Rechners kurz genauer zu betrachten, weil
sie — unter Laien wie unter Informatikern — manche Verwirrung stiftet. Es ist nichts
weiter dabei, wenn man sagt, daß ein Rechner (oder genauer eine bestimmte Software)
sich intelligent verhält, wenn er (oder sie) eine Quadratwurzel zieht, eine WWW-Seite
präsentiert oder einen Airbus auf die Piste setzt. Schließlich wurden viele Jahre Arbeit
investiert, um solche Aufgaben rechnergerecht aufzubereiten, damit der Rechner diese
schneller und zuverlässiger erledigen kann als wir selbst. Nimmt man allerdings die Metapher
allzu wörtlich, kommt man zu der Vorstellung, der Rechner würde dadurch selbst
so etwas wie eine eigene Verständigkeit erwerben. Daraus entsteht gelegentlich sogar die
widersprüchliche Zielsetzung, den Rechner so zu programmieren, daß er sich nicht mehr
wie ein programmierter Rechner verhält. Der Sache nach gehört die „Künstliche Intelligenz“
der Angewandten Informatik an, geht es ihr doch um die erweiterte Anwendbarkeit
des Rechners auf immer komplexere Probleme. Andererseits haben diese konkreten
Anwendungen für sie nur exemplarischen Charakter, als Schritte zu dem abstrakten Ziel,
„wirklich“ intelligente künstliche Systeme zu schaffen. So leidet diese Arbeitsrichtung unter
dem Dilemma, daß ihr Beitrag zum allgemeinen Fortschritt der Informatik vom Lärm
der immer wieder metaphorisch geweckten und dann enttäuschten Erwartungen übertönt
wird.
Unbeschadet solch metaphorischer Fragen geht der Vormarsch der Informatik in allen
Lebensbereichen voran — der „rechenbare“ Ausschnitt der Wirklichkeit wird ständig er-

1.3. Einordnung der Informatik in die Familie der Wissenschaften 5
weitert: Aus Textverarbeitung wird DeskTop Publishing, aus Computerspielen wird Virtual
Reality, und aus gewöhnlichen Bomben werden „intelligent warheads“. Wie gesagt: die
Rechner werden immer schlauer. Und wir?
1.3. Einordnung der Informatik in die Familie der
Wissenschaften
Wir haben gesehen, daß die Grundlagen der Informatik aus der Mathematik stammen,
während der materielle Ausgangspunkt ihrer Entwicklung die Konstruktion der ersten Rechenmaschinen
war. Mutter die Mathematik, Vater der Computer — wissenschaftsmoralisch
gesehen ist die Informatik ein Bastard, aus einer Liebschaft des reinen Geistes mit
einem technischen Gerät entstanden.
Die Naturwissenschaft untersucht Phänomene, die ihr ohne eigenes Zutun gegeben
sind. Die Gesetze der Natur müssen entdeckt und erklärt werden. Die Ingenieurwissenschaften
wenden dieses Wissen an und konstruieren damit neue Gegenstände, die selbst
wieder auf ihre Eigenschaften untersucht werden müssen. Daraus ergeben sich neue Verbesserungen,
neue Eigenschaften, und so weiter.
Im Vergleich dieser beiden Abteilungen der Wissenschaft steht die Informatik eher den
Ingenieurwissenschaften nahe: Auch sie konstruiert Systeme, die — abgesehen von denen
der Technischen Informatik — allerdings immateriell sind. Wie die Ingenieurwissenschaften
untersucht sie die Eigenschaften ihrer eigenen Konstruktionen, um sie weiter zu
verbessern. Wie bei den Ingenieurwissenschaften spielen bei der Informatik die Aspekte
der Zuverlässigkeit und Lebensdauer ihrer Produkte eine wesentliche Rolle.
Eine interessante Parallele besteht auch zwischen Informatik und Rechtswissenschaft.
Die Informatik konstruiert abstrakte Modelle der Wirklichkeit, die dieser möglichst nahe
kommen sollen. Das Recht schafft eine Vielzahl von Abstraktionen konkreter Individuen.
Rechtlich gesehen sind wir Mieter, Studenten, Erziehungsberechtigte, Verkehrsteilnehmer,
etc. Als solche verhalten wir uns entsprechend der gesetzlichen Regeln. Der Programmierer
bildet reale Vorgänge in formalen Modellen nach, der Jurist muß konkrete Vorgänge
unter die relevanten Kategorien des Rechts subsumieren. Die Analogie endet allerdings,
wenn eine Diskrepanz zwischen Modell und Wirklichkeit auftritt: Bei einem Programmfehler
behält die Wirklichkeit recht, bei einem Rechtsbruch das Recht.
Eine wissenschaftshistorische Betrachtung der Informatik und ihre Gegenüberstellung
mit der hier gegebenen deduktiven Darstellung ist interessant und sollte zu einem späteren
Zeitpunkt, etwa zum Abschluß des Informatik-Grundstudiums, nachgeholt werden.
Interessante Kapitel dieser Geschichte sind das Hilbert’sche Programm, die Entwicklung
der Idee von Programmen als Daten, die oben diskutierte Idee der „Künstlichen Intelligenz“,
der Prozeß der Loslösung der Informatik von der Mathematik, die Geschichte der

6 1. Einleitung
Programmiersprachen, die Revolution der Anwendungssphäre durch das Erscheinen der
Mikroprozessoren, und vieles andere mehr.

2. Modellierung
Wir haben im ersten Kapitel gelernt: Programmieren heißt, abstrakte Modelle realer Objekte
zu bilden, so daß die Rechenregeln im Modell die relevanten Eigenschaften in der
Wirklichkeit adäquat nachbilden.
Wir werden den Vorgang der Modellierung nun anhand von zwei Beispielen kennen
lernen.
2.1. Eine Formelsprache für Musik
Wir haben gelernt, daß die Welt der Zahlen wegen ihres formalen Charakters die natürliche
Heimat des Rechnens ist. Es gibt ein zweites Gebiet, in dem ein gewisser Formalismus
in der Natur der Sache liegt: die Musik.
Das Spielen eines Musikstückes mag vieles sein – ein künstlerischer Akt, ein kulturelles
oder emotionales Ereignis. Im Kern jedoch steht das Musikstück – es bringt die Musikvorstellung
des Komponisten in eine objektive Form und ist nichts anderes als ein Programm
zur Ausführung durch einen Musiker (oder heute über eine Midi-Schnittstelle auch durch
einen elektronischen Synthesizer). Wer immer als erster ein Musikstück niedergeschrieben
hat, hat damit den Schritt vom Spielen zum Spielen lassen begründet.
Diese kulturhistorische Leistung ist viel älter als die Idee einer Rechenmaschine. In der
traditionellen Notenschrift ist der formale Anteil der Musik manifestiert. Die Modellierung
ist hier also bereits erfolgt, allerdings ausschließlich im Hinblick auf die Wiedergabe durch
einen menschlichen Interpreten, und nicht bis hin zur Entwicklung von dem Rechnen
vergleichbaren Regeln. Zwar sind viele Gesetze z.B. der Harmonielehre bekannt, man kann
sie aber in der Notenschrift nicht ausdrücken. So kann man zwar jeden Dur-Dreiklang
konkret hinschreiben – aber die allgemeine Aussage, daß ein Dur-Dreiklang immer aus
einem großen und einem kleinen Terz besteht, muß auf andere Art erfolgen. In diesem
Abschnitt setzen wir die Notenschrift (natürlich nur einen kleinen Ausschnitt davon) in
eine Formelsprache samt den zugehörigen Rechenregeln um.
Musikstücke sind aus Noten zusammengesetzt, die gleichzeitig oder nacheinander gespielt
werden. Jede Note hat einen Ton und eine Dauer. Dem Stück als Ganzem liegt ein
bestimmter Takt zugrunde, und die Dauer einzelner Töne wird in Takt-Bruchteilen gemessen.
Die Tonskala besteht aus 12 Halbtönen, die sich in jeder Oktave wiederholen.

8 2. Modellierung
Wir legen das tiefe C als untersten Ton zugrunde und numerieren die Halbtöne von 0
ab aufwärts. Angaben zum Spieltempo (in Taktschlägen pro Minute) und zur Wahl des
Instruments werden global für ganze Musikstücke gemacht.
Formeln, die Musik bedeuten, können wir uns z.B. so vorstellen:
Note 0 (1/4) -- Viertelnote tiefes C
Note 24 (1/1) -- ganze Note c’
Pause (1/16) -- Sechzehntelpause
Note 24 (1/4) :*: Note 26 (1/4) :*: Note 28 (1/4)
-- Anfang der C-Dur Tonleiter
Note 24 (1/4) :+: Note 28 (1/4) :+: Note 31 (1/4)
-- C-Dur Akkord
Tempo 40 m -- Musik m als Adagio
Tempo 100 m -- Musik m als Presto
Instr Oboe m -- Musik m von Oboe gespielt
Instr VoiceAahs m -- Musik m gesummt
Wir konstruieren nun die Formelwelt, deren Bürger die obigen Beispiele sind. Wir gehen
davon aus, daß es Formeln für ganze Zahlen, Brüche und ein bißchen Arithmetik bereits
gibt in der Formelwelt und führen neue Typen von Formeln ein: Ton, Dauer, Instrument
und Musik.
infixr 7 :*:
infixr 6 :+:
type GanzeZahl = Int -- Ganze Zahlen und Brueche setzen wir
type Bruch = Rational -- als gegeben voraus.
type Ton = GanzeZahl
type Dauer = Bruch
data Instrument = Oboe | HonkyTonkPiano |
Cello | VoiceAahs deriving Show
data Musik = Note Ton Dauer |
Pause Dauer |
Musik :*: Musik |
Musik :+: Musik |
Instr Instrument Musik |
Tempo GanzeZahl Musik deriving Show
Die neuen Formeltypen Ton und Dauer sind nur Synonyme für ganze Zahlen und Brüche
entsprechend der besonderen Bedeutung, in der wir sie gebrauchen. Sie tragen keine
neuen Formeln bei. Anders bei Instrument und Musik. Die Symbole Note, Pause,
:*:, :+:, Instr, Tempo sind die Konstruktoren für neuartige Formeln, die Musikstücke
darstellen. In der Formel m1 :*: m2 dürfen (und müssen!) m1 und m2 beliebige
Formeln für Musikstücke sein, insbesondere selbst wieder zusammengesetzt.

2.1. Eine Formelsprache für Musik 9
In Anlehnung an die Punkt-vor-Strich Regel der Algebra geben wir der Verknüpfung
von Noten zu einer zeitlichen Abfolge (:*:) Vorrang vor der zeitlich parallelen Verknüpfung
mehrerer Stimmen (:+:). Damit ist die Formel m1 :+: m2 :*: m3 zu lesen als
m1 :+: (m2 :*: m3).
Umfangreiche Musikstücke können nun als wahre Formelgebirge geschrieben werden.
Zuvor erleichtern wir uns das Leben in der Formelwelt, indem wir einige Abkürzungen
einführen. Etwa für die Pausen:
gP = Pause (1/1)
hP = Pause (1/2)
vP = Pause (1/4)
aP = Pause (1/8)
sP = Pause (1/16)
Diese Definitionen sind zugleich Rechenregeln. Sie bedeuten einerseits, daß man die
neuen Symbole gP, hP, vP, aP, sP überall in Musikstücken einsetzen kann – es erweitert
sich damit die Formelwelt. Zugleich kann man jedes Symbol jederzeit durch die
rechte Seite der Definition ersetzen – so daß die Musikstücke in der Formelwelt nicht
mehr geworden sind.
Hier sind klangvolle Namen für einige Tempi:
adagio = 70; andante = 90; allegro = 140; presto = 180
Die üblichen Bezeichnungen für die 12 Halbtöne führen wir so ein:
ce = 0; cis = 1; des = 1
de = 2; dis = 3; es = 3
eh = 4; eis = 5; fes = 4
ef = 5; fis = 6; ges = 6
ge = 7; gis = 8; as = 8
ah = 9; ais = 10; be = 10
ha = 11; his = 12
Diese Töne sind in der untersten Oktave angesiedelt, und wir brauchen sie hier kaum.
Dagegen brauchen wir eine bequeme Notation für Noten (beliebiger Dauer) aus der C-
Dur Tonleiter in der dritten Oktave:
c’ u = Note (ce+24) u; d’ u = Note (de+24) u
e’ u = Note (eh+24) u; f’ u = Note (ef+24) u
g’ u = Note (ge+24) u; a’ u = Note (ah+24) u
h’ u = Note (ha+24) u; c’’ u = Note (ce+36) u
Als Beispiele hier der C-Dur Akkord in neuer Schreibweise, sowie eine (rhythmisch beschwingte)
C-Dur Tonleiter:

10 2. Modellierung
cDurTonika = c’ (1/1) :+: e’ (1/1) :+: g’ (1/1)
cDurSkala = Tempo allegro(
c’ (3/8) :*: d’ (1/8) :*: e’ (3/8) :*: f’ (4/8)
:*: g’ (1/8) :*: a’ (1/4) :*: h’ (1/8) :*: c’’ (1/2))
Allgemein gesagt, besteht ein Dur-Dreiklang aus einen Grundton t sowie der großen
Terz und der Quinte über t.
Dieses Gesetz als Formel:
durDreiklang t = Note t (1/1) :+: Note (t+4) (1/1) :+: Note (t+7) (1/1)
Wie wär’s mit einer allgemeinen Regel zur Umkehrung eines Dreiklangs (der unterste
Ton muß eine Oktave nach oben)?
umk ((Note t d) :+: n2 :+: n3) = n2 :+: n3 :+: (Note (t+12) d)
Als komplexe Operation auf ganzen Musikstücken betrachten wir das Transponieren.
Es bedeutet, daß Töne um ein gewisses Intervall verschoben werden, während alles andere
gleich bleibt. Wie muß die Rechenregel lauten, um Musikstück m um Intervall i zu
transponieren? Wir geben eine Regel für jede mögliche Form von m an:
transponiere i (Pause d) = Pause d
transponiere i (Note t d) = Note (t+i) d
transponiere i (m1 :*: m2) = (transponiere i m1) :*: (transponiere i m2)
transponiere i (m1 :+: m2) = (transponiere i m1) :+: (transponiere i m2)
transponiere i (Instr y m) = Instr y (transponiere i m)
transponiere i (Tempo n m) = Tempo n (transponiere n m)
gDurTonika = transponiere 7 cDurTonika
Da das Transponieren Intervalle nicht ändert, führt es einen Dur-Dreiklang wieder in
einen Dur-Dreiklang über. Es gilt folgendes Gesetz für beliebigen Grundton g und beliebiges
Intervall i:
transponiere i (durDreiklang t) = durDreiklang(t+i)
Zur Überprüfung rechnen wir beide Seiten mittels der Definition von transponiere
und durDreiklang aus und erhalten beide Male
Note (t+i) (1/1) :+: Note (t+4+i) (1/1) :+: Note (t+7+i) (1/1)

2.2. Typen als Hilfsmittel der Modellierung 11
Hier haben wir eine Methode zur Validierung von Modellen kennengelernt: Wenn man
beweisen kann, daß ein Gesetz der realen Welt auch in der Formelwelt gilt, so gibt das
Modell die Wirklichkeit zumindest in dieser Hinsicht treu wieder.
Bevor wir ein komplettes Lied zusammenstellen, hier zwei Regeln zur Wiederholung:
wdh m = m :*: m
ad_infinitum m = m :*: ad_infinitum m
Einen um Dauer d verzögerten Einsatz erhält man durch Vorschalten einer Pause.
einsatz d m = (Pause d) :*: m
Unser letztes Beispiel beschreibt den Kanon „Bruder Jakob“, wobei wir die 2. Stimme
eine Oktave über den anderen notieren.
phrase1 = c’ (1/4) :*: d’ (1/4) :*: e’ (1/4) :*: c’ (1/4)
phrase2 = e’ (1/4) :*: f’ (1/4) :*: g’ (1/2)
phrase3 = g’ (1/8) :*: a’ (1/8) :*: g’ (1/8) :*: f’ (1/8)
:*: e’ (1/4) :*: c’ (1/4)
phrase4 = c’ (1/4) :*: (transponiere (-12) (g’ (1/4))) :*: c’’ (1/2)
strophe = wdh phrase1 :*: wdh phrase2 :*: wdh phrase3 :*: wdh phrase4
endlos = ad_infinitum strophe
bruderJakob = Tempo andante (Instr VoiceAahs
(einsatz (0/1) endlos :+:
(einsatz (2/1) (transponiere 12 endlos)) :+:
(einsatz (4/1) endlos) :+:
(einsatz (6/1) endlos )))
Natürlich gehört zu einer praktischen Formelsprache für Musik noch vieles, was wir hier
nicht betrachtet haben – Text, Artikulation, Kontrapunkt, eine Möglichkeit zur Übersetzung
der Formeln in die traditionelle Notation und in eine Folge von Midi-Befehlen, um
damit einen Synthesizer zu steuern.
2.2. Typen als Hilfsmittel der Modellierung
In der realen Welt verhindert (meistens) die Physik, daß unpassende Operationen mit
untauglichen Objekten ausgeführt werden. Man kann eben einen Golfball nicht unter einer
Fliege verstecken oder einen Rosenbusch mit einer Steuererklärung paaren. Macht

12 2. Modellierung
es Sinn, einer streikenden (?) Waschmaschine gut zuzureden? Das Problem in einer Formelwelt
ist, daß man zunächst alles hinschreiben kann, weil die Formeln sich nicht selbst
dagegen sträuben.
Aus diesem Grund gibt man jedem Objekt des Modells einen Typ, der eine Abstraktion
der natürlichen Eigenschaften des realen Objekts ist.
In der Formelsprache für Musik haben wir die Typen Ton (synonym für ganzeZahl) und
Dauer (synonym für positive rationale Zahl) vorausgesetzt und die Typen Musik und
Instrument neu eingeführt. Die Typendeklaration legt nicht nur fest, daß Musik auf
sechs verschiedene Weisen zusammengesetzt werden kann, und zwar durch die (Formel-)
Konstruktoren Note bis Tempo. Sie sagt auch, welche Formeln zusammengefügt werden
dürfen. Note muß stets einen Ton mit einer Dauer verknüpfen. Mit :*: kann man zwei
Musikstücke verknüpfen, nicht aber ein Musikstück mit einem Ton. Folgende Formeln
sind fehlerhaft:
Note 3/4 ce Pause (1/2 :*: 1/4)
Pause Cello Instr (Cello :+: Oboe) cDurTonika
Tempo Oboe 100 c’ :+: e’ :+: g’
Möglicherweise hat sich der Autor dieser Formeln etwas Sinnvolles gedacht – aber es
muß in unserer Formelsprache anders ausgedrückt werden. Auch die durch Definitionen
eingeführten Namen erhalten einen Typ. Er ergibt sich aus der rechten Seite der definierenden
Gleichung. Wir schreiben a, b, c :: t für die Aussage „Die Namen (oder Formeln)
a, b, c haben Typ t“ und stellen fest:
ce, cis, des, de, dis, es, eh, eis, fes, ef, fis :: Ton
ges, ge, gis, as, ah, ais, be, ha, his :: Ton
gP, hP, vP, aP, sP :: Musik
cDurTonika :: Musik
adagio, andante, allegro, presto :: GanzeZahl
Die Namen c’, d’ etc. bezeichnen Funktionen, die eine Dauer als Argument und
Musik als Ergebnis haben. umk, wdh und ad_infinitum wandeln Musikstücke um.
c’, d’, e’, f’, g’, a’, h’, c’’ :: Dauer -> Musik
umk, wdh, ad_infinitum :: Musik -> Musik
transponiere schließlich hat zwei Argumente, was wir – etwas gewöhnugsbedürftig
– mit zwei Funktionspfeilen ausdrücken.
transponiere :: GanzeZahl -> Musik -> Musik

2.3. Die Rolle der Abstraktion in der Modellierung 13
Hinter dieser Notation steht die Sichtweise, daß man einer zweistelligen Funktion wie
transponiere manchmal nur ein Argument geben möchte: Unter
(transponiere 7) stellen wir uns eine abgeleitete Funktion vor, die Musikstücke um
eine Quinte nach oben transponiert. Natürlich hat (transponiere 7) dann den „restlichen“
Typ Musik -> Musik.
2.3. Die Rolle der Abstraktion in der Modellierung
Unsere Formelsprache für Musik erlaubt es, in direkter Analogie zur Notenschrift Musikstücke
als Formeln hinzuschreiben. Darüberhinaus können wir aber auch abstrakte Zusammenhänge
zwischen Musikstücken darstellen, wie etwa den Aufbau eines Dur-Dreiklangs
oder das Transponieren. Worauf beruht dies Möglichkeit?
Sie beginnt damit, daß wir beliebige Formeln mit einem Namen versehen können, wie
etwa bei gP, hP oder phrase1 bis phrase4. Diese Namen sind kürzer und (hoffentlich)
lesbarer als die Formeln, für die sie stehen, aber noch nicht abstrakter. Die Abstraktion
kommt mit dem Übergang zu Funktionen ins Spiel. Vergleichen wir die beiden folgenden
Definitionen eines Zweiklangs:
tritonus_f_1 = Note ef (1/1) :+: Note ha (1/1)
tritonus t d = Note t d :+: Note (t+6) d
tritonus_f_1 beschreibt einen Zweiklang von konkreter Tonlage und Dauer.
tritonus dagegen abstrahiert von Tonlage und Dauer, und hält nur fest, was für den als
Tritonus bekannten Zweiklang wesentlich ist — ein Intervall von 6 Halbtonschritten.
Dieser Unterschied macht sich auch an den Typen bemerkbar. Wir finden:
tritonus_f_1 :: Musik
tritonus :: Ton -> Dauer -> Musik
Hier verrät uns bereits der Typ, daß in der Formel tritonus erst Ton und Dauer konkretisiert
werden müssen, ehe spielbare Musik entsteht. Bei den Noten der eingestrichenen
C-Dur-Skala (c’, d’, ...) haben wir von der Dauer abtrahiert, sonst hätten wir Definitionen
für 40 oder noch mehr Namen einführen müssen. Andererseits haben wir hier
natürlich nicht vom Ton abstrahiert, wir wollten ja Namen für bestimmte Töne einführen.
Und außerdem gibt es diese Abstraktion bereits: Eine Note von beliebigem Ton und
Dauer wird gerade von dem Konstruktor Note repräsentiert, dem wir daher auch den Typ
Ton -> Dauer -> Musik zuordnen.
Typen halten die Objekte der Formelwelt auseinander, Funktionen stiften Zusammenhänge.
Wollten wir ohne Abstraktion das Prinzip der Umkehrung eines Dreiklangs beschreiben,
kämen wir über konkrete Beispiele nicht hinaus. Die Funktion umk leistet das

14 2. Modellierung
Gewünschte mühelos. Und schließlich hält uns nichts davon ab (Übungsaufgabe!), im Kanon
bruderJakob von der eigentlichen Melodie zu abstrahieren und ein allgemeines
Konstruktionsprinzip für einen vierstimmigen Kanon anzugeben.
Hier haben wir die Methode der funktionalen Abstraktion kennengelernt. Technisch
gesehen besteht sie lediglich darin, in einer Formel einige Positionen als variabel zu betrachten.
So wird aus der Formel eine Funktion, die mit einem Namen versehen und in
vielfältiger Weise eingesetzt werden kann, und die zugleich selbst ein abstraktes Prinzip
repräsentiert. Wir werden später noch andere Formen der Abstraktion kennenlernen, aber
die funktionale Abstraktion ist sicher die grundlegendste von allen.
2.4. Modellierung in der molekularen Genetik
Die Basen Adenin, Cytosin, Guanin und Thymin bilden zusammen mit Phosphor und Ribose
die Nukleotide, die Bausteine der Erbsubstanz.
data Nucleotide = A | C | G | T deriving (Eq, Show)
Die 20 Aminosäuren sind die Bausteine aller Proteine:
data AminoAcid = Ala -- Alanin
| Arg -- Arginin
| Asn -- Asparagin
| Asp -- Aspartat
| Cys -- Cystein
| Gln -- Glutamin
| Glu -- Glutamat
| Gly -- Glycin
| His -- Histidin
| Ile -- Isoleucin
| Leu -- Leucin
| Lys -- Lysin
| Met -- Methionin
| Phe -- Phenylalanin
| Pro -- Prolin
| Ser -- Serin
| Thr -- Threonin
| Trp -- Tryptophan
| Tyr -- Tyrosin
| Val -- Valin
| Stp -- keine Aminosaeure; siehe unten
deriving (Eq, Show)

2.4. Modellierung in der molekularen Genetik 15
Lange Ketten von Nukleotiden bilden die Nukleinsäure, lange Ketten von Aminosäuren
bilden Proteine. Chemisch werden diese Ketten auf unterschiedliche Weise gebildet:
Bei den Nukleotiden verknüpfen die Phosphor-Atome die Ribose-Ringe, zwischen den
Aminosäuren werden Peptidbindungen aufgebaut. Da wir aber die Chemie der Moleküle
nicht modellieren wollen, wollen wir auch nicht unterscheiden, auf welche Weise die
Ketten konstruiert werden. Als Formel für Kettenmoleküle schreiben wir
A:C:C:A:G:A:T:T:A:T:A:T: ..., oder
Met:Ala:Ala:His:Lys:Lys:Leu: ...
Im Unterschied zur Molekularbiologie kennt also unsere Formelwelt einen Konstruktor
(:), der Ketten jeglicher Art aufbaut:
data [a] = [] -- leere Kette
| a:[a] -- (:) verlaengert Kette von a’s um ein a.
Den Datentyp [a] nennt man einen polymorphen Listentyp. Hier ist a ein Typparameter.
Dies bedeutet, das Elemente beliebigen, aber gleichen Typs mittels der Konstruktoren
(:) und [] zu Listen zusammengefügt werden können. Für Listen führen wir eine spezielle
Notation ein: Statt a:b:c:[] schreiben wir auch [a,b,c].
Damit können wir nun sagen, welcher Datentyp in der Formelwelt den realen Nukleinsäuren
und Proteinen entsprechen soll:
type DNA = [Nucleotide]
type Protein = [AminoAcid]
type Codon = (Nucleotide, Nucleotide, Nucleotide)
Im Ruhezustand (als Informationsspeicher) ist die DNA allerdings ein Doppelmolekül:
Zwei DNA-Stränge bilden die berühmte, von Watson und Crick entdeckte Doppelhelix.
Sie beruht darauf, daß bestimmte Basen zueinander komplementär sind - sie können Wasserstoffbrückenbindungen
aufbauen, wenn sie einander gegenüber stehen.
wc_complement A = T
wc_complement T = A
wc_complement C = G
wc_complement G = C
Wir können die dopplesträngige DNA auf zwei verschiedene Weisen darstellen, als Paar
von Listen oder als Liste von Paaren.
type DNA_DoubleStrand = (DNA,DNA) -- als Paar zweier Einzelstraenge
type DNA_DoubleStrand’ = [(Nucleotide,Nucleotide)]
-- als Kette von Watson-Crick-Paaren
dnaDS_Exmpl1 = ([A,C,C,G,A,T],[T,G,G,C,T,A])
dnaDS_Exmpl2 = [(A,T),(C,G),(C,G),(G,C),(A,T),(T,A)]

16 2. Modellierung
Dabei ist die erste Version deutlich vorzuziehen. Sie deutet an, was in der Zelle auch
stattfindet: Das Aufspalten oder Zusammenfügen des Doppelstrangs aus zwei Einzelsträngen.
Die zweite Version dagegen suggeriert, daß existierende Watson-Crick Basenpaare zu
einer Doppelkette verknüpft werden. Einzelne solche Paare sind jedoch wegen der sehr
schwachen Wasserstoffbindung nicht stabil und kommen daher in der Zelle nicht vor.
Wir entscheiden uns also für den Datentyp DNA_DoubleStrand. So naheliegend seine
Definition auch erscheint, sie ist nicht ohne Gefahren: Formeln vom Typ
DNA_DoubleStrand sollen beliebige doppelsträngige DNA-Moleküle darstellen. Das können
sie auch. Aber darüber hinaus können wir formal korrekte Formeln des Typs
DNA_DoubleStrand hinschreiben, denen keine Doppelhelix entspricht.
incorrectDoubleStrand = ([A,C,C,G,A,T],[T,G,G,C,A,T,C])
incorrectDoubleStrand ist in zweifacher Weise falsch: Erstens sind die jeweiligen
Basen an mehreren Stellen nicht komplementär, und zweitens haben die beiden Einzelstränge
gar noch unterschiedliche Länge. Wir stoßen hier auf eine grundlegende Schwierigkeit
bei jeder Modellierung: Es gibt Objekte in der Modellwelt, die nichts bedeuten,
d.h. denen keine Objekte der Wirklichkeit entsprechen. Solche Formeln, die wohlgebaut,
aber ohne Bedeutung sind, nennt man syntaktisch korrekt, aber semantisch falsch. Alles
geht gut, solange beim Rechnen mit den Formeln auch keine solchen Objekte erzeugt
werden. Wenn doch, sind die Folgen meist unabsehbar. Im besten Fall bleibt die Rechnung
irgendwann stecken, weil eine Funktion berechnet werden soll, die für solche Fälle
keine Regel vorsieht. Manchmal passen die Rechenregeln auch auf die nicht vorgesehenen
Formeln, und dann kann es im schlimmsten Fall geschehen, daß die Rechnung ein
Ergebnis liefert, dem man nicht ansieht, daß es falsch ist.
Wir werden sehen, daß selbst die Natur im Falle der DNA-Replikation dieses Problem
erkannt und einen Weg zu seiner Lösung gefundenhat. Zunächst betrachten wir
den „Normalfall“ der Replikation. Weil das Komplement jeder Base eindeutig definiert
ist, kann man zu jedem DNA-Einzelstrang den komplementären Doppelstrang berechnen.
In der Tat geschieht dies bei der Zellteilung. Der Doppelstrang wird aufgespalten, und
die DNA-Polymerase synthetisiert zu jedem der beiden Stränge den jeweils komplementären
Strang. Die DNA-Polymerase können wir auf zwei verschiedene Weisen darstellen:
Enerseits ist sie ein Enzym, also selbst ein Protein:
dnaPolymerase_Sequenz = Met:Ala:Pro:Val:His:Gly:Asp:Asp:Ser ...
Dies hilft uns allerdings nicht dabei, die Wirkungsweise dieses Enzyms auszudrücken.
Noch viele Jahrzehnte werden vergehen, ehe die Wissenschaft die Funktion eines Proteins
aus der Kette seiner Aminosäuren ableiten kann. Was liegt also näher, als die Funktion der
Polymerase durch eine Funktion zu modellieren:

2.4. Modellierung in der molekularen Genetik 17
dnaPolymerase :: DNA -> DNA_DoubleStrand
dnaPolymerase x = (x, complSingleStrand x) where
complSingleStrand [] = []
complSingleStrand (a:x) = wc_complement a:complSingleStrand x
Will man prüfen (lassen), ob ein Dopplestrang tatsächlich korrekt aufgebaut ist, kann
man dies nun einfach tun.
data Bool = True | False -- die abstrakten Urteile Wahr und Falsch
wellFormedDoubleStrand :: DNA_DoubleStrand -> Bool
wellFormedDoubleStrand (x,y) = (x,y) == dnaPolymerase x
(Zur Unterscheidung von der definierenden Gleichung schreiben wir den Vergleich zweier
Formeln als ==. Dabei werden beide Formeln zunächst ausgerechnet und dann verglichen.)
Blickt man etwas tiefer ins Lehrbuch der Genetik, so findet man, daß auch die Natur
nicht ohne Fehler rechnet: Mit einer (sehr geringen) Fehlerrate wird in den neu polymerisierten
Strang ein falsches (nicht komplementäres) Nukleotid eingebaut. Dadurch wird die
Erbinformation verfälscht. Daher gibt es ein weiteres Enzym, eine Exonuclease, die fehlerhafte
Stellen erkennt und korrigiert. Sie muß dabei ein subtiles Problem lösen: Gegeben
ein Doppelstrang mit einem nicht komplementären Basenpaar darin – welcher Strang ist
das Original, und welcher muß korrigiert werden? Die Natur behilft sich dadurch, daß der
Originalstrang beim Kopieren geringfügig modifiziert wird – durch Anhängen von Methylgruppen
an seine Nukleotide.
Diese Technik können wir nicht einsetzen, da wir die Chemie der Nukleotide nicht modellieren.
Wir behelfen uns auf eine nicht weniger subtile Art: Im Unterschied zur Wirklichkeit
(Doppelhelix) kann man im Modell (DNA_DoubleStrand) einen „linken“ und
„rechten“ Strang unterscheiden. Übereinstimmend mit der Modellierung der Polymerase
legen wir fest, daß stets der „linke“ Strang als Original gilt, der „rechte“ als die Kopie.
Auch die Exonuclease modellieren wir durch ihre Funktion:
exonuclease :: DNA_DoubleStrand -> DNA_DoubleStrand
exonuclease ([],[]) = ([],[])
exonuclease ([],x) = ([],[]) -- Kopie wird abgeschnitten
exonuclease (x,[]) = dnaPolymerase x -- Kopie wird verlaengert
exonuclease (a:x,b:y) = if b == ac then (a:x’,b:y’)
else (a:x’,ac:y’)
where ac = wc_complement a
(x’,y’) = exonuclease (x,y)
Damit erhalten wir z.B. die erwünschte Korrektur des fehlerhaften Doppelstrangs:

18 2. Modellierung
exonuclease incorrectDoubleStrand ==> ([A,C,C,G,A,T],[T,G,G,C,T,A])
Unsere Definition der Exonuclease ist der Natur abgelauscht. Vom Standpunkt des Rechenergebnisses
aus betrachtet (man nennt diesen Standpunkt extensional) können wir
das Gleiche auch einfacher haben: Verläßt man sich darauf, daß unsere DNA-Polymerase
im Modell keine Fehler macht, kann man einfach den kopierten Strang gleich neu polymerisieren.
dnaCorr :: DNA_DoubleStrand -> DNA_DoubleStrand
dnaCorr (x,y) = dnaPolymerase x
Es ist nicht ganz überflüssig, die gleiche Funktion auf verschiedene Weisen zu beschreiben.
Daraus ergibt sich die Möglichkeit, das Modell an sich selbst zu validieren. Es muß
ja nun die folgende Aussage gelten:
Für alle d::DNA_DoubleStrand gilt dnaCorr d == exonuclease d.
Außerdem muß die dnaPolymerase eine Idempotenzeigenschaft aufweisen:
Für alle x::DNA gilt: x == z where (x,y) == dnaPolymerase x
(y,z) == dnaPolymerase y
Wir formulieren solche Eigenschaften, die wir aus der Wirklichkeit kennen, in der Sprache
der Modellwelt. Können wir sie dort als gültig nachweisen, so wissen wir erstens,
daß unser Modell im Hinblick auf genau diese Eigenschaften der Realität entspricht. Aber
noch mehr: Sofern wir diese Eigenschaften beim Formulieren des Modells nicht explizit
bedacht haben, fördert ihr Nachweis auch unser generelles Vertrauen in die Tauglichkeit
des Modells. Wir werden später Techniken kennenlernen, wie man solche Eigenschaften
nachweist.
Fast ohne Ausnahme benutzen alle Lebewesen den gleichen genetischen Code. Bestimmte
Dreiergruppen (genannt Codons) von Nukleotiden codieren für bestimmte Aminosäuren.
Da es 4 3 = 64 Codons, aber nur 20 Aminosäuren gibt, werden viele Aminosäuren
durch mehrere Codons codiert. Einige Codons codieren für keine Aminosäure; man
bezeichnet sie als Stop-Codons, da ihr Auftreten das Ende eines Gens markiert.
Der genetische Code ist also eine Funktion, die Codons auf Aminosäuren abbildet. (Wir
abstrahieren hier davon, daß die DNA zunächst in RNA transkribiert wird, wobei die Base
Thymin überall durch Uracil ersetzt wird.)
genCode :: Codon -> AminoAcid
genCode (A,A,A) = Lys; genCode (A,A,G) = Lys
genCode (A,A,C) = Asn; genCode (A,A,T) = Asn
genCode (A,C,_) = Thr

2.4. Modellierung in der molekularen Genetik 19
genCode (A,G,A) = Arg; genCode (A,G,G) = Arg
genCode (A,G,C) = Ser; genCode (A,G,T) = Ser
genCode (A,T,A) = Ile; genCode (A,T,C) = Ile
genCode (A,T,T) = Ile
genCode (A,T,G) = Met
genCode (C,A,A) = Glu; genCode (C,A,G) = Glu
genCode (C,A,C) = His; genCode (C,A,T) = His
genCode (C,G,_) = Arg
genCode (C,C,_) = Pro
genCode (C,T,_) = Leu
genCode (G,A,A) = Glu; genCode (G,A,G) = Glu
genCode (G,A,C) = Asp; genCode (G,A,T) = Asp
genCode (G,C,_) = Ala
genCode (G,G,_) = Gly
genCode (G,T,_) = Val
genCode (T,A,A) = Stp; genCode (T,A,G) = Stp
genCode (T,G,A) = Stp
genCode (T,A,C) = Tyr; genCode (T,A,T) = Tyr
genCode (T,C,_) = Ser
genCode (T,G,G) = Trp
genCode (T,G,C) = Cys; genCode (T,G,T) = Cys
genCode (T,T,A) = Leu; genCode (T,T,G) = Leu
genCode (T,T,C) = Phe; genCode (T,T,T) = Phe
Ein Gen beginnt stets mit dem „Startcodon“ (A,T,G) , setzt sich dann mit weiteren
Codons fort und endet mit dem ersten Auftreten eines Stopcodons. Die Translation, d.h.
die Übersetzung des Gens in das codierte Protein erfolgt am Ribosom. Dies ist ein sehr
komplexes Molekül, ein Verbund aus Proteinen und Nukleinsäuren. Wir modellieren es
durch seine Funktion:
ribosome :: DNA -> Protein
ribosome (A:T:G:x) = Met:translate (triplets x) where
triplets :: [a] -> [(a,a,a)]
triplets [] = []
triplets (a:b:c:x) = (a,b,c):triplets x
translate :: [Codon] -> Protein
translate [] = []
translate (t:ts) = if aa == Stp then []
else aa:translate ts where
aa = genCode t
Auch hier haben wir wieder einige Modellierungsentscheidungen getroffen, die man
sich klarmachen muß. Dies betrifft die Behandlung inkorrekt aufgebauter Gene, die auch

20 2. Modellierung
in der Natur gelegentlich vorkommen. Fehlt das Startcodon, wird kein Protein produziert.
Ist das Gen unvollständig, d.h. bricht es ohne Stopcodon ab, so ist ein unvollständiges
Proteinprodukt entstanden, das entsorgt werden muß. Im Modell ist dies so ausgedrückt:
• Fehlt das Startcodon, gibt es keine passende Rechenregel für ribosome, und die
Rechnung beginnt gar nicht erst.
• Ist das letzte Triplett unvollständig, bleibt die Rechnung in einer Formel der Art
triplets [a] oder triplets[a,b] stecken, für die wir keine Rechenregel vorgesehen
haben. Ein Fehlen des Stopcodons wird verziehen. Wer dies nicht will,
streicht die erste Regel für translate, so daß ohne Stopcodon die Rechnung am Ende
in translate [] steckenbleibt.
Eine frühere Entscheidung hat sich hier gelohnt: Da wir den Listentyp polymorph eingeführt
haben, können wir hier auch ganz nebenbei Listen von Codons, d.h. den Typ
[Codon] verwenden.
Bisher haben wir Vorgänge modelliert, die in der Natur selbst vorkommen. Zum Abschluß
nehmen wir den Standpunkt des Naturforschers ein. Heute liefern die großen
Sequenzierprojekte dank weitgehender Automatisierung eine Fülle von DNA-Sequenzen
immer mehr Organismen. Von einigen ist sogar bereits das komplette Genom bekannt,
etwa vom Koli-Bakterium (ca. 3 Millionen Basenpaare) oder der Bäckerhefe (ca. 14 Millionen
Basenpaare). Den Forscher interessiert nun unter anderem, welche Gene eine neue
DNA-Sequenz möglicherweise enthält. Sequenzabschnitte, die den Aufbau eines Gens haben,
nennt man ORFs (open reading frames). Ob es sich bei ihnen tatsächlich um Gene
handelt, hängt davon ab, ob sie jemals vom Ribosom als solche behandelt werden. Dies
kann man der Sequenz heute nicht ansehen. Wohl aber ist es interessant, in einer neuen
DNA-Sequenz nach allen ORFs zu suchen und ihre Übersetzung in hypothetische Proteine
vorzunehmen. Wir wollen also für unsere Kollegin aus der Molekularbiologie eine
Funktion definieren, die genau dieses tut.
Damit ist unsere Aufgabe so bestimmt: Wir gehen von einem DNA-Doppelstrang aus,
der zu untersuchen ist. Als Ergebnis möchten wir alle ORFs in übersetzter Form sehen, die
in dem Doppelstrang auftreten.
Wir wollen diese Aufgabe durch eine Funktion analyseORFs lösen. Schon beim Versuch,
den Typ dieser Funktion anzugeben, wird klar, daß die Aufgabe zwar halbwegs ausreichend,
aber keineswegs vollständig beschrieben ist.
Was genau bedeutet „alle ORFs“? Weder in der DNA, noch in unserem Modell liegt
eine feste Einteilung der Nukleotidsequenz in Codons vor. Das Auftreten einer Dreiergruppe
A,T,G definiert implizit die Lage der folgenden Codons. Ein einzelnes Nukleotid
kann so drei verschiedenen Leserastern angehören, in denen es jeweils als 1., 2. oder 3.
Element eines Codons interpretiert wird. Damit kann ein DNA-Abschnitt überlappende

2.4. Modellierung in der molekularen Genetik 21
ORFs enthalten. Das gleiche gilt für den Gegenstrang, der dabei in umgekehrter Richtung
abzulesen ist.
„Alle ORFs“ zu finden ist also etwas komplizierter als es zunächst erscheint. Das führt
zu der Frage, wie eigentlich das Ergebnis aussehen soll. Einfach eine Liste aller ORFs,
die vorkommen? Oder will man zu jedem ORF auch wissen, in welchem Leseraster auf
welchem Strang er liegt? Möchte man gar zusätzliche Informationen erhalten, wie etwa
Länge eines ORF und seine Lage relativ zum Anfang der DNA-Sequenz? Schließlich –
wir wissen ja was unsere Kollegin letzlich interessiert – könnte man die hypothetischen
Proteine noch mit einer Proteindatenbank abgleichen, um zu sehen, ob ein solches (oder
ein ähnliches) Protein an anderer Stelle bereits nachgewiesen wurde ...
Es ist immer ein gutes Entwurfsprinzip
• möglicherweise interessante Information, die während der Rechnung anfällt, auch
im Ergebnis sichtbar zu machen. Dies gilt hier für die Verteilung der ORFs auf die
Leseraster.
• die Funktionalität eines Entwurfs nicht zu überfrachten. Was gut und logisch einleuchtend
durch zwei getrennte Funktionen realisiert werden kann, wird auch getrennt.
Dadurch entstehen kleine Bausteine von überschaubarer Komplexität, die
möglicherweise auch in anderem Kontext wiederverwendbar sind.
Wir entscheiden, daß das Ergebnis eine Liste von 6 Listen übersetzter ORFs sein soll,
getrennt nach Leseraster. Wir halten diesen Beschluß durch die entsprechende Typdeklaration
fest.
analyzeORFs :: DNA_DoubleStrand -> [[Protein]]
Da ein Startcodon an beliebiger Stelle stehen kann, bilden wir zunächst 6 verschiedene
Leseraster, die dann alle nach ORFs durchsucht werden.
frames3 :: DNA -> [[Codon]]
frames3 x = if length x < 3 then [[],[],[]]
else [triplets x, triplets (tail x),
triplets (tail(tail x))] where
triplets :: [a] -> [(a,a,a)]
triplets [] = []
triplets [_] = []
triplets [_,_] = []
triplets (a:b:c:x) = (a,b,c):triplets x
findStartPositions :: [Codon] -> [[Codon]]
findStartPositions [] = []
findStartPositions (c:x) = if c == (A,T,G) then (c:x):findStartPositions x
else findStartPositions x

22 2. Modellierung
analyzeORFs (strain,antistrain)
= map (map translate) orfs where
sixframes = frames3 strain ++ frames3 (reverse antistrain)
orfs = map findStartPositions sixframes
Der polymorphe Listendatentyp wird hier in verschiedener Weise benutzt; das Ergebnis
z.B. ist eine Liste von Listen von Listen von Aminosäuren. Wir unterstellen Funktionen
(++) und reverse, die Listen aller Art verketten bzw. umkehren. Die Umkehrung des
Gegenstrangs ist notwendig, weil dieser am Ribosom in gegenläufiger Richtung gelesen
wird. Die Funktion map schließlich wendet eine Funktion f auf alle Elemente einer Liste
an, so daß z.B. gilt map f [x,y,z] = [f x, f y, f z].
Einige Beispiele:
dna_seq3 = dnaPolymerase [A,A,T,G,T,C,C,A,T,G,A,A,T,G,C]
dna_seq4 = dnaPolymerase [A,T,G,A,T,G,A,A,T,G,C,C,G,G,C,A,T,T,C,A,T,C,A,T]
analyzeORFs dna_seq3 ==>
[[],
[[Met, Ser, Met, Asn], [Met, Asn]],
[[Met]],
[[Met, Asp, Ile]],
[],
[]]
analyzeORFs dna_seq4 ==>
[[[Met, Met, Asn, Ala, Gly, Ile, His, His],
[Met, Asn, Ala, Gly, Ile, His, His]],
[[Met, Pro, Ala, Phe, Ile]],
[],
[[Met, Met, Asn, Ala, Gly, Ile, His, His],
[Met, Asn, Ala, Gly, Ile, His, His]],
[[Met, Pro, Ala, Phe, Ile]],
[]]
Daß bei dna_seq4 auf Strang und Gegenstrang die gleichen hypothetischen Proteine
gefunden werden, liegt am besonderen Aufbau dieser Beispielsequenz: Strang und reverser
Gegenstrang (in umgekehrter Leserichtung) sind gleich.

2.5. Anforderungen an Programmiersprachen 23
2.5. Anforderungen an Programmiersprachen
Aus der Sprache der Mathematik haben wir den Umgang mit Formeln übernommen. Dabei
zeigt sich gleich ein wichtiger Unterschied: Die „Sprache“ der Mathematik ist im wesentlichen
fertig – die meisten Anwender kommen ein Leben lang mit den einmal erlernten
Formeln und Begriffen – sagen wir einmal aus Arithmetik, Algebra und Analysis – aus.
Erweiterungen dieser Sprache, die Einführung neuer Begriffe und Notationen bleibt einer
kleinen Gemeinde von Forschern vorbehalten, die in dieser Hinsicht keinen Regeln unterliegen.
In der Informatik ist das Gegenteil der Fall. Modellierung bedeutet Schaffung
neuer Formelwelten. Jeder Programmierer führt neue Objekte (Typen) und Beziehungen
zwischen ihnen (Funktionen) ein. Wenn ein Formalismus ständig erweitert wird und trotzdem
allgemein verständlich und sogar durch den Computer ausführbar sein soll, dann muß
es einen festen Rahmen dafür geben, was man wie hinschreiben darf. Dies begründet die
besondere Rolle der Programmiersprachen in der Informatik. Ihre Syntax legt fest, wie
etwas aufgeschrieben wird. Ihre Semantik bestimmt, wie mit diesen Formeln zu rechnen
ist, sei es durch uns selbst, sei es durch den Computer. Eine präzise definierte Syntax und
Semantik ist die Mindestanforderung an eine Programmiersprache.
Anhand der vorangehenden Abschnitte können wir einige Beobachtungen dazu machen,
was eine Programmiersprache darüber hinaus leisten muss.
• Ein strenges, aber flexibles Typkonzept hält die Formelwelt in Ordnung. Streng bedeutet,
daß jeder Formel ein Typ zugeordnet wird und sich daher fast alle Programmierfehler
bereits als Typfehler bemerkbar machen. Flexibel heißt andererseits, daß
uns das Typkonzept nicht zwingen darf, die gleiche Operation mehrfach zu programmieren,
nur weil sich die Typen unwesentlich unterscheiden.
• Ein hierarchisch organisierter Namensraum erlaubt die Kontrolle über die Sichtbarkeit
von Namen. Definitionen können ihrerseits lokale Bezeichnungen einführen, die
nach außen hin nicht sichtbar sind. Die Funktion triplets haben wir zweimal und
leicht unterschiedlich definiert, jeweils als lokale Definition innerhalb der Definitionen
von ribosome und frames3. Ohne lokal beschränkte Sichtbarkeit könnte
man sich bei größeren Programmen vor Namenskonflikten nicht retten – man denke
allein an die vielfache Verwendung der Variablen „x“ . . . .
• Methoden zum Nachweis von Programmeigenschaften erlauben uns, die Übereinstimmung
des Modells mit wesentlichen Aspekten der modellierten Wirklichkeit zu
verifizieren. Auch die Korrektheit einzelner Funktionen sollte man einfach nachweisen
können, indem man algebraische Eigenschaften wie im Fall der exonuclease
benutzt.

24 2. Modellierung
• Ein hohes Abstraktionsniveau der Programmiersprache gewährleistet eine überschaubare
Beziehung zwischen Modell und Wirklichkeit. Wir wollen Rechenregeln formulieren,
die für uns nachvollziehbar sind. Schließlich müssen zuerst wir selbst unsere
Programme verstehen. Vom Computer nehmen wir einfach an, daß er damit klarkommt.
(Dafür zu sorgen ist natürlich die Aufgabe des Übersetzers für die jeweilige
Programmiersprache.) Sprachen auf geringem Abstraktionsniveau verlangen doppelten
Aufwand, weil die formale Beschreibung der Modellwelt und die Programmierung
auseinanderfallen.
Wir haben Haskell als Programmiersprache gewählt, weil es derzeit die obigen Kriterien
am besten erfüllt. Wir werden im Laufe der Vorlesung noch weitere Anforderungen an
Programmiersprachen kennenlernen, und nicht alle sehen Haskell als Sieger.

3. Eine einfache Programmiersprache
Ziele des Kapitels: Im Kapitel Modellierung haben wir uns darauf konzentriert, wie man
Objekte und Zusammenhänge der Realität durch Formeln und ihr Verhalten rechnerisch
nachbildet. Wir haben uns darauf verlassen, daß jeder mit Formeln rechnen kann, auch
wenn diese etwas anders aussehen als aus der Mathematik gewohnt. In diesem Kapi- Grit Garbo: Mit anderen Worten: ganz schön ungewohnt.
tel nehmen wir die umgekehrte Perspektive ein und betrachten näher, wie die Formeln
aussehen, mit denen wir rechnen (lassen) wollen. Mit anderen Worten: wir legen eine
Programmiersprache fest. Diese Sprache wollen wir möglichst einfach halten, da sie uns
nur als Vehikel dient, um über weitere Grundkonzepte der Informatik reden zu können.
Wir werden also nur einen Auschnitt aus der Sprache Haskell einführen.
Gliederung des Kapitels: Ein Haskell-Programm besteht aus einer Folge von Definitionen
und Deklarationen: Definiert werden Werte, meistens Funktionen, und neue Datentypen;
deklariert werden die Typen von Werten. Für Rechnungen spielen Deklarationen keine
Rolle; sie sind nur der „Ordnung halber“ da. Aber wie sagt man so schön: „Ordnung ist
das halbe Leben.“.
3.1. Datentypen
3.1.1. Datentypdefinitionen
Neue Typen und die dazugehörigen Werte werden mittels einer Datentypdefinition definiert.
Sie führen Daten-Konstruktoren (kurz Konstruktoren) ein, die unsere Formelwelt
bereichern. Beispiele aus Abschnitt 2.1 sind Musik und Instrument, die wir hier noch
einmal wiederholen:
data Instrument = Oboe
| HonkyTonkPiano
| Cello
| VoiceAahs
data Musik = Note Ton Dauer
| Pause Dauer
| Musik :*: Musik
| Musik :+: Musik

Übung 3.1 Definiere (&&), (||) und not.
26 3. Eine einfache Programmiersprache
| Instr Instrument Musik
| Tempo GanzeZahl Musik
Der Typ Instrument führt nur nullstellige Konstruktoren ein. Solche Typen nennt man
Aufzählungstypen. Der Typ Musik hat einen einstelligen Konstruktor (Pause) und fünf
zweistellige Konstruktoren (Note, (:*:), (:+:), Instr, Tempo). Diese Konstruktoren
nehmen wiederum Argumente eines bestimmten Typs, hier etwa Ton und Dauer für Note
und Instrument und Musik bei Instr.
Die Typen der Konstruktor-Argumente können auch Typparameter sein, wie wir das
schon beim Listentyp gesehen haben. Alle Typparameter werden als Argumente des Typnamens
auf der linken Seite der Definition angegeben. Die Datentypdefinition selbst wird
mit dem Schlüsselwort 1 data eingeleitet. Die allgemeine Form einer Datentypdefinition
hat somit die Gestalt
data T a1 . . . am = C1 t11 . . . t1n1
| . . .
| Cr tr1 . . . trnr
mit m 0, r 1 und ni 0. Im Falle m > 0 bezeichnet man den neuen Typ T auch
als Typkonstruktor, weil er in Analogie zu den Daten-Konstruktoren Typen als Argumente
nimmt und daraus Typausdrücke bildet. Allerdings treten diese nur in Typangaben auf und
sind keine Formeln, mit denen gerechnet wird.
Programmierhinweis: Die Namen von Typen bzw. Typkonstruktoren und Konstruktoren müssen
großgeschrieben werden (genauer: der erste Buchstabe groß, alle folgenden beliebig). Die Namen
von Werten bzw. Funktionen, Parametern und Typparametern müssen hingegen klein geschrieben
werden (genauer: der erste Buchstabe klein, alle folgenden beliebig). Jeder Name darf nur einmal
verwendet werden. Ausnahme: Für einen Typ und einen Konstruktor bzw. für eine Variable und
einen Typparameter darf der gleiche Name benutzt werden, da sich Werte und Typen „nicht in die
Quere kommen“.
Wir sehen uns nun einige Datentypen von allgemeiner Nützlichkeit an. Wir geben jeweils
die Typdefinition an, erläutern die Semantik des Typs, und gehen gegebenenfalls auf
spezielle Notationen ein.
Wahrheitswerte
data Bool = False | True -- vordefiniert
Die Konstruktoren False und True bezeichnen die Wahrheitswerte Falsch und Wahr.
Der Typ Bool ist ein Aufzählungstyp. Die Boole’schen Funktionen Konjunktion, Disjunktion
und Negation werden in Haskell mit (&&), (||) und not notiert.
1 Ein Schlüsselwort ist ein reservierter Name, der nicht für Funktionen etc. verwendet werden kann.

3.1. Datentypen 27
ifThenElse :: Bool -> a -> a -> a
ifThenElse True a a’ = a
ifThenElse False a a’ = a’
Für die Funktion ifThenElse gibt es als besondere Schreibweise die sogenannte Mixfix-
Notation, bei der der Funktionsname zwischen die Argumente eingestreut wird, etwa wie
in if x >= 0 then x else -x.
Ganze Zahlen
Ganze Zahlen sind vordefiniert als die Typen Integer und Int. Während Integer ganze
Zahlen beliebiger Größe enthält, sind die Zahlen im Typ Int auf einen bestimmten
Zahlenbereich begrenzt, der mindestens das Intervall [−2 29 , 2 29 − 1] umfaßt. Die Zahlen
vom Typ Int heißen auch Maschinenzahlen, während ihre Kolleginnen vom Typ Integer
mathematische Zahlen genannt werden. Auf letzteren kann mit beliebiger Genauigkeit gerechnet
werden, wobei man die Genauigkeit mit einer kleinen Geschwindigkeitseinbuße
erkauft. Auf ganzen Zahlen sind die üblichen arithmetische Operationen vordefiniert: Harry Hacker: Lieber schnell und falsch als langsam und genau.
(+), (-), (*), div, mod und (ˆ). Man beachte, daß es keine „echte Division“ auf den
ganzen Zahlen gibt: div bezeichnet die Division mit Rest. Es gilt der folgende Zusammenhang:
für alle ganzen Zahlen a und b.
Tupeltypen
data Pair a b = Pair a b
data Triple a b c = Triple a b c
(a ‘div‘ b) * b + (a ‘mod‘ b) == a (3.1)
Der Typkonstruktor Pair bildet Paare. Genauer: Pair a b umfaßt alle Paare, deren
erste Komponente vom Typ a und deren zweite vom Typ b ist. Entsprechend umfaßt
Triple a b c alle 3-Tupel. Für beide Typkonstruktoren gibt es äquivalente, vordefinierte
Typkonstruktoren: statt Pair a b schreibt man (a, b), statt Triple a b c schreibt
man (a, b, c). Nicht nur Paare und Tripel sind vordefiniert, sondern beliebige n-Tupel.
Bei Typkonstruktoren, die nur einen Datenkonstruktor haben, ist es üblich, für beide
den gleichen Namen zu verwenden: Pair 3 False ist ein Element vom Typ Pair
Integer Bool. Oder, in der Tupel-Notation: (3, False) ist ein Element vom Typ
(Integer, Bool). Die Konvention, für Werte und Typen die gleiche Notation zu verwenden,
ist am Anfang oft verwirrend. Hat man sich aber erst einmal daran gewöhnt, ist
es sehr bequem, da man sich nur eine Notation merken muß.
Für Paare sind Selektorfunktionen für das erste bzw. zweite Element vordefiniert.
Übung 3.2 Definiere Selektorfunktionen first, second und
third für 3-Tupel.

Lisa Lista: Kann man Folgen nicht auch anders modellieren? Wie
wär’s mit:
data List a = Empty
| Single a
| App (List a) (List a)
Der Konstruktor Empty ist wie gehabt die leere Liste; Single a
meint eine einelementige Liste und App hängt zwei Listen aneinander.
Harry Hacker: Witzig. Ich hab schon mal weitergeblättert: in
Abschnitt 3.4 wird was ähnliches eingeführt. Die nennen das
aber anders: Tree statt List, Nil statt Empty, Leaf statt
Single und Br statt App.
Prof. Paneau: Liebe StudentInnen, nun wollen wir uns nicht an
Namen stören: allein die Struktur zählt. Lisa greift etwas vor;
aber sie hat Recht: beide Darstellungen sind denkbar. Und: beide
haben ihre Vor- und Nachteile. Frau Lista, ich empfehle Ihnen,
(++), head, tail und reverse auf Ihrer Variante des
Datentyps List zu definieren.
Lisa Lista: Hey, (++) ist simpel:
(++) :: List a -> List a -> List a
(++) = App
Oh je, head und tail sind komplizierter.
Übung 3.3 Hilf Lisa bei der Definition von head und tail.
Lisa Lista: Die Definition von reverse ist elegant.
reverse’ :: List a -> List a
reverse’ Empty = Empty
reverse’ (Single a) = Single a
reverse’ (App l r) = App (reverse’ r) (reverse’ l)
28 3. Eine einfache Programmiersprache
fst :: (a,b) -> a -- vordefiniert
fst (a,b) = a
snd :: (a,b) -> b -- vordefiniert
snd (a,b) = b
Listen
data List a = Empty | Front a (List a)
Listen modellieren Folgen oder Sequenzen, also Sammlungen von Elementen, bei denen
die Reihenfolge der Elemente und die Häufigkeit eines Elements eine Rolle spielt. Dies unterscheidet
sie von Mengen, die sowohl von der Reihenfolge als auch von der Häufigkeit
abstrahieren.
Der Typ List a umfaßt alle Listen über dem Grundtyp a: Empty ist die leere Liste,
Front a x ist die Liste, deren erstes Element a ist, und deren restliche Elemente mit den
Elementen von x übereinstimmen; a wird als Kopfelement und x als Restliste bezeichnet.
Der Typ List a ist rekursiv definiert, da List a auch als Argumenttyp der Konstructors
Front auftritt. Rekursive Typen haben wir auch schon im Falle von Musik kennengelernt.
Neu ist hier nur, daß im Falle eines Typkonstruktors auch auf der rechten Seite
der Typparameter angegeben werden muß.
Auch für List a gibt es einen äquivalenten, vordefinierten Typ, den wir bereits aus
Abschnitt 2.4 kennen: Statt List a schreibt man [a], Empty wird zu [] und Front e x
zu e:x. Um Listen mit n Elementen aufzuschreiben, gibt es eine abkürzende Schreibweise:
Statt e1:(e2:· · ·(en:[])· · ·) schreibt man kurz [e1,e2,...,en].
Listen sind allgegenwärtig, und es gibt viele vordefinierte Funktionen. Der Operator
(++) hängt zwei Listen aneinander; head und tail greifen das Kopfelement bzw. die
Restliste heraus; reverse kehrt die Reihenfolge der Elemente um.
(++) :: [a] -> [a] -> [a]
[] ++ bs = bs
(a:as) ++ bs = a:(as++bs)
head :: [a] -> a
head (a:as) = a
tail :: [a] -> [a]
tail (a:as) = as
reverse :: [a] -> [a]
reverse [] = []
reverse (a:as)= reverse as ++ [a]

3.1. Datentypen 29
Der Typ Maybe
data Maybe a = Nothing | Just a -- vordefiniert
Der Typ Maybe a enthält die Elemente von Typ a (in der Form Just a) und zusätzlich
das Element Nothing. Oft wird Maybe zur Fehlerindikation und Fehlerbehandlung eingesetzt:
Nothing zeigt an, daß eine Operation nicht erfolgreich war; Just e zeigt an, daß
die Operation erfolgreich mit dem Resultat e abgeschlossen worden ist. Auch Maybe a
ist vordefiniert. Wie List a und Pair a b ist Maybe a ein parametrisierter Typ, ein
Typkonstruktor.
Als Beispiel nehmen wir an, wir wollen das kleinste Element einer Liste von Zahlen
bestimmen. Bei einer nicht-leeren Liste ist dies klar:
minimum1 :: [Integer] -> Integer
minimum1 [a] = a
minimum1 (a:as) = min a (minimum1 as)
Die Funktion minimum1 ist für leere Listen nicht definiert. Will man auch den Fall leerer
Listen handhaben, muß man die Funktion etwas allgemeiner definieren:
minimum0 :: [Integer] -> Maybe Integer
minimum0 [] = Nothing
minimum0 (a:as) = Just (minimum1 (a:as))
Wenn man so will, spielt Nothing hier die Rolle von +∞, dem neutralen Element von
min.
Zeichen und Zeichenketten
data Char = ... | ’0’ | ’1’ ... -- Pseudo-Haskell
| ... | ’A’ | ’B’ ...
| ... | ’a’ | ’b’ ...
type String = [Char]
Der Typ Char umfaßt die Zeichen des ASCII-Alphabets. Die Zeichen werden in Apostrophe
gesetzt, um sie von den sonst im Programm verwendeten Bezeichnungen zu unterscheiden.
Der Datentyp String beinhaltetet Zeichenketten, auch Texte genannt. Er ist
eine Spezialisierung des polymorphen Listentyps: Zeichenketten sind Listen mit Elementtyp
Char. Er führt keine neuen Konstruktoren ein, sondern wird als Typsynonym definiert.
(Mehr zu Typsynonymen findet man in Abschnitt 3.1.2.) Da Zeichenketten häufig verwendet
werden, gibt es eine bequeme Notation: statt der Liste [’M’,’a’,’r’,’v’,’i’,
’n’] schreibt man "Marvin", statt [] einfach "". Auf Zeichenketten sind natürlich alle
Lisa Lista: Diese Definition ist nicht geheuer. Schließlich kann
man [a] ebensogut als a:[] schreiben. Welche Gleichung gilt
dann? Die zweite Gleichung führt zu der verbotenen Anwendung
minimum1 [].
Lisa Lista: Hmm — dann muß [] den Typ [a] haben, aber ""
den Typ String.

30 3. Eine einfache Programmiersprache
Listenoperationen anwendbar, wie (++) oder reverse.
Programmierhinweis: Ein doppelter Anführungsstrich beendet eine Zeichenkette. Damit stellt sich
die Frage, wie man einen Anführungsstrich in einer Zeichenkette unterbringt: wie schreibt man
[’"’, ’a’, ’"’] kurz? Zu diesem Zweck gibt es sogenannte Ersatzdarstellungen, die mit einem
Backslash „\“ eingeleitet werden: "\"a\"". Den gleichen Trick verwendet man, um einen einfachen
Anführungsstrich als Zeichen zu schreiben: ’\’’. Da der Backslash nun seinerseits eine Sonderrolle
einnimmt, muß auch er mit einer Ersatzdarstellung notiert werden: "\\". Der Haskell-Report
führt in §2.5 alle Ersatzdarstellungen auf. Die Funktion isSpace illustriert die Verwendung von
Ersatzdarstellungen; sie überprüft, ob ein Zeichen ein Leerzeichen ist.
isSpace :: Char -> Bool
isSpace c = c == ’ ’ || c == ’\t’ || c == ’\n’ ||
c == ’\r’ || c == ’\f’ || c == ’\v’
3.1.2. Typsynonyme
Typsynonyme bereichern die Formelwelt nicht. Manchmal macht es jedoch Sinn, einem
bestimmten Typ einen zweiten Namen zu geben. Oft ist dies nur bequem im Sinne einer
Abkürzung. Manchmal will man andeuten, daß man die Objekte dieses Typs in einer
besonderen, eingeschränkten Weise verwendet. Verschiedene Typsynonyme haben wir
schon gesehen (Ton, Dauer, DNA, Protein, String). Ein weiteres Beispiel zeigt zugleich
Nutzen und Gefahr: Stellen wir uns vor, wir wollen in einem Programm Listen (Typ [a])
verwenden, die aber stets geordnet sein sollen. Wir können ein Typsynonym einführen,
das diese Absicht ausdrückt:
type OrdList a = [a]
merge :: OrdList a -> OrdList a -> OrdList a
Im Typ der Funktion merge können wir damit ausdrücken, daß diese Funktion zwei
geordnete Listen verknüpft und eine geordnete Liste als Ergebnis hat. Wir denken dabei
an ein Pedant der (++)-Funktion auf geordneten Listen. So weit so gut — unsere Absicht
haben wir damit ausgedrückt. Ob wir unser Ziel auch erreichen, liegt jedoch ausschließlich
daran, wie wir merge programmieren. Was die Typen betrifft, sind Ordlist a und [a]
gleich, so daß von daher niemand garantiert, daß das Ergebnis von merge tatsächlich
geordnet ist. In diesem Sinn können Typsynonyme auch einmal falsche Sicherheit stiften.
3.1.3. Typdeklarationen, Typprüfung und Typinferenz
Wenn wir neue Bezeichner einführen, werden wir stets ihre Typen deklarieren. Dies geschieht
in der Form, die wir in Abschnitt 2.2 kennengelernt haben. Die Deklaration
x :: τ besagt, daß wir für den Bezeichner x den Typ τ vorsehen. Streng genommen

3.1. Datentypen 31
müssen die Typen nicht deklariert werden, da sie aus der Definition der Bezeichner abgeleitet
werden können. Diesen Vorgang nennt man Typinferenz. Es ist nützlich dieses
Verfahren zumindest in groben Zügen zu kennen. Denn: viele Programmierfehler äußern
sich als Tippfehler; um dem Fehler auf die Schliche zu kommen, muß man die Fehlermeldung
verstehen. Betrachten wir die Definition der vordefinierten Funktion map:
map f [] = [] -- vordefiniert
map f (a:as) = f a : map f as
Wir leiten in mehreren Schritten einen immer genaueren Typ für map ab. Dabei sind c,
d, e etc Typvariablen, die zunächst frei gewählt sind, dann aber durch Betrachtung der
Definition von map weiter spezifiziert werden.
Beobachtungen über map Typ von map
map hat zwei Argumente. c -> d -> e
Das Ergebnis ist eine Liste. c -> d -> [b]
Das zweite Argument ist eine Liste. c -> [a] -> [b]
Das erste Argument ist eine Funktion, (f -> g) -> [a] -> [b]
die Argumente vom Typ a erhält, (a -> g) -> [a] -> [b]
und Elemente der Ergebnisliste vom Typ b liefert. (a -> b) -> [a] -> [b]
Die gewonnene Typaussage läßt sich etwas wortreich so formulieren: map ist eine Funktion,
die auf beliebige Funktionen f und Listen as anwendbar ist, vorausgesetzt der Argumenttyp
von f stimmt mit dem Elementtyp von as überein. Das Ergebnis ist dann eine
Liste von Elementen, die den Ergebnistyp von f haben. Zum Glück kann man dies auch
kürzer sagen, eben
map :: (a -> b) -> [a] -> [b]
Wir haben darauf geachtet, daß der Typ von map nicht unnötig eingeschränkt wird. Hätten
wir grundlos den gleichen Typ für Argument- und Ergebnisliste angenommen, etwa [a],
hätten wir insgesamt den spezifischeren Typ (a -> a) -> [a] -> [a] erhalten. Bei
der Typinferenz wird immer der allgemeinste Typ hergeleitet, um den Einsatzbereich einer
Funktion nicht unnötig zu verengen.
Der Typ von map ist polymorph, da er Typparameter enthält. Wird map auf konkrete
Argumente angewandt, spezialisiert sich der Typ in der Anwendung.
Harry Hacker: Muß ich mich wirklich mit diesem Typenwahn
herumschlagen? Korrekte Programme brauchen keine Typen. Jede
Funktion angewandt auf’s richtige Argument — da kann ja
gar nichts schiefgehen.
Lisa Lista: Mag schon sein, Harry. Aber wie kommst Du zu den
korrekten Programmen?

Harry Hacker: Also enthält Eq alle Typen. Warum dieser Aufwand?
Lisa Lista: Hmm — wie steht’s mit Funktionen? Kann man
f == g für zwei Funktionen überhaupt implementieren? Und
was ist mit Typen, die Funktionen enthalten?
32 3. Eine einfache Programmiersprache
Spezialisierung von
Anwendung von map a b
map c’ [1/4, 1/8, 1/8, 1/4] Dauer Musik
map (transponiere 5)
[cDurTonika, cDurSkala, bruderJakob] Musik Musik
map genCode cs Codon AminoAcid
map (map translate) orfs zwei Auftreten verschiedenen Typs!
inneres Auftreten Codon Protein
äußeres Auftreten [[Codon]] [Protein]
Der Haskell-Übersetzer führt stets die Typinferenz durch. Dies ist zugleich die Typ-Überprüfung:
Stößt die Typinferenz auf einen Widerspruch, so daß sich kein Typ ableiten läßt,
liegt eine nicht wohl-getypte Formel, kurz ein Typfehler vor. Daneben kann es geschehen,
daß der abgeleitete Typ spezieller ist als der deklarierte Typ. Auch in diesem Fall erfolgt
eine Fehlermeldung des Übersetzers, die man vermeiden kann, wenn man die Typdeklaration
löscht. Wesentlich klüger ist es allerdings in einem solchen Fall, noch einmal darüber
nachzudenken, welche Funktion man eigentlich programmieren wollte. Der umgekehrte
Fall ist erlaubt: der abgeleitete Typ ist allgemeiner als der deklarierte. In diesem Fall wird
die Anwendbarkeit der Funktion bewußt oder vielleicht unbewußt eingeschränkt.
3.1.4. Typklassen und Typkontexte
Typklassen und Typkontexte werden hier nur kurz besprochen, insoweit es für die nächsten
Kapitel erforderlich ist. Wir werden sie im Kapitel über Typabstraktion genauer kennen
lernen.
Typklassen fassen Typen zusammen, die gewisse Operationen gemeinsam haben. Hier
soll nur gesagt werden, daß es u. a. vordefinierte Typklassen Eq, Ord, Num, Integral
und Show gibt. Die Typklasse
• Eq enthält alle Typen, deren Elemente man auf Gleichheit testen kann, und definiert
die folgenden Funktionen:
(==) :: (Eq a) => a -> a -> Bool
(/=) :: (Eq a) => a -> a -> Bool
• Ord enthält alle Typen, deren Elemente man bezüglich einer Ordnungsrelation vergleichen
kann, und definiert u.a. die folgenden Funktionen:
() :: (Ord a) => a -> a -> Bool
max, min :: (Ord a) => a -> a -> a

3.1. Datentypen 33
• Num enthält alle numerischen Typen und definiert die grundlegenden arithmetischen
Operationen.
(+), (-), (*) :: (Num a) => a -> a -> a
negate :: (Num a) => a -> a
Die Funktion negate entspricht dem unären Minus.
• Integral enthält die ganzzahligen Typen Int und Integer und definiert u.a. die
folgenden Funktionen:
div, mod :: (Integral a) => a -> a -> a
even, odd :: (Integral a) => a -> Bool
• Show enthält alle Typen, die eine externe Darstellung als Zeichenketten haben. Die
Funktion show liefert diese Darstellung.
show :: (Show a) => a -> String
Für alle vordefinierten Typen ist natürlich bereits festgelegt, welchen Typklassen sie angehören.
Bei neu deklarierten Typen kann man dies für die Klassen Eq, Ord und Show
erreichen, indem der Typdefinition die Klausel deriving (Eq, Ord, Show) hinzugefügt
wird. Dies bewirkt, daß automatisch die oben genannten Operationen auch auf dem
neuen Datentyp definiert sind.
Typkontexte schränken den Polymorphismus von Funktionen ein: Die Schreibweise
(K a) => ... besagt, daß der Typparameter a auf Typen eingeschränkt ist, die der Klasse
K angehören. So haben wir zum Beispiel in der Definition der Funktion minimum1 vorausgesetzt,
daß die Listenelemente mittels min verglichen werden können. Da min den
Typ (Ord a) => a -> a - > a hat, müssen die verglichenen Listenelemente der Typklasse
Ord angehören. Dies ist der Fall: der Typ Integer gehört der Typklasse Ord an.
Wollen wir eine polymorphe minimum-Funktion definieren, so geschieht dies analog zu
minimum1 unter Benutzung eines Typkontextes (Ord a) =>.
minimum :: (Ord a) => [a] -> a -- vordefiniert
minimum [a] = a
minimum (a:as) = min a (minimum as)
Hier erkennt man die enorme praktische Bedeutung der Typklassen: Die obige Definition
definiert minimum auf allen Listen geeigneten Typs. Speziellere Versionen wie unser
minimum1 sind überflüssig.

Lisa Lista: Hmm — monotonie ist doch identisch mit dem
Funktionsaufruf adInfinitum (c’ (1/1)). Aber auch die
rekursive Definition von adInfinitum ist ungewöhnlich.
34 3. Eine einfache Programmiersprache
3.2. Wertdefinitionen
3.2.1. Muster- und Funktionsbindungen
Musterbindungen
Mit Hilfe einer oder mehrerer Gleichungen definieren wir einen oder mehrere Bezeichner.
Im einfachsten Fall hat die Gleichung die Form x = e, wobei x der definierte Bezeichner
ist und e der definierende Ausdruck. Gleichungen dieser Form heißen auch Variablenbindungen,
da die Variable an den Wert der rechten Seite gebunden wird.
theFinalAnswer :: Integer
theFinalAnswer = 42
aShortList :: [Integer]
aShortList = [1,2,3]
helloWorld :: String
helloWorld = "Hello World"
Das Gleichheitszeichen drückt aus, daß die linke Seite und die rechte Seite per definitionem
gleich sind; somit können wir theFinalAnswer stets durch 42 ersetzen und
umgekehrt, ohne dabei die Bedeutung des Programms zu verändern. Weiterhin tut es
einer Definition keinen Abbruch, wenn der Ausdruck auf der rechten Seite erst noch auszurechnen
ist:
theFinalAnswer’ :: Integer
theFinalAnswer’ = 6*7
aShortList’ :: [Integer]
aShortList’ = reverse ([3]++[2,1])
helloWorld’ :: String
helloWorld’ = "Hello" ++ " " ++ "World"
Diese Bezeichner haben den gleichen Wert wie die zuvor definierten. Interessantere
Beispiele für Variablenbindungen sind cDurSkala und bruderJakob aus Kapitel 2.
Bezeichner können auch rekursiv definiert sein. Von Funktionen sind wir das mittlerweile
gewohnt; neu und überraschend ist vielleicht, daß Elemente beliebiger Datentypen
rekursiv definiert sein können.
monotonie :: Musik
monotonie = c’ (1/1) :*: monotonie

3.2. Wertdefinitionen 35
Was ist an dieser Definition ungewöhnlich? Genau — das zu definierende Objekt wird
durch sich selbst erklärt. Daß eine solche Definition nicht sinnlos ist, kann man sich auf
zwei Arten klarmachen. Beginnt man einfach, das Musikstück monotonie mit Hilfe seiner
Definition auszurechnen, sieht man schnell, daß das (potentiell) unendliche Stück
c’ (1/1) :*: c’ (1/1) :*: · · · entsteht. Fragt man sich, ob es ein Musikstück gibt,
das die Definitionsgleichung von monotonie erfüllt, kommt man (nach einigen Fehlversuchen
mit endlichen Stücken) ebenfalls auf die Antwort c’ (1/1) :*: c’ (1/1) :*:
· · ·. Unendliche Objekte in der Art von monotonie sind kein Problem in Haskell, man
darf sie nur nie ganz ausrechnen (lassen).
Auf der linken Seite einer Gleichung darf auch ein sogenanntes Muster stehen. In diesem
Fall spricht man von einer Musterbindung; diese sind von der Form p = e, wobei p ein
Muster und e ein Ausdruck ist. Ein Muster ist eine Formel, die ausschließlich aus Variablen
und Konstruktoren aufgebaut ist: (a, b), a : a’ : as oder m1 :*: m2 sind Beispiele
für Muster. In einem Muster darf keine Variable mehrfach enthalten sein: (a, a) ist
kein gültiges Muster. Musterbindungen treten in erster Linie im Zusammenhang mit lokalen
Definitionen auf, die wir in Abschnitt 3.2.3 kennenlernen werden. Aus diesem Grund
verzichten wir hier auf die Angabe von Beispielen.
Funktionsbindungen
Datentypen erlauben uns, Formeln zu bilden, Funktionen erlauben uns, mit ihnen zu rechnen.
Eine Funktion wird durch eine oder mehrere Gleichungen definiert. Generell gilt, daß
diese Gleichungen unmittelbar aufeinander folgen müssen, und nicht etwa im Programm
verteilt stehen dürfen.
Mehrfache Gleichungen dienen einer Fallunterscheidung über die Argumente. Im einfachsten
und häufigsten Fall wird diese Unterscheidung anhand der Konstruktoren getroffen,
aus denen die Argumente aufgebaut sind. Entsprechend dem Typ der Argumente gibt
es im einfachsten Fall genau eine Gleichung pro Konstruktor. Fast alle bisherigen Definitionen
haben wir so geschrieben. Hier ein weiteres Beispiel:
length :: [a] -> Int -- vordefiniert
length [] = 0
length (a:as) = 1 + length as
Der Typ [a] hat die zwei Konstruktoren [] und (:), die gerade die beiden relevanten
Fälle unterscheiden helfen. Analog in der Definition von transponiere in Kapitel 2: Der
Typ Musik hat sechs Konstruktoren, entsprechend werden sechs Gleichungen geschrieben.

Übung 3.4 Definiere member ohne Wächter unter Verwendung
der Boole’schen Funktionen (&&) und (||).
36 3. Eine einfache Programmiersprache
Der allgemeine Fall ist etwas flexibler: Die Definition einer n-stelligen Funktion f durch
Mustergleichungen geschieht durch k 1 Gleichungen der Form
f p11 . . . p1n = e1
. . . = . . .
f pk1 . . . pkn = ek
Dabei sind die pij Muster und die ei Ausdrücke. Es gilt die Einschränkung, daß die Muster
einer Gleichung keine Variable mehrfach enthalten dürfen. Die Ausdrücke ei dürfen
jeweils die Variablen aus den Mustern pi1, . . . , pin enthalten. Da Muster beliebig kompliziert
aufgebaut sein können, kann es mehr Gleichungen als Konstruktoren geben.
3.2.2. Bewachte Gleichungen
Nicht immer lassen sich die relevanten Fälle allein anhand von Mustern unterscheiden.
Fallunterscheidungen können aus diesem Grund auch mit Hilfe von sogenannten Wächtern
erfolgen. Die Funktion dropSpaces entfernt führende Leerzeichen aus einer Zeichenkette.
dropSpaces :: String -> String
dropSpaces [] = []
dropSpaces (c:cs)
| isSpace c = dropSpaces cs
| otherwise = c : dropSpaces cs
Der Boole’sche Ausdruck nach dem senkrechten Strich heißt Wächter, da er über die
Anwendung der jeweiligen Gleichung wacht. Der Ausdruck otherwise ist ein Synonym
für True und tritt — wenn überhaupt — als letzter Wächter auf. Damit ist schon gesagt,
daß die Anzahl der Wächter nicht auf zwei beschränkt ist.
Die Funktion squeeze komprimiert Wortzwischenräume auf ein einzelnes Leerzeichen.
squeeze :: String -> String
squeeze [] = []
squeeze (c:c’:cs)
| isSpace c && isSpace c’ = squeeze (c’:cs)
squeeze (c:cs) = c : squeeze cs
Die zweite Gleichung behandelt den Fall, daß die Zeichenkette mindestens zwei Elemente
umfaßt und beide Zeichen als Leerzeichen qualifizieren. Ist dies gegeben, so wird
ein Leerzeichen entfernt.
Drei Wächter kommen bei der Definition von member zum Einsatz: member a bs
überprüft, ob das Element a in der aufsteigend geordneten Liste bs enthalten ist.

3.2. Wertdefinitionen 37
member :: (Ord a) => a -> OrdList a -> Bool
member a [] = False
member a (b:bs)
| a < b = False
| a == b = True
| a > b = member a bs
Ist das gesuchte Element a kleiner als der Listenkopf, kann die Suche unmittelbar abgebrochen
werden.
3.2.3. Gleichungen mit lokalen Definitionen
Rechnen ist selten eine geradlinige Angelegenheit: Man führt Hilfsrechnungen durch,
stellt Zwischenresultate auf, verwendet diese in weiteren Zwischenrechnungen usw. Es
ist nur natürlich, dieses Vorgehen auch in unserer Programmiersprache zu ermöglichen.
Der Zutaten bedarf es nicht vieler: Eine oder mehrere Formeln, die zwischengerechnet
werden, einen oder mehrere Namen für die Ergebnisse der Rechnungen und eine Formel,
in der die Namen verwendet werden.
Das folgende Programm, das die n-te Potenz einer ganzen Zahl x berechnet, illustriert
die Verwendung einer lokalen Definition.
power :: (Num a, Integral b) => a -> b -> a
power x n
| n == 0 = 1
| n ‘mod‘ 2 == 0 = y
| otherwise = y*x
where y = power (x*x) (n ‘div‘ 2)
Nach dem Schlüsselwort where werden die Hilfsdefinitionen angegeben (hier ist es
nur eine). Mit Ausnahme von Typdefinitionen können alle Arten von Definitionen und
Deklarationen, die wir bisher kennengelernt haben, auch lokal erfolgen. Die Funktion
splitWord, die ein Wort von einer Zeichenkette abtrennt, illustriert die Verwendung
von lokalen Musterbindungen.
splitWord :: String -> (String, String)
splitWord [] = ([],[])
splitWord (c:cs)
| isSpace c = ([], c:cs)
| otherwise = (c:w, cs’)
where (w, cs’) = splitWord cs
Harry Hacker: Warum ist die Definition so kompliziert? Wie
wär’s mit
pow :: (Num a) => a -> Integer -> a
pow x n
| n == 0 = 1
| otherwise = x * pow x (n-1)
Lisa Lista: Hmm — rechne mal pow 2 1024 aus.
Harry Hacker: Ja, ja, Du hast wieder mal recht. Aber daß die
Definition von power korrekt ist, sehe ich noch nicht.
Grit Garbo: Typisch, die Informatiker kennen die einfachsten
Dinge nicht. Hier handelt es sich um eine triviale Anwendung
der Potenzgesetze:
x n = x 2(n div 2)+n mod 2 = (x 2 ) n div 2 n mod 2
x

Harry Hacker: Wer so programmiert, ist selber schuld!
38 3. Eine einfache Programmiersprache
Auf der linken Seite der lokalen Definition steht ein Muster, woran das Ergebnis der
rechten Seite gebunden wird. Auf diese Weise werden mehrere Variablen gleichzeitig definiert.
Musterbindungen treten typischerweise bei der Definition rekursiver Funktionen
auf, die Paare oder n-Tupel zum Ergebnis haben.
Gültigkeits- oder Sichtbarkeitsbereiche
Die where-Klausel führt neue Namen ein, genau wie andere definierende Gleichungen.
Diese neuen Namen haben einen lokalen Bereich, in dem sie benutzt werden können.
Diesen Bereich nennt man Gültigkeits- oder Sichtbarkeitsbereich. Er erstreckt sich auf die
rechte Seite der Gleichung, mit der die where-Klausel assoziiert ist, und auf die rechten
Seiten aller Gleichungen innerhalb der where-Klausel, einschließlich darin verschachtelter
where-Klauseln. Führt eine lokale Definition einen neuen Namen ein, der im umgebenden
Kontext bereits definiert ist, so gilt innerhalb des lokalen Sichtbarkeitsbereichs die
lokale Definition. Man sagt, die globale Definition wird verschattet. Schauen wir uns ein
(Negativ-) Beispiel an:
f :: Int -> Int -- Negativ-Beispiel
f x = f (x+x)
where x = 1
f x = x
Der Bezeichner f wird zweimal definiert, die Variable x wird gar an drei Stellen eingeführt:
zweimal als Parameter und einmal in der lokalen Definition x = 1. Die inneren
Definitionen verschatten die äußeren, so daß f zu f1 mit
f1 :: Int -> Int
f1 x1 = f2 (x2+x2)
where x2 = 1
f2 x3 = x3
äquivalent ist. Man sieht, daß die Definition der Funktion f insbesondere nicht rekursiv
ist, da die lokale Definition bereits für den Ausdruck f (x + x) sichtbar ist und das
global definierte f verschattet. Da Programme in der Art von f schwer zu lesen und
zu verstehen sind, empfehlen wir, in lokalen Definitionen grundsätzlich andere („neue“)
Bezeichner zu verwenden.
Abseitsregel
Eine Frage ist noch offen: Es ist klar, daß der lokale Sichtbarkeitsbereich der where-Klausel
nach dem Schlüsselwort where beginnt. Aber wo endet er eigentlich? Woher wissen wir,

3.2. Wertdefinitionen 39
daß die Gleichung f x = x Bestandteil der where-Klausel ist, und nicht etwa eine zweite
(wenn auch überflüssige) Gleichung für das global definierte f darstellt?
Antwort: der Übersetzer erkennt das Ende der where-Klausel am Layout des Programmtextes.
Wir haben die lokale Definition entsprechend dem Grad ihrer Schachtelung
eingerückt. Diese Formatierung erleichtert es, ein Programm zu lesen und zu verstehen.
Der Übersetzer macht sich diese Konvention zunutze, um das Ende einer lokalen Definition
zu erkennen. Es gilt die folgende sogenannte Abseitsregel:
• Das erste Zeichen der Definition unmittelbar nach dem where bestimmt die Einrücktiefe
des neu eröffneten Definitionsblocks.
• Zeilen, die weiter als bis zu dieser Position eingerückt sind, gelten als Fortsetzungen
einer begonnenen lokalen Definition.
• Zeilen auf gleicher Einrücktiefe beginnen eine neue Definition im lokalen Block.
• Die erste geringer eingerückte Zeile beendet den lokalen Block.
Lisa Lista: Die Folgen dieser anderen Interpretation kommen
mir etwas unheimlich vor!
Harry Hacker: Ist das noch zu fassen — die Bedeutung des
Programms ist vom Layout abhängig! Das ist ja wie in alten
FORTRAN-Tagen! Noch dazu jede Definition auf einer neuen
Zeile. Da werden die Programme viel länger als nötig.
Die Abseitsregel erlaubt die Einsparung von Abgrenzungssymbolen wie begin, end oder
geschweiften Klammern und Semikola, die man in anderen Programmiersprachen verwenden
muß. Außerdem trägt sie dazu bei, daß Programme verschiedener Autoren in
einem relativ einheitlichen Stil erscheinen. Trotz dieser Vorzüge ist die Verwendung der
Abseitsregel optional — es gibt sie doch, die formatfreie Schreibweise: Eingeschlossen in Harry Hacker: Na also, sagt es doch gleich!
geschweifte Klammern und getrennt durch Semikolons (also in der Form {d1; ...; dn})
können die Definitionen eines Blocks beliebig auf eine Seite drapiert werden. Ein Fall, wo
dies sinnvoll ist, ist eine lange Reihe sehr kurzer Definitionen.
Die allgemeine Form von Gleichungen
Jetzt haben wir alle Konstrukte kennengelernt, um die allgemeine Form einer Funktionsbindung
einzuführen: Eine n-stellige Funktion f mit n 1 kann durch k Gleichungen
definiert werden:
f p11 . . . p1n m1
. . .
f pk1 . . . pkn mk
Die pij sind beliebige Muster und die mi nehmen wahlweise eine der beiden folgenden
Formen an:
= e where { d1; . . . ;dp }

40 3. Eine einfache Programmiersprache
oder
| g1 = e1
. . .
| gq = eq
where { d1; . . . ;dp }
Der where-Teil kann jeweils auch entfallen. Bezüglich der Sichtbarkeit der Bezeichner gilt
folgendes: Die in den di eingeführten Bezeichner sind in dem gesamten Block sichtbar,
d.h. in den Wächtern gi, in den rechten Seiten ei und in den Definitionen di selbst. Den
gleichen Sichtbartkeisbereich haben auch die Variablen, die in den Mustern auf der linken
Seite eingeführt werden: die in pi1, . . . , pin enthaltenen Variablen sind in mi sichtbar
(nicht aber in den anderen Gleichungen).
Musterbindungen haben die allgemeine Form p m, wobei p ein Muster ist und m wie im
Fall von Funktionsbindungen aussieht. Im Unterschied zu Funktionsbindungen definiert
eine Musterbindung unter Umständen gleichzeitig mehrere Bezeichner.
3.2.4. Das Rechnen mit Gleichungen
Kommen wir zum Rechnen. Einen Teil seiner Schulzeit verbringt man damit, Rechnen zu
lernen: Ist zum Beispiel die Funktion q gegeben durch
q :: (Num a) => a -> a
q x = 3*xˆ2 + 1
dann wird man den Ausdruck q 2 - 10 unter Zuhilfenahme der Rechenregeln für die
Grundrechenarten ohne große Schwierigkeiten zu 3 ausrechnen:
q 2 - 10
⇒ (3 * 2ˆ2 + 1) - 10 (Definition von q)
⇒ (3 * 4 + 1) - 10 (Definition von (ˆ))
⇒ (12 + 1) - 10 (Definition von (*))
⇒ 13 - 10 (Definition von (+))
⇒ 3 (Definition von (-))
Das Rechnen in oder mit Haskell funktioniert nach dem gleichen Prinzip: Ein Ausdruck
wird relativ zu einer Menge von Definitionen zu einem Wert ausgerechnet. Die Notation
e ⇒ v verwenden wir, um dies zu formalisieren. Beachte: das Zeichen „⇒“ ist kein Bestandteil
der Programmiersprache, sondern dient dazu, über die Programmiersprache zu
reden.
Wir unterscheiden zwei Formen des Rechnens: Da ist einmal das Ausrechnen eines
Ausdrucks, seine Auswertung. Dabei werden die Gleichungen stets von links nach rechts

3.2. Wertdefinitionen 41
angewandt: Tritt irgendwo in dem Ausdruck eine linke Seite einer Gleichung auf, so kann
sie durch die rechte Seite ersetzt werden (wobei die Variablen aus den Mustern der linken
Seite an Unterausdrücke gebunden werden, die in die rechte Seite einzusetzen sind).
Dabei ist zu beachten: Wird ein Bezeichner durch mehrere Gleichungen definiert, so muß
die erste (im Sinne der Aufschreibung) passende Gleichung verwendet werden. Die Gleichung
f p1 . . . pn | g = e paßt auf eine Anwendung f a1 . . . an, wenn die Argumente a1,
. . . , an aus den Konstruktoren aufgebaut sind, die durch die Muster p1, . . . pn vorgegeben
sind und der Wächter g zu True auswertet. Die Rechnung endet, wenn keine Gleichung
anwendbar ist. Man sagt dann, der Ausdruck ist in Normalform. Ein berühmter Satz von
Church und Rosser besagt, daß die Normalform, wenn sie existiert, eindeutig ist. Wir können
also den Wert eines Ausdrucks mit seiner Normalform identifizieren. Hat ein Ausdruck
keine Normalform — d. h. die Rechnung endet nie — so ist sein Wert undefiniert. Auswertung
eines Ausdrucks auf Normalform — das ist Rechnen lassen in einer funktionalen
Programmiersprache.
Die zweite Form des Rechnens tritt auf, wenn wir selbst nicht nur Werte ausrechnen,
sondern über Programme nachdenken. Uns steht es dabei frei, Mustergleichungen auch
von rechts nach links anzuwenden, oder mit Gleichungen zu rechnen, die allgemeine
Programmeigenschaften beschrieben und keine Mustergleichungen sind. Mehr dazu im
Kapitel 4.
3.2.5. Vollständige und disjunkte Muster
Im Allgemeinen achtet man darauf, daß die Mustergleichungen vollständig und disjunkt sind. Vollständig
heißt, daß die Funktion für alle möglichen Fälle definiert ist. Disjunkt heißt, daß die Muster
so gewählt sind, dß für jeden konkreten Satz von Argumenten nur eine Gleichung paßt. Die
Definition von unique, das aufeinanderfolgende Duplikate aus einer Liste entfernt, erfüllt diese
Forderungen.
unique [] = []
unique [a] = [a]
unique (a:(b:z)) = if a == b then unique (b:z)
else a : unique (b:z)
Hier unterscheiden die Muster den Fall der null-, ein- oder mehrelementigen Liste.
Wir betrachten nun Situationen, in der die Forderungen Vollständigkeit und Disjunktheit nicht
erfüllt werden können:
Nehmen wir die Funktion head mit head [a1,...,an] = a1. Ist die Liste leer, ist das Funktionsergebnis
nicht definiert. Was bedeutet dies für das Rechnen? Nun, ist man gezwungen head []
auszurechnen, so bleibt einem nicht anderes übrig als abzubrechen und aufzugeben. Das Beste,
was man als Programmiererin machen kann, ist den Abbruch der Rechnung mit einer Meldung zu
garnieren, die die Ursachen des Abbruchs beschreibt. Diesem Zweck dient die Funktion error.

42 3. Eine einfache Programmiersprache
head :: [a] -> a -- vordefiniert
head [] = error "head of empty list"
head (a:x) = a
Diese Definition von head ist also eine Verbesserung der früher gegebenen, die nun einen vollständigen
Satz von Mustergleichungen aufweist. Ähnlich kann man im Falle der Funktion tail
vorgehen.
Zur Übung: Definiere tail mit tail [a1,...,an] = [a2,...,an].
Sowohl head als auch tail bleiben auch in dieser Form partielle Funktionen, weil die Funktion
error ja kein Ergebnis liefert, sondern die Rechnung abbricht. Alternativ zur Benutzung von error
können wir beide Funktionen auch zu totalen Funktionen machen: Der Ergebnistyp wird um ein Element
erweitert, das gerade „undefiniert“ repräsentiert. Diesem Zweck dient ja der Typkonstruktor
Maybe.
head’ :: [Integer] -> Maybe Integer
head’ [] = Nothing
head’ (a:x) = Just a
Zur Übung: Definiere ein Pendant zu tail.
Welche der beiden Varianten man verwendet, hängt stark vom Anwendungsfall ab. In der Regel
wird es die erste sein, da diese bequemer ist: Z.B. sind head x:tail x oder tail (tail x)
wohlgetypte Ausdrücke, head’ x:tail’ x oder tail’ (tail’ x) hingegen nicht. Aber man
muß als Programmiererin darauf achten, daß head und tail stets richtig aufgerufen werden. Die
zweiten Varianten ermöglichen, nein sie erzwingen es sogar, daß ein möglicher Fehler behandelt
wird.
Die Disjunktheit der Mustergleichungen ist verletzt, wenn es Argumente gibt, für die mehrere
Gleichungen passen. Ein Beispiel dafür ist die Definition von words:
words :: String -> [String]
words xs = wds [] xs
ws :: String -> String -> [String]
wds "" "" = []
wds ws "" = [reverse ws]
wds "" (’ ’:xs) = wds "" xs
wds "" ( x :xs) = wds [x] xs
wds ws (’ ’:xs) = (reverse ws) : wds "" xs
wds ws ( x :xs) = wds (x:ws) xs
Die dritte Gleichung für wds paßt auch dann, wenn die zweite paßt: Schließlich kann x ja ein
beliebiges Zeichen, also auch ’ ’ sein. Ebenso paßt die fünfte Gleichung auch dann, wenn die
vierte paßt. Klar: um diese Situation zu vermeiden, müßte man statt Gleichung 3 je eine Gleichung
für alle ASCII-Zeichen außer dem Leerzeichen anführen.
Im Falle nicht disjunkter Mustergleichungen gilt die Regel: Es ist stets die erste (im Sinne der
Aufschreibung) passende Gleichung anzuwenden.

3.3. Ausdrücke 43
3.3. Ausdrücke
Wenn wir rechnen, manipulieren wir Ausdrücke. Von daher ist es höchste Zeit, daß wir uns
den Aufbau von Ausdrücken genauer anschauen. Neben der Vertiefung bereits bekannter
Konstrukte werden wir drei neue Arten von Ausdrücken kennenlernen. Diese zählen zu
den grundlegenden Sprachkonstrukten von Haskell – grundlegend in dem Sinn, daß sie
zwar weiter von der gewohnten mathematischen Notation entfernt, dafür aber allgemeiner
sind und sich viele bisher besprochenen Konstrukte als vereinfachte Schreibweise aus
ihnen ableiten lassen. Die grundlegenden Konstrukte werden wir insbesondere verwenden,
um in Abschnitt 3.5 das Rechnen in Haskell formal zu definieren.
3.3.1. Variablen, Funktionsanwendungen und Konstruktoren
Im einfachsten Fall besteht ein Ausdruck aus einem Bezeichner. Damit ein solcher Ausdruck
Sinn macht, muß der Bezeichner irgendwo eingeführt worden sein, entweder in
einer Definition oder als Parameter einer Funktion. Egal hingegen ist, ob der Bezeichner
eine Funktion bezeichnet, eine Liste oder ein Musikstück.
Die Anwendung einer Funktion f auf Argumente e1, . . . , en notieren wir einfach, indem
wir die Funktion und die Argumente hintereinanderschreiben: f e1 . . . en. Sowohl f
als auch die ei können wiederum beliebige Ausdrücke sein, vorausgesetzt die Typen der
Ausdrücke ei passen zu den Typen der Funktionsparameter: Damit f e1 . . . en wohlgetypt
ist, muß f den Typ σ1-> · · · ->σn->τ und ei den Typ σi haben. In diesem Fall besitzt
f e1 . . . en den Typ τ. Sind die Argumente wiederum Funktionsanwendungen, müssen diese
in Klammern gesetzt werden wie z.B. in min a (minimum as). Lassen wir die Klammern
fälschlicherweise weg, versorgen wir min ungewollt mit drei Argumenten, wobei
das zweite Argument eine Funktion ist.
Die Elemente eines Datentyps werden durch Konstruktoren aufgebaut. Die Anwendung
eines Konstruktors auf Argumente wird genauso notiert wie die Anwendung einer Funktion.
Konstruktoren unterscheiden sich von Funktionen nur dadurch, daß sie in Mustern
vorkommen dürfen.
Infix-Notation
Als Infix-Operatoren bezeichnet man (zweistellige) Funktionen, die zwischen ihre Argumente
geschrieben werden. Um Klammern zu sparen, werden Operatoren Prioritäten
oder Bindungsstärken zugeordnet: die Multiplikation (+) bindet z.B. stärker als die Addition
(+); somit entspricht a + b * c dem Ausdruck a + (b * c). Außerdem legt
man fest, ob Operatoren links, rechts oder gar nicht assoziativ sind: Die Subtraktion
Grit Garbo: Das ist doch wahrlich nicht aufregend: Punkt- vor
Strichrechnung kennt man doch schon aus dem Kindergarten.

Lisa Lista: Witzig: Wenn (-) rechts assoziierte, dann wären
a - b - c und a - b + c gleichbedeutend.
Bindungs- links- nicht rechtsstärke
assoziativ assoziativ assoziativ
9 !! .
8 ˆ, ˆˆ, **
7 *, /,
‘div‘, ‘mod‘,
‘rem‘, ‘quot‘
6 +, -
5 \\ :, ++
4 ==, /=, =,
‘elem‘,
‘notElem‘
3 &&
2 ||
1 >>, >>=
0 $, ‘seq‘
Tabelle 3.1: Bindungsstärken der vordefinierten Operatoren
Grit Garbo: Das ist mir völlig unverständlich! Warum sind (+)
und (*) linksassoziativ, (++) aber rechtsassoziativ? Alle diese
Operatoren sind doch assoziativ.
Übung 3.5 Versuche Grit zu helfen.
44 3. Eine einfache Programmiersprache
(-) zum Beispiel assoziiert links, d.h., die Klammern in a - b - c sind so einzufügen:
(a - b) - c. Die Regeln für in Haskell vordefinierte Operatoren findet man in
Tabelle 3.1.
Führen wir selbst neue Infix-Operatoren ein, so müssen ihre Bindungsstärken und assoziativen
Eigenschaften deklariert werden. Wie dies geht, haben wir schon bei (:+:) und
(:*:) (in Kapitel 2) gesehen. Dies muß am Programmanfang geschehen, weil sonst der
Übersetzer solche Formeln gar nicht erst richtig lesen kann.
Die meisten Funktionen scheibt man in Präfix-Schreibweise, also vor ihre Argumente.
Dabei bindet eine Präfix-Funktion immer stärker als Infix-Operatoren. Daher ist f x + 1
gleichbedeutend mit (f x) + 1, und nicht etwa mit f (x + 1). Meint man das Letztere,
muß man eben die Klammern explizit schreiben. Diese Regel erklärt auch die Notwendigkeit
der Klammern in Ausdrücken wie Note ce (1/4). Hat man erst einmal etwas
Haskell-Erfahrung gesammelt, wird man sehen, daß diese Regeln sehr komfortabel sind.
Programmierhinweis: Wir verwenden zwei verschiedene Arten von Bezeichnern: alphanumerische
Bezeichner wie z.B. Note oder transponiere und symbolische wie z.B. „:“ oder „+“. In Haskell
werden symbolische Bezeichner stets infix und alphanumerische stets präfix notiert. Von dieser Festlegung
kann man abweichen, indem man symbolische Bezeichner in runde Klammern einschließt
bzw. alphanumerische in Backquotes: a + b wird so zu (+) a b und div a b zu a ‘div‘ b.
Symbolische Bezeichner können auch für Konstruktoren verwendet werden; einzige Bedingung: der
Name muß mit einem Doppelpunkt beginnen.
3.3.2. Fallunterscheidungen
Elemente eines Datentyps werden mit Hilfe von Konstruktoren konstruiert; sogenannte
case-Ausdrücke erlauben es, Elemente eines Datentyps zu analysieren und entsprechend
ihres Aufbaus zu zerlegen. Konstruktor-basierte Fallunterscheidungen kennen wir schon
von Funktionsbindungen; case-Asudrücke stellen Fallunterscheidungen in Reinform dar
— sie ermöglichen eine Analyse, ohne daß eine Funktionsdefinition vorgenommen werden
muß. Hier ist die Definition von length unter Verwendung eines case-Ausdrucks:
length’ :: [a] -> Int -- vordefiniert
length’ as = case as of
[] -> 0
a:as’ -> 1 + length’ as’
Nach dem Schlüsselwort case wird der Ausdruck aufgeführt, der analysiert werden
soll, der sogenannte Diskriminatorausdruck. Die Behandlung der verschiedenen Fälle oder
Alternativen wird nach dem Schlüsselwort of angegeben, nach dem sich ein lokaler Sichtbarkeitsbereich
für die Alternativen eröffnet. Jede Alternative hat im einfachsten Fall die
Form p -> e, wobei p ein Muster ist und e der Rumpf der Alternative.

3.3. Ausdrücke 45
Ähnlich wie length läßt sich jede Funktionsbindung mit Hilfe von case umschreiben.
Funktionsbindungen können wir somit als eine schönere Notation ansehen für Definitionen,
die als erstes eine case-Unterscheidung auf einem Funktionsargument vornehmen.
Im Vergleich zur Fallunterscheidung mittels Gleichungen sind case-Ausdrücke flexibler
— zum einen da es Ausdrücke sind und zum anderen weil ein Ausdruck und nicht nur ein
Funktionsparameter analysiert werden kann. Betrachte:
last’ :: [a] -> a -- vordefiniert
last’ as = case reverse as of a:as’ -> a
Die Funktion last entnimmt das letzte Element einer Liste, sofern vorhanden, durch
eine Fallunterscheidung auf der umgekehrten Liste.
Von der Form sind case-Ausdrücke Funktionsbindungen jedoch sehr ähnlich. Jede Alternative
kann z.B. Wächter oder lokale Definitionen enthalten:
case e of { p1 m1; . . . ;pn mn }
Die pi sind beliebige Muster und die mi nehmen wahlweise eine der beiden folgenden
Formen an:
oder
-> e where { d1; . . . ;dp }
| g1 -> e1
. . .
| gq -> eq
where { d1; . . . ;dp }
Der where-Teil kann jeweils auch entfallen. Dies entspricht der Form von Funktionsbindungen
mit dem einzigen Unterschied, daß anstelle des Gleichheitszeichens ein Pfeil
steht. Auch für case-Ausdrücke gilt die Abseitsregel, so daß das Ende der Alternativen
bzw. das Ende des gesamten Ausdrucks entweder mittels Layout oder durch Angabe von
Trennsymbolen angezeigt werden kann.
Schauen wir uns noch zwei Beispiele an: Die Funktion words spaltet eine Zeichenkette
in eine Liste von Zeichenketten auf, indem sie an den Leerzeichen trennt.
words :: String -> [String] -- vordefiniert
words cs = case dropSpaces cs of
[] -> []
cs’ -> w : words cs’’
where (w,cs’’) = splitWord cs’

46 3. Eine einfache Programmiersprache
Hier ist eine alternative Definition von minimum0, bei der eine Fallunterscheidung über
das Ergebnis des rekursiven Aufrufs vorgenommen wird.
minimum0’ :: (Ord a) => [a] -> Maybe a
minimum0’ [] = Nothing
minimum0’ (a:as) = case minimum0’ as of
Nothing -> Just a
Just m -> Just (min a m)
3.3.3. Funktionsausdrücke
Betrachten wir einen Ausdruck wie n + 1. In einem Kontext, in dem n gegeben ist,
bezeichnet er einen Wert, den man ausrechnen kann, nachdem man den Wert von n ausgerechnet
hat. Betrachten wir dagegen n als variabel, so stellt der Ausdruck eine Funktion
dar, die in Abhängigkeit von der Variablen n ein Ergebnis berechnet. Genauer gesagt haben
wir: f n = n + 1. Der Name f ist natürlich mehr oder weniger willkürlich gewählt.
Manchmal lohnt es nicht, sich für eine Hilfsfunktion einen Namen auszudenken: Wer viel
programmiert weiß, daß das Erfinden von aussagekräftigen Bezeichnern zu den schwierigsten
Aufgaben gehört. Aus diesem Grund gibt es sogenannte anonyme Funktionen:
Wollen wir ausdrücken, daß n + 1 eine Funktion in Abhängigkeit von n ist schreiben wir
\n -> n + 1
Einen Ausdruck dieser Form nennen wir Funktionsausdruck, da er eine Funktion beschreibt.
Der Schrägstrich (ein abgemagertes λ) läutet den Funktionsausdruck ein, es folgt der formale
Parameter der Funktion und nach dem Pfeil „->“ der Rumpf der Funktion. Wir haben
bereits gesehen, daß in Haskell für Ausdrücke und Typen häufig die gleiche Notation verwendet
wird. Funktionsausdrücke sind dafür ein gutes Beispiel: Wenn x den Typ σ und
e den Typ τ hat, dann besitzt der Ausdruck \x -> e den Typ σ -> τ. Etwas abstrakter
gesehen ist „->“ wie auch Pair ein 2-stelliger Typkonstruktor. Im Unterschied zu Pair
können wir „->“ aber nicht selbst definieren.
Im allgemeinen hat ein Funktionsausdruck die Form
\p1 . . . pn -> e .
Die pi sind beliebige Muster und e ist ein Ausdruck. Hat ein Funktionsausdruck mehr als
einen Parameter, kann er als Abkürzung aufgefaßt werden für entsprechend geschachtelte
Funktionsausdrücke: \p1 p2 -> e ist gleichbedeutend mit \p1 -> \p2 -> e. Für den
zugehörigen Typausdruck gilt dies in ähnlicher Weise: haben wir x1 :: σ1, x2 :: σ2 und
e :: τ, dann ist \x1 -> \x2 -> e vom Typ σ1 -> (σ2 -> τ). Wir vereinbaren, daß
wir rechtsassoziative Klammern weglassen: somit schreiben wir den Typ σ1 -> (σ2 -> τ)
kurz als σ1 -> σ2 -> τ.

3.3. Ausdrücke 47
Die „umgekehrte“ Regel gilt für die Funktionsanwendung: f e1 e2 ist gleichbedeutend
mit (f e1) e2, d.h., die Funktionsanwendung bindet linksassoziativ.
Gestaffelte Funktionen
Wir haben oben so nebenbei angemerkt, daß wir den Ausdruck \p1 p2 -> e als Abkürzung
für \p1 -> \p2 -> e auffassen können. Diesen Sachverhalt wollen wir in diesem
Abschnitt etwas näher beleuchten. Betrachten wir die folgende Definition von add.
add :: Integer -> Integer -> Integer
add m n = m + n
Als Funktionsausdruck geschrieben erhalten wir die folgenden Definition.
add’ :: Integer -> (Integer -> Integer)
add’ = \m -> \n -> m + n
Man ist gewohnt, die Addition zweier Zahlen als zweistellige Funktion zu interpretieren.
Die Definition von add zeigt, daß es auch eine andere — und wie wir gleich sehen
werden pfiffigere — Interpretation gibt: add ist eine einstellige Funktion, die eine einstellige
Funktion als Ergebnis hat. Somit ist add 3 eine einstellige Funktion, die ihr Argument
um 3 erhöht: \n -> 3 + n. Die Argumente werden also peu à peu übergeben. Aus diesem
Grund nennen wir Funktionen des Typs σ1 -> σ1 -> · · · σn -> τ mit n 2 auch
gestaffelt. Sie werden auch „curryfizierte“ oder „geschönfinkelte“ Funktionen genannt,
nach den Logikern Haskell B. Curry und Moses Schönfinkel. Daher erklärt sich der Name
Haskell.
Bevor wir zu den Vorteilen gestaffelter Funktionen kommen, merken wir an, daß add
alternativ auch auf Paaren definiert werden kann.
add0 :: (Integer,Integer) -> Integer
add0 (m,n) = m+n
Die Funktion add0 ist ebenfalls einstellig — auch wenn man in der Mathematik Funktionen
auf Cartesischen Produkten n-stellig nennt. Der einzige Parameter ist eben ein
Paar. Im Unterschied zu „echten“ mehrstelligen Funktionen kann das Argument von add0
ein beliebiger Ausdruck sein, der zu einem Paar auswertet.
dup :: a -> (a, a)
dup a = (a,a)
double :: Integer -> Integer
double n = add0 (dup n)
Grit Garbo: Schließlich bin ich kein Computer und kann den
Typ sehen wie ich will — ob Klammern oder nicht.

Übung 3.6 Wann sind Funktionen auf Cartesischen Produkten
besser geeignet?
48 3. Eine einfache Programmiersprache
Der Vorteil von gestaffelten Funktionen gegenüber ihren Kolleginnen auf Cartesischen
Produkten ist, daß sie Ableger bilden, wenn man ihnen nur einen Teil der Argumente gibt.
Betrachten wir die folgende Definition:
note :: Int -> Int -> Dauer -> Musik
note oct h d = Note (12 * oct + h) d
Füttert man note nach und nach mit Argumenten, so erhält man folgende Ableger:
note Eine Note in einer beliebigen Oktave und von beliebiger Höhe und Dauer.
note 2 Eine Note in der dritten Oktave und von beliebiger Höhe und Dauer.
note 2 ef Die Note f in der dritten Oktave und von beliebiger Dauer.
note 2 ef (1/4) ergibt Note 29 (1/4).
Durch die gestaffelte Form ist eine Funktion also vielseitiger einsetzbar als bei Verwendung
des Cartesischen Produkts als Argumentbereich.
Noch eine terminologische Bemerkung: Man spricht von Funktionen höherer Ordnung,
wenn Argument- oder Ergebnistyp oder beide Funktionstypen sind. Somit sind add und
note Funktionen höherer Ordnung. Im Grunde sind fast alle Programme, die wir bisher
kennengelernt haben, aus Funktionen höherer Ordnung aufgebaut. Auch wenn man nicht
immer daran denkt.
3.3.4. Lokale Definitionen
Lokale Definitionen können nicht nur mit Gleichungen, sondern mit beliebigen Ausdrücken
verknüpfen werden. Letzteres geschieht durch sogenannte let-Ausdrücke. Die
folgende Definition von power benutzt let statt where und if anstelle von Wächtern.
power’ :: (Integral b, Num a) => a -> b -> a
power’ x n = if n == 0 then 1
else let y = power’ (x*x) (n ‘div‘ 2)
in if n ‘mod‘ 2 == 0 then y
else y*x
Nach dem Schlüsselwort let werden die Hilfsdefinitionen angegeben (hier ist es nur
eine), entweder in geschweifte Klammern eingeschlossen und durch jeweils ein Semikolon
getrennt oder unter Benutzung der Abseitsregel. Der Ausdruck, in dem die Namen gültig
sind, folgt nach dem Schlüsselwort in. Den obigen let-Ausdruck liest man „sei y gleich
. . . in . . . “. Im allgemeinen haben let-Ausdrücke die Form
let {e1; . . . ; en} in e .

3.4. Anwendung: Binärbäume 49
Ein let-Ausdruck führt neue Namen ein, genau wie case-Ausdrücke und Funktionsausdrücke.
Schauen wir uns ihre Sichtbarkeitsbereiche genauer an:
case e of { . . . ;pi mi; . . . } Die in pi eingeführten Variablen sind in mi sichtbar.
\p1 . . . pn -> e Die Variablen in p1, . . . , pn sind in e sichtbar.
let {d1; . . . ;dn} in e Die in den di eingeführten Variablen sind in e und in den Definitionen
di selbst sichtbar.
Im Unterschied zur where-Klausel ist der let-Ausdruck ein Ausdruck und kann überall
da stehen, wo Ausdrücke erlaubt sind. Die where-Klausel ist hingegen syntaktischer
Bestandteil einer Gleichung.
Der bis hierher eingeführte Ausschnitt aus der Programmiersprache Haskell reicht für
die nun folgenden Anwendungen aus. Wir haben diesen Ausschnitt so gewählt, daß er
einen einfachen intuitiven Zugang bietet, insbesondere was das Rechnen (lassen) betrifft.
Wer mehr über die Sprache Haskell wissen möchte, insbesondere auch präzisere Definitionen
zur Frage „Wie rechnet Haskell“ sehen möchte, findet dies in dem vertiefenden
Abschnitt 3.5. Andernfalls kann man sich auch nach dem Studium des nächsten Abschnitts
getrost den allgemeineren Themen der nächsten Kapitel zuwenden.
3.4. Anwendung: Binärbäume
In Kapitel 2 haben wir an zwei Beispielen gesehen, wie man Objekte der Realität durch
Formeln nachbildet. Nun entspringen nicht alle Formeln, mit denen sich die Informatik
beschäftigt, einem derartigen Modellierungsprozeß. Viele Formeln, genannt Datenstrukturen,
sind Informatik-intern entwickelt worden, um Probleme mittelbar besser lösen zu
können. Mit einer derartigen Datenstruktur, sogenannten Binärbäumen, beschäftigen wir
uns in diesem Abschnitt. Die einleitenden Worte deuten darauf hin, daß Binärbäume keine
biologischen Bäume modellieren. Die biologische Metapher dient hier lediglich als
Lieferant für Begriffe: So haben Binärbäume eine Wurzel, sie haben Verzweigungen und
Blätter.
Zwei Beispiele für Binärbäume sind in Abbildung 3.1 aufgeführt. Zunächst einmal fällt
auf, daß die Informatik die Bäume auf den Kopf stellt: die Wurzel der Bäume ist oben
und die Blätter sind unten. 2 Binärbäume bestehen aus drei verschiedenen Komponenten:
Es gibt binäre Verzweigungen (dargestellt als Kreise), beschriftete Blätter (dargestellt
als Quadrate) und unbeschriftete Blätter (symbolisiert durch ɛ). 3 Für die Darstellung von
2Diese Darstellung erklärt sich mit der im westlichen Kulturkreis üblichen Lese- und Schreibrichtung von oben
nach unten.
3Es gibt auch Varianten von Binärbäumen, die beschriftete Verzweigungen und unbeschriftete Blätter haben.
1 2
3 1 ɛ
2 3 ɛ 4
Abbildung 3.1: Beispiele für Binärbäume

Übung 3.7 Notiere die folgenden Bäume als Terme:
1 2
ɛ 1 2
3 ɛ 4 5
1 2 3
(1) (2) (3)
4
7 8
5 6
Übung 3.8 Zeichne die zu den folgenden Formeln korrespondierenden
Bäume.
1. Br Nil (Br (Leaf 1) (Leaf 2))
2. Br (Br (Br (Leaf 1) (Leaf 2))
(Br Nil (Leaf 3)))
(Br (Leaf 4) (Leaf 5))
3. Br (Br (Leaf 1) (Leaf 2))
(Br (Br (Br (Br (Leaf 3) (Leaf 4))
(Leaf 5))
(Leaf 6))
(Br (Leaf 7) (Leaf 8)))
Lisa Lista: Harry, probier leaves doch mal aus!
Harry Hacker: Hey, Du hast wohl den Übergang vom Rechnen
zum Rechnen lassen geschafft :-). [Harry wirft seinen Missile
DX mit Turbo-Haskell an und tippt die Definitionen ab.] Was
sollen wir denn rechnen lassen?
Lisa Lista: Wie wär’s mit leaves (leftist [0 .. 9])?
Harry Hacker: [Harry tippt den Ausdruck ein und die Liste
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0] erscheint prompt am
Bildschirm.] Dauert doch gar nicht so lange wie die sagen.
Lisa Lista: [Lisa schiebt Harry beiseite und tippt eifrig
leaves (leftist [0 .. n]) für immer größere n ein. Für
n = 5000 kann man die Ausgabe der Elemente gemütlich am
Bildschirm verfolgen.] Langsam, aber sicher geht Dein Missile
DX in die Knie, Harry.
50 3. Eine einfache Programmiersprache
Binärbäumen mit Formeln, müssen wir uns Namen für die aufgeführten Bestandteile ausdenken:
data Tree a = Nil
| Leaf a
| Br (Tree a) (Tree a)
Der Typ Tree a umfaßt somit binäre Bäume über dem Grundtyp a: Ein Baum ist entweder
leer, oder ein Blatt, das ein Element vom Typ a enthält, oder eine Verzweigung
(engl.: Branch) mit zwei Teilbäumen. Wie der Listentyp ist auch Tree ein Typkonstruktor:
Tree ist mit dem Typ der Blattmarkierungen parametrisiert.
Mit Hilfe der neuen Formeln können wir die Bäume aus Abbildung 3.1 als Terme notieren:
t1, t2 :: Tree Integer
t1 = Br (Br (Leaf 1) (Leaf 2)) (Leaf 3)
t2 = Br (Br (Leaf 1) Nil)
(Br (Br (Leaf 2) (Leaf 3))
(Br Nil (Leaf 4)))
Stellen wir uns die Aufgabe, die Blätter eines Baums in einer Liste aufzusammeln. Für
t1, den linken Baum aus Abbildung 3.1, ergibt sich:
leaves (Br (Br (Leaf 1) (Leaf 2)) (Leaf 3)) ⇒ [1, 2, 3]
Man sieht, daß die Reihenfolge der Elemente in der Liste der Reihenfolge der Blätter
im Baum entspricht (jeweils von links nach rechts gelesen). Hier ist eine einfache — und
wie wir gleich sehen werden naive — Lösung für das Problem:
leaves :: Tree a -> [a]
leaves Nil = []
leaves (Leaf a) = [a]
leaves (Br l r) = leaves l ++ leaves r
Im letzten Fall — die Wurzel ist eine Verzweigung — werden die Blätter des linken und
des rechten Teilbaums mit (++) konkateniert. Die Definition ist elegant, aber in einigen
Fällen auch sehr rechenintensiv. Dies liegt an der Verwendung der Listenkonkatenation:
Sei ni die Länge der Liste xi; um x1 ++ x2 auszurechnen, muß die zweite Gleichung für
(++) genau n1 mal angewendet werden. Ist nun der linke Teilbaum jeweils sehr groß und
der rechte klein oder leer, dann wird wiederholt in jedem Rekursionsschritt eine große
Liste durchlaufen. Die folgende Funktion generiert bösartige Fälle:
leftist :: [a] -> Tree a
leftist [] = Nil
leftist (a:as) = Br (leftist as) (Leaf a)

3.4. Anwendung: Binärbäume 51
Da die Listenkonkatenation die Rechenzeit in die Höhe treibt, stellt sich die Frage, ob
wir bei der Definition von leaves auch ohne auskommen. Identifizieren wir zunächst die
einfachen Fälle: Ist der Baum leer oder ein Blatt, können wir das Ergebnis sofort angeben.
Wenn der Baum eine Verzeigung ist, deren linker Teilbaum leer oder ein Blatt ist, kommen
wir ebenfalls ohne (++) aus.
leaves’ :: Tree a -> [a]
leaves’ Nil = []
leaves’ (Leaf a) = [a]
leaves’ (Br Nil r) = leaves’ r
leaves’ (Br (Leaf a) r) = a : leaves’ r
Es fehlt der Fall, daß der linke Teilbaum selbst wieder eine Verzweigung ist. Jetzt wenden
wir einen Trick an: Wir machen den linken Teilbaum kleiner, indem wir die Bäume
umhängen, und rufen leaves wieder rekursiv auf. Beim Umhängen müssen wir darauf
achten, daß sich die Reihenfolge der Elemente nicht ändert.
leaves’ (Br (Br l’ r’) r) = leaves’ (Br l’ (Br r’ r))
Auf diese Weise nähern wir uns Schritt für Schritt einem der oben aufgeführten, einfachen
Fälle. Das Umhängen der Bäume ist in Abbildung 3.2 grafisch dargestellt. Aus naheliegenden
Gründen wird die Transformation auch als Rechtsrotation bezeichnet. Rechnen
wir leaves’ t1 aus. In den Kommentaren geben die Zahlen die jeweils verwendete
Gleichung an.
leaves’ (Br (Br (Leaf 1) (Leaf 2)) (Leaf 3))
⇒ leaves’ (Br (Leaf 1) (Br (Leaf 2) (Leaf 3))) (Def. leaves’.5)
⇒ 1 : leaves’ (Br (Leaf 2) (Leaf 3)) (Def. leaves’.4)
⇒ 1 : 2 : leaves’ (Leaf 3) (Def. leaves’.4)
⇒ 1 : 2 : [3] (Def. leaves’.2)
Der Nachweiß, daß leaves’ für die Erledigung der gleichen Aufgabe tatsächlich mit
weniger Schritten auskommt, steht natürlich noch aus. Wir führen ihn in Kapitel 5, in
dem wir uns intensiv mit dem Thema Effizienz auseinandersetzen.
Programmieren wir eine Umkehrung von leaves, d.h. eine Funktion build mit
leaves (build x) = x für alle Listen x. Diese Eigenschaft läßt uns Spielraum, denn es
gibt viele Bäume, die von leaves auf die gleiche Liste abgebildet werden: leaves ist
surjektiv. Wir nutzen diese Wahlmöglichkeit und konstruieren einen Baum, bei dem die
Blätter möglichst gleichmäßig auf die Äste verteilt sind. Hat die Liste n Elemente, so verteilen
wir ⌊n/2⌋ Elemente auf den linken und ⌈n/2⌉ Elemente auf den rechten Teilbaum.
Somit unterscheidet sich für jede Verzweigung die Größe der Teilbäume um maximal ein
Element. Bäume mit dieser Eigenschaft nennt man ausgeglichen.
Harry Hacker: Jetzt vergleichen wir mal! [Harry gibt den
Ausdruck leaves’ (leftist [0 .. 5000]) ein. Die Liste
[5000, 4999 .. 0] saust über den Bildschirm.] Ich bin beeindruckt.
Übung 3.9 Programmiere leaves’ mit case-Ausdrücken. Verwende
dabei nur einfache Muster (ein Konstruktor angewendet
auf Variablen ist ein einfaches Muster).
t u
v
=⇒
t
Abbildung 3.2: Rechtsrotation
u
v

Übung 3.10 Definiere die Funktion drop, die eine Liste auf die
Liste ohne ihre ersten k Elemente abbildet.
1 2 3
4 5
6
7 8
9
10 11
Abbildung 3.3: Ausgeglichener Baum der Größe 11
52 3. Eine einfache Programmiersprache
build :: [a] -> Tree a
build [] = Nil
build [a] = Leaf a
build as = Br (build (take k as)) (build (drop k as))
where k = length as ‘div‘ 2
Die Hilfsfunktion take entnimmt die ersten k Elemente einer Liste. Die Funktion drop
wird in Übung 3.10 besprochen.
take :: Int -> [a] -> [a] -- vordefiniert
take (n+1) (a:as) = a : take n as
take _ _ = []
In Abbildung 3.3 ist das Ergebnis von build [1 .. 11] grafisch dargestellt. Die
Struktur ergibt sich aus der wiederholten Halbierung von 11:
11
= 5 + 6
= (2 + 3) + (3 + 3)
= (1 + 1) + (1 + 2) + (1 + 2) + (1 + 2) .
Auch für build geben wir noch eine bessere, weil schnellere Definition an. Eine Inspektion
von build zeigt, daß bei jedem rekursiven Aufruf die Argumentliste dreimal
durchlaufen wird: einmal in gesamter Länge von length und zweimal jeweils bis zur
Hälfte von take und drop. Wir können die wiederholten Durchläufe vermeiden, indem
wir mehrere Schritte zusammenfassen. Zu diesem Zweck definieren wir eine Hilfsfunktion
buildSplit mit der folgenden Eigenschaft: Sei 0 n length x, dann gilt
buildSplit n x = (build (take n x), drop n x)
Die Funktion build erhalten wir, indem wir buildSplit mit der Listenlänge aufrufen.
build’ :: [a] -> Tree a
build’ as = fst (buildSplit (length as) as)
Die Funktion buildSplit ergibt sich zu:
buildSplit :: Int -> [a] -> (Tree a, [a])
buildSplit 0 as = (Nil, as)
buildSplit 1 as = (Leaf (head as), tail as)
buildSplit n as = (Br l r, as’’)
where k = n ‘div‘ 2
(l,as’) = buildSplit k as
(r,as’’) = buildSplit (n-k) as’

3.5. Vertiefung: Rechnen in Haskell 53
Man kann die Definition von buildSplit sogar systematisch aus der obigen Eigenschaft
herleiten. Dazu mehr in Kapitel 4. Den Nachweis, daß build’ besser ist als build,
holen wir in Kapitel 5 nach.
3.5. Vertiefung: Rechnen in Haskell
3.5.1. Eine Kernsprache/Syntaktischer Zucker
Reduktion auf Kernsprache: Mustergleichungen lassen sich auf einfachere Gleichungen zurückführen,
die keine Fallunterscheidung auf der linken Seite treffen, sondern stattdessen
rechts case-Ausdrücke verwenden.
Wo wir gerade bei Abkürzungen sind: Funktionsdefinitionen können wir ebenfalls als
eine abkürzende Schreibweise auffassen: f x = e kürzt f = \x -> e ab. Dito für mehrstellige
Funktionsdefinitionen: g x1 x2 = e kürzt g = \x1 x2 -> e ab. where-
Klauseln wiederum können wir durch let-Ausdrücke ersetzen.
Eine Rechnung wird durch die Angabe eines Ausdrucks gestartet, der relativ zu den im
Programm aufgeführten Definitionen ausgerechnet wird. Im Prinzip kann man ein Programm
als großen let-Ausdruck auffassen: Nach dem let stehen alle Definitionern des
Programms, nach dem in der zu berechnende Ausdruck. Vordefinierte Typen und Funktionen
haben globale Sichtbarkeit.
Hat man sich einmal auf diese Kernsprache beschränkt, kann man das Rechnen in Haskell
durch drei Rechenregeln — für Funktionsanwendungen, case- und let-Ausdrücke
— erklären.
3.5.2. Auswertung von Fallunterscheidungen
Voraussetzung: nur einfache case-Ausdrücke.
Ein case-Ausdruck kann ausgerechnet werden, wenn der Diskriminatorausdruck ein
Konstruktorausdruck ist: case C e1 ... ek of .... In diesem Fall wissen wir, welche
der nach of angegeben Alternativen vorliegt. Nehmen wir an, C x1 ... xk -> e ist
die passende Alternative, dann läßt sich der case-Ausdruck zu e vereinfachen, wobei wir
die Argumente des Konstruktors e1, . . . , ek für die Variablen x1, . . . , xk einsetzen müssen.
Das Muster fungiert also als eine Art Schablone.
abs :: (Ord a, Num a) => a -> a -- vordefiniert
abs n = case n >= 0 of
True -> n
False -> -n
encode :: (Num a) => Maybe a -> a
Harry Hacker: Hmm — die Laufzeiten von build und build’
unterscheiden sich nicht so dramatisch.

Übung 3.11 Stelle abgeleitete Regeln für if auf.
54 3. Eine einfache Programmiersprache
encode x = case x of
Nothing -> -1
Just n -> abs n
encode (Just 5)
⇒ case Just 5 of {Nothing -> -1; Just n -> abs n} (Def. encode)
⇒ abs 5 (case − Regel)
⇒ case 5 >= 0 of {True -> 5; False -> -5} (Def. abs)
⇒ case True of {True -> 5; False -> -5} (Def. >=)
⇒ 5 (case − Regel)
Für die gleichzeitige Ersetzung von Variablen durch Ausdrücke verwenden wir die Notation
e[x1/e1, . . . , xn/en]. Damit bezeichnen wir den Ausdruck, den man aus e erhält, wenn
man alle Vorkommen von xi gleichzeitig durch ei ersetzt. Damit läßt sich unsere erste
Rechenregel formalisieren.
case C e1...ek of {...; C x1...xk -> e;...} (case-Regel)
⇒ e[x1/e1, . . . , xn/en]
Mit den Auslassungspunkten „. . . “ sollen jeweils die nicht passenden Alternativen symbolisiert
werden.
3.5.3. Auswertung von Funktionsanwendungen
Wir erklären nun formal, wie man mit Funktionsausdrücken rechnet.
Eine Funktionsanwendung f a kann erfolgen, wenn f ein Funktionsausdruck ist: (\x ->
e) a. Dann läßt sich die Anwendung zu e vereinfachen, wobei wir den aktuellen Parameter
a für den formalen Parameter x einsetzen. Etwas ähnliches haben wir schon beim
Ausrechnen von case-Ausdrücken kennengelernt. Die neue Rechenregel läßt sich einfach
formalisieren:
\(x -> e) a ⇒ e[x/a] (β-Regel) (3.2)
Der Name β-Regel ist genau wie der Schrägstrich bei Funktionsausdrücken, der ein λ
symbolisiert, historisch begründet. Aus nostalgischen Gründen übernehmen wir beides.

3.5. Vertiefung: Rechnen in Haskell 55
Wiederholen wir noch einmal die Auswertung von encode (Just 5) aus Abschnitt 3.5.2.
Wir werden sehen, daß wir die β-Regel schon heimlich verwendet haben, ohne uns große
Gedanken darüber zu machen. Zunächst schreiben wir encode und abs als Funktionsausdrücke
auf:
abs = \n -> case n >= 0 of {True -> n; False -> -n}
encode = \x -> case x of {Nothing -> -1; Just n -> abs n}
Die Rechnung nimmt jetzt den folgenden Verlauf.
encode (Just 5) (Def. encode)
⇒ (\x-> case x of {Nothing-> -1; Just n-> abs n}) (Just 5)
⇒ case Just 5 of {Nothing -> -1; Just n -> abs n} (β − Regel)
⇒ abs 5 (case − Regel)
⇒ (\n -> case n >= 0 of {True -> n; False -> -n}) 5 (Def. abs)
⇒ case 5 >= 0 of {True -> 5; False -> -5} (β − Regel)
⇒ case True of {True -> 5; False -> -5} (Def. (>=))
⇒ 5 (case − Regel)
In der ersten Rechnung haben wir zwei Schritte zusammengefaßt: Das Einsetzen der
Definition von encode bzw. von abs und die Anwendung der β-Regel. Schauen wir uns
noch ein weiteres Beispiel an. [Das Beispiel gehört in die Schublade der akademischen
Beispiele; es erlaubt aber, die Anwendung der β-Regel innerhalb von 9 Schritten immerhin
6-mal einzuüben.]
twice :: (a -> a) -> a -> a
twice = \f -> \a -> f (f a)
Wir rechnen den Ausdruck twice twice inc aus. Ist klar, was als Ergebnis herauskommt?
twice twice inc
⇒ (\f -> \a -> f (f a)) twice inc (Def. twice)
⇒ (\a -> twice (twice a) inc (β − Regel)
⇒ twice (twice inc) (β − Regel)
⇒ twice ((\f -> \a -> f (f a)) inc) (Def. twice)
⇒ twice (\a -> inc (inc a)) (β − Regel)
⇒ (\f -> \a -> f (f a)) (\a -> inc (inc a)) (Def. twice)
⇒ \a -> (\a -> inc (inc a)) ((\a -> inc (inc a)) a) (β − Regel)
⇒ \a -> (\a -> inc (inc a)) (inc (inc a)) (β − Regel)
⇒ \a -> inc (inc (inc (inc a))) (β − Regel)

56 3. Eine einfache Programmiersprache
Man sieht, wir können rechnen, ohne uns Gedanken über die Bedeutung machen zu
müssen. Und das ist auch gut so, schließlich wollen wir ja rechnen lassen.
Trotzdem ist es interessant zu fragen, was twice twice eigentlich bedeutet. Nun, der Ausdruck
twice inc bezeichnet laut Definition die 2-fache Anwendung von inc auf ein Argument;
die Rechnung zeigt, daß twice twice inc der 4-fachen Anwendung von inc entspricht. Und
twice twice twice inc oder gar twice twice twice twice inc?
Versuchen wir die Ausdrücke intelligent auszurechnen, indem wir Gesetzmäßigkeiten aufdecken.
Jetzt müssen wir erfinderisch sein und mit den Formeln spielen. Die Arbeit nimmt uns kein Rechner
ab, Gott sei Dank, oder? Als erstes erfinden wir eine Notation für die n-fache Anwendung: 〈n〉.
Also, twice = 〈2〉 und twice twice = 〈4〉. Definieren können wir 〈n〉 mithilfe der Komposition:
〈n〉 f = f ◦ · · · ◦ f.
Wenden wir nun 〈m〉 auf 〈n〉 an, komponieren wir 〈n〉 m-mal mit sich selbst. Das
| {z }
n-mal
führt uns zu der Frage, was 〈m〉 ◦ 〈n〉 bedeutet? Nun, 〈n〉 f ist f ◦ · · · ◦ f , mit 〈m〉(〈n〉 f) wiederholt
| {z }
n-mal
sich dieser Ausdruck m-mal: (f ◦ · · · ◦ f) ◦ · · · ◦ (f ◦ · · · ◦ f) . Ergo, erhalten wir 〈mn〉. Nun können
| {z }
m-mal
wir auch 〈m〉 〈n〉 erklären: 〈m〉 〈n〉 = 〈n〉 ◦ · · · ◦ 〈n〉 = 〈n
| {z }
m-mal
m 〉. Somit ist (〈2〉 〈2〉) 〈2〉 = 〈4〉 〈2〉 = 〈16〉
und ((〈2〉 〈2〉) 〈2〉) 〈2〉 = 〈16〉 〈2〉 = 〈65536〉. Geschafft!
3.5.4. Auswertung von lokalen Definitionen
Voraussetzung: nur einfache let-Ausdrücke.
Die let-Ausdrücke haben uns noch gefehlt: Mit ihnen ist unsere Programmiersprache
komplett. Im folgenden erklären wir, wie man mit ihnen rechnet.
Wenn die Definitionen nicht rekursiv sind, ist die Rechenregel einfach: Die definierenden
Ausdrücke werden für die Bezeichner in den Rumpf des let-Ausdrucks eingesetzt.
let {x1 = e1;...;xn = en} in e
⇒ e[x1/e1, . . . , xn/en]
Wenn die Definitionen rekursiv sind, geht das nicht so einfach. Die Bezüge für die in den
rechten Seiten auftretenden Bezeichner gïngen sonst verloren. Eine rekursive Definition
wird unter Umständen wiederholt benötigt, etwa für jede rekursive Anwendung einer
Funktion. Um für diesen Fall gerüstet zu sein, ersetzen wir xi statt durch ei durch den
Ausdruck let {x1 = e1;...;xn = en} in ei.

3.5. Vertiefung: Rechnen in Haskell 57
let {x1 = e1;...;xn = en} in e
⇒ e[x1/let {x1 = e1;...;xn = en} in e1, . . . , (let-Regel)
xn/let {x1 = e1;...;xn = en} in en]
Die lokalen Definitionen werden auf diese Weise einmal aufgefaltet. Das bläht den Ausdruck
zunächst einmal gewaltig auf — aber danach können wir ein Stück weiterrechnen
und ihn (vielleicht) wieder vereinfachen. Beachte, daß die Regel auch funktioniert, wenn
die Definitionen nicht rekursiv sind. Schauen wir uns ein Beispiel an.
rep 2 8
⇒ let x = 8:x in take 2 x (Def. rep)
⇒ take 2 (let x = 8:x in 8:x) (let − Regel)
⇒ take 2 (8:let x = 8:x in 8:x) (let − Regel)
⇒ 8:take 1 (let x = 8:x in 8:x) (Def. take)
⇒ 8:take 1 (8:let x = 8:x in 8:x) (let − Regel)
⇒ 8:8:take 0 (let x = 8:x in 8:x) (Def. take)
⇒ 8:8:[] (Def. take)
Man sieht, die merkwürdige Definition von rep funktioniert. Wir haben uns auch geschickt
angestellt. Für’s erste verlassen wir uns darauf, daß sich auch der Rechner geschickt
anstellt. Später werden wir uns überlegen, warum wir uns darauf verlassen können.
In der obigen Rechnung haben wir einige Schritte zusammengefaßt: Die Anwendung
von take auf die beiden Argumente und die folgenden Fallunterscheidungen erscheinen
als einziger Rechenschritt. Sobald man sich mit der Funktionsweise einer Funktion vertraut
gemacht hat, ist es natürlich und bequem dies zu tun: Wir fassen die Definition von take
sozusagen als abgeleitete Rechenregel auf.
Fazit: Unsere Programmiersprache umfaßt nur sechs grundlegende Arten von Ausdrücken:
Variablen, Konstruktorausdrücke, case-Ausdrücke, Funktionsausdrücke, Funktionsanwendungen
und let-Ausdrücke. Durch die case-, let- und die β-Regel ist das Rechnen in
Haskell formal definiert. Damit können wir alles programmieren, aber nicht unbedingt
lesbar, schön und elegant.
Harry Hacker: Wetten, daß ich diese Rechnung auch mit der
einfachen let-Regel hinkriege?
Lisa Lista: Wetten, daß nicht?
Übung 3.12 Was wäre ungeschickt gewesen?

58 3. Eine einfache Programmiersprache

4. Programmiermethodik
Ziele des Kapitels: In Kapitel 3 haben wir das Werkzeug kennengelernt, das es uns ermöglicht,
rechnen zu lassen. In diesem Kapitel gehen wir einen Schritt weiter und beschäftigen
uns mit dem systematischen Gebrauch dieses Werkzeugs. Dabei gehen wir
vereinfachend davon aus, daß der Prozeß der Modellierung — den wir in Kapitel 2 an
zwei Beispielen kennengelernt haben — bereits abgeschlossen ist. Innerhalb einer vorgegebenen
Modellwelt werden wir uns damit auseinandersetzen, wie man zu ebenfalls
vorgebenen Problemen systematisch Rechenregeln — sprich Programme — entwirft. Als
durchgehendes Beispiel dient uns dabei neben anderen das Sortierproblem.
Eine Bemerkung zur Terminologie sei noch vorausgeschickt: In der Literatur wird oft
eine feinsinnige Unterscheidung zwischen den Begriffen Algorithmus und Programm getroffen.
Ein Algorithmus ist ein Rechenverfahren, daß so präzise beschrieben ist, daß eine
automatische Durchführung im Prinzip möglich ist. Dies gegeben, darf der Algorithmus
auf beliebig hohem Abstraktionsgrad und in beliebiger, hoffentlich dem Problem adäquater
Notation beschrieben sein. Ein Programm ist die Formulierung des Algorithmus in einer
Programmiersprache, so daß man es (bzw. ihn) auch tatsächlich rechnen lassen kann. Früher,
als Programmiersprachen noch wesentlich primitiver waren als heute, spielte dieser
Unterschied eine wesentliche Rolle, und der Übergang vom Algorithmus zum Programm,
manchmal Codierung genannt, war eine nicht zu unterschätzende Fehlerquelle. Dank moderner
Programmiersprachen wie unserem Haskell wird die semantische Lücke zwischen
Algorithmus und Programm ein gutes Stück weit geschlossen, und wir werden die Begriffe
Algorithmus und (Haskell-)Programm praktisch synonym verwenden. Unsere Einführung
in die Informatik kommt dadurch wesentlich zügiger voran, als dies früher möglich war.
4.1. Spezifikation
Bevor man sich daran setzt, Rechenregeln aufzuschreiben, muß man zunächst das Problem
durchdringen, das es zu lösen gilt. Je genauer man das Problem beschreiben kann,
desto besser wird später auch der Entwurf von Rechenregeln gelingen. Das hört sich einleuchtend
an, aber wir werden schnell sehen, daß die Beschreibung eines Problems — in
Fachjargon die Problemspezifikation — alles andere als einfach ist. Wir gehen im folgenden
davon aus, daß das Problem in der Berechnung einer Funktion im mathematischen
Prof. Paneau: Die Autoren vergessen darauf hinzuweisen —
und das sollte man mit der gebotenen Eindringlichkeit tun —
daß nur beständiges Üben zum Erfolg führt.

Harry Hacker: Aber alle meine Programme sind interaktiv; kann
ich jetzt weiterblättern (goto Kapitel 5)?
60 4. Programmiermethodik
Sinne besteht: Einer Eingabe wird eindeutig eine Ausgabe zugeordnet. Wir kümmern uns
damit bewußt nicht um Systeme, die mit einer Benutzerin oder allgemein mit einer Um-
gebung interagieren.
Wie gesagt, wir verwenden das Sortieren als durchgehendes Beispiel. Die informelle
Beschreibung des Sortierproblems ist relativ einfach: Gesucht ist eine Funktion sort, die
eine gegebene Liste von Elementen aufsteigend anordnet. Schauen wir uns ein paar Beispiele
an:
sort [8, 3, 5, 3, 6, 1] ⇒ [1, 3, 3, 5, 6, 8]
sort "hello world" ⇒ " dehllloorw"
sort ["Bein", "Anfall", "Anna"] ⇒ ["Anfall", "Anna", "Bein"]
sort [(1, 7), (1, 3), (2, 2)] ⇒ [(1, 3), (1, 7), (2, 2)]
Kümmern wir uns zunächst um den Typ der Funktion. Die Festlegung des Typs sollte
stets der erste Schritt bei der Spezifikation sein: durch den Typ wird ja gerade die Art der
Eingabe und der Ausgabe beschrieben. Im obigen Beispiel sind Argument und Ergebnis
jeweils Listen; auf den Typ der Listenelemente wollen wir uns nicht festlegen, wir müssen
lediglich annehmen, daß auf den Elementen eine Vergleichsfunktion definiert ist. Somit
erhalten wir:
sort :: (Ord a) => [a] -> OrdList a
Wie läßt sich nun das Sortierproblem formal spezifizieren? Klar, die Ergebnisliste muß
geordnet sein. Diese Eigenschaft kann man mit einer Haskell-Funktion beschreiben.
ordered :: (Ord a) => [a] -> Bool
ordered [] = True
ordered [a] = True
Harry Hacker: Geht das nicht einfacher? Wie wär’s mit „für alle
ordered (a1:a2:as) = a1 [a] muß gelten . . . “. Wir wagen einen ersten Spezifikationsversuch: Sei τ ein beliebiger Typ, auf dem eine
Ordnung definiert ist, für alle Listen x :: [τ] muß gelten
ordered (sort x) = True . (4.1)
Reicht das? Leider nein: die Funktion \x -> [] erfüllt (4.1), aber nicht unsere Erwartungen.
Wir müssen noch fordern, daß alle Elemente der Argumentliste auch in der Ergebnisliste
auftreten. Als zweiten Versuch könnten wir zusätzlich die Listen x und sort x in
Mengen überführen und verlangen, daß beide Mengen gleich sind. Damit haben wir von
der Anordnung der Elemente abstrahiert — aber leider auch von ihrer Anzahl. Schließlich
müssen wir garantieren, daß ein mehrfach auftretendes Element auch noch nach dem Sortieren
in gleicher Anzahl auftritt (siehe erstes Beispiel). Dies kann man mit Mengen nicht
modellieren. Wir spezifizieren diese Eigenschaft, indem wir beide Listen auf eine Struktur

4.1. Spezifikation 61
abbilden, in der die Reihenfolge keine Rolle spielt, aber Elemente mehrfach vorkommen
können: die Struktur der Multimenge.
Die Eigenschaft der geordneten Liste haben wir mit einem Haskell-Programm spezifiziert.
Dies hat den Vorteil, daß wir mit der Spezifikation auch rechnen können, z.B. können
wir sie verwenden, um Sortierprogramme auszutesten. Die Angabe eines Haskell-
Programms für die zweite Eigenschaft ist prinzipiell auch möglich, würde uns aber vom
eigentlichen Thema ablenken. Aus diesem Grund nehmen wir an, daß der Typ Bag a,
Multimengen über dem Grundtyp a, mit folgenden Operationen vorgegeben ist:
∅ die leere Multimenge,
a die einelementige Multimenge, die genau ein Vorkommen von a enthält,
x ⊎ y die Vereinigung der Elemente von x und y; das „+“ im Vereinigungszeichen deutet
an, daß sich die Vorkommen in x und y akkumulieren.
Die Hinzunahme neuer Typen und Operationen mit bestimmten Eigenschaften hat den
Vorteil, daß die Spezifikation einfacher und lesbarer wird. Schließlich ist die Spezifikation
kein Selbstzweck; wir werden sie später verwenden, um die Korrektheit unserer Sortierprogramme
zu beweisen. Für diese Beweise benutzen wir die folgenden Eigenschaften
der Operationen: ∅ ist ein neutrales Element von (⊎) und (⊎) selbst ist assoziativ und
kommutativ.
∅ ⊎ x = x (4.2)
x ⊎ ∅ = x (4.3)
x ⊎ y = y ⊎ x (4.4)
(x ⊎ y) ⊎ z = x ⊎ (y ⊎ z) (4.5)
Die Funktion bag, die eine Liste in eine Multimenge überführt, illustriert die Verwendung
der Operationen.
bag :: [a] -> Bag a
bag [] = ∅
bag (a:as) = a ⊎ bag as
Eine Liste x enthält alle Elemente von y, falls bag x = bag y. In diesem Fall heißt x
Permutation von y. Somit können wir nun spezifizieren: Sei τ ein beliebiger Typ, auf dem
eine Ordnung definiert ist. Für alle Listen x :: [τ] muß gelten
ordered (sort x) = True ∧ bag (sort x) = bag x . (4.6)
Dadurch ist sort als mathematische Funktion, nicht aber als Programm, eindeutig bestimmt.
Harry Hacker: Was unterscheidet jetzt Multimengen von Mengen;
diese Gesetze gelten doch auch für Mengen.
Lisa Lista: Das stimmt Harry. Aber Mengen erfüllen noch eine
weitere Eigenschaft, x ∪ x = x, die auf Multimengen nicht zutrifft.
Übung 4.1
(a) Spezifiziere die Funktion
merge :: (Ord a) =>
OrdList a -> OrdList a -> OrdList a
die zwei geordnete Listen in eine geordnete Liste überführt.
(b) Spezifiziere die Funktion
mergeMany :: (Ord a) =>
[OrdList a] -> OrdList a
die eine Liste geordneter Listen in eine geordnete Liste überführt.

Übung 4.2 Zu implementieren ist eine Funktion
split :: Int -> [a] -> [[a]]
die eine Liste in n möglichst gleich lange Listen aufteilt. Lisa
Lista hat diese Funktion folgendermaßen spezifiziert. Für alle
natürlichen Zahlen n und alle Listen x muß gelten:
concat (split n x) = x ∧ length (split n x) = n .
Harry Hacker hat sofort eine Funktion gefunden, die diese Spezifikation
erfüllt: die Liste x wird in n − 1 leere Listen und die
Liste x selbst „aufgeteilt“. Helfen Sie Lisa bei einer besseren Spezifikation
und bei der Implementierung.
Harry Hacker: [Seufzt] Das kenne ich, meinen Missile DX mußte
ich zum Händler zurückschleppen, weil die Fließkommaarithmetik
des Prozessors fehlerhaft war.
62 4. Programmiermethodik
Manchmal kann man sehr einfach zu einer brauchbaren Spezifikation gelangen, indem
man bereits existierende Funktionen benutzt. Dies haben wir zum Beispiel im Falle von
build getan: Wir haben gefordert, daß build eine Inverse zu leaves sein soll mit der
Eigenschaft leaves (build x) = x für alle x. Damit ist build durchaus nicht eindeu-
tig spezifiziert: Auch
Einstweiliges Fazit: Schon die Spezifikation einfacher Probleme ist nicht unbedingt einfach.
Da wundert es nicht, daß oftmals die Mühe gescheut wird, ein Problem formal
zu spezifizieren. Dabei sind formale Spezifikationen unerläßlich, wenn wir eine Chance
haben wollen, die Korrektheit unserer Programme nachzuweisen. Aber bleiben wir realistisch:
Nach dem heutigen Stand der Forschung wäre es vermessen zu erwarten, daß ein
großes Programmpaket jemals vollständig spezifiziert und als korrekt nachgewiesen wird.
Selbst wenn dies gelänge, hieße das noch nicht, daß „alles läuft“: die Spezifikation kann
falsch sein, oder der Übersetzer oder der Rechner selbst, oder jemand kann den Stecker
herausziehen. Der Schluß, daß es sich damit bei der Programmverifikation um ein nutzlo-
ses Unterfangen handelt, ist aber genauso falsch. Denn mit jedem Korrektheitsnachweis
— auch wenn nur ein kleiner Teil eines umfangreichen Programms berücksichtigt wird —
steigt die Zuverlässigkeit und damit unser Vertrauen in die Software. Kurz gesagt: Lieber
etwas Korrektheit als gar keine.
4.2. Strukturelle Rekursion
Zur Lösung eines Problems braucht man in der Regel eine Idee. Das ist beim Programmieren
nicht anders. Gott sei Dank steht man nicht alleine da. Es gibt einen kleinen Fundus
von Methoden, die sich beim Lösen von Problemen bewährt haben. Eine einfache werden
wir im folgenden kennenlernen, eine weitere in Abschnitt 4.5.
4.2.1. Strukturelle Rekursion auf Listen
Bevor wir uns dem Sortierproblem zuwenden, schauen wir uns zunächst einmal zwei listenverarbeitende
Funktionen aus vorangegangenen Kapiteln an.
translate :: [Codon] -> Protein
translate [] = []
translate (triplet:triplets)
| aminoAcid == Stp = []
| otherwise = aminoAcid:translate triplets
where aminoAcid = genCode triplet
length :: [a] -> Int -- vordefiniert
length [] = 0

4.2. Strukturelle Rekursion 63
length (a:as) = 1 + length as
Beide Funktionen lösen unterschiedliche Probleme; nichtsdestotrotz folgen ihre Definitionen
dem gleichen Schema, das sich eng an der Definition des Listentyps orientiert. Für
jeden in der Datentypdefinition aufgeführten Konstruktor, [] und (:), gibt es eine Gleichung;
der Konstruktor (:) ist rekursiv im zweiten Argument, just über dieses Argument
erfolgt jeweils der rekursive Aufruf. Man sagt, die Funktionen sind strukturell rekursiv
definiert.
Für jeden Datentyp gibt es ein zugehöriges Rekursionsschema, das es erlaubt, Probleme
zu lösen, die Eingaben dieses Datentyps involvieren. Für Listen nimmt das Rekursionsschema
die folgende Form an:
Rekursionsbasis ([]) Das Problem wird für die leere Liste [] gelöst.
Rekursionsschritt (a:as) Um das Problem für die Liste a:as zu lösen, wird nach dem
gleichen Verfahren, d.h. rekursiv, zunächst eine Lösung für as bestimmt, die anschließend
zu einer Lösung für a:as erweitert wird.
Das ganze etwas formaler: Wir sagen, die listenverarbeitende Funktion f ist strukturell
rekursiv definiert, wenn die Definition von der Form
f :: [σ] -> τ
f [] = e1
f (a : as) = e2
where s = f as
ist, wobei e1 und e2 Ausdrücke vom Typ τ sind und e2 die Variablen a, as und s (nicht
aber f) enthalten darf. Mit s wird gerade die Lösung für as bezeichnet; tritt s nur einmal
in e2 auf, kann man natürlich für s auch direkt f as einsetzen.
Wenden wir uns der Lösung des Sortierproblems zu. Es ist eine gute Idee, die Funktionsdefinition
zunächst so weit aufzuschreiben, wie das Rekursionsschema es vorgibt. Wir
erhalten:
insertionSort :: (Ord a) => a -> OrdList a -> OrdList a
insertionSort [] = e1
insertionSort (a : as) = e2
where s = insertionSort as
Wir werden verschiedene Sortieralgorithmen kennenlernen; die Funktionen erhalten jeweils
die in der Literatur gebräuchlichen Namen. Die Lücke in der ersten Gleichung, der
Rekursionsbasis, ist schnell ausgefüllt: die leere Liste ist bereits sortiert, also ersetzen wir
e1 durch []. Zum Rekursionsschritt: Wir müssen die bereits sortierte Liste s um das Element
a erweitern, genauer: a muß in s gemäß der vorgegebenen Ordnung eingefügt werden.
Das hört sich nach einem neuen (Teil-) Problem an. Wie gehen wir weiter vor? Ganz
Prof. Paneau: Das Schema ist doch primitiv, primitiv rekursiv
meine ich.

Prof. Paneau: Ich würde den Autoren empfehlen, ihre Worte
vorsichtiger zu wählen. Die Erweiterung ist doch keine: jede
nach dem g-Schema definierbare Funktion läßt sich bereits mit
dem f-Schema definieren.
Harry Hacker: Wie soll das funktionieren? Die Funktion f hat
einen Parameter, die Funktion g aber zwei!
Prof. Paneau: Lieber Herr Hacker, das ist doch eine Illusion: die
Ausdrücke e1 und e2 können doch funktionswertig sein. Lassen
Sie mich dies am Beispiel der Funktion insert verdeutlichen;
mit dem f-Schema erhalten wir (oBdA habe ich die Parameter
vertauscht):
ins [] = \a -> [a]
ins (a’:as) = \a -> if a [a] -> OrdList a
insertionSort [] = []
insertionSort (a:as) = insert a (insertionSort as)
Wenden wir uns dem neuen Problem zu. Bei der Definition von insert verwenden wir
das Kochrezept ein zweites Mal an. Aber halt, insert hat zwei Parameter; das Rekursionsschema
sieht nur einen Parameter vor. Wir müssen das Schema zunächst erweitern:
Wir sagen, die listenverarbeitende Funktion g ist strukturell rekursiv definiert, wenn die
Definition von der Form
g :: σ1 -> [σ2] -> τ
g i [] = e1
g i (a : as) = e2
where s = g e3 as
ist, wobei e1 die Variable i, e2 die Variablen i, a, as und s und schließlich e3 die Variablen
i, a und as enthalten darf. Häufig, aber nicht immer, ist e3 gleich i, so daß man sich auf
die Wahl von e1 und e2 konzentrieren kann.
Wie oben schreiben wir die Funktionsdefinition für insert zunächst so weit auf, wie
das Rekursionsschema es vorgibt.
insert :: (Ord a) => a -> OrdList a -> OrdList a
insert a [] = e1
insert a (a’ : as) = e2
where s = insert e3 as
Die Rekursionsbasis ist wieder einfach: e1 ist die einlementige Liste [a]. Zum Rekursionsschritt:
Die Argumentliste ist sortiert, damit ist a’ ihr kleinstes Element. Um das erste
Element der Ergebnisliste zu ermitteln, müssen wir a mit a’ vergleichen. Wir erhalten:
insert a [] = []
insert a (a’ : as)
| a a -> [a] -> [a]
insert a [] = [a]

4.2. Strukturelle Rekursion 65
insert a (a’:as)
| a

Übung 4.3 Definiere analog zu size die Funktion
branches :: Tree a -> Integer, die die Anzahl der Verzweigungen
in einem Baum bestimmt.
Übung 4.4 In Abschnitt 3.4 haben wir zwei Definitionen für
leaves angegeben, welche ist strukturell rekursiv?
66 4. Programmiermethodik
4.2.2. Strukturelle Rekursion auf Bäumen
Wir haben bereits angemerkt, daß es für jeden Datentyp ein zugehöriges Rekursionsschema
gibt. Schauen wir uns als weiteres Beispiel das Schema für den Datentyp Tree an, den
wir in Abschnitt 3.4 eingeführt haben.
Rekursionsbasis (Nil) Das Problem wird für den leeren Baum gelöst.
Rekursionsbasis (Leaf a) Das Problem wird für das Blatt Leaf a gelöst.
Rekursionsschritt (Br l r) Um das Problem für den Baum Br l r zu lösen, werden
rekursiv Lösungen für l und r bestimmt, die zu einer Lösung für Br l r erweitert
werden.
Im Unterschied zu Listen gibt es zwei Basisfälle und beim Rekursionsschritt müssen zwei
Teillösungen zu einer Gesamtlösung kombiniert werden. Formal heißt eine Funktion f
strukturell rekursiv, wenn die Definition von der Form
f :: Tree σ -> τ
f Nil = e1
f (Leaf a) = e2
f (Br l r) = e3
where sl = f l
sr = f r
ist. Programmieren wir als Anwendung zwei Funktionen, die Größe bzw. die Tiefe 1 von
Bäumen bestimmen. Die Größe eines Baums setzen wir gleich mit der Anzahl seiner Blätter;
die Tiefe entspricht der Länge des längsten Pfads von der Wurzel bis zu einem Blatt.
size :: Tree a -> Integer
size Nil = 1
size (Leaf _) = 1
size (Br l r) = size l + size r
depth :: Tree a -> Integer
depth Nil = 0
depth (Leaf _) = 0
depth (Br l r) = max (depth l) (depth r) + 1
Auf diese Funktionen werden wir in den nächsten Abschnitten wiederholt zurückkommen,
so daß es sich lohnt, sich ihre Definition einzuprägen.
1 Da die Bäume in der Informatik von oben nach unten wachsen, spricht man eher von der Tiefe eines Baums
und seltener von seiner Höhe.

4.2. Strukturelle Rekursion 67
4.2.3. Das allgemeine Rekursionsschema
Nachdem wir zwei Instanzen des Rekursionsschemas kennengelernt haben, sind wir (hoffentlich)
fit für das allgemeine Kochrezept. Ausgangspunkt ist dabei die allgemeine Form
der Datentypdeklaration, wie wir sie in Abschnitt 3.1.1 kennengelernt haben.
data T a1 . . . am = C1 t11 . . . t1n1
| . . .
| Cr tr1 . . . trnr
Für die Definition des Schemas müssen wir bei den Konstruktoren Ci zwei Arten von
Argumenten unterscheiden: rekursive (d.h. tij ist gleich T a1 . . . am) und nicht-rekursive.
Seien also li1, . . . , lipi mit 1 li1 < li2 < · · · < lipi ni die Positionen, an denen der
Konstruktor Ci rekursiv ist. Das Rekursionsschema besteht nun aus r Gleichungen; für
jeden Konstruktor gibt es eine Gleichung, die sich seiner annimmt.
f :: T σ1 . . . σm -> τ
f (C1 x11 . . . x1n1) = e1
where s11 = f x1l11
. . .
. . .
s1p1 = f x1l1p1 f (Cr xr1 . . . xrnr) = er
where sr1
. . .
= f xrlr1
srpr = f xrlrpr
Der Ausdruck ei darf die Variablen xi1, . . . , xini und die Variablen si1, . . . , sipi enthalten.
Ist pi = 0, so spricht man von einer Rekursionsbasis, sonst von einem Rekursionsschritt.
4.2.4. Verstärkung der Rekursion
Es ist eine gute Idee, als erstes das Schema der strukturellen Rekursion heranzuziehen,
um eine Funktion zu programmieren. Aber nicht immer führt dieser Ansatz zum Erfolg
bzw. nicht immer ist das Ergebnis zufriedenstellend, das man auf diesem Wege erhält.
Schauen wir uns ein Beispiel an: Das Problem lautet, die Reihenfolge der Elemente einer
Liste umzukehren. Wenden wir das Schema der strukturellen Rekursion an, erhalten wir
die folgende oder eine ähnliche Definition.
reverse’ :: [a] -> [a] -- vordefiniert
reverse’ [] = []
reverse’ (a:as) = reverse’ as ++ [a]
Übung 4.5 Welche Funktionen aus den vorangegangenen Kapiteln
sind strukturell rekursiv definiert und welche nicht?

68 4. Programmiermethodik
Mit der Listenkonkatenation wird jeweils das erste Element an die gespiegelte Liste
angehängt; dabei muß die Liste jeweils vollständig durchlaufen werden. Die Tatsache,
daß die geschachtelte Verwendung von (++) sehr rechenintensiv ist, kennen wir bereits
aus Abschnitt 3.4 — in der Tat sind reverse und leaves nah verwandt, es gilt
reverse = leaves . leftist. Wie können wir eine bessere Lösung für reverse systematisch
herleiten? Die grundlegende Idee ist die folgende: Wir programmieren eine
Funktion, die ein schwierigeres Problem lößt als verlangt, aber die es uns erlaubt, den
Rekursionsschritt besser zu bewältigen. Diese Technik nennt man „Verstärkung des Rekursionsschritts“
oder „Programmieren durch Einbettung“. Schauen wir uns die Technik
zunächst am obigen Beispiel an. Im Rekursionsschritt müssen wir die Restliste spiegeln
und an das Ergebnis eine Liste anhängen. Diese Beobachtung führt zu der Idee, eine
Funktion zu programmieren, die beide Aufgaben gleichzeitig löst. Also:
reel :: [a] -> [a] -> [a]
reel x y = reverse x ++ y
Die Spezifikation verkörpert sozusagen den kreativen Einfall. Interessant ist, daß wir die
Definition von reel aus dieser Spezifikation systematisch ableiten können. Anhaltspunkt
für die Fallunterscheidung ist natürlich wieder das Schema der strukturellen Rekursion.
Rekursionsbasis (x = []):
Rekursionsschritt (x = a:as):
reel [] y
= reverse [] ++ y (Spezifikation)
= [] ++ y (Def. reverse)
= y (Def. (++))
reel (a:as) y
= reverse (a:as) ++ y (Spezifikation)
= (reverse as ++ [a]) ++ y (Def. reverse)
= reverse as ++ ([a] ++ y) (Ass. (++))
= reverse as ++ (a:y) (Def. (++))
= reel as (a:y) (Spezifikation)
Somit erhalten wir die folgende Definition von reel:
reel :: [a] -> [a] -> [a]
reel [] y = y
reel (a:as) y = reel as (a:y)
Wenn man sich die rekursiven Aufrufe anschaut, sieht man, daß immer ein Listenelement
vom ersten zum zweiten Parameter „wandert“. Dieser Vorgang begegnet uns im

4.3. Strukturelle Induktion 69
täglichen Leben, wenn wir einen Stapel von Blättern umdrehen: Das oberste Blatt des
Stapels wird auf einen weiteren, anfangs leeren Stapel gelegt; das wiederholen wir solange,
bis der erste Stapel leer ist. Der neue Stapel enthält dann die Blätter in umgekehrter
Reihenfolge.
Die ursprüngliche Funktion, reverse, erhalten wir schließlich durch Spezialisierung
von reel.
reverse’’ :: [a] -> [a]
reverse’’ as = reel as []
Fassen wir zusammen: Die vielleicht überraschende Erkenntnis ist zunächst, daß ein
schwieriges Problem nicht unbedingt auch schwieriger zu lösen ist. Dies liegt im wesentlichen
daran, daß im Rekursionsschritt eine „bessere“ Lösung zur Verfügung steht, die
leichter zu einer Gesamtlösung ausgebaut werden kann. Der kreative Moment liegt in der
Formulierung einer geeigneten Rekursionsverstärkung; eine genaue Analyse, warum der
erste Lösungsansatz scheiterte, liefert dafür in der Regel wichtige Hinweise.
4.3. Strukturelle Induktion
Wir haben bisher das Sortierproblem aus zwei verschiedenen Blickwinkeln betrachtet:
Wir haben das Problem formal spezifiziert und wir haben für das Problem eine Lösung
angegeben. Es ist an der Zeit, die beiden losen Enden wieder zu zusammenzuführen. Wir
werden in diesem Abschnitt zeigen, daß das Sortierprogramme korrekt ist, d.h., daß es die
Spezifikation des Sortierproblems erfüllen. So wie es Programmiermethoden gibt, kennt
man auch Beweismethoden, die uns bei der Programmverifikation unterstützen.
4.3.1. Strukturelle Induktion auf Listen
Das Programm insertionSort sieht richtig aus. Aber, können wir das auch beweisen
— und wenn, dann wie? Es überrascht wahrscheinlich nicht: Der Beweis wird nach einem
ähnlichen Schema geführt, wie wir es für die Programmierung von insertionSort
verwendet haben. Für Listen nimmt das Schema die folgende Form an:
Induktionsbasis ([]): Wir zeigen die Aussage zunächst für die leere Liste [].
Induktionsschritt (a:as): Wir nehmen an, daß die Aussage für die Liste as gilt, und
zeigen, daß sie unter dieser Voraussetzung auch für a:as gilt.
Übung 4.6 Wende die Technik der Rekursionsverstärkung auf
die strukturell rekursive Definition von leaves an.
Lisa Lista: Harry — kannst Du mir erklären, warum die Anwendung
dieser Beweisregel irgendetwas beweist?
Harry Hacker: Nee - habe in der Schule gelernt, das Schlußregeln
so etwas wie Axiome sind, also auf Annahmen oder Absprachen
beruhen. Hat mich nie überzeugt.
Lisa Lista: Ist doch auch albern, oder? Wenn ich eine Aussage
mit Beweisregeln beweise, die selbst nichts als Annahmen sind,
kann ich doch gleich die Aussage als Annahme annehmen.
Prof. Paneau: Ich muß doch sehr um etwas mehr Respekt gegenüber
der Wissenschaftstheorie bitten! In diesem konkreten
Fall aber gebe ich ihnen Recht: Natürlich läßt sich diese Beweisregel
begründen. Man hat damit nämlich eine Konstruktionsvorschrift
angegeben, wie für jede konkrete Liste ein Beweis geführt
werden kann: Man beginnt mit Φ([]), nimmt dann sukzessive die
Listenelemente hinzu und wendet jedesmal den Beweis des Induktionsschritt
an, um zu zeigen, daß auch mit diesem Element
die Aussage noch gilt. Das geht, weil der Induktionsschritt ja
für ein beliebiges Element bewiesen wurde. Was das Induktionsschema
also zeigt, ist, daß man für jede Liste einen Beweis
führen kann — und damit gilt die Aussage Φ natürlich für alle
Listen.
Übung 4.7 Benutze die Erläuterung von Prof. Paneau, um zu erklären,
warum das hier angegebene Schema nicht für den Nachweis
von Eigenschaften unendlicher Listen zu gebrauchen ist.

70 4. Programmiermethodik
Diese Beweisregel kann man formal wie folgt darstellen:
Φ([])
(∀a, as) Φ(as) =⇒ Φ(a:as)
(∀x) Φ(x)
Dabei symbolisiert Φ die Eigenschaft, die wir für alle Listen nachweisen wollen. Über
dem waagerechten Strich werden die Voraussetzungen aufgeführt, unter dem Strich steht
die Schlußfolgerung, die man daraus ziehen kann. Man kann die Regel als Arbeitsauftrag
lesen: Um (∀x) Φ(x) zu zeigen, müssen Φ([] und die Implikation (∀a, as) Φ(as) =⇒
Φ(a:as) nachgewiesen werden. Die im Induktionsschritt getätigte Annahme Φ(as) nennt
man auch Induktionsvoraussetzung; im Beweise notieren wir ihre Anwendung mit dem
Kürzel „I.V.“.
Allgemein gilt, daß sich die Organisation eines Beweises stark an der Organisation der
beteiligten Funktionen orientiert. Also: Die Funktion insertionSort stützt sich auf die
Hilfsfunktion insert ab. Entsprechend weisen wir zunächst die Korrektheit von insert
nach. Hier ist ihre Spezifikation:
ordered x = True =⇒ ordered (insert \(a\) \(x\)) = True (4.7)
bag (insert a x) = a ⊎ bag x (4.8)
Wir verlangen, daß insert a eine geordnete Liste in eine geordnete Liste überführt und
daß insert a x eine Permutation von a:x ist. Beachte, daß Aussage 4.7 eine Vorbedingung
formuliert: "wir weisen die Korrektheit von insert a x nur für den Fall nach,
daß x geordnet ist.
Wir zeigen zunächst Aussage (4.8): Diesen einen Beweis führen wir, ohne etwas auszulassen
oder „mit der Hand zu wedeln“. Es ist ganz nützlich, die Aussage Φ noch einmal
genau aufzuschreiben.
Induktionsbasis (x = []):
Φ(x) ⇐⇒ (∀a) bag (insert a x) = a ⊎ bag x (4.9)
bag (insert a [])
= bag [a] (Def. insert)
= a ⊎ bag [] (Def. bag)
Induktionsschritt (x = a’:as): Im Rumpf von insert wird an dieser Stelle zwischen
zwei Fällen unterschieden, die wir im Beweis nachvollziehen. Fall a

4.3. Strukturelle Induktion 71
Fall a

Übung 4.8 Führe den Korrektheitsbeweis für insertionSort
durch!
Übung 4.9 Zeige die folgenden Eigenschaften mittels Strukturinduktion:
take n x ++ drop n x = x (4.10)
bag (x ++ y) = bag x ⊎ bag y (4.11)
x ++ (y ++ z) = (x ++ y) ++ z .(4.12)
Übung 4.10 Programmiere eine Funktion complete n, die
einen vollständigen Baum der Tiefe n konstruiert.
72 4. Programmiermethodik
Mit Hilfe der eben bewiesenen Hilfssätze können wir uns nun daran machen, die Korrektheit
von insertionSort nachzuweisen. Die Beweise sind allerdings so einfach, daß
wir sie der geneigten Leserin zur Übung überlassen.
Todo: Notation, e1 = e2, insbesondere e1

4.3. Strukturelle Induktion 73
Induktionsbasis (t = Leaf a): analog. Induktionsschritt (t = Br l r): Jetzt können wir
annehmen, daß die Aussage sowohl für l als auch für r gilt.
size (Br l r)
= size l + size r (Def. size)
2ˆdepth l + 2ˆdepth r (I.V.)
2 * 2ˆ(max (depth l) (depth r)) (Eig. max)
= 2ˆ(max (depth l) (depth r) + 1) (Eig. (ˆ))
= 2ˆdepth (Br l r) (Def. depth)
Mit der obigen Formel können wir die Größe nach oben abschätzen. Formen wir die
Ungleichung um, erhalten wir
depth t log 2 (size t) (4.15)
und können die Tiefe nach unten abschätzen. Beide Aussagen werden wir noch häufiger
benötigen.
4.3.3. Das allgemeine Induktionsschema
Nachdem wir zwei Instanzen des Induktionsschemas kennengelernt haben, sind wir (hoffentlich)
fit für das allgemeine Rezept. Wie auch beim allgemeinen Rekursionsschema
ist der Ausgangspunkt die allgemeine Form der Datentypdeklaration, wie wir sie in Abschnitt
3.1.1 kennengelernt haben.
data T a1 . . . am = C1 t11 . . . t1n1
| . . .
| Cr tr1 . . . trnr
Wir müssen wiederum zwischen rekursiven und nicht-rekursiven Konstruktorargumenten
unterscheiden: Seien also li1, . . . , lipi mit 1 li1 < li2 < · · · < lipi ni die Positionen,
an denen der Konstruktor Ci rekursiv ist. Das Induktionsschema besteht nun aus r Prämissen;
für jeden Konstruktor gibt es eine Beweisobligation.
(∀x11 . . . x1n1) Φ(x1l11) ∧ · · · ∧ Φ(x1l1p 1 ) =⇒ Φ(C1 x11 . . . x1n1)
. . .
(∀xr1 . . . xrnr) Φ(xrlr1) ∧ · · · ∧ Φ(xrlrpr ) =⇒ Φ(Cr xr1 . . . xrnr)
(∀x) Φ(x)
Ist pi = 0, so spricht man von einer Induktionsbasis, sonst von einem Induktionsschritt.
Übrigens — die natürliche Induktion, die man aus der Schule kennt (siehe Abschnitt B.3.3),
ist ein Spezialfall der strukturellen Induktion. Um dies zu sehen, muß man nur die natürlichen
Zahlen als Datentyp mit zwei Konstruktoren einführen, etwa
Übung 4.11 Zeige den folgenden Zusammenhang zwischen der
Anzahl der Blätter (size) und der Anzahl der Verzweigungen in
einem Binärbaum (branches, siehe Übung 4.3).
branches t + 1 = size t (4.14)
Übung 4.12 Leite aus dem allgemeinen Induktionsschema eine
Instanz für den Typ Musik ab.
Harry Hacker: Wie rechnet man denn mit diesen Zahlen:
Succ Zero + Succ (Succ Zero) klappt irgendwie nicht.
Lisa Lista: Du mußt eben entsprechende Rechenregeln aufstellen,
z.B. für die Addition zweier Zahlen:
addN :: Natural -> Natural -> Natural
addN Zero n = n
addN (Succ m) n = Succ (addN m n)
Übung 4.13 Hilf Harry bei der Definition der Multiplikation auf
Natural (Hinweis: Kochrezept anwenden).

Übung 4.14 Definiere eine Funktion, die überprüft, ob ein
Baum die Braun-Eigenschaft erfüllt.
74 4. Programmiermethodik
data Natural = Zero | Succ Natural
Die Zahl n schreiben wir damit als n-fache Anwendung von Succ auf Zero: 1 entspricht
Succ Zero, 2 entspricht Succ (Succ Zero) usw. Die Beweisregel für die Natürliche
Induktion nimmt dann die Form der Strukturellen Induktion über dem Typ Natural an:
Φ(Zero)
(∀n) Φ(n) =⇒ Φ(Succ n)
(∀n ∈ Nat) Φ(n)
Die Verallgemeinerung der vollständigen Induktion auf beliebige Datentypen lernen wir
im Vertiefungsabschnitt 4.6 kennen.
4.3.4. Verstärkung der Induktion
Die Formulierung von Rechenregeln und die Formulierung von Beweisen sind zwei sehr
nah verwandte Tätigkeiten. Wir haben versucht, die Zusammenhänge durch den identischen
Aufbau der Abschnitte 4.2 und 4.3 zu verdeutlichen. Entsprechend beschäftigen
wir uns in diesem Abschnitt mit dem beweistheoretischen Analogon zur Rekursionsverstärkung.
Übertragen auf Induktionsbeweise haben wir es mit dem folgenden Phänomen zu tun:
Wir versuchen eine Aussage durch Induktion zu zeigen, bleiben aber im Induktionsschritt
stecken; die Induktionsannahme ist zu schwach, um den Induktionsschritt durchzuführen.
Wir entkommen dem Dilemma, indem wir eine stärkere (schwierigere) Aussage zeigen,
die es uns aber erlaubt, den Induktionsschritt erfolgreich zu absolvieren.
Verdeutlichen wir diese Technik vermittels eines Beispiels: Betrachten wir die Bäume,
die die Funktion build aus Abschnitt 3.4 erzeugt. Es fällt auf, daß die Blätter sich höchstens
auf zwei Ebenen befinden, d.h., die Länge des kürzesten und des längsten Pfades
von der Wurzel bis zu einem Blatt unterscheidet sich höchstens um eins. Für die Spezifikation
dieser Eigenschaft benötigen wir neben depth die Funktion undepth, die die
minimale Tiefe eines Baums bestimmt.
undepth :: Tree a -> Integer
undepth Nil = 0
undepth (Leaf _) = 0
undepth (Br l r) = min (undepth l) (undepth r) + 1
Die Funktion undepth unterscheidet sich von depth nur in der Verwendung von min
statt max. Die Funktion build konstruiert einen Baum, indem sie ⌊n/2⌋ Elemente auf den
linken und ⌈n/2⌉ Elemente auf den rechten Teilbaum verteilt. Bäume mit dieser Knotenverteilung
heißen auch Braun-Bäume: t heißt Braun-Baum, wenn jeder Teilbaum der Form
Br l r die Eigenschaft size r - size l ∈ {0, 1} erfüllt.

4.3. Strukturelle Induktion 75
Die Aussage, die wir zeigen wollen, lautet somit: Sei t ein Braun-Baum, dann gilt
depth t - undepth t ∈ {0, 1} . (4.16)
Führt man für diese Aussage unmittelbar einen Induktionsbeweis durch, scheitert man im
Induktionsschritt: aus den Induktionsvoraussetzungen läßt sich nicht die gewünschte Aussage
herleiten. Man merkt nach einigem Herumprobieren, daß man die Tiefe der Bäume
mit ihrer Größe in Verbindung setzen muß. Konkret: Sei t ein Braun-Baum, dann gilt
2 n size t < 2 n+1
2 n−1 < size t 2 n
=⇒ undepth t = n , (4.17)
=⇒ depth t = n . (4.18)
Ist die Größe einer 2-er Potenz, so ist der Baum vollständig ausgeglichen; alle Blätter
befinden sich auf einer Ebene. Anderenfalls liegt ein Höhenunterschied von eins vor.
Wenden wir uns dem Beweis zu. Induktionsbasis (t = Nil): Die Aussage folgt direkt
aus size Nil = 1 und undepth Nil = depth Nil = 0. Induktionsbasis (t =
Leaf a): analog. Induktionsschritt (t = Br l r): Da t ein Braun-Baum ist, gilt size l =
size t⌉. Damit folgt für den linken Teilbaum
⌊ 1
1
2size t⌋ und size r = ⌈ 2
und entsprechend für den rechten
Insgesamt erhalten wir
2 n size t < 2 n+1
=⇒ 2 n−1 size l < 2 n
=⇒ undepth l = n − 1 (I.V.)
2 n size t < 2 n+1
=⇒ 2 n−1 size r 2 n
=⇒ undepth r n − 1 (I.V.)
undepth (Br l r)
(Arithmetik)
(Arithmetik)
= min (undepth l) (undepth r) + 1 (Def. undepth)
= n (obige Rechnungen)
Die Aussage für depth zeigt man analog.
Die ursprüngliche Behauptung ergibt sich als einfache Folgerung aus dieser Eigenschaft.
Wir sehen: Die schwierigere Aussage ist einfacher nachzuweisen als die ursprüngliche.
Denn: im Induktionsschritt können wir auf stärkeren Voraussetzungen aufbauen. Aber:
die Formulierung der Induktionsverstärkung erfordert auch eine tiefere Durchdringung
des Problems. Der entscheidende Schritt war hier, die minimale und maximale Tiefe nicht
nur zueinander, sondern zur Größe in Beziehung zu setzen.

[8, 3, 5]
[3, 5, 8]
[8, 3, 5, 3, 6, 1]
[3, 5]
8 3 5 3 6 1
[3, 5]
[1, 3, 3, 5, 6, 8]
[3, 6, 1]
[6, 1]
[1, 6]
[1, 3, 6]
Abbildung 4.1: Sortieren durch Fusionieren
Harry Hacker: Was bedeutet denn der Punkt in der Definition
von mergeSort?
Grit Garbo: Den mißglückten Versuch, die Komposition von
Funktionen zu notieren . . .
Lisa Lista: Ich hab mal nachgeschlagen: der Punkt ist so definiert:
(.) :: (b -> c) -> (a -> b) -> (a -> c)
(f . g) a = f (g a)
Nichts Aufregendes, verdeutlicht vielleicht besser die Unterteilung
in zwei Phasen.
76 4. Programmiermethodik
4.3.5. Referential transparency
Gleichungslogik, Gesetz von Leibniz, Vergleich zu Pascal (x ++ x mit Seiteneffekten).
4.4. Anwendung: Sortieren durch Fusionieren
Kommen wir noch einmal auf das Sortierproblem zurück. Der in Abschnitt 4.2.1 entwickelte
Algorithmus „Sortieren durch Einfügen“ wird häufig von Hand beim Sortieren von
Spielkarten verwendet. Man kann natürlich auch anders vorgehen, insbesondere wenn es
Helfer gibt: Der Kartenstapel wird halbiert, beide Hälften werden getrennt sortiert und
anschließend werden die beiden sortierten Teilstapel zu einem sortieren Gesamtstapel fusioniert.
Das Sortieren der Hälften kann unabhängig voneinander und insbesondere nach
dem gleichen Prinzip durchgeführt werden.
Typisch für dieses Verfahren ist die (gedankliche) Unterteilung in zwei Phasen: In der
ersten Phase wird jeder Stapel wiederholt halbiert, bis sich entweder keine Helfer mehr
finden oder der Stapel nur noch aus einer Karte besteht. In der zweiten Phase werden die
einzelnen Teilstapel wieder zusammengeführt, bis zum Schluß ein sortierter Stapel übrigbleibt.
In Abbildung 4.1 wird das Verfahren exemplarisch für die Liste [8, 3, 5, 3, 6, 1]
vorgeführt. Man sieht sehr schön die beiden Phasen des Verfahrens: in der oberen Hälfte
der Abbildung wird geteilt, in der unteren wird zusammengeführt.
Betrachtet man die Graphik in Abbildung 4.1 genauer, so entdeckt man, daß die obere
Hälfte gerade einem Binärbaum entspricht — wenn man von den redundanten Beschriftungen
der Verzweigungen absieht. Und: wir haben die erste Phase bereits in Abschnitt
3.4 unter dem Namen build programmiert. Nennen wir die zweite Phase sortTree,
dann erhalten wir
mergeSort :: (Ord a) => [a] -> OrdList a
mergeSort = sortTree . build
Das Sortierverfahren „Sortieren durch Fusionieren“ ist nach der zentralen Operation der
zweiten Phase, dem Fusionieren zweier geordneter Listen (engl. merge), benannt. 2
4.4.1. Phase 2: Sortieren eines Binärbaums
Für die Definition von sortTree verwenden wir — wie nicht anders zu erwarten — das
Schema der strukturellen Rekursion auf Bäumen.
2 In der Literatur wird „merge“ häufig und schlecht mit Mischen übersetzt. Unter dem Mischen eines Kartenspiels
versteht man freilich eher das Gegenteil.

4.4. Anwendung: Sortieren durch Fusionieren 77
sortTree :: (Ord a) => Tree a -> OrdList a
sortTree Nil = []
sortTree (Leaf a) = [a]
sortTree (Br l r) = merge (sortTree l) (sortTree r)
Im Rekursionsschritt müssen zwei bereits geordnete Listen zu einer geordneten Liste fusioniert
werden. Die Funktion merge, die sich dieser Aufgabe annimmt, läßt sich ebenfalls
strukturell rekursiv definieren.
merge :: (Ord a) => OrdList a -> OrdList a -> OrdList a
merge [] bs = bs
merge (a:as) [] = a:as
merge (a:as) (b:bs)
| a OrdList a -> OrdList a ->
OrdList a
merge’ [] = id
merge’ (a:as) = insert
where
insert [] = a:as
insert (b:bs)
| a Bag a
bag Nil = ∅
bag (Leaf a) = a
bag (Br l r) = bag l ⊎ bag r

Übung 4.16 Zeige, daß sortTree ihre Spezifikation erfüllt.
78 4. Programmiermethodik
Wir verwenden bag im folgenden sowohl auf Listen als auch auf Bäumen. Das Phänomen
der Überladung — die Verwendung des gleichen Namens für unterschiedliche, aber verwandte
Funktionen — kennen wir bereits von unserem Haskell: (==) verwenden wir auf
allen Typen, die in der Typklasse Eq enthalten sind.
Für die Funktion build muß gelten:
bag (build x) = bag x (4.22)
Beachte, daß die Struktur des generierten Baums für den Nachweis der Korrektheit keine
Rolle spielt. Beim Nachweis der obigen Aussage versagt das Schema der strukturellen
Induktion: die Funktion build selbst verwendet ein allgemeineres Rekursionsschema,
das wir in Abschnitt 4.5 näher untersuchen. Das beweistheoretische Analogon besprechen
wir im Vertiefungsabschnitt 4.6, so daß wir der Aussage an dieser Stelle einfach Glauben
schenken.
Für sortTree muß schließlich gelten:
ordered (sortTree \(t\)) (4.23)
bag (sortTree t) = bag t (4.24)
Beide Aussagen lassen sich mit dem Induktionsschema für Tree einfach nachweisen
(siehe Aufgabe 4.16).
Wir haben kurz angemerkt, daß für den Nachweis der Korrektheit die Struktur des in
der ersten Phase erzeugten Baums keine Rolle spielt. Natürlich können wir mit leftist
bzw. rightist auch einen „Strunk“ erzeugen. Wir erhalten dann:
insertionSort’ :: (Ord a) => [a] -> OrdList a
insertionSort’ = sortTree . rightist
4.4.2. Phase 1: Konstruktion von Braun-Bäumen
Wir haben in Abschnitt 4.3.4 besprochen, daß die Funktion build sogenannte Braun-
Bäume konstruiert. Zur Erinnerung: der linke und der rechte Teilbaum sind jeweils gleich
groß, vorausgesetzt die Gesamtzahl der Blätter ist gerade; anderenfalls ist der rechte Teilbaum
ein Element größer. Die beiden Varianten von build, die wir in Abschnitt 3.4
vorgestellt haben, sind beide nicht strukturell rekursiv definiert — sie implementieren die
Idee des wiederholten Halbierens der Ausgangsliste sehr direkt und natürlich.
In diesem Abschnitt wollen wir der — vielleicht akademisch anmutenden — Frage nachgehen,
wie sich Braun-Bäume strukturell rekursiv erzeugen lassen. Aus dem Rekursionsschema
ergibt sich mehr oder minder zwangsläufig die folgende Definition.
type Braun a = Tree a

4.4. Anwendung: Sortieren durch Fusionieren 79
build’ :: [a] -> Braun a
build’ [] = Nil
build’ (a:as) = extend a (build as)
Im Rekursionsschritt stellt sich eine interessante Teilaufgabe: ein Braun-Baum muß um
ein Element erweitert werden. Die Basisfälle sind schnell gelöst:
extend :: a -> Braun a -> Braun a
extend a Nil = Leaf a
extend a (Leaf b) = Br (Leaf b) (Leaf a)
Im Rekursionsschritt haben wir einen Baum der Form Br l r mit size r - size l ∈
{0, 1} gegeben, der um ein Element erweitert werden muß. Interessanterweise ergibt sich
das weitere Vorgehen zwangsläufig: Das Element a muß in den kleineren Teilbaum, also
l, eingefügt werden; da der erweiterte Baum extend a l größer ist als r, müssen wir
die beiden Teilbäume zusätzlich vertauschen. Anderenfalls wäre die Braun-Eigenschaft
verletzt. Wir erhalten:
extend a (Br l r) = Br r (extend a l)
Diese Vorgehensweise ist typisch für Operationen auf Braun-Bäumen. Trotz der knappen
Definition von extend erfordert es einige Kopfakrobatik, die Konstruktion größerer
Bäume nachzuvollziehen. In Abbildung 4.2 sind die Bäume dargestellt, die man erhält,
wenn man nacheinander 0, 1, . . . , 7 in den anfangs leeren Baum einfügt. Beachte, daß
build’ die Elemente anders auf die Blätter verteilt als die Funktionen gleichen Namens
aus Abschnitt 3.4.
Kommen wir zur Korrektheit der Operationen: Zunächst haben wir die übliche Forderung
nach dem „Erhalt der Elemente“:
bag (extend a t) = a ⊎ bag t (4.25)
bag (build x) = bag x (4.26)
Zusätzlich müssen build und extend Braun-Bäume erzeugen:
braun t =⇒ braun (extend a t) (4.27)
braun (build x) (4.28)
Genau wie bei insert und merge geben wir auch bei extend eine Vorbedingung an:
wir weisen die Korrektheit von extend a t nur für den Fall nach, daß t ein Braun-Baum
ist.
0 0 1
1
0 2 0 2 1 3
1 3 2
(a) (b) (c) (d) (e)
2
0 4
3
1 5
3
1 5 0 4 2 6
(f) (g)
0 4 2 6 1 5 3 7
(h)
Abbildung 4.2: Braun-Bäume der Größe 1 bis 8
0 4
Übung 4.17 Zeige die Korrektheit von build und extend. Ist
die Spezifikation der Funktionen eindeutig?

80 4. Programmiermethodik
4.5. Wohlfundierte Rekursion
4.5.1. Das Schema der wohlfundierten Rekursion
Nicht alle rekursiven Funktionen, die wir bisher kennengelernt haben, verwenden das
Schema der strukturellen Rekursion. Ausnahmen sind power (Abschnitt 3.2.3), leaves’,
build und buildSplit (alle Abschnitt 3.4). Schauen wir uns noch einmal die Definition
von build an.
build :: [a] -> Tree a
build [] = Nil
build [a] = Leaf a
build as = Br (build (take k as)) (build (drop k as))
where k = length as ‘div‘ 2
In der dritten Gleichung wird die Argumentliste halbiert und die rekursiven Aufrufe
erfolgen auf den beiden Hälften. Strukturelle Rekursion liegt nicht vor, da take n as
keine Unterstruktur von as ist (wohl aber drop k as). Die Funktion ist trotzdem wohldefiniert,
da die Länge der Teillisten echt kleiner ist als die Länge der Argumentliste. Die
rekursiven Aufrufe erhalten somit immer kleinere Listen, bis irgendwann der einfache Fall
der höchstens einelementigen Liste erreicht ist. Daß der einfache Fall erreicht wird, ist so
sicher wie das Amen in der Kirche: Man sagt, die Rekursion ist wohlfundiert.
Im Gegensatz zur strukturellen Rekursion kann das Schema der wohlfundierten Rekursion
universell für beliebige Datentypen verwendet werden. Hier ist das Kochrezept:
Ist das Problem einfach, wird es mit ad-hoc Methoden gelöst. Anderenfalls
wird es in einfachere Teilprobleme aufgeteilt, diese werden nach dem gleichen
Prinzip gelöst und anschließend zu einer Gesamtlösung zusammengefügt.
Das Rekursionsschema heißt manchmal auch etwas kriegerisch „Teile und Herrsche“-
Prinzip. Betrachten wir noch einmal die oben erwähnten Funktionen: Die Funktion build
unterteilt ein Problem in zwei Teilprobleme; dies ist häufig der Fall, muß aber nicht so
sein. Die Funktionen power und leaves enthalten lediglich einen rekursiven Aufruf. Daß
die rekursiven Aufrufe tatsächlich „einfachere“ Probleme bearbeiten, ist bei allen Funktionen
— mit Ausnahme von leaves — einsichtig. Im Fall von leaves geht der Baum
Br (Br l’ r’) r in den Baum Br l’ (Br r’ r) über. Inwiefern ist der zweite Baum
einfacher als der erste? Die Anzahl der Blätter wird zum Beispiel nicht geringer.
Damit die Rekursion wohlfundiert ist, müssen die Argumente der rekursiven Aufrufe
stets kleiner werden. Und: der Abstieg über immer kleiner werdende Elemente muß irgendwann
auf einen Basisfall zulaufen. Diese Eigenschaft muß man als Programmiererin
nachweisen; sie wird einem nicht durch das Rekursionsschema geschenkt. Im Gegenteil:

4.5. Wohlfundierte Rekursion 81
der Nachweis der Wohlfundiertheit ist Voraussetzung für die sinnvolle Anwendung des
Schemas.
Formal zeigen wir diese Voraussetzung durch die Angabe einer wohlfundierten Relation:
Die Relation „≺“ heißt wohlfundiert, wenn es keine unendliche absteigende Kette
· · · ≺ xn ≺ · · · ≺ x2 ≺ x1
gibt. Beispiele für wohlfundierte Relationen sehen wir in Kürze; ein Gegenbeispiel stellt
die Relation „

82 4. Programmiermethodik
das Gewicht eines Baums um eins: Ein schwarzer wird zu einem weißen Knoten (Abbildung
4.4). Die Relation „≺“ wird somit definiert durch
t ≺ u ⇐⇒ weight t < weight u .
Überzeugen wir uns, daß das Gewicht des rekursiven Aufrufs tatsächlich kleiner wird.
weight (Br (Br l’ r’) r)
= 2*size (Br l’ r’) + weight r - 1 (Def. weight)
= 2*size l’ + 2*size r’ + weight r - 1 (Def. size)
> 2*size l’ + 2*size r’ + weight r - 2 (Arithmetik)
= 2*size l’ + weight (Br r’ r) - 1 (Def. weight)
= weight (Br l’ (Br r’ r)) (Def. weight)
Damit ist gezeigt, daß leaves wohlfundiert ist.
Übrigens — die strukturelle Rekursion ist ein Spezialfall der wohlfundierten Rekursion.
Die Relation ≺ liegt bei der strukturellen Rekursion implizit zugrunde: y ≺ x ⇐⇒
y ist Substruktur von x. Dieser Zusammenhang macht auch einen Vorzug der strukturellen
Rekursion deutlich: wir bekommen den Nachweis der Wohlfundiertheit geschenkt.
4.6. Vertiefung: Wohlfundierte Induktion
Der Beweis von Aussage 4.22 steht noch aus. Daß build x und x stets die gleichen
Elemente enthalten, läßt sich nicht — oder jedenfalls nicht direkt — mit struktureller Induktion
beweisen. Dies liegt im wesentlichen daran, daß build das Schema der wohlfundierten
Rekursion verwendet. Glücklicherweise gibt es aber auch ein korrespondierendes
Beweisschema, daß es uns erlaubt, den Beweis direkt zu führen.
Wie auch beim Rekursionsschema muß zunächst eine wohlfundierte Relation festgelegt
werden, die beschreibt, was unter „einfacher“ bzw. „kleiner“ zu verstehen ist. Das Schema
der wohlfundierten Induktion nimmt dann die folgende Form an:
Wir zeigen die Aussage für alle Elemente, jeweils unter der Voraussetzung, daß
die Aussage für alle kleineren Elemente wahr ist.
Die formale Definition macht die Beweis-Obligation deutlich:
(∀y) ((∀z ≺ y) Φ(z)) =⇒ Φ(y)
(∀x) Φ(x)
Im Unterschied zur strukturellen Induktion gibt es keine explizite Induktionsbasis und
keinen Induktionsschritt: Die Aussage Φ(y) muß für alle y gezeigt werden, jeweils unter

4.6. Vertiefung: Wohlfundierte Induktion 83
der Annahme, daß Φ(z) für alle z ≺ y gilt. Um diese Allaussage nachzuweisen, wird
man in der Regel eine Fallunterscheidung über die Elemente des beteiligten Datentyps
vornehmen. Ist die Prämisse (∀z ≺ y) Φ(z) leer, d.h., es gibt keine kleineren Elemente als
y, dann liegt implizit ein Basisfall vor. Übung 4.19 Zeige, daß power korrekt ist.
Wenden wir uns dem Nachweis von 4.22 zu: Die Relation „≺“ ist wie in 4.29 definiert,
d.h., wir führen den Beweis über die Länge von x. Für die Fälle x = [] und x = [a] ist
die Aussage wahr. In allen anderen Fällen gilt 1 k < length x. Daraus folgt
length (take k x) = k < length x
length (drop k x) = length x - k
< length x.
Somit kann die Induktionsannahme für die Argumente von build angewendet werden.
Wir erhalten:
bag (build x)
= bag (Br (build (take k x)) (build (drop k x))) (Def. build)
= bag (build (take k x)) ⊎ bag (build (drop k x)) (Def. bag)
= bag (take k x) ⊎ bag (drop k x) (I.V.)
= bag (take k x ++ drop k x) (4.11)
= bag x (4.10)
Übung 4.20 Zeige
bag (leaves t) = bag t (4.30)
mittels wohlfundierter Rekursion.
Übung 4.21 Zeige 4.30 mittels struktureller Induktion.

84 4. Programmiermethodik

5. Effizienz und Komplexität
Ziele des Kapitels:
Jeder von uns hat schon manches Mal eine Rechnung abgebrochen — weil uns die Anzahl
der Rechenschritte zu groß wurde oder uns die Unhandlichkeit eines immer größer
wachsenden Formelberges entmutigt hat. Für uns ist dies immer der Anstoß, einen geschickteren
Lösungsweg zu suchen (oder jemand anders, der die Rechnung durchführt).
Niemand würde deshalb auf die Idee kommen, eine allgemeine Theorie des Rechenaufwands
zu entwickeln. Anders liegt die Sache, wenn wir umfangreiche Rechnungen auf
den Computer übertragen. Denn mit gegebenem Programm liegt ja der Lösungsweg fest
— und damit auch der zugehörige Rechenaufwand. Die Frage nach der Effizienz von Programmen
kommt damit auf den Tisch.
Dieser Frage ist ein ganzes Teilgebiet der Informatik gewidmet — die Komplexitätstheorie.
Die Beurteilung der Effizienz von Programmen ist für sie nur der Ausgangspunkt.
Darüber hinaus geht es in ihr um die allgemeinere Frage, mit welchem Aufwand sich
welche Klassen von Problemen algorithmisch lösen lassen.
Von dieser Theorie behandeln wir hier im wesentlichen nur die Ausgangsfrage, nämlich
die Effizienzbeurteilung von Programmen. Die dabei benutzten Begriffe und Techniken
gehören zum elementaren Handwerkszeug jeden Informatikers. Über den Bedarf
eines Programms an Rechenzeit und Speicherplatz sollte man sich klar sein, bevor man
ein Programm startet. Im allgemeinen möchten wir ja auch den Computer nicht unnötig
beschäftigen.
5.1. Grundlagen der Effizienzanalyse
5.1.1. Maßeinheiten für Zeit und Raum beim Rechnen
Zeit mißt man in Sekunden, Raum in Metern. Beides taugt natürlich nicht, wenn wir den
Aufwand zur Durchführung eines Programms messen wollen. Sekunden eignen sich nicht
zur Bestimmung der Rechenzeit — verschiedene Rechner, elektronische wie menschliche,
werden ein unterschiedliches Tempo an den Tag legen, was aber nichts mit den Eigenschaften
des gerechneten Programms zu tun hat. Gleiches gilt für den Platzbedarf beim
Rechnen. Wir können schlecht die Quadratmeter Papier zählen, die im Zuge einer Rechnung
mit Formeln vollgekritzelt werden. Menschliche Rechner weisen enorme Unterschie-

Grit Garbo: In der Tat gelingt es mir stets, auch die komplizierteste
Rechnung auf einer DIN A4 Seite unterzubringen. Tafelwi-
86 5. Effizienz und Komplexität
de im Papierverbrauch auf, ohne daß dies als Problem gesehen wird. Dagegen gleicht der
Tafelanschrieb eines Dozenten schon eher einem bewußten Magagement von begrenzten
Platzressourcen und damit dem, was auch beim maschinellen Rechnen mit beschränktem
Speicherplatz berücksichtigt werden muß. Es gilt also, Maßeinheiten für Rechenzeit und
schen vermeide ich grundsätzlich. Platzbedarf festzulegen, die vom ausführenden Organ unabhängig sind und so nur die
Eigenschaften des Programms wiedergeben.
Ein etwas abstrakteres Maß der Rechenzeit ist ein Rechenschritt. Dabei gibt es verschiedene
Möglichkeiten, was man als einen Rechenschritt zählen will, und wir wählen
die naheliegendste: Ein Rechenschritt ist die Anwendung einer definierenden Gleichung.
Ist die Gleichung bewacht, zählen die Rechenschritte zur Auswertung der Wächter plus
Lisa Lista: Dabei gibt es doch sehr einfache und beliebig komplizierte
Gleichungen, und z.B. die Anwendung der let-Regel
kommt mir ganz besonders aufwendig vor. Wenn von all dem
abstrahiert wird — wie können wir dann ein realistisches Effizienzmaß
erhalten?
Harry Hacker: Mit Maschineninstruktionen und Bytes als Einheiten
für Zeit und Platz wäre mir wohler. Da weiß man was
man hat.
Lisa Lista: Konkreter wär’s allemal, Harry, aber wir müßten die
Haskell-Programme erst in Maschinenbefehle übersetzen, ehe
wir sie beurteilen können...
ein extra Schritt zur Auswahl der rechten Seite. Wenn unsere Programme let-, caseoder
Funktionsausdrücke enthalten, zählen wir auch die Anwendung jeder let-, case-
oder β-Regel als einen Schritt. Was wir nicht zählen, ist die Anwendung eines Kon-
struktors auf seine Argumente — schließlich sind Formeln, soweit sie aus Konstruktoren
aufgebaut sind, ja bereits ausgerechnet.
Im Hinblick auf den Platzbedarf einer Rechnung müssen wir zuächst festlegen, was die
Größe einer Formel ist. Sie soll bestimmt sein durch die Anzahl ihrer Symbole (Funktionen,
Konstruktoren, Variablen). Klammern zählen wir nicht mit. Eine Rechnung geht von
einer gegebenen Formel aus, die es auszuwerten gilt. Als Platzbedarf der Rechnung, in
deren Verlauf eine Formel ja wachsen und wieder schrumpfen kann, betrachten wir die
maximale Formelgröße, die in der Rechnung auftritt. Dies entspricht also eher dem Modell
des Tafelanschriebs mit Löschen erledigter Rechnungsteile (und Wiederverwendung
der Tafelfläche), und weniger dem verschwenderischen Papierverbrauch.
Es ist offensichtlich, daß wir uns bei der Festlegung der Einheiten an den Gegebenheiten
der Sprache Haskell orientiert haben. Will man Programme in anderen Sprachen
beurteilen, kann man in ganz analoger Weise vorgehen. Die Techniken, die wir nun kennenlernen,
sind auf alle Programmiersprachen anwendbar.
5.1.2. Detaillierte Analyse von insertionSort
Wir haben zwei Sortierprogramme kennengelernt. Da beide korrekt sind, realisieren sie
die gleiche mathematische Funktion: isort = mergeSort. Während der Mathematiker
jetzt verschnauft, fängt für den Informatiker die Arbeit an: Es gilt die von den beiden Programmen
benötigten Resourcen, Rechenzeit und Speicherplatz, zu bestimmen. Wenn wir
das erreicht haben, werden wir sehen, daß mergeSort in den meisten Fällen kostengünstiger
arbeitet als isort und somit bei Anwendungen den Vorzug erhält.
Es ist nützlich sich eine Notation für die Bestimmung des Rechenaufwands auszudenken:
T ime(e ⇒ v) bezeichnet die Anzahl der Rechenschritte, um den Ausdruck e zum
Wert v auszurechnen. Sind wir an v nicht interessiert, schreiben wir auch kurz T ime(e).

5.1. Grundlagen der Effizienzanalyse 87
Den Platzbedarf, um e zu v auszurechnen, bezeichnen wir entsprechend mit Space(e ⇒ v)
oder kurz mit Space(e).
Nähern wir uns dem Thema langsam und versuchen eine Analyse des Zeitbedarfs von
isort — der Platzbedarf ist weniger interessant, wie wir später sehen werden. Die Funktion
isort stützt sich auf die Funktion insert ab; also beginnen wir mit der Analyse
von insert. Um die genaue Anzahl der Rechenschritte zu bestimmen, schreiben wir die
Definition von insert noch einmal auf.
insert a [] = [a] (insert.1)
insert a (a’:as) (insert.2)
| a

88 5. Effizienz und Komplexität
Die Gleichungen beschreiben unser bisheriges Wissen über die Funktion T ime. Sie reichen
aus, um z.B. T ime(isort [8,3,5,3,0,1]) zu bestimmen. [Was kommt heraus?]
Das ist nett, stellt uns aber nicht zufrieden: In der Regel wird man die Rechenzeit nicht
für ein bestimmtes Argument, sondern für beliebige Eingaben, d.h. in Abhängigkeit von
der Eingabe, bestimmen wollen. Und: Die Abhängigkeit der Laufzeit von der Eingabe
soll möglichst griffig dargestellt werden. Schließlich wollen wir ja die Effizienz eines Programms
insgesamt bewerten und mit der Effizienz anderer Programme vergleichen. Nun
besteht aber wenig Aussicht, T ime(isort [a1,...,an]) mit einer geschlossenen Formel
auszudrücken. Wir vereinfachen uns das Leben, indem wir etwas abstrahieren und die
Rechenzeit in Abhängigkeit von der Größe der Eingabe bestimmen, d.h., wir kümmern uns
nicht um die Elemente der zu sortierenden Liste, sondern nur um ihre Länge. Eigentlich
ist dies auch vernünftig, da wir in der Regel eher genaue Kenntnis über die Anzahl denn
über die Ausprägung von Daten haben.
Nun ist die Laufzeit von isort nicht funktional abhängig von der Größe der Liste:
isort [1,2,3] ist schneller ausgerechnet als isort [3,2,1]. Wir helfen uns, indem
wir eine obere und eine untere Schranke für die Rechenzeit bestimmen und die Rechenzeit
auf diese Weise einkreisen. In anderen Worten: Wir fragen, wie schnell kann man
isort [a1,...,an] im besten und im schlechtesten Fall ausrechnen. Wenn wir das
Rechnen anderen — z.B. einem Rechner — überlassen, sagt uns die obere Schranke, ob
es sich lohnt, auf das Ergebnis der Rechnung zu warten. Die untere Schranke hilft uns
bei der Entscheidung, ob wir vorher einen Kaffee trinken gehen. Formal suchen wir zwei
Funktionen T isort und T isort, die die Rechenzeit einkreisen:
T isort (n) T ime(isort [a1,...,an]) T isort(n)
Die untere und die obere Schranke sollten natürlich möglichst exakt sein:
T isort (n) = min{ T ime(isort x) | length x = n }
T isort(n) = max{ T ime(isort x) | length x = n }
Daß wir mit der Größe der Eingabe ausgedrückt als natürliche Zahl arbeiten, hat einen
weiteren nicht zu unterschätzenden Vorteil: Wir sind gewohnt mit Funktionen auf N zu
rechnen und von Seite der Mathematik werden wir kräftig unterstützt.
Aus den obigen Gleichungen für T ime können wir Gleichungen für T isort und T isort
ableiten, indem wir annehmen, daß der Wächter in insert immer zu True oder immer

5.1. Grundlagen der Effizienzanalyse 89
zu False auswertet.
T insert (0) = 1
T insert (n + 1) = 3
T insert(0) = 1
T insert(n + 1) = 3 + T insert(n)
T isort (0) = 1
T isort (n + 1) = 1 + T insert (n) + T isort (n)
T isort(0) = 1
T isort(n + 1) = 1 + T insert(n) + T isort(n)
Aus den rekursiven Gleichungen für insert und isort erhalten wir rekursiv definierte
Kostenfunktionen. In der Literatur heißen solche Gleichungen auch Rekurrenzgleichungen,
da die definierte Funktion auf der rechten Seite wieder auftritt (lat. recurrere). In den
folgenden Abschnitten werden wir Techniken kennenlernen, um diese und etwas kompliziertere
Rekurrenzgleichungen aufzulösen. Für den Moment begnügen wir uns damit, die
geschlossenen Formen der Kostenfunktionen anzugeben:
T insert (0) = 1
T insert (n + 1) = 3
T insert(n) = 3n + 1
T isort (0) = 1
T isort (n + 1) = 4n + 1
T isort(n) = (3/2)n 2 + (1/2)n + 1
Im besten Fall muß insert das Element an den Anfang der Liste setzen, im schlechtesten
Fall an das Ende der Liste; die Anzahl der Rechenschritte ist dann proportional zur Länge
der Liste. Sortieren durch Einfügen liebt somit aufsteigend sortierte Listen und verabscheut
absteigend sortierte Listen. Bevor wir zur Analyse der Sortierfunktion mergeSort
kommen, stellen wir ein paar allgemeine Betrachtungen an.
5.1.3. Asymptotische Zeit- und Platzeffizienz
In unseren bisherigen Überlegungen paßt etwas nicht zusammen: Einerseits, um die Kostenfunktionen
zu ermitteln, haben wir recht pedantisch die Rechenschritte gezählt. Andererseits,
bei der Bestimmung der Einheit „Rechenschritt“ haben wir großzügig jede Regel
mit Kosten von eins belegt. Tatsächlich könnte es aber sein, daß die case-Regel aufwendiger
ist als die let-Regel; die Kosten für die let-Regel könnten abhängen von der
Anzahl der Hilfsdefinitionen. Die Anwendung einer definierenden Gleichung könnte von

90 5. Effizienz und Komplexität
der Anzahl der Parameter und von der Größe der Muster abhängen. Zudem war die Einheit
Rechenschritt selbst schon eine Abstraktion von realer, zum Rechnen benötigter Zeit:
Auf dem Rechner Warp III mit dem Übersetzer Turbo-Haskell könnten die Programme
um den Faktor 10 schneller ablaufen als auf dem Rechner Slack I mit dem Übersetzer
Tiny-Haskell. Jede dieser Überlegungen könnte dazu führen, daß die errechneten Kosten
um einen konstanten Faktor verringert oder vergrößert werden müssen.
Die gleiche etwas abstraktere Sichtweise wenden wir auch die Kostenfunktionen an.
Wenn wir die Effizienz eines Programms beurteilen bzw. zwei Programme bezüglich ihrer
Effizienz vergleichen, werden wir zunächst nicht danach fragen, ob 3n2 oder 15n2 Rechenschritte
benötigt werden. Für eine erste Einordnung interessiert uns das asymptotische
Wachstum der Kostenfunktionen: Wie verhält sich die Rechenzeit, wenn die Eingaben
groß — sehr groß — werden. Ein Programm mit einer Rechenzeit von 15n2 is asymptotisch
besser als ein anderes mit einer Rechenzeit von 1
15n3 : Die kleinere Konstante ist für
n 152 = 225 vom höheren Exponenten aufgebraucht.
Um das asymptotische Verhalten von Funktionen zu beschreiben, gibt es einige wichtige
Notationen, die wir im folgenden einführen. Zu einer gegebenen Funktion g : N → N
bezeichnet Θ(g) die Menge aller Funktionen mit der gleichen Wachstumsrate wie g:
Θ(g) = { f | (∃n0, c1, c2)(∀n n0) c1g(n) f(n) c2g(n) } (5.1)
Ist f ∈ Θ(g), so heißt g asymptotische Schranke von f. Funktionen werden in diesem
Zusammenhang überlicherweise durch Ausdrücke beschrieben: 15n 2 meint die Funktion
n ↦→ 15n 2 . Welche Variable die Rolle des formalen Parameters übernimmt, ergibt sich aus
dem Kontext. 1 Wenn wir somit kurz 15n 2 ∈ Θ(n 2 ) schreiben, meinen wir, daß g mit g(n) =
n 2 eine asymptotische Schranke von f mit f(n) = 15n 2 ist. Das asymptotische Verhalten
der Kostenfunktionen von insert und isort können wir wie folgt beschreiben:
T insert (n) ∈ Θ(1)
T insert(n) ∈ Θ(n)
T isort (n) ∈ Θ(n)
T isort(n) ∈ Θ(n 2 )
Wir sagen, die „best case“-Laufzeit von isort ist Θ(n) und die „worst case“-Laufzeit ist
Θ(n 2 ). Man sieht, daß Konstanten und kleine Terme, z.B. 2n + 1 in 3n 2 + 2n + 1, unter den
Tisch fallen. Geht n gegen unendlich, dominiert der Term mit dem größten Exponenten.
1 In unserer Programmiersprache unterscheiden wir sorgfältig zwischen Ausdrücken, die Zahlen bezeichnen,
und Ausdrücken, die Funktionen bezeichnen: 15*nˆ2 ist eine Zahl, die wir ausrechnen können, wenn wir
n kennen. Wollen wir ausdrücken, daß 15*nˆ2 eine Funktion in n ist, schreiben wir \n -> 15*nˆ2. Aus
Gründen der Bequemlichkeit — eine Bequemlichkeit, die uns ein Rechner nicht gestattet — verwenden wir
an dieser Stelle für Funktionen einfach Ausdrücke, ohne den formalen Parameter explizit zu kennzeichnen.

5.1. Grundlagen der Effizienzanalyse 91
Um nicht immer auf die Definition von Θ zurückgreifen zu müssen, ist es nützlich, sich
ein paar Eigenschaften von Θ zu überlegen. Hier ist eine Liste der wichtigsten:
f ∈ Θ(f) (Reflexivität) (5.2)
f ∈ Θ(g) ∧ g ∈ Θ(h) ⇒ f ∈ Θ(h) (Transitivität) (5.3)
f ∈ Θ(g) ⇒ g ∈ Θ(f) (Symmetrie) (5.4)
cf ∈ Θ(f) (5.5)
n a + n b ∈ Θ(n a ) für a > b (5.6)
log a n ∈ Θ(log b n) (5.7)
In der letzten Beziehung haben wir unsere Notation stillschweigend auf Funktionen über
R ausgedehnt. Das erlaubt es uns, ohne „floor“- und „ceiling“-Funktionen zu rechnen.
Neben exakten asymptotischen Schranken gibt es auch Notationen für untere und obere
asymptotische Schranken:
Ω(g) = { f | (∃n0, c)(∀n n0) cg(n) f(n) } (5.8)
O(g) = { f | (∃n0, c)(∀n n0) f(n) cg(n) } (5.9)
Ist f ∈ Ω(g), so heißt g untere asymptotische Schranke von f. Für f ∈ O(g) heißt g entsprechend
obere asymptotische Schranke von f. Die asymptotische Laufzeit von isort
ist z.B. Ω(n) und O(n 2 ). Etwas Vorsicht ist bei der Verwendung von Ω und O geboten.
Auch die folgende Aussage ist wahr: Die asymptotische Laufzeit von isort ist Ω(log n)
und O(n 10 ). Die Schranken müssen eben nicht genau sein. Aus diesem Grund ist es besser
zu sagen: Die „best case“-Laufzeit von isort ist Θ(n) und die „worst case“-Laufzeit
von isort ist Θ(n 2 ). Denkaufgabe: Gibt es eine Funktion f, so daß die Aussage „Die
asymptotische Laufzeit von isort ist Θ(f)“ korrekt ist?
Die asymptotische Betrachtungsweise hat viele Vorteile: Sie setzt nachträglich unsere
zu Beginn dieses Kapitels getroffenen Abstraktionen ins Recht. Wenn wir die asymptoti-
sche Laufzeit von Funktionen analysieren, ist es in der Tat korrekt, die Anwendung einer
Gleichung als einen Schritt zu zählen. Warum? Nun, die Gestalt der Gleichungen hängt
nicht von der Eingabe ab, ist also konstant. Jede Gleichung faßt eine feste Anzahl (einfacherer)
Rechenschritte zusammen; das Ergebnis der Analyse kann somit nur um einen
konstanten Faktor verfälscht werden. Die Konstante fällt aber in der Θ-Notation wieder
unter den Tisch. Gleiches gilt für den Einfluß des Compilers: Sofern jede Haskell- Rechenregel
auf eine feste Anzahl von Maschineninstruktionen abgebildet wird, kommt es für die
asymptotische Effizienz aufs Gleiche heraus, ob wir Maschineninstruktionen oder Haskell-
Regeln als Einheit wählen. Und schließlich macht auch die unterschiedliche Taktrate der
Rechner Warp III und Slack I nur einen konstanten Faktor aus, für die asymptotische
Effizienz also keinen Unterschied.
Wir dürfen sogar noch konsequenter sein und nur „laufzeitbestimmende“ Operationen
zählen: Getreu der asymptotischen Betrachtungsweise können wir eine Operation X als
Lisa Lista: Harry, damit sind unsere früheren Bedenken gegen
die Einheit Rechenschritt ausgeräumt, oder?
Harry Hacker: Sind sie — bis auf einen letzten Punkt. Vielleicht
sollte ich mal den Source-Code des Haskell-Compilers durchlesen.

Prof. Paneau: Wobei nicht verschwiegen werden sollte, daß
sich bei der Bestimmung der bestimmenden Operation schon
mancher verschätzt hat. Strenggenommen muß für jede Regel
nachgewiesen werden, daß für sie T Y CT X gilt, und zwar für
ein festes C. Die Informatiker gehen damit oft sehr intuitiv um.
Übung 5.2 Nimm an, daß das Einfügen eines Elementes in eine
Liste durch insert im Durchschnitt in der Mitte der Liste erfolgt.
Leite unter dieser Annahme die average-case Effizienz von
isort ab. Wo liegt der Unterschied zum worst case?
92 5. Effizienz und Komplexität
bestimmend ansehen, wenn für jede andere Operationen Y gilt T Y ∈ O(T X). Die Sortierfunktionen
basieren z.B. auf dem Vergleich von Elementen; die Anzahl der durchgeführten
Vergleichsoperationen bestimmt somit im wesentlichen die Laufzeit der Funktionen. Im
nächsten Abschnitt werden wir sehen, daß die Analyse von isort die gleiche asymptoti-
sche Laufzeit ermittelt, wenn wir nur die Vergleichsoperationen zählen.
Die Vorteile der asymptotischen Betrachtungsweise sind auch ihre Nachteile: Ist die
verborgene Konstante sehr groß, kann ein Verfahren trotz guter asymptotischer Laufzeit
in der Praxis unbrauchbar sein. Auf die Algorithmen, die wir betrachten, trifft das Gott sei
Dank nicht zu.
Noch eine letzte Bemerkung zur Art der Analyse. Bisher haben wir den „best case“ und
den „worst case“ untersucht. Man kann auch den Resourcenverbrauch für den „average
case“ berechnen. Die Analyse des durchschnittlichen Falls ist aber im allgemeinen sehr
schwierig: Sie setzt voraus, daß man Kenntnis über die Häufigkeitsverteilung der Eingaben
hat. Selbst wenn man — ob nun gerechtfertigt oder nicht — annimmt, daß alle Eingaben
gleich wahrscheinlich sind, bleibt die Analyse aufwendig.
5.2. Effizienz strukturell rekursiver Funktionen
Bestimmen wir noch einmal die „worst case“-Laufzeit von isort, indem wir nur die Anzahl
der benötigten Vergleichsoperationen bestimmen. Das vereinfacht das Zählen und
auch die Rekurrenzgleichungen.
T insert(0) = 0
T insert(n + 1) = 1 + T insert(n)
T isort(0) = 0
T isort(n + 1) = T insert(n) + T isort(n)
Die Gleichungen haben eine besonders einfache Form, die gut als Summenformel geschrieben
werden kann. Man rechnet schnell nach, daß eine Kostenfunktion der Form
die geschlossene Form
C(0) = c
C(n + 1) = f(n + 1) + kC(n)
C(n) = k n c +
nX
k n−i f(i) (5.10)
hat. Im Fall von T insert und T isort ist die Konstante k gleich 1, da die Funktionen wie
auch der Datentyp Liste linear rekursiv sind: In der definierenden Gleichung kommt das
i=1

5.2. Effizienz strukturell rekursiver Funktionen 93
definierte Objekt genau einmal auf der rechten Seite vor. Mithilfe der Summenformel lassen
sich die Kostenfunktionen für insert und isort leicht in eine geschlossene Form
bringen.
T insert(n) =
T isort(n) =
nX
1 = n ∈ Θ(n)
i=1
nX
i=1
i − 1 = 1
2 n(n − 1) ∈ Θ(n2 )
Wir sehen: Wenn wir durch die asymptotische Brille blicken, erhalten wir das gleiche
Ergebnis wie in Abschnitt 5.1.2.
Bisher haben wir den Zeitbedarf von isort analysiert. Widmen wir uns jetzt dem Platzbedarf.
Bei der Analyse kommen uns die Überlegungen zur asymptotischen Komplexität
ebenfalls zu Gute: Auch hier spielen konstante Faktoren keine Rolle. Schauen wir uns den
typischen Verlauf einer Rechnung an.
isort [a1, ..., an−1, an]
⇒ insert a1 (· · · (insert an−1 (insert an [])) · · ·)
⇒ [aπ(1), ..., aπ(n−1), aπ(n)]
In der Mitte der Rechnung harren n Anwendungen von insert ihrer Abarbeitung. Während
der Abarbeitung von insert ai x vergrößert sich die Formel kurzfristig etwas; am
Ende steht die um ai erweiterte Liste x. Summa summarum ist der Platzbedarf proportional
zur Länge der Eingabeliste.
Space(insert a x) ∈ Θ(length x)
Space(isort x) ∈ Θ(length x)
Strukturell rekursive Funktionen auf Listen sind in der Regel gut zu analysieren, da die
resultierenden Rekurrenzgleichungen eine einfache Form haben. Funktionen auf Bäumen
stellen uns vor größere Probleme; dafür ist der Erkenntnisgewinn auch größer. Die Funktion
sortTree, die einen Baum in eine sortierte Liste überführt, illustriert dies eindrucksvoll.
sortTree :: Tree Integer -> [Integer]
sortTree (Leaf a) = [a]
sortTree (Br l r) = merge (sortTree l) (sortTree r)
[In den nachfolgenden Rechnungen kürzen wir sortTree mit sT ab.] Wir wollen die
„worst case“-Laufzeit von sortTree bestimmen; wie bereits praktiziert zählen wir zu
diesem Zweck nur die Vergleichsoperationen. Das Verhalten von merge ist schnell geklärt:
T merge(m, n) = m + n − 1 für m, n 1

Übung 5.3 Zeige, daß 1
n(n − 1) die obige Rekurrenzgleichung
2
tatsächlich erfüllt.
Übung 5.4 Beweise die Eigenschaft 2ˆ(depth t - 1) <
size t 2ˆdepth t .
94 5. Effizienz und Komplexität
Der schlechteste Fall für merge liegt vor, wenn beide Listen wie ein Reißverschluß verzahnt
werden müssen: merge [0,2..98] [1,3..99]. [Ideal wäre es, wenn alle Elemente
der kürzeren Liste kleiner sind als die der längeren Liste.]
Die Größe der Eingabe entspricht bei listenverarbeitenden Funktionen der Länge der
Liste. Was ist die bestimmende Eingabegröße im Fall von sortTree? Zur Listenlänge
korrespondiert die Anzahl der Blätter eines Baums — zu length korrespondiert size.
Versuchen wir unser Glück:
T sT(1) = 0
T sT(n) = n − 1 + max{ T sT(i) + T sT(n − i) | 0 < i < n }
Da wir nur die Größe des Baums kennen, nicht aber die Verteilung der Blätter auf den
linken und rechten Teilbaum, sind wir gezwungen alle möglichen Kombinationen durchzuprobieren.
Schließlich wollen wir ja die „worst case“-Laufzeit bestimmen. Es ist immer
hilfreich, unbekannte Funktionen für kleine Werte zu tabellieren:
Man sieht, wir erhalten:
n 1 2 3 4 5 6 7 8 9
T sT(n) 0 1 3 6 10 15 21 28 36
T sT(n) =
nX
i=1
i − 1 = 1
2 n(n − 1) ∈ Θ(n2 )
Der schlechteste Fall tritt somit ein, wenn der linke Teilbaum nur einen Knoten enthält
und der rechte alle übrigen, oder umgekehrt. Dann gilt gerade: size t = depth t + 1.
Die Verwendung von size als Maß für die Größe eines Baums ist eigentlich nicht
besonders motiviert, genausogut könnten wir die Tiefe eines Baumes heranziehen. Los
geht’s:
T ′
sT(0) = 0
T ′
sT(n + 1) = 2 n+1 − 1 + 2T ′
sT(n)
Die Kosten für den Aufruf von merge, sprich die Anzahl der Knoten im Baum, haben wir
mit Gleichung (4.13) grob nach oben abgeschätzt. Die Rekurrenzgleichungen können wir
mit (5.10) lösen:
T ′
sT(n) =
nX
2 n−i (2 i − 1) =
i=1
nX
2 n − 2 n−i = n2 n − 2 n + 1 ∈ Θ(n2 n )
i=1
Hier ist der schlechteste Fall kurioserweise der ausgeglichene Baum 2 , dessen Größe durch
2ˆ(depth t - 1) < size t 2ˆdepth t eingeschränkt ist. Jetzt betrachten wir
2 Zur Erinnerung: Ein Baum heißt ausgeglichen, wenn sich die Größe der Teilbäume für jede Verzweigung um
maximal eins unterscheidet.

5.2. Effizienz strukturell rekursiver Funktionen 95
beide Ergebnisse noch einmal und gleichen die Resultate mit den jeweiligen Beziehungen
zwischen Größe und Tiefe der Bäume ab. In beiden Fällen erhalten wir depth t*size t
als „worst case“-Laufzeit. Die Laufzeit wird durch das Produkt von Größe und Tiefe bestimmt:
T ime(sortTree t) depth t*size t
Wir sehen: Die Laufzeit von sortTree läßt sich am genauesten bestimmen, wenn wir
sowohl die Größe als auch die Tiefe des Baums berücksichtigen.
T ′′
sT(s, d) = sd
Für unsere Mühen werden wir freilich auch belohnt: Mit der Analyse von sortTree
haben wir so nebenbei auch isort und mergeSort erledigt! Die Aufrufstruktur von
isort entspricht gerade einem rechtsentarteten Baum. Aus size t = depth t+1 folgt
das bereits bekannte Resultat:
T isort(n) = T ′′
sT(n, n − 1) ∈ Θ(n 2 )
Der von mergeSort abgearbeitete Baum ist hingegen ausgeglichen. Wir wissen ja bereits,
daß build stets ausgeglichene Bäume erzeugt. Aus 2ˆ(depth t - 1) < size t
2ˆdepth t folgt dann
und
T mergeSort(n) = T sortTree(n) + T build(n)
n⌊log 2 n⌋ T ′′
sT (n, ⌊log 2 n⌋) T mergeSort(n) T ′′
sT (n, ⌈log 2 n⌉) n⌈log 2 n⌉
Da build überhaupt keine Vergleiche durchführt, gilt
T build = 0
und somit (das Weglassen der Basis des Logarithmus ist durch 5.7 gerechtfertigt)
T mergeSort (n) ∈ Θ(n log n).
Aus den Ergebnissen läßt sich unmittelbar folgern, daß Sortieren durch Fusionieren eine
asymptotisch bessere „worst case“-Laufzeit als Sortieren durch Einfügen hat.
Der Platzbedarf von mergeSort ist genau wie der von insertionSort linear in der
Länge der Eingabeliste. Dazu überlegt man sich, wieviele Knoten der Aufrufbaum von
mergeSort enthält.
mergeSort [a1, ..., an−1, an]
⇒ merge (· · ·(merge [a1] [a2])· · ·) (· · ·(merge [an−1] [an])· · ·)
⇒ [aπ(1), ..., aπ(n−1), aπ(n)]
Übung 5.5 Zeige durch strukturelle Induktion über t, daß die
Beziehung T ime(sortTree t) depth t*size t gilt.

96 5. Effizienz und Komplexität
In der Mitte der Rechnung harren n − 1 merge-Aufrufe ihrer Abarbeitung. Somit ist die
maximale Größe der Formel proportional zur Größe der Eingabeliste.
Space(mergeSort x) ∈ Θ(length x)
Jetzt haben wir alle Informationen zusammen, um die beiden Sortierverfahren quantitativ
miteinander zu vergleichen. Da der Platzbedarf asymptotisch gleich ist, betrachten
wir nur den Bedarf an Rechenzeit. Klar, die Funktion n log n ist kleiner als n 2 , also ist
mergeSort effizienter als insertionSort. Aber, um wieviel effizienter? Ein paar Zahlen
verdeutlichen den Unterschied:
n n log 2 n n 2
10 3 ≈ 10, 0 ∗ 10 3 10 6
10 4 ≈ 13, 3 ∗ 10 4 10 8
10 5 ≈ 16, 6 ∗ 10 5 10 10
10 6 ≈ 19, 9 ∗ 10 6 10 12
Ist n gleich Tausend, ist Sortieren durch Fusionieren 100-mal schneller als Sortieren durch
Einfügen; für n gleich eine Million beträgt der Faktor schon 50.000. Je größer die Listen
werden, desto größer ist der Geschwindigkeitsgewinn.
Harry Hacker und Lisa Lista erhalten den Auftrag einen, Datensatz mit 1.000.000 Einträgen nach
bestimmten Kriterien zu sortieren. Harry verläßt sich auf sein Equipment, Warp III mit dem Übersetzer
Turbo-Haskell, und implementiert zu diesem Zweck Sortieren durch Einfügen. Durch geschickte
Programmierung und aufgrund der Verwendung eines optimierenden Übersetzers, benötigt das resultierende
Programm 2n 2 Rechenschritte, um eine n-elementige Liste zu sortieren. Lisa Lista hat
sich vorher in die Literatur vertieft und Sortieren durch Fusionieren gefunden. Ihre Implementierung
ist nicht besonders ausgefeilt und da sie einen schlechten Übersetzer verwendet, benötigt ihr Programm
80n log 2 n Rechenschritte. Harrys Warp III schafft durchschnittlich 750.000 Rechenschritte
pro Sekunde, Lisas Slack I nur 50.000. Trotzdem wartet Harry — falls er so viel Geduld hat — rund
einen Monat auf das Ergebnis
2 · (10 6 ) 2
750.000
≈ 2.666.666 Sekunden ≈ 30, 9 Tage,
während Lisa nach rund neun Stunden den sortierten Datensatz vorliegen hat:
80 · (10 6 ) · log 2 (10 6 )
50.000
≈ 31.891 Sekunden ≈ 8, 9 Stunden.
In einigen Fällen schneidet insertionSort allerdings besser ab als mergeSort: Gerade
dann, wenn die Liste im wesentlichen schon sortiert ist. Dann benötigt insertionSort
statt quadratischer nur noch lineare Laufzeit, während sich an dem Verhalten von mergeSort

5.3. Effizienz wohlfundiert rekursiver Funktionen 97
asympotisch nichts ändert. Nur der konstante Faktor wird etwas besser. Nachrechnen!
Ob der Fall der (fast) vorsortierten Liste häufig auftritt, hängt von der jeweiligen Anwendung
ab. Manchmal ist es sinnvoll, ihn zu berücksichtigen. Wir kommen darauf in
Abschnitt 5.5.2 zurück.
5.3. Effizienz wohlfundiert rekursiver Funktionen
Einige der bisher definierten Funktionen basieren auf dem Prinzip der wohlfundierten Rekursion:
power, leaves und build. Die Funktion power analysieren wir in Abschnitt 5.8,
build und leaves kommen hier an die Reihe. Beginnen wir mit build. Wir gehen hier
etwas genauer vor und zählen alle Rechenschritte, weil wir später (Abschnitt 5.5) auch für
die konstanten Faktoren interessieren werden. Auch die Konstruktoranwendungen zählen
mit, schließlich besteht der Zweck von build gerade im Baumaufbau. Wir gehen von der
ursprünglichen Definition von build aus:
build [] = Nil
build [a] = Leaf a
build (a:as) = Br (build (take k as))(build (drop (n-k) as))
where k = length as ‘div‘ 2
Die Effizienz von take und drop haben wir bereits analysiert; build verwendet außerdem
length, was besonders einfach zu analysieren ist:
T build(0) = 1
T build(1) = 1
T take(k, n) = T drop(k, n) = min(k, n)
T length(n) = T length (n) = n + 1 ∈ Θ(n).
T build(n) = 1 + T length(n) + T take(k, n) + T drop(k, n) + T build(⌊n/2⌋) + T build(⌈n/2⌉) für n > 1
= 1 + (n + 1) + 2(⌊n/2⌋ + 1) + T build(⌊n/2⌋) + T build(⌈n/2⌉)
Zur Vereinfachung nehmen wir an, daß die Division durch 2 immer aufgeht, also n = 2 m
gilt. Wir erhalten damit
T build(2 m ) = 1
T build(2 m ) = 2 ∗ 2 m + 4 + 2T build(2 m−1 )
= (m + 2)2 m+1 + 2 m − 4

Prof. Paneau: Natürlich erwarte ich von einer gewissenhaften
Studentin, daß sie die Summenformel aufstellt und die geschlossene
Form von T build nachrechnet.
Grit Garbo: Ehrenwert, Herr Kollege, aber mühsam. Ich würde
den Ansatz T build(2 m ) = (m + x)2 m+1 − y aufstellen und die
Parameter x und y aus den beiden Rekursionsgleichungen bestimmen.
Harry Hacker: Und wenn wir T build ∈ Θ(n 2 ) berechnet hätten?
Lisa Lista: Dann wäre auch T mergeSort ∈ Θ(n 2 ), und unsere frühere
Analyse allein auf Basis der Zahl der Vergleiche wäre falsch
gewesen.
Prof. Paneau: Genau, liebe Studenten. Bei der Bestimmung der
bestimmenden Operation hat sich schon mancher vergriffen.
Auch das Vereinfachen will eben gelernt sein.
98 5. Effizienz und Komplexität
Ersetzen wir 2 m wieder durch n, so ergibt sich
T build(0) = 1
T build(n) = 1
T build(n) = 2n(log n + 2) + n − 4 ∈ Θ(n log n)
Da wir den Fall, daß die Division durch 2 nicht aufgeht, durch einen konstanten Faktor
abschätzen können, gilt die asymptotische Aussage für beliebige Werte von n. Damit
fällt build in die gleiche Effizienzklasse wie sortTree, und unsere Aussage T mergeTree ∈
Θ(n log n) ist endgültig gerechtfertigt.
Wenden wir uns der wohlfundiert rekursiven Funktion leaves zu, die die Blätter eines
Baums ermittelt. Wie im Fall von sortTree haben wir das Problem, wie wir die bestimmende
Eingabegröße von leaves wählen: Sowohl size als auch depth scheitern, da die
dritte Gleichung von leaves zu der paradoxen Rekurrenzgleichung
T leaves(n) = 1 + T leaves(n)
führt. Beide Maße auf Bäumen scheitern, da sie die algorithmische Idee von leaves
nicht berücksichtigen. Was tun? Nun, eigentlich haben wir das Problem schon gelöst:
Der Induktionsbeweis in Abschnitt 4.6 verwendet ein Maß auf Bäumen, weight, dessen
Wert für jeden rekursiven Aufruf gerade um eins abnimmt. Also erhalten wir ohne weitere
Überlegungen:
T ime(leaves t) = weight t + 1
Wir müssen noch eins addieren für den Fall, daß t ein Blatt ist. Aus size t weight t <
2*size t folgt:
T leaves(n) ∈ Θ(n)
Wir sehen: Unsere damaligen Anstrengungen werden belohnt. Die Relation „≺“ bzw. die
Funktion weight klären nicht nur, warum leaves terminiert, sondern auch wie schnell.
5.4. Problemkomplexität
Wir haben bisher zwei Sortierverfahren kennengelernt: isort mit einer „worst case“-
Laufzeit von Θ(n 2 ) und mergeSort mit einer „worst case“-Laufzeit von Θ(n log n). Es
stellt sich die Frage, ob mit Sortieren durch Fusionieren bereits das Ende der Fahnenstange
erreicht ist, oder ob man andere Verfahren mit einer noch besseren asymptotischen
Laufzeit entwickeln kann. In diesem Abschnitt beschäftigen wir uns mit der Komplexität
des Sortierproblems: Wie schnell kann man durch Vergleich von Elementen sortieren?
Man sollte sich zunächst klarmachen, daß diese Fragestellung von einer anderen Qualität

5.4. Problemkomplexität 99
ist als die in den letzten Abschnitten behandelte: Wir analysieren nicht die Effizienz eines
Sortierverfahrens, sondern die Komplexität des Sortierproblems. Dabei ist die (asymptotische)
Komplexität eines Problems bestimmt als die (asymptotische) Effizienz des besten
Programms, das dieses Problem löst.
Vorher halten wir noch einen Moment inne, denn es ist keine Selbstverständlichkeit,
daß dies überhaupt eine vernünftige Frage ist. Es ist zwar eine verbreitete Redensart, von
der Komplexität von Problemen aller Art zu sprechen. Nun macht man als Wissenschaftler
täglich die Erfahrung, daß zwar manche Dinge zunächst kompliziert erscheinen, aber
immer einfacher werden, je besser man gedanklich erfaßt hat. Wenn also jemand von der
Komplexität eines Problems spricht, so ist es — im einfachsten Fall — eine Aussage über
sein eigenes, mangelhaftes Verständnis. Mag sein, daß auch einer angeben möchte mit
der Komplexität der Dinge, mit denen er sich beschäftigt. Oder er will gar andere davon
abhalten, hier allzusehr auf Klärung zu bestehen ... Was immer es auch sei, eines gibt es
nicht: Eine am Problem selbst festzumachende, objektivierbare Komplexität.
In der Algorithmik allerdings gibt es sie tatsächlich. Das liegt einfach daran, daß wir beim
algorithmischen Problemlösen uns auf einen festen Satz von Rechenregeln festlegen — auf
den Befehlssatz unseres Rechners, oder die Rechenregeln unserer Sprache Haskell. Darauf
bezogen kann man nachweisen, daß es untere Schranken für die Effizienz der Lösung
eines Problems gibt, die sich auf der Basis dieser Rechenregeln nicht unterbieten lassen.
Deshalb ist es korrekt, hier von der Problemkomplexität zu sprechen, ohne damit dem
sonst so fragwürdigen Gebrauch des Begriffes Komplexität recht zu geben.
Fangen wir klein an und überlegen, wieviele Vergleichsoperationen man mindestens
benötigt, um eine 2- oder 3-elementige Liste zu sortieren. Die Sortierprogramme lassen
sich gut durch Entscheidungsbäume darstellen: Die Verzweigungen sind mit Vergleichsoperationen
markiert, die Blätter mit den Permutationen der zu sortierenden Liste. Zwei
Entscheidungsbäume sind nachfolgend abgebildet.
a1

100 5. Effizienz und Komplexität
Anzahl der Permutationen einer n-elementigen Liste n!. Mit (4.15) können wir die Anzahl
der benötigten Vergleichsoperationen nach unten abschätzen:
T imesort(n) log 2(n!)
Die Fakultätsfunktion läßt sich mit der Stirlingschen Formel abschätzen:
Insgesamt erhalten wir
T imesort(n) log 2
n! √ 2πn
√ 2πn
n
n .
e
n
n ∈ Θ(n log n)
e
Daraus ergibt sich, daß Ω(n log n) eine untere Schranke für das Sortieren durch Vergleichen
ist. Da Mergesort eine „worst case“-Laufzeit von Θ(n log n) hat, wird die Schranke auch
erreicht. Verfahren, deren „worst case“-Laufzeit mit der unteren Schranke der für das
Problem ermittelten Komplexität zusammenfällt, nennt man auch asymptotisch optimal.
Asymptotisch optimale Sortierverfahren sind Mergesort und Heapsort. Nicht optimal sind
Sortieren durch Einfügen, Minimumsortieren, Bubblesort und Quicksort.
Wir betonen noch einmal, daß Ω(n log n) eine untere Schranke für das Sortieren durch
Vergleichen ist. Wenn wir zusätzliche Annahmen über die zu sortierenden Elemente machen
können, läßt sich das Sortierproblem unter Umständen schneller lösen. Wissen wir
z.B., daß alle Elemente in dem Intervall [l . . . r] liegen, wobei r −l nicht sehr groß ist, dann
können wir auch in Θ(n) sortieren, siehe Abschnitt 5.6.
Im Idealfall sieht der Weg zu einer guten Problemlösung so aus:
1. Man verschafft sich Klarheit über die Komplexität des zu lösenden Problems.
2. Man entwickelt einen Algorithmus, dessen Effizienz in der Klasse der Problemkomplexität
liegt. Asymptotisch gesehen, ist dieser bereits „optimal“.
3. Man analysiert die konstanten Faktoren des Algorithmus und sucht diese zu verbessern.
An den konstanten Faktoren eines Algorithmus zu arbeiten, der nicht der asymptotisch
optimalen Effizienzklasse angehört, macht in der Regel keinen Sinn, weil das aymptotische
bessere Verhalten letztlich (also für große n) immer überwiegt. Allerdings darf man
sich auf diese Regel nicht blind verlassen und muß sich fragen, wie groß die Eingabe praktisch
werden kann. Hat man z.B. ein Problem der Komplexität Θ(n) und ein asymptotisch
optimales Programm p1 mit großem konstantem Faktor C, so ist eventuell ein asymptotisch
suboptimales Programm p2 mit T imep2(n) ∈ Θ(n log n) vorzuziehen, wenn es einen

5.5. Anwendung: Optimierung von Programmen am Beispiel mergeSort 101
kleinen konstanten Faktor c hat. Ist zum Beispiel C = 10 und c = 1, so ist Programm p2
bis hin zu n = 10 10 schneller. In den meisten Anwendungen würde dies den Ausschlag für
p2 geben.
Die Problemkomplexität Θ(f) heißt polynomial, wenn f ein Polynom in n ist, und exponentiell,
wenn n im Exponenten auftritt. Probleme exponentieller Komplexität nennt man
gerne „nicht praktikabel“ (untractable), um anzudeuten, daß bereits für sehr kleine Eingaben
der Aufwand nicht mehr mit den verfügbaren Zeit-und Platzresourcen zu bewältigen
ist. Probleme mit polynomialer Effizienz gelten als „praktikabel“ (tractable), allerdings darf
der Grad des Polynoms nicht allzu hoch sein.
Hierzu einige Beispiele aus der molekularen Genetik:
• Das Problem, eine kurze DNA-Sequenz in einer längeren zu finden, liegt in Θ(n). Ist
die lange Sequenz z.B. ein komplettes bakterielles Genom, so liegt n etwa bei 3∗10 6 .
• Der Ähnlichkeitsvergleich zweier DNA-Sequenzen besteht darin, daß man beide
durch Enfügen von Lücken so untereinander arrangiert, daß möglichst viele gleiche
Nukleotide untereinander stehen. Der Vergleich zweier Sequenzen der Länge
n hat die Komplexität Θ(n 2 ). Hier ist n praktisch auf wenige tausend Nukleotide
beschränkt.
• Die zweidimensionale Faltungsstruktur einer RNA (das ist eine einsträngige Variante
der DNA) läßt sich mit einem thermodynamischen Modell berechnen. Die Effizienz
des Verfahrens liegt bei Θ(n 3 ) mit einem großen konstanten Faktor, so daß Strukturen
von RNA-Molekülen nur bis zu einer Länge von ca. 500 Nukleotiden berechnet
werden können.
• Der simultane Vergleich von k DNA-Sequenzen der Länge n ist eine zentrale Frage
der Molekularbiologie, weil er Rückschlüsse auf evolutionäre Verwandschaft und
gemeinsame Funktionen gibt. Er hat die Effizienz Θ(2 k−1 n k ) und kann daher nur für
wenige oder sehr kurze Sequenzen durchgeführt werden.
Allerdings finden Informatiker auch im Falle von nicht praktikablen Problemen in der
Regel einen Ausweg. Dieser kann zum Beispiel darin bestehen, daß das Problem nicht
exakt, sondern nur näherungsweise (aber effizienter) gelöst wird. Hier eröffnet sich ein
weites Feld der Algorithmik, das wir aber nicht betreten wollen.
5.5. Anwendung: Optimierung von Programmen am
Beispiel mergeSort
Optimierung von Programmen hat wenig mit Optimalität zu tun — es ist nur ein schlechter,
aber üblicher Ausdruck für die Verbesserung der Effizienz. Sinnvolle Optimierung setzt

102 5. Effizienz und Komplexität
voraus, daß man sich im klaren ist über die „Schwächen“ des vorliegenden Programms und
die Chancen, seine Effizienz zu verbessern. Im diesem Abschnitt geht es um die Verbesserung
der konstanten Faktoren.
Wir haben in Abschnitt 5.4 gesehen, daß Mergesort ein asymptotisch optimales Verfahren
ist. Trotzdem kann man noch viel verbessern; die Tatsache, daß Mergesort asymptotisch
optimal ist, sagt uns, daß es auch sinnvoll ist, bei Mergesort anzusetzen. Wir
werden zwei Verbesserungen vorführen, eine offensichtliche und eine vielleicht weniger
offensichtliche. Die offensichtliche Verbesserung besteht darin, aus einer Vor- oder Teilsortierung
der Liste Nutzen zu ziehen. Dies zu tun ist naheliegend und auch angebracht,
denn die Laufzeit von mergeSort ist weitestgehend unabhängig von der Anordnung der
Elemente in der Liste: Auch die „best case“-Laufzeit ist Θ(n log n). Hier schneidet isort
mit einer „best case“-Laufzeit von Θ(n) besser ab (scheitert allerdings, wenn die Liste
absteigend sortiert ist). Die weniger offensichtliche Verbesserung zielt darauf ab, die unproduktive
Teile-Phase zu optimieren. Fangen wir mit der weniger offensichtlichen Verbesserung
an.
5.5.1. Varianten der Teile-Phase
Wir nehmen nun die Effizienz der Funktion build näher unter die Lupe.
Wie können wir den build-Schritt verbessern? Die wiederholte Längenbestimmung
der Teillisten ist überflüssig, wenn man die Länge als zusätzliches Argument mitführt:
build’’ :: [a] -> Tree a
build’’ as = buildn (length as) as
where buildn :: Int -> [a] -> Tree a
buildn 1 (a:as) = Leaf a
buildn n as = Br (buildn k (take k as))
(buildn k (drop k as))
where k = n ‘div‘ 2
Was genau ändert sich dadurch? Vergleichen wir buildn mit build, das wir in Abschnitt
5.3 analysiert haben. Dort ist anstelle von T length(n) nun T div + T − einzusetzen,
der Beitrag n + 1 reduziert sich zu 2. Damit gilt: Die Funktion buildn löst also das Problem
ebenfalls in einer Laufzeit von Θ(n log n). Der konstante Faktor halbiert sich jedoch
gegenüber build.
Ein schöner Fortschritt, könnte man meinen. Allerdings — da war ja noch die mittels
buildSplit definierte Funktion build’ aus Abschnitt 3.4 . Die Analyse der Effizienz
hatten wir auf später vertagt — hier ist sie.
buildSplit verwendet weder length noch take. Die entscheidende Gleichung ist
buildSplit n as = (Br l r, as’’)

5.5. Anwendung: Optimierung von Programmen am Beispiel mergeSort 103
where k = n ‘div‘ 2
(l,as’) = buildSplit k as
(r,as’’) = buildSplit (n-k) as’
Für Arithmetik und Konstruktoren fallen 6 Rechenschritte an, und wir erhalten
T buildSplit(n) = 6 + T buildSplit (⌊n/2⌋) + T buildSplit (⌈n/2⌉)
T buildSplit(1) = 1
Als Lösung dieses Gleichungssystems ergibt sich für n = 2 k genau T buildSplit(2 k ) =
6(2 k+1 − 1) = 12n − 6 ∈ Θ(n). Damit liegt build’ sogar in einer besseren Effizienzklasse
als build’’, allerdings mit einem etwa zehnfach schlechteren konstanten Faktor. Erst ab
log n = 12, also n = 2 12 wird die asymptotisch bessere Funktion build’ auch praktisch
besser sein.
Aber kann man den Baumaufbau nicht ganz weglassen, wenn man die aufgespaltenen
Listen gleich fusioniert? Wir eliminieren damit die Datenstrukur, die die beiden Phasen
trennt. Das funkioniert ganz systematisch: Wir rechnen einige Schritte mit den definierenden
Gleichungen von mergeSort. Ausgangspunkt ist die Gleichung
mergeSort as = sortTree (build as)
Wir setzen für as die Fälle [], [a] und (a:as) ein und leiten neue Gleichungen ab:
mergeSort [] = sortTree(build []) = sortTree Nil = []
mergeSort [a] = sortTree(build [a]) = sortTree (Leaf a) = [a]
mergeSort (a:as) = sortTree(build (a:as))
= sortTree(Br (build (take k as)) (build (drop k as)))
where k = length as ‘div‘ 2
= merge (sortTree (build (take k as))
sortTree (build (drop k as)))
where k = length as ‘div‘ 2
= merge (mergeSort (take k as)
mergeSort (drop k as)))
where k = length as ‘div‘ 2
Im letzten Schritt haben wir die definierende Gleichung von mergeSort gleich zweimal
angewandt (und zwar von rechts nach links), um die Funktionen sortTree und build
endgültig zum Verschwinden zu bringen. Als Fazit erhalten wir eine „baumfreie“ Variante
von mergeSort:
mergeSort’ [] = []
mergeSort’ [a] = [a]
mergeSort’ (a:as) = merge (mergeSort (take k as))
(mergeSort (drop k as))
where k = length as ‘div‘ 2
Übung 5.6 Analysiere die Effizienz von mergeSort anhand der
hier abgeleiteten Definition.

104 5. Effizienz und Komplexität
Was haben wir erreicht? Die Datenstruktur des Baumes ist nur scheinbar verschwunden
— sie tritt nun als Aufrufufstruktur von mergeSort’ auf: Wo bisher eine Verzweigung
Br l r zwei Teilaufgaben zusammenhielt, ist es nun ein Aufruf der Form merge xs ys,
der nicht ausgerechnet werden kann ehe die Teilprobleme xs und ys gelöst sind. An der
aymptotischen Effizienz hat sich nichts geändert, und einen dramatischen Vorteil bei den
konstanten Faktoren dürfen wir auch nicht erwarten: Das Anwenden der Konstruktoren
Br, Nil und Leaf fällt weg, dafür hat merge ein Argument mehr als sortTree und
kostet vielleicht eine Kleinigkeit mehr. Wie diese Abwägung ausgeht, hängt eindeutig vom
Compiler ab und wird daher am einfachsten durch einen Test geklärt. Wir wählen eine
sortierte Liste, damit der Aufwand für merge minimal ausfällt, und andere Unterschiede
besser zu sehen sind:
mtest = mergeSort [1..10000]
mtest’ = mergeSort’ [1..10000]
Vom Standpunkt des systematischen Programmierens allerdings spricht alles für das ursprüngliche
mergeSort: Die Trennung in zwei Phasen führt zu einem sehr übersichtlichen
Programm, und noch dazu kann für die erste Phase die Funktion build wiederverwendet
werden. Das ist nicht nur bequem, sondern auch sicher. Entwickelt man mergeSort’ direkt,
muß man build implizit neu erfinden, und — Hand auf’s Herz — manch einer hätte
dabei vielleicht die Notwendigkeit der zweiten Gleichung übersehen und zunächst ein
fehlerhaftes Programm abgeliefert. Und last not least haben wir uns ja auch über die Effizienz
von build schon Gedanken gemacht, was zu der besseren Variante build geführt
hat. Auch diese Verbesserung müßte man bei mergeSort’ noch einmal programmieren.
Wir bleiben damit bei der Trennung in zwei Phasen und betrachten das Problem noch
einmal aus einem anderen Blickwinkel.
Alle Varianten von build konstruieren den Baum von oben nach unten (engl. top
down). Die Liste [a1,...,an] wir durch build in wenigen Schritten in den Baum Br
(build [a1,...,a ⌊n/2⌋]) (build [a ⌊n/2⌋+1,...,an]) überführt. Die oberste Verweigung
wird „zuerst“ erzeugt, die Teilbäume in weiteren Schritten. Da wir Bäume durch
Ausdrücke beschreiben, ergibt sich diese Vorgehensweise fast zwangläufig.
Aber eben nur fast; genausogut können wir einen Baum Ebene für Ebene von unten
nach oben aufbauen (engl. bottom up). Das funktioniert so: Nehmen wir an, wir hätten
schon Bäume der Tiefe k erzeugt:
/\ /\ /\ /\ /\ /\ /\
/t1\ /t2\ /t3\ /t4\ /t5\ /t6\ /t7\
---- ---- ---- ---- ---- ---- ----
Bäume der Tiefe k + 1 erhalten wir, indem wir zwei jeweils zwei benachbarte Bäume
zusammenfassen; eventuell bleibt ein Baum einer kleineren Tiefe als „Rest“.

5.5. Anwendung: Optimierung von Programmen am Beispiel mergeSort 105
o o o
/ \ / \ / \
/\ /\ /\ /\ /\ /\ /\
/t1\ /t2\ /t3\ /t4\ /t5\ /t6\ /t7\
---- ---- ---- ---- ---- ---- ----
Diesen Schritt wiederholen wir so oft, bis nur noch ein Baum verbleibt, also gerade ⌈log 2n⌉
mal. Um dieses Verfahren zu programmieren, muß man sich nur noch überlegen, daß man
die Zwischenergebnisse durch Listen von Bäumen repräsentiert. Im ersten Schritt ersetzen
wir jedes Listenelement a durch den Baum Leaf a.
bubuild :: [a] -> Tree a
bubuild = buildTree . map Leaf
Die Funktion buildLayer baut eine Ebene auf; buildTree iteriert buildLayer solange,
bis ein Baum übrigbleibt.
buildTree :: [Tree a] -> Tree a
buildTree [t] = t
buildTree ts = buildTree (buildLayer ts)
buildLayer :: [Tree a] -> [Tree a]
buildLayer [] = []
buildLayer [t] = [t]
buildLayer (t1:t2:ts) = Br t1 t2:buildLayer ts
Wie effizient ist buildTree? In jedem Schritt wird die Anzahl der Bäume halbiert,
wobei buildLayer n Konstruktoranwendungen für eine Liste mit n Bäumen benötigt.
T buildLayer (n) = n
T buildTree(1) = 0
T buildTree(n) = n + T buildTree (⌈n/2⌉) für n > 1
Lösen wir die Rekurrenzgleichung auf, erhalten wir T buildTree(n) ∈ Θ(n). Welches Ver-
fahren besser ist, buildn oder bubuild hängt letztlich noch vom verwendeten Übersetzer
ab; dazu lassen sich schlecht allgemeingültige Aussagen machen. Allerdings hat das
„bottom up“-Verfahren einen kleinen Nachteil: Es werden keine ausgeglichenen Bäume
erzeugt; der resultierende Baum ist am rechten Rand ausgefranst. Für n = 2 m + 1 erhalten
wir einen Baum, dessen linker Teilbaum ein vollständiger Binärbaum der Größe 2 m ist und
dessen rechter Baum die Größe 1 hat: In jedem Iterationsschritt bleibt der letzte Baum als
Rest.
Übung 5.7 Knobelaufgabe: Lisa Lista hat die folgende Variante
von buildTree entwickelt, die den letztgenannten Nachteil
mildern soll.
buildTree’ [t] = t
buildTree’ (t:ts) = buildTree’
(buildLayer (ts++[t]))
Ist das tatsächlich eine Verbesserung? Welche Eigenschaft haben
die resultierenden Bäume? Ist diese Variante im Hinblick auf die
Verwendung in mergeSort sinnvoll? Wie kann man den Aufruf
von (++) „wegoptimieren“?

106 5. Effizienz und Komplexität
5.5.2. Berücksichtigung von Läufen
Mergesort läßt sich relativ einfach so modifizieren, daß eine Vor- oder Teilsortierung der
Listen ausgenutzt wird. Eine auf- oder absteigend geordnete, zusammenhängende Teilliste
nennen wir Lauf (engl. run). Da für zwei aufeinanderfolgende Listenelemente stets ai
ai+1 oder ai ai+1 gilt, hat ein Lauf mindestens die Länge zwei. [Wenn wir von der
einelementigen Liste mal absehen.] Die Folge
enthält z.B. die folgenden fünf Läufe:
16 14 13 4 9 10 11 5 1 15 6 2 3 7 8 12
16 14 13 4 | 9 10 11 | 5 1 | 15 6 2 | 3 7 8 12.
Knobelaufgabe: Wieviele verschiedene Unterteilungen in 5 Läufe gibt es? Machen wir
uns daran, die Unterteilung einer Liste in eine Liste von Läufen zu programmieren. Wir
vergleichen zunächst die ersten beiden Elemente, um festzustellen, ob die Liste mit einem
auf- oder absteigendem Lauf beginnt. Für beide Fälle definieren wir eine Hilfsfunktion, die
den entsprechenden Lauf abtrennt.
runs :: [a] -> [[a]]
runs [] = [[]]
runs [a] = [[a]]
runs (a:b:x) = if a [a] -> [a] -> [[a]]
ascRun a as [] = [reverse (a:as)]
ascRun a as (b:y) = if a

5.6. Datenstrukturen mit konstantem Zugriff: Felder 107
Ein Sortierverfahren, das umso schneller sortiert je weniger Läufe die Liste enthält, heißt
geschmeidig (engl. smooth). Sortieren durch Fusionieren machen wir geschmeidig, indem
wir in der Teile-Phase Bäume konstruieren, die in den Blättern Läufe statt einzelne Elemente
enthalten.
smsort :: Ord a => [a] -> [a]
smsort = mergeRuns . build’ . runs
[Statt build’ können wir natürlich auch bubuild verwenden.] Die Herrsche-Phase
müssen wir leicht modifizieren:
mergeRuns :: Tree [a] -> [a]
mergeRuns (Leaf x) = x
mergeRuns (Br l r) = merge (mergeRuns l) (mergeRuns r)
Wir beschließen den Abschnitt mit einer kurzen Überlegung zur Effizienz von smsort.
Die Tiefe der konstruierten Binärbäume wird nicht mehr von der Anzahl der Elemente
bestimmt, sondern von der Anzahl der Läufe. An den Kosten pro Ebene ändert sich hingegen
nichts; diese sind weiterhin proportional zur Anzahl der Elemente. Ist l die Zahl der
Läufe, dann hat smsort eine Laufzeit von Θ(n log l).
5.6. Datenstrukturen mit konstantem Zugriff: Felder
Die Komplexität eines gegebenen Problems läßt sich nicht verbessern — es ist ja gerade
ihr Begriff, daß sie sich nicht unterbieten läßt. Allerdings ist es manchmal möglich, die
Problemstellung etwas einzuschränken, und dadurch in eine bessere Effizienzklasse zu
kommen. So haben wir bisher angenommen, daß wir beliebige Daten sortieren, die der
Typklasse Ord angehören. Wir wußten also nichts über die Daten außer daß uns eine
Vergleichsoperation Tree a. Wo wir bisher einen Tree a aufgebaut haben,
bauen wir nun mit der gleiche Funktion einen Tree [a]
auf.
Harry Hacker: Ist mir gar nicht aufgefallen!

108 5. Effizienz und Komplexität
[1 .. 99] Liste der positiven Zahlen bis einschließlich 99,
[1, 3 ..] Liste der ungeraden, positiven Zahlen,
[1, 3 .. 99] Liste der ungeraden, positiven Zahlen bis einschließlich 99.
Die Listen sind jeweils vom Typ [Integer]. Die untere und die obere Grenze können
durch beliebige Ausdrücke beschrieben werden. Die Schrittweite ergibt sich als Differenz
des ersten und zweiten Folgenglieds.
Um Funktionen auf Listen zu definieren, haben wir bis dato rekursive Gleichungen verwendet.
Manchmal können listenverarbeitende Funktionen einfacher und lesbarer mit
Listenbeschreibungen programmiert werden. Schauen wir uns ein paar Beispiele an: Die
Liste der ersten hundert Quadratzahlen erhält man mit
squares :: [Integer]
squares = [n*n | n [a]
divisors n = [d | d [a]
primes = [n | n

5.6. Datenstrukturen mit konstantem Zugriff: Felder 109
qsort’’ :: (Ord a) => [a] -> [a]
qsort’’ [] = []
qsort’’ (a:x) = qsort’’ [b | b

110 5. Effizienz und Komplexität
Element zugeordnet. Auch der Ausdruck array (l, u) vs, der ein Feld konstruiert,
enthält alle Zutaten einer Funktionsdefinition. Der Typ des Ausdrucks, Array a b, legt
den Vor- und Nachbereich fest, das Intervall (l, u) den Definitionsbereich; der Graph
der Funktion wird durch die Liste vs von Paaren beschrieben, wobei ein Paar (a, b) angibt,
daß dem Argument a der Wert b zugeordnet wird. Diese Zuordnung muß eindeutig
sein: Für (a, v) ‘elem‘ xs und (a, w) ‘elem‘ xs gilt stets v == w.
Felder sind sehr flexibel: Sowohl der Definitionsbereich als auch der Graph können
durch beliebige Ausdrücke beschrieben werden. Im obigen Beispiel ist der Graph durch
eine Listenbeschreibung gegeben. Felder sind effizient: Der Zugriff auf ein Feldelement,
der als Infixoperator (!) vordefiniert ist, erfolgt in konstanter Zeit.
squares’!7 ⇒ 17*17 ⇒ 49
Um den Zugriff in konstanter Zeit durchführen zu können, muß an den Indextyp allerdings
eine Anforderung gestellt werden: Das Intervall (l, u) muß stets endlich sein. Dies ist
gewährleistet, wenn l und u ganze Zahlen sind. Auch Tupel ganzer Zahlen sind erlaubt;
auf diese Weise können mehrdimensionale Felder realisiert werden. Das folgende Feld
enthält das kleine 1 × 1:
multTable :: Array (Int, Int) Int
multTable = array ((0,0),(9,9))
[((i,j),i*j) | i [a]
inRange :: (Ix a) => (a,a) -> a -> Bool
array :: (Ix a) => (a,a) -> [(a,b)] -> Array a b
bounds :: (Ix a) => Array a b -> (a,a)
assocs :: (Ix a) => Array a b -> [(a,b)]
(!) :: (Ix a) => Array a b -> a -> b
Mit range (l,u) erhält man die Liste aller Indizes, die in dem Intervall liegen; der
durch das Intervall beschriebene Bereich wird sozusagen als Liste aufgezählt. Die Funktion
inRange überprüft, ob ein Index in einem Intervall liegt. Ein Feld wird wie gesagt mit der
Funktion array konstruiert; mit bounds und assocs werden der Definitionsbereich und
der Graph eines Feldes ermittelt. Der Operator (!) entspricht der Funktionsanwendung.
Betrachtet man seinen Typ, so sieht man, daß der Indizierungsoperator ein Feld auf eine
Funktion abbildet.

5.6. Datenstrukturen mit konstantem Zugriff: Felder 111
Genug der Theorie, wenden wir uns weiteren Beispielen zu: Die Funktion tabulate
tabelliert eine Funktion in einem gegebenen Bereich.
tabulate :: (Ix a) => (a -> b) -> (a,a) -> Array a b
tabulate f bs = array bs [(i, f i) | i a*a) (0, 99). Eine Liste läßt sich leicht in ein Feld überführen.
listArray :: (Ix a) => (a,a) -> [b] -> Array a b
listArray bs vs = array bs (zip (range bs) vs)
Die vordefinierte Funktion zip überführt dabei zwei Listen in eine Liste von Paaren:
zip [a1,a2,...] [b1,b2,...] = [(a1,b1),(a2,b2),...]. Die Länge der kürzeren
Liste bestimmt die Länge der Ergebnisliste. Mit zip [0..] x werden die Elemente von
x z.B. durchnumeriert.
Ein Feld heißt geordnet, wenn i j ⇒ a!i a!j für alle Indizes i und j gilt. Stellen
wir uns die Aufgabe, ein Element in einem geordneten Feld zu suchen. Wenn wir das
Feld von links nach rechts durchsuchen, benötigen wir im schlechtesten Fall Θ(n) Schritte,
wobei n die Größe des Feldes ist. Sehr viel schneller ist das folgende Verfahren: Ist
(l,r) das Suchintervall, dann vergleichen wir das zu suchende Element mit dem mittleren
Feldelement a!m wobei m = (l + r) ‘div‘ 2 ist. Je nach Ausgang des Vergleichs
ist das neue Suchintervall (l, m-1) oder (m+1, r). In jedem Schritt wird die Größe des
Suchintervalls halbiert: Die asymptotische Laufzeit beträgt Θ(log n).
binarySearch :: (Ord b, Integral a, Ix a) => Array a b -> b -> Bool
binarySearch a e = within (bounds a)
where within (l,r) = l within (l, m-1)
EQ -> True
GT -> within (m+1, r)
Denkaufgabe: Warum heißt das Verfahren binäre Suche?
In der Liste von Argument-/Wertpaaren, die der Funktion array als zweites Argument
übergeben wird, darf jeder Index höchstens einmal auftreten. Die Funktion accumArray
erlaubt beliebige Listen; zusätzlich muß jedoch angegeben werden, wie Werte mit dem
gleichen Index kombiniert werden.
accumArray :: (Ix a) => (b -> c -> b) -> b ->
(a,a) -> [(a,c)] -> Array a b

112 5. Effizienz und Komplexität
Der Ausdruck accumArray (*) e bs vs ergibt das Feld a, wobei das Feldelement a!i
gleich (· · ·((e*c1)*c2)· · ·)*ck ist, wenn vs dem Index i nacheinander die Werte c1, . . . ,
ck zuordnet. Beachte: Ist die Operation (*) nicht kommutativ, spielt die Reihenfolge der
Elemente in vs eine Rolle.
5.7. Anwendung: Ein lineares Sortierverfahren
Wir illustrieren die Verwendung von accumArray mit zwei Sortierverfahren, die ganz anders
arbeiten, als die in Kapitel 4 vorgestellten. In beiden Fällen wird zusätzliches Wissen
über die zu sortierenden Elemente ausgenutzt. Gilt es, ganze Zahlen zu sortieren, von
denen wir wissen, daß sie in einem kleinen Intervall liegen, so zählen wir einfach die
Häufigkeit der einzelnen Elemente.
countingSort :: (Ix a) => (a, a) -> [a] -> [a]
countingSort bs x = [ a | (a,n) [[a]]
listSort bs xs
| drop 8 xs == [] = insertionSort xs
| otherwise = [[] | []

5.7. Anwendung: Ein lineares Sortierverfahren 113
(//) :: (Ix a) => Array a b -> [(a, b)] -> Array a b
Das Feld a//vs ist identisch mit a bis auf die in vs angegeben Stellen. Die folgende
Funktion, die eine Einheitsmatrix einer gegebenen Größe berechnet, demonstriert die
Verwendung von (//):
unitMatrix :: (Ix a, Num b) => (a,a) -> Array (a,a) b
unitMatrix bs@(l,r) = array bs’ [(ij,0) | ij LabTree b -> [(a,b)]
repr i Void = []
repr i (Node l a r) = [(i,a)] ++ repr (2*i) l ++ repr (2*i+1) r
treeArray :: (Num b, Ix b) => LabTree a -> Array b (Maybe a)
treeArray t = array bs [(i,Nothing) | i

114 5. Effizienz und Komplexität
Elements. Die freien Einträge enthalten in Wirklichkeit Nullen, aus Gründen der Übersichtlichkeit
sind sie nicht aufgeführt. Die Zahlen des Pascalschen Dreiecks erfüllen unzähligen
Eigenschaften, ein paar führen wir weiter unten auf. Zunächst kümmern wir uns darum,
ein Programm zu schreiben, das ein Dreick der Größe n erzeugt. Die Umsetzung ist sehr
direkt:
pascalsTriangle :: Int -> Array (Int,Int) Int
pascalsTriangle n = a
where a = array ((0,0),(n,n)) (
[((i,j),0) | i

5.8. Vertiefung: Rolle der Auswertungsreihenfolge 115
wobei n! = 1 · 2 · . . . · n die Fakultät von n ist. Denkaufgabe: Wie rechnet man die obige Formel
geschickt aus? Auch die Randwerte
!
!
!
i
0
= 1,
i
i
= 1,
i
j
= 0 für i < j
und die Beziehung
!
i
=
j
!
i − 1
+
j
!
i − 1
,
j − 1
die wir bei der Konstruktion des Pascalschen Dreiecks verwendet haben, lassen sich bezüglich dieser
Interpretation deuten. Überlegen! Summieren wir die Elemente der n-ten Zeile, erhalten wir gerade
2 n . Warum?
5.8. Vertiefung: Rolle der Auswertungsreihenfolge
Wir sind bei unseren Überlegungen bisher stillschweigend davon ausgegangen, daß alle
Ausdrücke ganz ausgerechnet werden müssen. Diese Annahme haben wir zum Beispiel
beim Aufstellen der Rekursionsgleichungen für insertionSort gemacht:
T ime(insertionSort (a:x)) = 3 + T ime(insertionSort x ⇒ v) + T ime(insert a v)
Zur Erinnerung: Mit T ime(e ⇒ v) haben wir die Anzahl der Schritte bezeichnet, um den
Ausdruck e zum Wert v auszurechnen. Die obige Gleichung setzt somit voraus, daß wir
insertionSort x in toto ausrechnen müssen, um insert a (insertionSort x)
ausrechnen zu können. Ist diese Annahme gerechtfertigt? Um mit Radio Eriwan zu antworten:
„Im Prinzip ja, aber . . . “. Es kommt darauf an, ob wir die gesamte sortierte Liste
benötigen. Nehmen wir an, wir wollen das Minimum einer Liste von ganzen Zahlen berechnen.
Hier ist eine einfache Lösung:
minimum :: [Integer] -> Integer
minimum x = head (insertionSort x)
Unter der — hier falschen — Annahme, daß alle Ausdrücke ausgerechnet werden müssen,
erhalten wir Θ(n log n) als „worst case“-Laufzeit von minimum. Rechnen wir nur das aus,
was wirklich benötigt wird, beträgt die Laufzeit Θ(n): Um insert a x ausrechnen zu
können, muß x die Form [] oder _:_ haben; dann kann insert a x in konstanter Zeit
ebenfalls zu einer Liste dieser Form ausgerechnet werden.
Wie wird nun in Haskell gerechnet? Es ist in der Tat so, daß jeder Ausdruck nur dann
ausgerechnet wird, wenn er im Laufe der Rechnung benötigt wird. Aus diesem Grund
ist die Laufzeit unter Umständen besser als unsere Rechnungen dies vermuten lassen.
Ein Beispiel: Um den Ausdruck let x=e in e’ auszurechnen, rechnen wir zunächst e’

116 5. Effizienz und Komplexität
aus. Stellen wir dabei fest, daß wir den Wert von x benötigen, werten wir e in einer
Nebenrechnung aus und setzen das Ergebnis für x ein. Benötigt wird x z.B., wenn wir eine
Fallunterscheidung durchführen müssen, case x of {...}, oder wenn x Argument
arithmetischer Operationen ist: x*x. Auf diese Weise wird e höchstens einmal ausgerechnet.
Sollten wir auf die Idee kommen, e für jedes Auftreten von x neu auszurechnen, kann sich die
Rechenzeit und der Platzbedarf dramatisch erhöhen. Eine Mehrfachungauswertung könnte aus Versehen
vorkommen, wenn wir e unausgewertet für x in e’ einsetzen — die let-Regel wird zu früh
angewendet — und mechanisch weiterrechnen.
Analysieren wir zur Illustration des Offensichtlichen die Funktion power aus Abschnitt 3.2.3. Der
Wert von y in let {y = power x (n ‘div‘ 2)} in ... wird offenbar benötigt. Die Laufzeit
von power x n ist abhängig vom Exponenten n; wir zählen die Anzahl der Multiplikationsoperationen.
Zunächst die Analyse des tatsächlichen Verhaltens:
T power(0) = 0
T power(2n − 1) = T power(n − 1) + 2 für n > 0
T power(2n) = T power(n) + 1 für n > 0
Eine geschlossene Form für T power(n) läßt sich gut bestimmen, wenn wir n binär darstellen, z.B. 13 =
(1101)2. Mit jedem rekursiven Aufruf wird das letzte Bit, das „least significant bit“, abgeknipst. Ist
es 0, erhöhen sich die Kosten um eins, ist es 1 entsprechend um zwei. Wir erhalten:
T power(n) = ⌊log 2 n⌋ + ν(n) + 1 ∈ Θ(log n) für n > 0,
wobei ν(n) gleich der Anzahl der Einsen in der Binärrepräsentation von n ist. Der Platzbedarf von
power ist ebenfalls Θ(log n).
Nehmen wir nun an, daß wir den Wert von y für jedes Vorkommen neu ausrechnen. Dann ergeben
sich folgende Kostengleichungen:
T ′
power(0) = 0
T ′
power(2n − 1) = 2T ′
power(n − 1) + 2 für n > 0
T ′
power(2n) = 2T ′
power(n) + 1 für n > 0
Lösen wir die Rekurrenzgleichungen auf, erhalten wir
T ′
power(n) = Θ(n) für n > 0.
Wir sehen: Wenn wir naiv rechnen, erhöht sich die Laufzeit und unter Umständen auch der Platzbedarf
drastisch, nämlich exponentiell.

6. Abstraktion
6.1. Listenbeschreibungen
Listen sind die am häufigsten verwendete Datenstruktur. Aus diesem Grund lohnt es sich,
weitere Notationen einzuführen, die die Konstruktion und die Verarbeitung von Listen
vereinfachen. So erlaubt Haskell z.B. die Notation arithmetischer Folgen:
[1 ..] Liste der positiven Zahlen,
[1 .. 99] Liste der positiven Zahlen bis einschließlich 99,
[1, 3 ..] Liste der ungeraden, positiven Zahlen,
[1, 3 .. 99] Liste der ungeraden, positiven Zahlen bis einschließlich 99.
Die Listen sind jeweils vom Typ [Integer]. Die untere und die obere Grenze können
durch beliebige Ausdrücke beschrieben werden. Die Schrittweite ergibt sich als Differenz
des ersten und zweiten Folgenglieds.
Um Funktionen auf Listen zu definieren, haben wir bis dato rekursive Gleichungen verwendet.
Manchmal können listenverarbeitende Funktionen einfacher und lesbarer mit
Listenbeschreibungen programmiert werden. Schauen wir uns ein paar Beispiele an: Die
Liste der ersten hundert Quadratzahlen erhält man mit
squares’’ :: [Integer]
squares’’ = [n*n | n

118 6. Abstraktion
Die vordefinierte Funktion or verallgemeinert die logische Disjunktion auf Listen Boolescher
Werte.
Mit Hilfe einer Listenbeschreibung können auch Elemente einer Liste mit bestimmten
Eigenschaften ausgewählt werden. Die Funktion divisors n bestimmt die Liste aller
Teiler von n. Mit ihrer Hilfe läßt sich gut beschreiben, wann eine Zahl eine Prinzahl ist: n
ist prim, wenn divisors n==[1,n]. Beachte: 1 ist keine Primzahl.
divisors’ :: (Integral a) => a -> [a]
divisors’ n = [d | d [a]
primes’ = [n | n [a] -> [a]
sieve (a:x) = a:sieve [n | n [a]
primes’’ = sieve [2..]
Ein bekanntes Sortierverfahren, Quicksort von C.A.R. Hoare, läßt sich gut mit Hilfe von
Listenbeschreibungen definieren.
qsort’’’ :: (Ord a) => [a] -> [a]
qsort’’’ [] = []
qsort’’’ (a:x) = qsort’’’ [b | b

6.1. Listenbeschreibungen 119
Die Variable a wird zunächst mit 0 belegt, b nimmt nacheinander die Werte von 1 bis 3
an. Der Ausdruck im Kopf wird jeweils bezüglich dieser Belegungen ausgerechnet. Man
sieht: Weiter rechts stehende Generatoren variieren schneller.
Genau wie ein let-Ausdruck führt auch ein Generator neue Variablen ein. Die Sichtbarkeit
dieser Variablen erstreckt sich auf den Kopf und auf weiter rechts stehende Generatoren
und Filter. Die Funktion concat, die eine Liste von Listen konkateniert, illustriert
dies.
concat’ xs = [a | x

120 6. Abstraktion
Die Hilfsfunktion place erhält vier Argumente: die Nummer der aktuellen Spalte, die
Liste der noch nicht verwendeten Reihenpositionen und die Nummern der bereits belegten
auf- und absteigenden Diagonalen.
place :: Integer -> [Integer] -> [Integer] -> [Integer] -> [Board]
place c [] ud dd = [[]]
place c rs ud dd = [q:qs | q

6.2. Funktionen höherer Ordnung 121
rep’ n a = [a | i Bool) -> [a] -> [a]
isortBy (

Übung 6.1 Mit isortBy lassen sich Listen beliebigen Typs sortieren,
auch Listen auf Funktionen. Warum muß a nicht Instanz
von Ord sein? sortieren:
Übung 6.2 Definiere mergeBy und msortBy.
122 6. Abstraktion
isort [] = []
isort (a:x) = insert a (isort x)
insert a [] = [a]
insert a x@(b:y)
| a components p dateOfBirth p

6.2. Funktionen höherer Ordnung 123
sucht ein Element in einem geordneten Feld. In Analogie zu den Sortierfunktionen könnten
wir die zugrundeliegende Vergleichsoperation zum Parameter machen. Aber es geht
noch sehr viel allgemeiner: Betrachten wir die Funktionsdefinition von binarySearch
genauer: Die Vergleichsoperation compare wird nur in dem Ausdruck compare e (a!m)
verwendet; von Aufruf zu Aufruf ändert sich jedoch lediglich m. Von daher liegt es nahe,
die Binäre Suche mit einer Funktion zu parametrisieren, die m direkt auf ein Element von
Ordering abbildet. Daß wir in einem Feld suchen, tritt nunmehr in den Hintergrund.
Indem wir das Suchintervall übergeben, beseitigen wir die Abhängigkeit ganz. Noch eine
letzte Änderung: Sind wir bei der Suche erfolgreich, geben wir m in der Form Just m
zurück; anderenfalls wird Nothing zurückgegeben.
binarySearchBy :: (Integral a) => (a -> Ordering) -> (a,a) -> Maybe a
binarySearchBy cmp = within
where within (l,r) = if l > r then Nothing
else let m = (l+r) ‘div‘ 2
in case cmp m of
LT -> within (l, m-1)
EQ -> Just m
GT -> within (m+1, r)
Die Funktion binarySearchBy implementiert das folgende „Spiel“: Der Rechner fordert
die Benutzerin auf, sich eine Zahl zwischen l und r auszudenken. Der Rechner rät:
„Ist die gesuchte Zahl m?“. Die Benutzerin sagt, ob die Zahl gefunden wurde, ob sie kleiner
oder größer ist. Nach Θ(log(r − l)) Schritten weiß der Rechner die Lösung — falls
bei den Antworten nicht gemogelt wurde. Im Programm entspricht die Funktion cmp der
Benutzerin: Ist x die ausgedachte Zahl, so beschreibt cmp = \i -> compare x i ihr
Verhalten. Liegt x im Intervall (l,r), so ergibt binarySearchBy cmp (l,r) gerade
Just x.
Was heißt es eigentlich, daß bei den Antworten gemogelt wird? Anders gefragt: Welche
Anforderungen muß cmp erfüllen, damit die Binäre Suche vernünftig arbeitet? Nun — wir
erwarten, daß es höchstens ein Element k gibt mit cmp k = EQ, für alle i < k muß
cmp i = GT gelten, für alle j > k entsprechend cmp j = LT. Die Funktion cmp unterteilt
(l, r) somit maximal in drei Bereiche:
l . . . k − 1
GT
k
EQ
k + 1 . . . r
LT
Umfaßt der mittlere Bereich mehr als ein Element, funktioniert die Binäre Suche auch.
In diesem Fall wird irgendein Element aus dem mittleren Drittel zurückgegeben. Formal
muß cmp lediglich antimonoton sein: i j ⇒ cmp i cmp j mit LT < EQ < GT. Aufgabe:
Verallgemeinere die Binäre Suche, so daß sie gerade das mittlere Drittel als Intervall
bestimmt.

124 6. Abstraktion
Wie immer, wenn man eine Funktion verallgemeinert, ist es interessant zu sehen, wie
man die ursprüngliche Funktion durch Spezialisierung der Verallgemeinerung erhält:
binSearch a e = case r of Nothing -> False; Just _ -> True
where r = binarySearchBy (\i -> compare e (a!i)) (bounds a)
Als weitere Anwendung stellen wir uns die Aufgabe, zu einem englischen Begriff die
deutsche Übersetzung herauszusuchen. Das der Suche zugrundeliegende und aus Platzgründen
sehr klein geratene Wörterbuch stellen wir als Feld dar:
englishGerman :: Array Int (String, String)
englishGerman = listArray (1,2) [("daffodil", "Narzisse"),
("dandelion","Loewenzahn")]
Das Englisch-Deutsch-Wörterbuch ist naturgemäß nach den englischen Wörtern geordnet;
es taugt nicht als Deutsch-Englisch-Wörterbuch. Übung: Programmiere eine Funktion,
die ein X-Y-Wörterbuch in ein Y-X-Wörterbuch überführt. Die Funktion german
realisiert die Übersetzung:
german :: [Char] -> Maybe [Char]
german x = case r of Nothing -> Nothing
Just m -> Just (snd (englishGerman!m))
where r = binarySearchBy (\i -> compare x (fst (englishGerman!i)))
(bounds englishGerman)
Der zu übersetzende Begriff wird jeweils mit dem englischen Wort verglichen, bei erfolgreicher
Suche wird das deutsche Wort zurückgegeben.
Wenn nur die linke Grenze des Suchintervalls gegeben ist, können wir die Binären Suche leicht
variieren: Zunächst wird die rechte Intervallgrenze bestimmt, also ein beliebiges Element r mit
cmp r = LT. Als Kandidaten werden nacheinander l, 2l, 4l, . . . herangezogen; der Suchraum wird
somit in jedem Schritt verdoppelt. Ist ein r gefunden, folgt eine normale Binäre Suche.
openbinSearchBy :: (Integral a) => (a -> Ordering) -> a -> Maybe a
openbinSearchBy cmp l = lessThan l
where lessThan r = case cmp r of
LT -> binarySearchBy cmp (l,r)
EQ -> Just r
GT -> lessThan (2*r)
Die Suche im offenen Intervall terminiert natürlich nicht, wenn es kein r mit cmp r = LT gibt.

6.2. Funktionen höherer Ordnung 125
6.2.2. Rekursionsschemata
In Abschnitt 4.2 haben wir das Schema der strukturellen Rekursion auf Listen eingeführt.
Der Motor des Schemas ist der Rekursionsschritt. Zitat: „Um das Problem für die Liste
a:x zu lösen, wird [. . . ] zunächst eine Lösung für x bestimmt, die anschließend zu einer
Lösung für a:x erweitert wird.“ Überlegen wir noch einmal genauer, was im Rekursionsschritt
zu tun ist: Gegeben ist eine Lösung s, unter Verwendung von a und x gilt es, eine
Gesamtlösung s’ zu konstruieren. Im Prinzip müssen wir eine Funktion angeben, die a,
x und s auf s’ abbildet. Dies erkannt, kann man das Rekursionsschema mit Hilfe einer
Funktion höherer Ordnung programmieren; aus dem Kochrezept wird ein Programm:
structuralRecursionOnLists :: solution -- base
-> (a -> [a] -> solution -> solution) -- extend
-> [a] -> solution
structuralRecursionOnLists base extend = rec
where rec [] = base
rec (a:x) = extend a x (rec x)
Auf diese Weise läßt sich das Rekursionsschema formal definieren; wenn Zweifel bestehen,
ob eine gegebene Funktion strukturell rekursiv ist, können diese ausgeräumt werden,
indem man die Funktion in Termini von sROL formuliert oder zeigt — was ungleich
schwerer ist —, daß dies nicht möglich ist.
Obwohl denkbar wird nicht empfohlen, sROL bei der Programmierung zu verwenden
— im nächsten Abschnitt lernen wir eine abgemagerte Variante kennen, die im Programmieralltag
ihren festen Platz hat. Dessen ungeachtet wollen wir uns trotzdem anschauen,
wie die Funktionen isort und insert — die ersten, die wir nach dem Kochrezept der
Strukturellen Rekursion gebraut haben — mit Hilfe von sROL formuliert werden.
isort’ :: (Ord a) => [a] -> [a]
isort’ = structuralRecursionOnLists
[]
(\a _ s -> insert’’ a s)
insert’’ :: (Ord a) => a -> [a] -> [a]
insert’’ a = structuralRecursionOnLists
[a]
(\b x s -> if a ... jeweils die
Lösung von x darstellt: In der Definition von isort ist s gleich isort x, in der Definition

Übung 6.3 Schreibe perms und insertions als Anwendungen
des Rekursionsschemas um.
Übung 6.4 Diskutiere Vor- und Nachteile beider Spezifikationen.
126 6. Abstraktion
von insert ist s gleich insert a x. Bei der letztgenannten Funktion nutzen wir aus,
daß die Funktion gestaffelt ist: nicht insert wird strukturell rekursiv definiert, sondern
insert a. Knobelaufgabe: Wie ändert sich die Definition, wenn man die Parameter von
insert vertauscht?
Programmiert man tatsächlich Funktionen mit Hilfe von sROL, wird man gezwungen,
sich genau an das Rekursionsschema zu halten. Insbesondere wenn man mit der Strukturellen
Rekursion noch nicht per Du ist, erweist sich dieses Diktat oftmals als lehrreich.
Bewahrt es uns doch insbesondere davor, ad-hoc Lösungen zu formulieren.
Nehmen wir die Gelegenheit wahr und schauen uns noch ein Beispiel zur Strukturellen
Rekursion an: Es gilt die Liste aller Permutationen einer gegeben Liste zu bestimmen. Die
Liste [2,6,7] z.B. läßt sich auf sechs verschiedene Arten anordnen. Strukturell rekursiv
erhält man sie wie folgt: Wir dürfen annehmen, daß wir das Problem für die Restliste
[6,7] bereits gelöst haben: [[6,7], [7,6]] ist die gesuchte Liste der Permutationen.
Jede einzelne Permutation müssen wir um das Element 2 erweitern. Aber — an welcher
Position fügen wir es ein? Aus der Aufgabenstellung leitet sich ab, daß alle Positionen zu
berücksichtigen sind. Also, aus der Liste [6,7] werden [2,6,7], [6,2,7] und [6,7,2]
und aus [7,6] erhalten wir [2,7,6], [7,2,6] und [7,6,2]. Das Einfügen an allen
Positionen „riecht“ nach einer Teilaufgabe, die wir wiederum strukturell rekursiv lösen.
Überlegen! Das Aufsammeln der Teillösungen erledigen wir mit Listenbeschreibungen.
Schließlich müssen wir uns noch Gedanken über die Rekursionsbasis machen: Es gibt nur
eine Permutation der leeren Liste, die leere Liste selbst.
perms :: [a] -> [[a]]
perms [] = [[]]
perms (a:x) = [z | y [[a]]
insertions a [] = [[a]]
insertions a x@(b:y) = (a:x):[b:z | z [a] -> [a]
sort x = head [s | s

6.2. Funktionen höherer Ordnung 127
Auch das Teile- und Herrsche-Prinzip läßt sich mit Hilfe einer Funktion höherer Ordnung
definieren. Vier Bausteine werden benötigt: Eine Funktion, die entscheidet, ob ein
Problem einfach ist; eine Funktion, die ein einfaches Problem löst; eine Funktion, die ein
Problem in Teilprobleme zergliedert und schließlich eine Funktion, die Teillösungen zu
einer Gesamtlösung zusammenführt.
divideAndConquer :: (problem -> Bool) -- easy
-> (problem -> solution) -- solve
-> (problem -> [problem]) -- divide
-> ([solution] -> solution) -- conquer
-> problem -> solution
divideAndConquer easy solve divide conquer = rec
where rec x = if easy x then solve x
else conquer [rec y | y [a] -> [a]
msort’’ = divideAndConquer
(\x -> drop 1 x == [])
(\x -> x)
(\x -> let k = length x ‘div‘ 2 in [take k x, drop k x])
(\[s,t] -> merge s t)
Im Fall Quicksort ist es umgekehrt: Nur in der Teile-Phase werden Elemente verglichen;
in der Herrsche-Phase werden die sortierten Teillisten lediglich aneinandergefügt.
qsort :: (Ord a) => [a] -> [a]
qsort = divideAndConquer
(\x -> drop 1 x == [])
(\x -> x)
(\(a:x) -> [[ b | b x++y++z)

128 6. Abstraktion
6.2.3. foldr und Kolleginnen
Magert man die strukturelle Rekursion auf Listen etwas ab, erhält man ein Rekursionsschema,
das im Programmieralltag seinen festen Platz hat. Schauen wir uns zunächst einmal
zwei einfache strukturell rekursive Funktionen an.
sum’’ :: (Num a) => [a] -> a
sum’’ [] = 0
sum’’ (a:x) = a + sum’’ x
or’’ :: [Bool] -> Bool
or’’ [] = False
or’’ (a:x) = a || or’’ x
Übung 6.5 Definiere die Funktionen product und and, die
eine Liste ausmultiplizieren bzw. ver„und“en. Inwiefern sind sum und or besonders einfach? Nun, im Rekursionsschritt wird nur das
Kopfelement a mit der Teillösung s kombiniert; der Listenrest x wird nicht benötigt. Diese
Eigenschaft teilen die Funktionen mit isort, nicht aber mit insert. Vergleichen! Das
abgemagerte Rekursionsschema nennt sich foldr. Wie der Name motiviert ist, erklären
wir gleich, zunächst die Definition:
foldr’ :: (a -> solution -> solution) -> solution -> [a] -> solution
foldr’ (*) e = f
where f [] = e
f (a:x) = a * f x
Man sieht: Die Vereinfachung besteht darin, daß wir den dreistelligen Parameter extend
durch den zweistelligen Parameter (*) ersetzt haben, den wir aus Gründen der Übersichtlichkeit
zusätzlich infix notieren. [Aus historischen Gründen wird die Induktionsbasis erst
als zweites Argument angegeben.] Die Definitionen von sum und or werden zu Einzeilern,
wenn foldr verwendet wird.
sum’ = foldr (+) 0
product’ = foldr (*) 1
and’ = foldr (&&) True
or’ = foldr (||) False
Die Arbeitsweise von foldr kann man sich einfach merken: foldr ersetzt den Listenkonstruktor
(:) durch (*) und die leere Liste [] durch e; aus der Liste a1:(a2:· · ·:(an−1
:(an:[]))· · ·) wird der Ausdruck a1*(a2*· · ·:(an−1*(an:e))· · ·). Man sagt auch, die
Liste wird aufgefaltet. Der Buchstabe r im Namen deutet dabei an, daß der Ausdruck wie
auch die ursprüngliche Liste rechtsassoziativ geklammert wird. Eine Kollegin von foldr,
deren Namen mit l endet, lernen wir in Kürze kennen. Schauen wir uns vorher noch ein
paar Beispiele an:

6.2. Funktionen höherer Ordnung 129
isort = foldr insert []
length = foldr (\n _ -> n + 1) 0
x ++ y = foldr (:) y x
reverse = foldr (\a x -> x ++ [a]) []
concat = foldr (++) []
Um es noch einmal zu betonen: Das erste Argument von foldr definiert den Rekursionsschritt,
das zweite Argument die Rekursionsbasis. Knobelaufgabe: Was macht die
folgende Funktion:
mystery x = foldr (\a -> foldr () [a]) [] x
where a (b:x) = if a b * a. Aus dieser Eigenschaft und unter Verwendung der
Definition von reverse aus Abschnitt 5.5.2 läßt sich die folgende Definition von foldl
ableiten.
foldl’’ :: (solution -> a -> solution) -> solution -> [a] -> solution
foldl’’ (*) e x = f x e
where f [] e = e
f (a:x) e = f x (e*a)

130 6. Abstraktion
Die Hilfsfunktion f korrespondiert dabei mit der Hilfsfunktion revTo. Einziger Unterschied:
der Listenkonstruktor (:) wird sogleich durch flip (*) ersetzt. Spezialisieren
wir foldl wieder, erhalten wir eine effiziente Definition von reverse.
reverse’’’ = foldl (flip (:)) []
Kommen wir zu weiteren Anwendungen: sum, or, concat etc. können auch via foldl
definiert werden:
sum’’’ = foldl (+) 0
or’’’ = foldl (||) False
concat’’’ = foldl (++) []
Daß die Definitionen äquivalent zu den ursprünglichen sind, liegt daran, daß (+) und
0, (&&) und False, (++) und [] jeweils ein Monoid formen: Die Operation ist assoziativ
und das Element ist neutral bezüglich der Operation. Natürlich stellt sich die Frage,
welcher Definition der Vorzug zu geben ist. Also, wie ist es jeweils um den Speicher- und
Zeitbedarf bestellt? Vergleichen wir folgende Rechnungen:
sum [1..9] sum’ [1..9]
⇒ f [1..9] ⇒ f’ [1..9] 0
⇒ 1 + f [2..9] ⇒ f’ [2..9] 1
⇒ 1 + (2 + f [3..9]) ⇒ f’ [3..9] 3
. . . . . .
⇒ 1 + (2 + ... + (9 + f [])) ⇒ f’ [] 45
⇒ 1 + (2 + ... + (9 + 0)) ⇒ 45
⇒ 45
Die Anzahl der Schritte ist gleich, aber der Platzbedarf ist unterschiedlich. Wird foldr
verwendet, entsteht ein arithmetischer Ausdruck, der proportional zur Länge der Liste
wächst. Erst im letzten Schritt kann der Ausdruck ausgerechnet werden. Wird sum mit
foldl definiert, ist der Platzbedarf hingegen konstant, da die arithmetischen Ausdrücke
in jedem Schritt vereinfacht werden können. 1 Im Fall von or erweist sich die Definition
1 Tatsächlich muß man bei der Auswertung der Teilausdrücke etwas nachhelfen.

6.2. Funktionen höherer Ordnung 131
mit foldr als besser:
or [False,True,False] or’ [False,True,False]
⇒ f [False,True,False] ⇒ f’ [False,True,False] False
⇒ False || f [True,False] ⇒ f’ [True,False] (False || False)
⇒ f [True,False] ⇒ f’ [True,False] False
⇒ True || f [False] ⇒ f’ [False] (True || False)
⇒ True ⇒ f’ [False] True
⇒ f’ [] (False || True)
⇒ f’ [] True
⇒ True
Im Unterschied zur Addition läßt sich die logische Disjunktion auch ausrechnen, wenn
lediglich der erste Parameter bekannt ist. Ist dieser gleich True wird der zweite Parameter
zudem gar nicht benötigt. Aus diesem Grund wird die Liste Boolescher Werte nur bis zum
ersten True durchlaufen. Auch im Fall von concat ist foldr der Gewinner — aus den
gleichen Gründen, aus denen (++) als rechtsassoziativ vereinbart wird.
Nicht immer ist die leere Liste eine geeignete Induktionsbasis: Nehmen wir an, wir
wollen das kleinste Element einer Liste bestimmen. Was ist das kleinste Element der leeren
Liste? Als Induktionsbasis wird hier sinnvollerweise die einelementige Liste gewählt. Die
Funktionen foldr1 und foldl1 realisieren das entsprechende Rekursionsschema. Wir
geben nur die Typen an und überlassen die Definition der geneigten Leserin.
foldr1 :: (a -> a -> a) -> [a] -> a
foldl1 :: (a -> a -> a) -> [a] -> a
Wie foldr erzeugt auch foldr1 einen rechtsentarteten „Ausdrucksbaum“. Nur — die
Blätter bestehen ausschließlich aus Listenelementen, aus diesem Grund ist der Typ auch
etwas spezieller. Einen „richtigen“ rechts- oder linksentarteten Baum können wir erzeugen,
indem wir als Operator den Konstruktor Br angeben. Da binäre Bäume — so wie wir
sie definiert haben — nicht leer sind, müssen wir als Induktionsbasis die einelementige
Liste verwenden.
righty, lefty :: [a] -> Tree a
righty = foldr1 Br . map Leaf
lefty = foldl1 Br . map Leaf
Verschiedene Probleme, verschiedene Lösungen: Wir haben gesehen, daß je nach Aufgabenstellung
Anwendungen von foldr und foldl sich stark im Zeit- und Platzbedarf
unterscheiden. Manchmal ist foldr die gute Wahl, manchmal ihre Kollegin foldl. Natürlich
gibt es auch Fälle, in denen foldr und foldl gleichermaßen ungeeignet sind:
Betrachten wir z.B. die Aufgabe, eine Liste von Läufen zu fusionieren. Ein verwandtes

132 6. Abstraktion
Problem haben wir bereits einer ausführlichen Analyse unterzogen: Man erinnere sich an
die Funktion mergeTree aus Abschnitt 5.2, die einen Baume in eine sortierte Liste überführt.
Die Analyse ergab, daß mergeTree ausgeglichene Bäume bevorzugt. Damit ist klar,
daß weder foldr merge [] noch foldl merge [] gute Lösungen für das obige Problem
darstellen. Es liegt nahe, foldr und foldl ein weiteres Rekursionsschema foldm
an die Seite zu stellen, das einen ausgeglichenen Ausdrucksbaum erzeugt: aus der Liste
a1:(a2:· · ·:(an−1:(an:[]))· · ·) wird der Ausdruck
(· · ·(a1 * a2)· · · * · · ·(ai−1 * ai)· · ·) * (· · ·(ai+1 * ai+2)· · · * · · ·(an−1 * n)· · ·)
mit i = ⌊n/2⌋. Der Ausdrucksbaum verdeutlicht die Struktur besser:
: *
/ \ / \
a1 : * *
/ \ foldm (*) e / \ / \
a2 .. ------------> .. .. .. ..
\ / \ / \
: * * ... * *
/ \ / \ / \ / \ / \
an [] a1 a2 ai-1 ai ai+1 ai+2 an-1 an
Die Implementierung von foldm ist aufwendiger als die ihrer Kolleginnen. Das ist auch
klar, da wir sozusagen „gegen“ die rechtsassoziative Listenstruktur arbeiten. Allerdings
müssen wir das Rad nicht neu erfinden, denn — etwas ähnliches haben wir schon programmiert:
die Funktion build aus Abschnitt 3.4 überführt eine Liste in einen ausgeglichenen
Baum. Ersetzen wir in der Definition von build den Konstruktor Br durch den
Operator (*), erhalten wir im wesentlichen die Definition von foldm:
foldm :: (a -> a -> a) -> a -> [a] -> a
foldm (*) e [] = e
foldm (*) e x = fst (f (length x) x)
where f n x = if n == 1 then (head x, tail x)
else let m = n ‘div‘ 2
(a,y) = f m x
(b,z) = f (n-m) y
in (a*b,z)
foldm1 (*) = foldm (*) (error "foldm1 []")
Mit Hilfe von foldm läßt sich die anfangs gestellte Aufgabe effizient lösen. Die Funktion
balanced entspricht gerade der Funktion build.

6.2. Funktionen höherer Ordnung 133
mergeList :: (Ord a) => [[a]] -> [a]
mergeList = foldm merge []
balanced :: [a] -> Tree a
balanced = foldm1 Br . map Leaf
Mit der Funktion mergeList sind wir schon fast wieder beim Sortierproblem angelangt:
Die top-down Variante von msort und ihre „geschmeidige“ Verbesserung smsort
lassen sich mit foldm erschreckend (?) kurz formulieren.
msortBy, smsortBy :: (a -> a -> Bool) -> [a] -> [a]
msortBy ( b) -> Tree a -> b
foldTree leaf br = f
where f (Leaf a) = leaf a
f (Br l r) = br (f l) (f r)
Viele Funktionen auf Bäumen lassen sich kurz und knapp mit foldTree definieren.
size’ = foldTree (\a -> 1) (+)
depth’ = foldTree (\a -> 0) (\m n -> max m n + 1)
mergeTree’ = foldTree (\a -> [a]) merge
mergeRuns’ = foldTree id merge Übung 6.6 Definiere mit Hilfe von foldTree die Funktion
branches :: Tree a -> Int, die die Anzahl der Verzeigungen
in einem Baum bestimmt.
6.2.4. map und Kolleginnen
Die Funktion map, die eine Funktion auf alle Elemente einer Liste anwendet, haben wir
schon kennengelernt. Hier ist noch einmal ihre Definition:
map :: (a -> b) -> [a] -> [b]
map f [] = []
map f (a:x) = f a:map f x
Übung 6.7 Wie läßt sich foldm auf foldTree und build zurückführen?
Welcher Zusammenhang besteht zwischen struktureller
Rekursion auf Bäumen und dem Rekursionsschema
foldTree?

134 6. Abstraktion
Ein ideales Anwendungsgebiet für map und ihre Kolleginnen sind Operationen auf Vektoren
und Matrizen. Einen Vektor stellen wir einfach durch eine Liste dar — Felder wären
eine Alternative, die wir aber nicht verfolgen, da wir auf die Vektorelemente nie direkt
zugreifen müssen. Eine Matrix repräsentieren wir durch eine Liste von Zeilenvektoren.
type Vector a = [a]
type Matrix a = [Vector a]
Die Matrix 3 8 0
2 17 1
wird z.B. durch den Ausdruck
[[3,8,0],[2,17,1]]
dargestellt. Als erste Operation realisieren wir die Multiplikation eines Skalars mit einem
Vektor (für die Notation der Operationen erfinden wir eine Reihe von Operatoren).
():: (Num a) => a -> Vector a -> Vector a
k x = map (\a -> k*a) x
Um die Summe und das innere Produkt zweier Vektoren zu programmieren, erweist
sich eine Kollegin von map als hilfreich, die eine zweistellige, gestaffelte Funktion auf zwei
Listen anwendet.
zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]
zipWith f (a:x) (b:y) = f a b:zipWith f x y
zipWith _ _ _ = []
Die Funktion heißt auf englisch Reißverschluß, da f wiederholt jeweils auf die beiden
ersten Listenelemente angewendet wird. Beachte: Die Argumentlisten müssen nicht die
gleiche Länge haben; die kürzere bestimmt die Länge der Ergebnisliste. Summe und inneres
Produkt zweier Vektoren sind schnell definiert.
() :: (Num a) => Vector a -> Vector a -> Vector a
x y = zipWith (+) x y
() :: (Num a) => Vector a -> Vector a -> a
x y = sum (zipWith (*) x y)
Ein nützlicher Spezialfall von zipWith ist zip: die zweistellige Operation ist hier der
Paarkonstruktor.
zip :: [a] -> [b] -> [(a,b)]
zip = zipWith (\a b -> (a,b))

6.2. Funktionen höherer Ordnung 135
Die Funktion zip wird oft in Verbindung mit Listenbeschreibungen verwendet. Hier sind
noch einmal alle Vektoroperationen unter Verwendung von Listenbeschreibungen definiert.
k x = [k*a | a Matrix a
a b = zipWith () a b
Das Produkt zweier Matrizen A und B erhalten wir, indem wir jede Zeile von A mit jeder
Spalte von B multiplizieren. Genauer: Ist x ein Zeilenvektor von A, so ist der entsprechende
Zeilenvektor der Produktmatrix gleich [ x y | y Matrix a -> Matrix a -> Matrix a
m n = [[x y | y

136 6. Abstraktion
Die Mogelei hat tatsächlich auch einen Vorteil: transpose kann auch mit Teillisten arbeiten,
die unendlich lang sind. Dieser Fall tritt bei den hier betrachteten Matrizenoperationen nicht auf;
in anderen Anwendungen aber sehr wohl. Die Listen könnten z.B. Meßreihen sein; mit Hilfe von
transpose können diese als Tabellen ausgegeben werden: Bei der Ausgabe der Liste x = [[1..],
[2..],[3..]] wird die zweite Teilliste niemals erreicht; transpose x macht aus den drei unendlichen
Listen eine unendliche Liste von dreielementigen Listen, die ohne Probleme ausgegeben
werden kann.
Die folgende Variante von transpose verarbeitet auch obere Dreiecksmatrizen der Form [[1,2,
3],[4,5],[6]]; das Ergebnis ist wieder eine obere Dreiecksmatriz, bei der nur die Enträge oberhalb
der Diagonalen aufgeführt werden.
transpose’’ = foldr (\v vs -> zipWith (:) v (vs ++ repeat [])) []
Interessanterweise verarbeiten auch die Addition und Multiplikation — sofern sie
diese Variante von transpose verwendet — obere Dreieickmatrizen fehlerfrei. Warum?
Übung: Nachfolgend ist eine dritte Variante von transpose aufgeführt. Diskutiere Vor- und
Nachteile der drei Definitionen.
transpose’’’ a
| and (map null a) = []
| otherwise = map head a:transpose’’’ (map tail a)
Die vordefinierte Funktion null :: [a] -> Bool ergibt True gdw. das Argument die leere
Liste ist.
Das Gauß’sche Eliminationsverfahren:
deleteMax :: (Ord b) => (a -> b) -> [a] -> (a, [a])
deleteMax key [a] = (a,[])
deleteMax key (a:x)
| key a >= key b = (a,x)
| otherwise = (b,a:y)
where (b,y) = deleteMax key x
gaussElim :: (Ord a, Fractional a) => Matrix a -> Matrix a
gaussElim [row] = [row]
gaussElim rows = prow:gaussElim (map elim rows’)
where (prow@(p:ps),rows’) = deleteMax (\row -> abs (head row)) rows
elim (x:xs) = xs ((-x/p) ps)
solve :: (Fractional a) => Matrix a -> Vector a
solve [] = [-1]
solve ((x:xs):rows) = -(solns xs)/x:solns
where solns = solve rows
Zur Übung: Definiere die gleichen Operationen auf Feldern.

6.3. Typklassen 137
6.3. Typklassen
6.3.1. Typpolymorphismus und Typklassen
Im letzten Kapitel haben wir uns mit dem Sortieren von Listen beschäftigt. Um die Algorithmen
vorzustellen und vorzuführen, sind wir stets davon ausgegangen, daß die Listen
Elemente eines (fast) beliebigen Basistyps enthalten. Aus theoretischer Sicht ist dieser Typ
ohne Belang: Beim Nachweis der Korrektheit oder bei der Analyse der asymptotischen
Laufzeit spielt es keine Rolle, ob Zahlen oder Personendaten sortiert werden. Aus praktischer
Sicht ist eine Einschränkung hier wenig annehmbar: Natürlich möchte man sowohl
Zahlen als auch Personendaten sortieren und noch vieles andere mehr. Lisa Lista: Eigentlich ist dies eine Selbstverständlichkeit, oder?
Die Tatsache, daß der Grundtyp der Listen beliebig ist, drücken wir aus, indem wir bei
der Typdeklaration eine Typvariable für den Grundtyp der Listen einsetzen.
(++) :: [a] -> [a] -> [a]
Lies „für alle Typen a ist [a] -> [a] -> [a] ein Typ von (++)“. Beide Argument müssen
somit Listen über dem gleichen Typ sein, dieser ist aber beliebig. Wir sagen, (++) ist
eine polymorphe Funktion. Sie kann für beliebige Ausprägungen von a verwendet werden:
"hello " ++ "world" ⇒ "hello world"
[19, 9] ++ [7] ⇒ [19, 9, 7]
["hello ","world"] ++ ["it’s","me"] ⇒ ["hello ","world","it’s","me"]
Um es noch einmal zu betonen: In beiden Fällen handelt es sich um die gleiche Funktion.
Fast alle der in den letzten Kapiteln definierten Funktionen besitzen einen polymorphen
Typ; hier eine kleine Auswahl:
head :: [a] -> a
tail :: [a] -> [a]
leaves :: Tree a -> [a]
build :: [a] -> Tree a
map :: (a -> b) -> ([a] -> [b])
Der Typ von map ist sehr allgemein: Das erste Argument ist eine beliebige Funktion;
Argument- und Ergebnistyp dieser Funktion sind nicht festgelegt, insbesondere müssen
sie nicht gleich sein: map (\n -> n+1), map (\a -> Leaf a) und auch map map
sind korrekte Aufrufe.
Was ist nun der Typ der Sortierfunktionen? Alle Sortierfunktionen stützen sich auf die
Vergleichsoperation (

138 6. Abstraktion
Auch Listen lassen sich vergleichen, wenn wir die Listenelemente vergleichen können:
[] [a] ein
Typ von isort“. Der Teil (Ord a) => ist ein sogenannter Kontext, der die Ausprägung
der Typvariable a einschränkt. Dabei ist Ord eine einstellige Relation auf Typen, eine
sogenannte Typklasse, die sich durch folgende Regeln beschreiben läßt (wir führen nur
eine Auswahl auf):
Ord Integer
Ord Char
Ord a ∧ Ord b ⇒ Ord (a, b)
Ord a ⇒ Ord [a]
Lies „Integer ist eine Instanz der Typklasse Ord“. Wir haben oben gesehen, wie (

6.3. Typklassen 139
In Haskell sind eine Reihe von Typklassen vordefiniert; die wichtigsten werden wir im
folgenden kennenlernen.
In der Typklasse Show sind alle vordefinierten Typen enthalten; sie stellt Funktionen zur
Verfügung, mit deren Hilfe sich Werte in ihre textuelle Repräsentation überführen lassen.
show :: (Show a) => a -> String
Schauen wir uns einige Anwendungen an:
show 123 ⇒ "123"
show [1, 2, 3] ⇒ "[1, 2, 3]"
show "123" ⇒ "\"123\""
Das letzte Beispiel illustriert, wie Anführungsstriche in einem String untergebracht werden
können; ihnen ist ein Backslash „\“ voranzustellen.
Die Typklasse Eq umfaßt alle Typen, deren Elemente sich auf Gleichheit testen lassen,
das sind alle Typen mit Ausnahme von Funktionen. Die Funktionen unique und element
verwenden den Test auf Gleichheit, ihre allgemeinsten Typen lauten:
unique :: (Eq a) => [a] -> [a]
element :: (Eq a) => a -> [a] -> Bool
Die Typklasse Ord wird für total geordnete Datentypen verwendet; die meisten Funktionen
des letzten Kapitels haben einen Ord-Kontext:
insert :: (Ord a) => a -> [a] -> [a]
merge :: (Ord a) => [a] -> [a] -> [a]
Neben den üblichen Vergleichsoperationen a -> a -> Ordering
Eine geringfügig effizientere Variante der Funktion uniqueInsert läßt sich mit Hilfe von
compare definieren.
uniqueInsert’ a [] = [a]
uniqueInsert’ a x@(b:y) = case compare a b of
LT -> a:x
EQ -> x
GT -> b:uniqueInsert’ a y

Übung 6.9 Warum ist Num keine Untertypklasse von Ord?
140 6. Abstraktion
Typen, auf denen Addition, Subtraktion und Multiplikation definiert sind, gehören zur
Klasse Num. Dazu zählen alle in Haskell vordefinierten numerischen Typen wir Int, Integer,
Float und Double. Verwendet eine Funktion die Grundrechenarten (+), (-) oder (*),
erhält sie einen Num-Kontext.
size :: (Num n) => Tree a -> n
depth :: (Num n, Ord n) => Tree a -> n
Werden die Funktionen in dieser Allgemeinheit nicht benötigt, steht es der Programmiererin
natürlich frei, den Typ einzuschränken; nichts anderes haben wir in den letzten Kapitel
gemacht. Aus Gründen der Effizienz hat man sich z.B. entschlossen, die vordefinierten
Funktionen length, take und drop auf Int zu spezialisieren:
length :: [a] -> Int
take, drop :: Int -> [a] -> [a]
Man unterscheidet zwischen zwei Divisionsoperatoren: der ganzzahligen Division div
und der normalen Division (/). Entsprechend gibt es zwei verschiedene Klassen: Integral
für numerische Typen, die div anbieten, und Fractional für Typen, die (/) anbieten.
Instanzen von Integral sind Int und Integer, Float und Double sind Instanzen von
Fractional. Die Funktion power, die wir in Abschnitt 3.2.3 definiert haben, erhält den
folgenden Typ:
power :: (Num a, Integral b) => a -> b -> a
Der Exponent muß aufgrund der Verwendung von div und mod eine ganze Zahl sein,
die Basis hingegen ist beliebig. In der Definition von power wird zusätzlich der Test auf
Gleichheit verwendet, warum muß Eq b nicht als Kontext aufgeführt werden? Nun, die
Typklassen sind hierarchisch angeordnet: Eine Instanz von Integral muß auch Instanz
von Num sein, eine Instanz von Num muß auch Instanz von Eq sein. Wir sagen Integral
ist eine Untertypklasse von Num. Welchen Sinn würde es auch machen, div ohne (*)
anzubieten?
Eq Show
/ \ /
Ord Num
\ / \
Integral Fractional
Da Integral a somit Eq a umfaßt, muß nur der erste Kontext aufgeführt werden.
6.3.2. class- und instance-Deklarationen
Ausgangspunkt: polymorphe Typen. Motivation für Typklassen:

6.3. Typklassen 141
• Operation wie (==) oder ( Bool
x /= y = not (x == y)
Der Name der Typklasse is Eq, danach folgt eine Typvariable (allgemeine Form C a) (==)
und (/=) sind Methoden der Klasse. Für (/=) ist eine Default-Methode angegeben. Die
Zugehörigkeit zu einer Klasse wird explizit mit Hilfe einer Instanzdeklaration angegeben.
Beispiel: Rationale Zahlen.
instance Eq Rat where
Rat x y == Rat x’ y’ = x*y’ == x’*y
Unschön. Bei jedem Gleichheitstest werden zwei Multiplikationen durchgeführt. Ausweg: ‘smart’
Konstruktor:
rat :: Int -> Int -> Rat
rat x y = norm (x * signum y) (abs y)
where norm x y = let d = gcd x y in Rat (x ‘div‘ d) (y ‘div‘ d)
Wenn wir davon ausgehen, daß Elemente vom Typ Rat immer normiert sind, dann kann die
Standarddefinition von (==) verwendet werden.
Beispiel: Binärbäume:

142 6. Abstraktion
instance (Eq a) => Eq (Tree a) where
Leaf a == Leaf b = a == b
(Br l r) == Br l’ r’ = l == l’ && r == r’
_ == _ = False
Diese Definition wird mit deriving automatisch erzeugt. Allgemeine Form einer Instanzdeklaration:
(C1 β1,...,Cm βm) => C(T α1 . . . αn) mit {β1, . . . , βm} ⊆ {α1, . . . , αn}.
Definition der Typklasse Ord als Untertypklasse von Eq:
class (Eq a) => Ord a where
compare :: a -> a -> Ordering
() :: a -> a -> Bool
max, min :: a -> a -> a
compare x y | x == y = EQ
| x y = compare x y == GT
max x y | x >= y = x
| otherwise = y
min x y | x

6.3. Typklassen 143
Leaf _ String
showChar :: Char -> ShowS

144 6. Abstraktion
showChar = (:)
showString :: String -> ShowS
showString = (++)
Bei der Typklasse Show wird zusätzlich die Bindungsstärke von Operatoren berücksichtigt,
um Klammern zu sparen. Beispiel: unäres Minus (Bindungsstärke 6), vergleiche
[-7,8]
Br (Leaf (-7)) (Leaf 8)
In Abhängigkeit vom Kontext wird -7 mal geklammert mal nicht; 8 wird nie geklammert.
Deshalb gibt es einen zusätzlichen Parameter, der Informationen über den Kontext
überbringt. Definition der Typklasse Show:
class Show a where
showsPrec :: Int -> a -> ShowS
showList :: [a] -> ShowS
showList [] = showString "[]"
showList (a:x) = showChar ’[’ . shows a . showRest x
where showRest [] = showChar ’]’
showRest (a:x) = showString ", " . shows a . showRest x
shows :: (Show a) => a -> ShowS
shows = showsPrec 0
show :: (Show a) => a -> String
show x = shows x ""
showParen :: Bool -> ShowS -> ShowS
showParen b p = if b then showChar ’(’ . p . showChar ’)’ else p
Der Parameter p besagt: Operatoren der Bindungsstärke < p müssen geklammert werden:
0 niemals klammern, 10 immer klammern. Beispiele für Instanzdeklarationen:
instance Show Rat where
showsPrec p (Rat x y) = showParen (p > 9)
(showString "Rat " . showsPrec 10 x
. showsPrec 10 y)
Beispiel: Binärbäume.

6.3. Typklassen 145
instance (Show a) => Show (Tree a) where
showsPrec p Nil = showString "Nil"
showsPrec p (Leaf a) = showParen (p > 9)
(showString "Leaf " . showsPrec 10 a)
showsPrec p (Br l r) = showParen (p > 9)
(showString "Br " . showsPrec 10 l
. showChar ’ ’ . showsPrec 10 r )
Wird statt Br der Infix-Operator :ˆ: verwendet
infix 4 :ˆ:
ändert sich die letzte Gleichung wie folgt:
showsPrec p (l :ˆ: r) = showParen (p > 4)
(showsPrec 5 l . showString " :ˆ: "
. showsPrec 5 r)
Die Klasse Read führen wir nicht auf. Um die Definition verstehen zu können, muß man
schon ein bischen von Parsen kennen. Hier nur die wichtigste Funktion:
read :: (Read a) => String -> a
Problem: Der Übersetzer muß anhand der Typen entscheiden können, welche Instanzen
gemeint sind. Die folgende Definition erweist sich als problematisch:
whoops :: String -> String
whoops x = show (read x)
Abhilfe: explizite Typangabe:
whoops :: String -> String
whoops x = show (read x :: Tree Int)
6.3.5. Die Typklasse Num
Definition der Typklasse Num:
class (Eq a, Show a) => Num a where
(+), (-), (*) :: a -> a -> a
negate :: a -> a
abs, signum :: a -> a
fromInteger :: Integer -> a
x-y = x + negate y

146 6. Abstraktion
Behandlung numerischer Literale: 5 wird interpretiert als fromInteger (5::Integer).
Beispiel für eine Instanzdeklaration:
instance Num Rat where
Rat x y + Rat x’ y’ = Rat (x*y’ + x’*y) (y*y’)
Rat x y * Rat x’ y’ = Rat (x*x’) (y*y’)
negate (Rat x y) = Rat (negate x) y
abs (Rat x y) = Rat (abs x) (abs y)
signum (Rat x y) = Rat (signum (x*y)) 1
fromInteger x = Rat (fromInteger x) 1
fromInt x = Rat (fromInt x) 1 -- Hugs-spezifisch
Eleganter: Rat parametrisiert mit einem numerischen Typ.
data (Integral a) => Rat a = Rat a a
Gibt’s vordefiniert als Ratio in der Bibliothek Rational. Gag:
instance Num Bool where
(+) = (||)
(*) = (&&)
negate = not
fromInteger n = n /= 0
fromInt n = n /= 0 -- Hugs-spezifisch
Größeres Beispiel: Zahlen mit ∞ und −∞.
data Inf n = Fin n | Inf Bool
deriving (Eq)
oo = Inf True
finite = Fin
isFinite (Fin _) = True
isFinite (Inf _) = False
instance (Ord n) => Ord (Inf n) where
Fin m

6.3. Typklassen 147
showsPrec p (Inf True) = showString "oo"
instance (Num n) => Num (Inf n) where
Fin m + Fin n = Fin (m+n)
Fin _ + Inf b = Inf b
Inf b + Fin _ = Inf b
Inf b + Inf c
| b == c = Inf b
| otherwise = error "oo - oo"
Fin m * Fin n = Fin (m*n)
Fin m * Inf b = Inf (b == (signum m == 1))
Inf b * Fin n = Inf (b == (signum n == 1))
Inf b * Inf c = Inf (b == c)
negate (Fin m) = Fin (negate m)
negate (Inf b) = Inf (not b)
abs (Fin m) = Fin (abs m)
abs (Inf b) = Inf True
signum (Fin m) = Fin (signum m)
signum (Inf False) = Fin (-1)
signum (Inf True) = Fin 1
fromInteger i = Fin (fromInteger i)
fromInt i = Fin (fromInt i) -- Hugs-spezifisch
minimum’, maximum’ :: (Ord n, Num n) => [Inf n] -> Inf n
minimum’ = foldr min oo
maximum’ = foldr max (-oo)
minimum’ [4,8,2,56,8]
Problem der Eindeutigkeit (da capo):
phyth :: (Floating a) => a -> a -> a
phyth x y = sqrt (xˆ2 + yˆ2)
Die Funktion (ˆ) hat den Typ (Num a, Integral b) => a -> b -> a, 2 hat den
Typ (Num a) => a; somit erhält xˆ2 den Typ ((Num a, Integral b) => a). Problem:
Welcher Typ soll für b gewählt werden? Int oder Integer? Da Mehrdeutigkeiten
bei numerischen Typen besonders häufig auftreten, kann das mit Hilfe einer default-
Deklaration festgelegt werden.
default (Int,Double)
Grit Garbo: FALSCH: 0 * oo ist mathematisch nicht definiert!!!

148 6. Abstraktion
6.4. Anwendung: Sequenzen
6.4.1. Klassendefinition
Binärbäume lassen sich als Sequenzen deuten: Leaf a formt eine einelementige Liste, Br
hängt zwei Listen aneinander. Vergleichen wir die Typen von (++) und Br (wir notieren
den Listenkonstruktor präfix: statt [a] einfach [] a).
(++) :: [] a -> [] a -> [] a
Br :: Tree a -> Tree a -> Tree a
Beachte: es wird über einen Typkonstruktor abstrahiert.
class Sequence s where
empty :: s a
single :: a -> s a
isEmpty, isSingle :: s a -> Bool
( s a -> s a
(|>) :: s a -> a -> s a
hd :: s a -> a
tl :: s a -> s a
() :: s a -> s a -> s a
len :: s a -> Int
fromList :: [a] -> s a
toList :: s a -> [a]
Je nachdem, ob die Klassenmethoden Sequenzen zusammensetzen, in Komponenten
zerlegen oder Eigenschaften feststellen, nennt man sie Konstruktoren, Selektoren oder
Observatoren.

6.4. Anwendung: Sequenzen 149
Die Definition subsumiert Stapel (engl. stacks): (), hd, tl. Spezifikation:
Default-Methoden:
empty = 〈〉
single a = 〈a〉
isEmpty 〈a1 . . . an〉 = n = 0
isSingle 〈a1 . . . an〉 = n = 1
a a = 〈a1 . . . ana〉
hd 〈a1 . . . an〉 = a1
tl 〈a1 . . . an〉 = 〈a2 . . . an〉
〈a1 . . . am〉 〈b1 . . . bn〉 = 〈a1 . . . amb1 . . . bn〉
len 〈a1 . . . an〉 = n
fromList [a1, . . . , an] = 〈a1 . . . an〉
toList 〈a1 . . . an〉 = [a1, . . . , an]
single a = a b -> s a -> b
foldrS (*) e s
| isEmpty s = e
| otherwise = hd s * foldrS (*) e (tl s)
Als Anwendung programmieren wir eine stabile Version von Quicksort. Ein Sortierverfahren
heißt stabil, wenn Elemente mit gleichem Schlüssel beim Sortieren ihre relative
Anordnung beibehalten. Diese Eigenschaft erlaubt sukzessives Sortieren nach verschiedenen
Kriterien.
Wir verwenden (|>) anstelle von (:).
Übung 6.10 Definiere foldlS und foldr1S.
Übung 6.11 Zeige, daß das Programm von Qsort aus Abschnitt
6.1 nicht stabil ist. Dafür gibt es sogar zwei Gründe!

150 6. Abstraktion
qsortS :: (Sequence s, Sequence t, Ord a) => s a -> t a
qsortS x
| isEmpty x = empty
| otherwise = partitionS (tl x) empty (hd x) empty
partitionS :: (Sequence s, Sequence t, Ord a) => s a -> s a -> a -> s a -> t a
partitionS x l a r
| isEmpty x = qsortS l (single a qsortS r)
| a b)
| otherwise = partitionS (tl x) (l |> b) a r
where b = hd x
Beachte: der Typ wäre nicht so allgemein, wenn wir in der ersten Gleichung von qsortS
den Ausdruck empty durch x ersetzen würden.
6.4.2. Einfache Instanzen
Allgemein gilt, daß wir die Default-Methoden nur dann ersetzen, wenn eine bessere asymptotische
Laufzeit erreicht wird.
Listen sind Sequenzen ([] ist der Typkonstruktor):
instance Sequence [] where
empty = []
isEmpty = null
(

6.4. Anwendung: Sequenzen 151
isEmpty t = False
() = Br
etc.
Allerdings scheitert diese Idee an Fällen wie isEmpty (Nil Nil) = False, die
im Widerspruch zur Spezifikation stehen. Das Problem liegt darin, daß der Datentyp Tree
unterschiedliche Repräsentationen der gleiche Sequenz erlaubt. Grundsätzlich gibt es zwei
Wege, dieses Problem zu lösen: Man kann die Sequenz-Konstruktoren so definieren, daß
sie keine „unerwünschten“ Repräsentationen (wie oben Br Nil Bil statt einfach Nil)
erzeugen. Oder man programmiert die Observatoren und Selektoren so, daß sie mit allen
möglichen Repräsentationen korrekt umgehen.
Zu Demonstrationszwecken wenden wir hier beide Techniken an.
instance Sequence Tree where
empty = Nil
isEmpty Nil = True
isEmpty (Leaf _) = False
isEmpty (Br l r) = isEmpty l && isEmpty r
single = Leaf
isSingle Nil = False
isSingle (Leaf _) = True
isSingle (Br l r) = isSingle l /= isSingle r
hd (Leaf a) = a
hd (Br l r)
| isEmpty l = hd r
| otherwise = hd l
tl (Br Nil r) = tl r
tl (Br (Leaf _) r) = r
tl (Br (Br l’ r’) r) = tl (Br l’ (Br r’ r)) -- Rechtsrotation
() = br where -- smart Konstruktor
br Nil r = r
br l Nil = l
br l r = Br l r
toList = leaves
fromList [] = Nil
fromList [a] = Leaf a
fromList (a:as) = a

Übung 6.14 Sequenzen über beliebigen Alphabeten lassen sich
nach einer Technik von Gödel als Zahlen codieren. Hier am Beispiel
über dem Alphabet der positiven ganzen Zahlen:
data GoedelNr = G Integer deriving Show
goedelize :: [Integer] -> GoedelNr
goedelize ns = G (g primes ns)
where g ps [] = 1
g (p:ps) (n:ns) = pˆn * g ps ns
Führe diese Technik für beliebige Alphabete a durch und mache
den Typ GoedelNr a zur Instanz von Sequence.
Übung 6.15 Listen mit Löchern als (nicht-generische) Instanz.
Vorübung zur nächsten Aufgabe.
data LList a = LL ([a] -> [a])
abra, kad :: LList Char
abra = LL ("abra"++) -- Beispieldaten
kad = LL ("kad"++)
abrakadabra = toList (abra (kad abra))
Erkläre LList zur Instanz von Sequence.
Übung 6.16 Sequenzen mit Löchern als generische Instanz.
data Iso s a = Iso (s a -> s a)
152 6. Abstraktion
Schlechtes Verhalten bei:
6.4.3. Generische Instanzen
t0 = empty . . . , ti+1 = ti |> ai, hd ti+1 . . .
Erweiterung eines Sequenzenkonstruktors, so daß die Länge in konstanter Zeit berechnet
wird. WithLen hat Kind von (* -> *) -> (* -> *).
data WithLen s a = Len (s a) Int
Beachte: deriving (Show) geht nicht, da die Voraussetzung Show (s a) nicht zulässig
ist.
instance (Sequence s) => Sequence (WithLen s) where
empty = Len empty 0
single a = Len (single a) 1
isEmpty (Len _ n) = n == 0
isSingle (Len _ n) = n == 1
a a) (n+1)
hd (Len s _) = hd s
tl (Len s n) = Len (tl s) (n-1)
Len s m Len t n = Len (s t) (m+n)
len (Len _ n) = n
fromList x = Len (fromList x) (length x)
toList (Len s _) = toList s
Ein angenehmer Seiteneffekt: Auch isEmpty und isSingle laufen in konstanter Zeit.
Anwendung:
type List = WithLen []
Durch diese Defintion erhalten wir einen Listentyp, der sozusagen die Länge der Listen
„cached“ und effizienten Zugriff gestattet.
6.4.4. Schlangen
Ziel: (|>), hd und tl in konstanter Zeit. Das sind die typischen Operationen für Schlangen
(engl. queues). Ausgangspunkt: (

6.4. Anwendung: Sequenzen 153
data FrontRear s t a = FrontRear (s a) (t a)
Wir tragen Sorge, daß die erste Liste immer mindestens ein Element enthält. Invariante
für FrontRear f r:
isEmpty f =⇒ isEmpty r (6.1)
instance (Sequence s, Sequence t) => Sequence (FrontRear s t) where
empty = FrontRear empty empty
isEmpty (FrontRear f r) = isEmpty f
FrontRear f r |> a = frontRear f (a s a -> t a -> FrontRear s t a
frontRear f r
| isEmpty f = FrontRear (rev r) empty
| otherwise = FrontRear f r
Amortisierte Analyse: gutartig für (Queue wird ephemeral verwendet):
q0, hd q0, q1 = tl q0, . . . , hd qn−1, qn = tl qn−1
Schlechtes Verhalten bei (Queue wird persistent verwendet):
q = FrontRear [a] r, qi = tl (q |> ai), hd qi
Idee: das Umdrehen muß frühzeitig erfolgen. Einführung einer Balanzierungsbedingung.
Invariante für FrontRear f r:
len f len r (6.2)
Beachte: (6.1) impliziert (6.2). Voraussetzung: erfolgt inkrementell. Und: len in konstanter
Zeit.
frontRear :: (Sequence s, Sequence t) => s a -> t a -> FrontRear s t a
frontRear f r
| len f < len r = FrontRear (f rev r) empty
| otherwise = FrontRear f r

154 6. Abstraktion
Amortisierte Laufzeit von Θ(1). Worst case Laufzeit von Θ(n). Anwendung:
type Queue = FrontRear List List
6.4.5. Konkatenierbare Listen
Ziel: hd, tl und () in konstanter Zeit. Binärbäume bieten schon () in konstanter
Zeit. Left-spine view:
data GTree s a = GNode a (s (GTree s a))
instance (Sequence s) => Sequence (GTree s) where
single a = GNode a empty
isSingle (GNode _ s) = isEmpty s
hd (GNode a _) = a
tl (GNode _ s)
| isEmpty s = error "tl of singleton"
| otherwise = foldr1S () s
GNode a s g = GNode a (s |> g)
Anwendung:
type CatList = AddEmpty (GTree Queue)

A. Lösungen aller Übungsaufgaben
3.1 Hier ist die Definition von not:
not :: Bool -> Bool -- vordefiniert
not True = False
not False = True
Die Definitionen von (&&) und (||) bedienen sich im wesentlichen der entsprechenden
Wertetabelle für die Konjunktion bzw. für die Disjunktion. Gleiche Fälle werden zusammengefaßt.
(&&), (||) :: Bool -> Bool -> Bool -- vordefiniert
False && y = False
True && y = y
True || y = True
False || y = y
[(&&) und (||) sind lazy!]
3.2 Definition von first, second und third:
first :: (a, b, c) -> a
first (a, b, c) = a
second :: (a, b, c) -> b
second (a, b, c) = b
third :: (a, b, c) -> c
third (a, b, c) = c
3.3 Definition von head’’:
head’’ :: List a -> a
head’’ Empty = error "head’’ of empty list"
head’’ (Single a) = a
head’’ (App Empty r) = head’’ r
head’’ (App (Single a) r) = a
head’’ (App (App ll lr) r) = head’’ (App ll (App lr r))

156 A. Lösungen aller Übungsaufgaben
Wenn man vereinbart, daß Empty nie unterhalb von App auftritt, dann ist die Definition
einfacher.
tail’ :: List a -> List a
tail’ Empty = error "tail’ of empty list"
tail’ (Single a) = Empty
tail’ (App Empty r) = tail’ r
tail’ (App (Single a) r) = r
tail’ (App (App ll lr) r) = tail’ (App ll (App lr r))
3.4 Definition von member:
member’ :: (Ord a) => a -> OrdList a -> Bool
member’ a [] = False
member’ a (b:bs) = a >= b && (a == b || member’ a bs)
Beachte: die Klammern sind notwendig, da (&&) stärker bindet als (||).
3.5 Man sollte Grit zunächst klarmachen, daß links- und rechtsassoziativ rein syntaktische
Eigenschaften sind, die dem Haskell-Übersetzer mitteilen, wie fehlende Klammern
zu ergänzen sind. Mathematisch gesehen ist die Listenkonkatenation assoziativ: Wie man
x1++x2++x3 auch klammert, der Wert des Ausdrucks ist stets der gleiche. Warum vereinbart
man (++) dann als rechtsassoziativ? Nun, das hat Effizienzgründe: Sei ni die Länge
der Liste xi; um (x1++x2)++x3 auszurechnen, benötigt man 2n1 + n2 Anwendungen von
„:“, für x1++(x2++x3) hingegen nur n1 + n2. Die arithmetischen Operatoren werden aus
Gründen der Einheitlichkeit als linksassoziativ deklariert: die Operatoren (-) und (/)
sind es auch und dies aus gutem Grund, wie wir gesehen haben.
3.6 Funktionen auf Cartesischen Produkten sind die bessere Wahl, wenn das Paar oder
das n-Tupel semantisch zusammengehört; etwa wenn ein Paar eine Koordinate in der
Ebene repräsentiert.
3.7 Die Ausdrücke bezeichnen die folgenden Bäume:
1. Br (Br (Leaf 1) (Leaf 2)) Nil
2. Br (Br (Leaf 1) (Leaf 2))
(Br (Br (Leaf 3) Nil)
(Br (Leaf 4) (Leaf 5)))
3. Br (Br (Br (Leaf 1) (Leaf 2))
(Br (Leaf 3)
(Br (Leaf 4)
(Br (Leaf 5) (Leaf 6)))))
(Br (Leaf 7) (Leaf 8))

3.8 Die Ausdrücke bezeichnen die folgenden Bäume:
ɛ
1 2 1 2 ɛ 3
4 5
1 2
3 4
(1) (2) (3)
5
6 7 8
Diese Bäume erhält man übrigens durch Spiegelung der Bäume aus Aufgabe 3.7 (die Blätter
müssen zusätzlich neu durchnumeriert werden).
3.9 Definition von leaves’ mit case-Ausdrücken:
leaves’’ :: Tree a -> [a]
leaves’’ t = case t of
Nil -> []
Leaf a -> [a]
Br l r -> case l of
Nil -> leaves’’ r
Leaf a -> a : leaves’’ r
Br l’ r’ -> leaves’’ (Br l’ (Br r’ r))
3.10 Definition von drop:
drop :: Int -> [a] -> [a]
drop n (a:as) | n > 0 = drop (n-1) as -- vordefiniert
drop _ as = as
3.11 Rechenregeln für if:
if True then e1 else e2 ⇒ e1
if False then e1 else e2 ⇒ e2
Schreibt man die Rechenregeln als Programm, erhält man eine Boole’sche Funktion
ifThenElse.
ifThenElse’ :: Bool -> a -> a -> a
ifThenElse’ True a a’ = a
ifThenElse’ False a a’ = a’
3.12 Es ist ungeschickt, zunächst alle Parameter von take auszurechnen, da die Auswertung
von x nicht terminiert.
157

158 A. Lösungen aller Übungsaufgaben
4.1 [Didaktische Anmerkung: (a) übt Vorbedingungen ein, (b) den Umgang mit Quantoren.]
(a) Die Vorbedingung an die Argumente von merge drücken wir mittels einer
Implikation aus:
ordered x = True ∧ ordered y = True =⇒ ordered (merge x y) = True (A.1)
bag (merge x y) = bag x ⊎ bag y (A.2)
(b) Im Fall von mergeMany müssen wir „alle Elemente der Eingabeliste“ formalisieren.
member :: (Eq a) => a -> [a] -> Bool
member a [] = False
member a (b:x) = a == b || member a x
Mit a ∈ x kürzen wir member a x = True ab.
((∀a ∈ x) ordered a = True) =⇒ ordered (mergeMany x) = True (A.3)
] bag a | a ∈ x = bag (mergeMany x) (A.4)
[ und . . . | . . . erklären.]
4.2 Zusätzlich kann man fordern: Die Längen der Teillisten nehmen zu und die Länge
zweier benachbarter Teillisten unterscheidet sich höchstens um 1.
upstairs :: [Int] -> Bool
upstairs [] = True
upstairs [n] = True
upstairs (n1:n2:ns) = up n1 n2 && upstairs (n2:ns)
where up n1 n2 = n1 == n2 || n1+1 == n2
Sei xs = split n x, dann muß zusätzlich upstairs (map length xs) gelten.
Eine Liste der Länge l läßt sich damit in n − l mod n Listen der Länge ⌊l/n⌋ und in
l mod n Listen der Länge ⌈l/n⌉ zerlegen.
split :: Int -> [a] -> [[a]]
split n as = repeatedSplit ns as
where (d,r) = divMod (length as) n
ns = replicate (n-r) d ++ replicate r (d+1)
Die vordefinierte Funktion divMod faßt div und mod zusammen.
repeatedSplit :: [Int] -> [a] -> [[a]]
repeatedSplit [] as = []
repeatedSplit (n:ns) as = x : repeatedSplit ns as’
where (x, as’) = splitAt n as

Die vordefinierte Funktion splitAt faßt take und drop zusammen. In [GKP94] wird
das folgende Verfahren vorgeschlagen:
split’ n as = splitn (length as) n as
splitn l 1 as = [as]
splitn l n as = x : splitn (l-k) (n-1) as’
where k = l ‘div‘ n
(x, as’) = splitAt k as
Daß die Funktion das gleiche leistet, ist nicht unmittelbar einsichtig; die interessierte
Leserin sei für den Nachweis auf [GKP94] verwiesen.
4.3 Definition von branches:
branches :: Tree a -> Integer
branches Nil = 0
branches (Leaf a) = 0
branches (Br l r) = 1 + branches l + branches r
159
4.4 Die erste Definition von leaves in Abschnitt 3.4 ist strukturell rekursiv; die zweite
ist es nicht, da der rekursive Aufruf leaves (Br l’ (Br r’ r)) nicht über eine
Teilstruktur des Arguments erfolgt.
4.5 Die folgenden Funktionen aus Kapitel 2 sind strukturell rekursiv definiert:
transponiere, wc_complement, complSingleStrand, exonuclease, genCode,
ribosome, triplets, translate, findStartPositions.
Dito für Kapitel 3:
ifThenElse, fst, snd, (++), head, tail, reverse, minimum1, map, minimum,
length, dropSpaces, squeeze, member, splitWord, minimum0’, leaves,
leftist, take.
4.6 Wir definieren zunächst eine Hilfsfunktion leavesTo mit der folgenden Eigenschaft.
leavesTo :: Tree a -> [a] -> [a]
leavesTo t y = leaves t ++ y
Analog zur Vorgehensweise bei reverse läßt sich die folgende Definition von leavesTo
ableiten.
leavesTo :: Tree a -> [a] -> [a]
leavesTo Nil y = y
leavesTo (Leaf a) y = a:y
leavesTo (Br l r) y = leavesTo l (leavesTo r y)

160 A. Lösungen aller Übungsaufgaben
Die Funktion leaves ergibt sich wiederum durch durch Spezialisierung von leavesTo.
leaves’ :: Tree a -> [a]
leaves’ t = leavesTo t []
4.7 Die Begründung ist hier nicht stichhaltig — erstens weil unendliche Listen nicht in
einem [] enden, zweitens weil der Beweis bei der elementweisen Konstruktion nie fertig
werden würde.
4.10 Die Funktion complete n konstruiert einen vollständigen Baum der Tiefe n.
complete :: Integer -> Tree a
complete 0 = Nil
complete (n+1) = Br t t
where t = complete n
4.11 Nachweis von Aussage 4.14. Induktionsbasis (t = Nil):
branches Nil + 1
= 1 (Def. branches)
= size Nil (Def. size)
Induktionsbasis (t = Leaf a): analog. Induktionsschritt (t = Br l r):
branches (Br l r) + 1
= (branches l + branches r + 1) + 1 (Def. branches)
= size l + size r (I.V.)
= size (Br l r) (Def. size)
4.13 Die Multiplikation auf Natural:
mutlN :: Natural -> Natural -> Natural
mutlN Zero n = Zero
mutlN (Succ m) n = addN (mutlN m n) n
Möchte man — wie Harry — die üblichen Symbole zum Rechnen verwenden, muß man
Natural zu einer Instanz der Typklasse Num machen.
instance Num Natural where
(+) = addN
Zero - n = Zero
Succ m - Zero = Succ m
Succ m - Succ n = m-n
(*) = mutlN
fromInteger 0 = Zero
fromInteger (n+1) = Succ (fromInteger n)

Mehr dazu in Abschnitt 6.3.
4.14 Eine erste (naive) Definition könnte so aussehen:
naiveBraun :: Tree a -> Bool
naiveBraun Nil = True
naiveBraun (Leaf a) = True
naiveBraun (Br l r) = size l += size r && naiveBraun l && naiveBraun r
(+=) :: (Num a) => a -> a -> Bool
m += n = m == n || m+1 == n
Diese Definition krankt daran, daß für jeden Teilbaum erneut die Größe ausgerechnet
wird. Durch Rekursionsverstärkung läßt sich dieses Manko beheben.
braun :: Tree a -> Bool
braun t = fst (check t)
where
check :: Tree a -> (Bool, Integer)
check Nil = (True, 1)
check (Leaf a) = (True, 1)
check (Br l r) = (sl += sr && bl && br, sl + sr)
where (bl, sl) = check l
(br, sr) = check r
161
Die Hilfsfunktion check bestimmt zwei Dinge gleichzeitig: die Braun-Eigenschaft und
die Größe des Baums.
4.17 Die Braun-Eigenschaft legt einen Baum in seiner Struktur fest, nicht aber in der
Beschriftung der Blätter. Deshalb ist die Spezifikation nicht eindeutig. Um 4.27 nachzuweisen,
zeigt man zuerst
size (extend a t) = size t + 1 . (A.5)
4.20 Die Fälle t = Nil und t = Leaf a folgen direkt aus den Definitionen. Fall t =
Br Nil \(r\): Da weight t = 1 + weight \(r\) ist die Induktionsvorausetzung auf
r anwendbar.
=
bag (leaves (Br (Leaf a) r))
bag (a:leaves r) (Def. leaves)
= a ⊎ bag (leaves r) (Def. bag)
= a ⊎ bag r (I.V.)
= bag (Leaf a) ⊎ bag r (Def. bag)
= bag (Br (Leaf a) r) (Def. bag)

162 A. Lösungen aller Übungsaufgaben
Fall t = Br (Leaf a) r: analog. Fall t = Br (Br l’ r’) r: Wir haben bereits nachgerechnet,
daß die Induktionsvorausetzung auf Br l’ (Br r’ r) anwendbar ist.
5.1
bag (leaves (Br (Br l’ r’) r))
= bag (leaves (Br l’ (Br r’ r))) (Def. leaves)
= bag (Br l’ (Br r’ r)) (I.V.)
= bag l’ ⊎ (bag r’ ⊎ bag r) (Def. bag)
= (bag l’ ⊎ bag r’) ⊎ bag r (Ass. (⊎))
= bag (Br (Br l’ r’) r)) (Def. bag)
insert = \a -> \x -> case x of {
[] -> a:[];
b:y -> case a a:(b:x);
False -> b:((insert a) y)}}
5.2 Der Unterschied liegt nur im konstanten Faktor.
5.6 Da weder length noch take noch drop Vergleichsoperationen verwenden, ergeben
sich folgende Rekurrenzgleichungen für mergeSort:
T mergeSort (0) = 0
T mergeSort (1) = 0
T mergeSort (n) = n − 1 + T mergeSort (⌊n/2⌋) + T mergeSort (⌈n/2⌉) für n > 1
Diese Form der Rekurrenzgleichung ist typisch für Programme, die auf dem „Teile und
Herrsche“-Prinzip basieren. Rechnen wir die Kostenfunktion zunächst einmal für den Fall
aus, daß die Halbierung stets aufgeht:
T mergeSort (2 m ) = 2 m − 1 + 2T mergeSort(2 m−1 )
Einer ähnlichen Rekurrenz sind wir schon im letzten Abschnitt begegnet:
T mergeSort (2 m ) = T ′
sT(m) = m2 m − 2 m + 1

Die obige Formel läßt sich gut mit Hilfe des Rekursionsbaums von mergeSort illustrieren
(für m = 4):
1*(16-1) o o 1*(16-1)-3
/ \ / \
2*( 8-1) o o o o 2*( 8-1)-3
/ \ / \ / \ / \
4*( 4-1) o o o o o o o o 4*( 4-1)-3
/\ /\ /\ /\ /\ /\ /\ /\
8*( 2-1) o o o o o o o o o o o o o o o o 8*( 2-1)-3
/\/\/\/\/\/\/\/\ \/\ \/\ \/\/\/\
163
Wenn die Länge der zu sortierenden Liste keine Potenz von 2 ist, erhalten wir einen Baum
dessen unterste Ebene ausgefranst ist: Sei m = ⌈log 2 n⌉, dann fehlen 2 m −n Elemente. Um
diese Anzahl verringern sich gerade die Kosten pro Ebene. Da es m Ebenen gibt, erhalten
wir:
6.10
T mergeSort(n) = T mergeSort(2 m ) − m(2 m − n) = mn − 2 m + 1 mit m = ⌈log 2 n⌉
T mergeSort (n) ∈ Θ(n log n).
foldlS :: (Sequence s) => (a -> b -> a) -> a -> s b -> a
foldlS (*) e = f e
where f e s | isEmpty s = e
| otherwise = f (e * hd s) (tl s)
foldr1S :: (Sequence s) => (a -> a -> a) -> s a -> a
foldr1S (*) s
| isSingle s = hd s
| otherwise = hd s * foldr1S (*) (tl s)
Beispiele:
rev :: (Sequence s, Sequence t) => s a -> t a
rev = foldlS (flip (

164 A. Lösungen aller Übungsaufgaben
6.12 Im ersten Fall muss man dafür sorgen, daß zur Konstruktion von Sequenzen nur die
Konstruktoren der Klasse, aber nicht unmittelbar die des Datentyps verwendet werden.
Im zweiten Fall können sehr ineffiziente Repräsentationen entstehen.
6.14 – Nur Vorüberlegungen zum Spezialfall!
split :: GoedelNr -> (Integer,GoedelNr)
split (G m) = splt primes 0 m
where
splt (p:ps) e m
| m ‘mod‘ p == 0 = splt (p:ps) (e+1) (m ‘div‘ p)
| e == 0 = splt ps 0 m
| otherwise = (e, G m)
Achtung: bei split (G m) = (u,G v) ist (G v) NICHT die GoedelNr. der verkürzten
Liste.
degoedelize :: GoedelNr -> [Integer]
degoedelize (G m) | m == 1 = []
| otherwise = n:degoedelize ns
where (n,ns) = split (G m)
instance (Integral a) => Sequence (GoedelNr a )
where empty = G 1
isEmpty (G m) = (m == 1)
hd (G m) = n
where (n,ns) = split (G m)
tl (G m) = ns
where (n,ns) = split (G m)
(G m) |> n = let k = len (G m)
in G (m* (primes !! (k+1))ˆn)
(G m) (G n) | isEmpty (G n) = (G m)
| otherwise = ((G m) |> a) (G as)
where (a:as) = split n
fromList = goedelize
toList = degoedelize

6.15
instance Sequence LList where
empty = LL id
isEmpty (LL s) = isEmpty (s [])
single a = LL (a:)
isSingle (LL s) = isSingle (s [])
(LL s) (LL t) = LL (s . t)
hd (LL s) = head (s [])
tl (LL s) = LL h where
h r = tail (s r)
len (LL s) = len (s [])
165

166 A. Lösungen aller Übungsaufgaben

B. Mathematische Grundlagen
oder: Wieviel Mathematik ist nötig?
B.1. Mengen und Funktionen
B.1.1. Der Begriff der Menge
Eine Menge ist eine abstrakte Zusammenfassung unterschiedener Objekte. Wir schreiben
x ∈ M, wenn x ein Element von M ist, und x /∈ M, wenn x kein Element von M ist.
In der Schule haben wir es häufig mit Mengen von Zahlen zu tun. Wir verwenden N
für die Menge der natürlichen Zahlen 1 , Z für die Menge der ganzen Zahlen und R für die
Menge der reellen Zahlen.
Mengen werden z.B. durch Aufzählung definiert.
N37 := {3, 4, 5, 6, 7}
HS := {Harry, Sally}
M1 := {M, A, T, H, E, I, K} (Buchstaben des Wortes MATHEMATIK)
Bool := {False, True} (Menge der „Wahrheitswerte“)
Abstrakt ist die Menge als Zusammenfassung ihrer Elemente in dreifacher Hinsicht:
1. die Elemente stehen in keiner besonderen Anordnung, z.B. {M, A, T, H, E, I, K} =
{A, E, I, H, K, T, M},
2. die Elemente gehören der Menge nicht mit unterschiedlicher Intensität oder Häufigkeit
an, z.B. {M, A, T, H, E, I, K} = {M, A, T, H, E, M, A, T, I, K},
3. es wird nicht verlangt, daß die zusammengefaßten Elemente überhaupt in irgendeinem
logischen Zusammenhang stehen.
Der letzte Punkt bedeutet, daß mathematisch gegen die Definition der Menge
Allerlei := {Lisa Listig’s PC, die Oper „Don Giovanni“,
der Lombardsatz der Deutschen Bundesbank}
1 Im Unterschied zum Gebrauch in der Mathematik zählt die Informatik die 0 zu den natürlichen Zahlen.

168 B. Mathematische Grundlagenoder: Wieviel Mathematik ist nötig?
nichts einzuwenden ist, obwohl man sich schwerlich einen Zusammenhang vorstellen
kann, indem diese Menge kein Unfug ist. Diese Gleichgültigkeit in bezug darauf, welche
Art von Objekten man in eine Menge faßt, darf man allerdings nicht ungestraft auf die
Spitze treiben. Als Russell’sche Antinomie berühmt ist die Menge aller Mengen, die sich
selbst nicht enthalten. Solche Gefahren werden für uns keine Rolle spielen und wir gehen
nicht weiter auf sie ein.
Mengen werden oft durch Angabe einer charakterisierenden Eigenschaft definiert.
Prim := { x | x ∈ N und x ist Primzahl }
N37 := { x | x ∈ N und 3 x 7 }
NullSt := { x | x 5 − x 3 = 8x 2 − 9 = 0 }
N := { x | x = 0 oder (x = y + 1 und y ∈ N) }
Eine Definition durch eine charakteristische Eigenschaft unterstellt eine umfassendere
Menge, deren Elemente auf diese Eigenschaft hin zu prüfen sind. Bei Prim und N37 ist
diese Menge N. Die Definition von NullSt ist gerade deswegen anfechtbar, weil die Bezugsmenge
nicht genannt wird. Sind ganze, reelle oder komplexe Nullstellen gemeint? Die
hier gegebene Definition von N dagegen bezieht sich auf sich selbst und setzt dabei das
Bildungsgesetz der natürlichen Zahlen — das Zählen — voraus. Solche Definitionen nennt
man rekursiv. Das Zählen ist nichts als der Übergang von einer natürlichen Zahl zur nächsten.
Wir haben es hier durch die Operation +1 bezeichnet, so daß unsere natürlichen
Zahlen nach dieser Definition statt des vertrauten 0, 1, 2 . . . das ungewöhnliche Aussehen
0, 0 + 1, (0 + 1) + 1 usw. haben.
Eine Menge M ist Teilmenge von N (M ⊆ N), wenn jedes Element von M auch Element
von N ist.
M ⊆ N ⇐⇒ (∀a) a ∈ M ⇒ a ∈ N
Die Vereinigung von M und N (M ∪ N) ist definiert durch
M ∪ N = { a | a ∈ M oder a ∈ N }
Dabei ist das „oder“ nicht ausschließend zu verstehen. Der Durchschnitt von M und N
(M ∩ N) ist definiert durch
M ∩ N = { a | a ∈ M und a ∈ N }.
Mit den gegebenen Definitionen läßt sich z.B. zeigen, daß ∪ und ∩ assoziative Operationen
sind:
K ∪ (M ∪ N) = (K ∪ M) ∪ N
K ∩ (M ∩ N) = (K ∩ M) ∩ N

B.2. Relationen und Halbordnungen 169
Die Potenzmenge einer Menge M ist die Menge aller Teilmengen von M:
P(M) = { T | T ⊆ M }
Da für alle Mengen M stets ∅ ⊆ M und M ⊆ M gilt, enthält P(M) stets ∅ und M. Das
Cartesische Produkt zweier Mengen M und N ist die Menge aller möglichen Elementpaare:
M × N = { (x, y) | x ∈ M und y ∈ N }
Das Cartesische Produkt verallgemeinert man auf n 2 Mengen und spricht dann von
n-Tupeln.
B.1.2. Der Begriff der Funktion
Seien A, B Mengen. Eine partielle Funktion f von A nach B hat den Vorbereich A, den
Nachbereich B und ordnet gewissen Elementen aus A (den Argumenten) jeweils ein Element
aus B zu (den Wert). Man schreibt f : A → B und f(a) = b oder f : a ↦→ b. Sind
A und B Mengen, so bezeichnet A → B die Menge der partiellen Funktionen mit Vorbereich
A und Nachbereich B. Ist die Menge A ein kartesisches Produkt A = (A1, . . . , An),
so nennt man f auch n-stellige Funktion.
Die Menge
Def (f) := { a ∈ A | es gibt b ∈ B mit f(a) = b }
heißt Definitionsbereich von f, die Menge
Im(f) := { b ∈ B | es gibt a ∈ A mit f(a) = b }
heißt Bildbereich von f. Ist Def (f) = A, heißt f totale Funktion.
Bekannte Beispiele von Funktionen sind die Grundrechnungsarten, Polynome, trigonometrische
Funktionen usw. über R. Davon sind z.B. Division und Tangens partielle Funktionen,
da Divisor 0 bzw. π
2 nicht zum Definitionsbereich gehören. Das Differenzieren
kann man selbst als Funktion (·) ′ ansehen:
(·) ′
: (R → R) → (R → R).
B.2. Relationen und Halbordnungen
Eine Funktion ordnet gewissen Elementen des Vorbereichs ein Element des Nachbereichs
zu. Relationen geben im Unterschied dazu beliebige Beziehungen zwischen zwei Mengen

170 B. Mathematische Grundlagenoder: Wieviel Mathematik ist nötig?
an: Einem Element des Vorbereichs können durchaus mehrere Elemente des Nachbereichs
zugeordnet werden. Formal ist eine zweistellige Relation eine Teilmenge R ⊆ M × N. Statt
(a, b) ∈ R schreibt man auch oft aRb.
Eine Relation R ⊆ M × M heißt Halbordnung auf M, wenn R
1. reflexiv, (∀x ∈ M) xRx,
2. antisymmetrisch, (∀x, y ∈ M) (xRy und yRx) ⇒ x = y, und
3. transitiv, (∀x, y, z ∈ M) (xRy und yRz) ⇒ xRz, ist.
Ein Beispiel für eine Halbordnung ist etwa die Teilmengenbeziehung (⊆). Das Wörtchen
„Halb“ deutet an, daß es in der Regel Elemente gibt, die nicht miteinander vergleichbar
sind: Die Mengen {1, 2} und {2, 3} sind z.B. unvergleichbar. Ist jedes Element mit jedem
vergleichbar, spricht man von einer totalen Ordnung.
B.3. Formale Logik
B.3.1. Aussagenlogik
Um Sachverhalte, Eigenschaften etc. präzise aufschreiben zu können, verwendet man aussagenlogische
bzw. prädikatenlogische Formeln. Wir haben selbst schon einige Formeln
verwendet, um z.B. die Mengeninklusion (⊆) oder Eigenschaften von Relationen (Transitivität)
zu notieren.
In der klassischen Logik ist eine Formel entweder wahr oder falsch. Für die Menge
dieser Wahrheitswerte sind verschiedene Schreibweisen gebräuchlich:
Bool = {False, True} (in der Programmierung)
= {0, 1} (im Hardware-Entwurf)
= {F, W } (in der formalen Logik).
Die wichtigsten Boole’schen Funktionen sind „und“ (∧), „oder“ (∨) und „nicht“ (¬), definiert
durch die folgende Wertetabelle:
a b a ∧ b a ∨ b ¬a
False False False False True
False True False True True
True False False True False
True True True True False

B.3. Formale Logik 171
Eine Formel ist aus False, True, ∧, ∨, ¬ und Variablen zusammengesetzt. Wir können
„und“, „oder“ und „nicht“ auch durch Gleichungen definieren:
False ∧ x = False
True ∧ x = x
False ∨ x = x
True ∨ x = True
¬False = True
¬True = False
Durch eine vollständige Fallunterscheidung über das erste Argument sind ∧, ∨ und ¬
totale Funktionen. Mit Hilfe dieser Definitionen zeigt man wichtige Eigenschaften: Für
alle a, b, c ∈ Bool gilt z.B.:
a ∧ a = a (Idempotenz)
(a ∧ b) ∧ c = a ∧ (b ∧ c) (Assoziativität)
a ∧ b = b ∧ a (Kommutativität)
a ∧ (a ∨ b) = a (Absorption)
a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) (Distributivität)
¬¬a = a (doppelte Negation)
Interessanterweise gelten die Gleichungen auch, wenn man konsistent ∧ durch ∨ und ∨
durch ∧ ersetzt. Wir beweisen das Absorptionsgesetz: Fall a = False:
False ∧ (False ∨ b) = False (Definition von ∧)
Fall a = True:
True ∧ (True ∨ b) = True ∨ b (Definition von ∧)
= True (Definition von ∨)
In Formeln verwendet man oft noch weitere Boole’schen Funktionen wie ⇒ (Implikation)
und ⇐⇒ (Äquivalenz), die sich einfach auf die bisher bekannten zurückführen lassen.
a ⇒ b = ¬a ∨ b
a ⇐⇒ b = (a ⇒ b) ∧ (b ⇒ a)
Zur Übung: Wie sehen die Wahrheitstafeln von ⇒ und ⇐⇒ aus? Beachte: ⇐⇒
formalisiert die Gleichheit Boole’scher Werte.
B.3.2. Prädikatenlogik
Formeln sind natürlich nicht nur aus False, True, ∧ etc. zusammengesetzt. Interessant wird
es erst, wenn man auch Aussagen über Individuen machen kann, wie z.B. in x ∈ M ⇒
x ∈ N. Hier ist x eine Individuenvariable, ein Platzhalter für Individuen. Häufig macht
man Aussagen, daß es mindestens ein Individuum mit einer bestimmten Eigenschaft gibt,

172 B. Mathematische Grundlagenoder: Wieviel Mathematik ist nötig?
oder daß eine Aussage für alle Individuen gilt. Zu diesem Zweck verwendet man den
Existenzquantor (∃) und den Allquantor (∀).
(∃x) Φ(x)
(∀x) Φ(x)
Hier ist Φ(X) irgendeine Aussage über x, z.B. Φ(x) = x ∈ M ⇒ x ∈ N. Gebräuchlich sind
auch Quantoren, bei denen der Individuenbereich direkt angegeben wird:
(∃x ∈ M) Φ(x) ⇐⇒ (∃x) x ∈ M ∧ Φ(x)
(∀x ∈ M) Φ(x) ⇐⇒ (∀x) x ∈ M ⇒ Φ(x)
B.3.3. Natürliche und vollständige Induktion
Nehmen wir an, Φ(n) ist eine Eigenschaft, die wir für alle natürlichen Zahlen n nachweisen
wollen. Dazu kann man das Prinzip der natürlichen Induktion 2 verwenden:
Induktionsbasis: Wir zeigen Φ(0).
Induktionsschritt: Wir nehmen an, daß Φ(n) gilt (Induktionsvoraussetzung) und zeigen
unter dieser Annahme, daß auch Φ(n + 1) gilt.
Diese Beweisregel kann man formal wie folgt darstellen:
Φ(0) (∀n ∈ N) Φ(n) ⇒ Φ(n + 1)
(∀n ∈ N) Φ(n)
Über dem Strich werden die Voraussetzungen aufgeführt, unter dem Strich steht die
Schlußfolgerung, die man daraus ziehen kann. Die Beweisregel kann man auch als Arbeitsprogramm
lesen (von unten nach oben): Um · · · zu zeigen, muß man · · · zeigen.
Warum leistet die natürliche Induktion das Gewünschte? Oder: Warum ist die natürliche
Induktion korrekt. Klar, es gilt Φ(0), mit dem Induktionsschritt erhalten wir Φ(1), durch
erneute Anwendung Φ(2) etc. Auf diese Weise erhalten wir Φ(n) für jede natürliche Zahl.
Wir demonstrieren das Induktionsprinzip an einem einfachen Beispiel:
Φ(n) ⇐⇒
nX
2 i = 2 n+1 − 1
i=0
2 Andere Bücher, andere Begriffe: „Natürliche Induktion“ wird auch „mathematische Induktion“ genannt. Dieser
Begriff sagt allerdings wenig aus: Sind andere Induktionsprinzipien etwa unmathematisch? Leider ist auch der
Name „vollständige Induktion“ gebräuchlich. Leider deshalb, weil wir ihn für ein anderes Induktionsprinzip
reservieren.

B.3. Formale Logik 173
Induktionsbasis: Die Rechnung ist einfach 0 i=0 2i = 1 = 21 − 1. Induktionsschritt:
n+1 X
2 i = 2 n+1 nX
+ 2 i
(Arithmetik)
i=0
i=0
= 2 n+1 + 2 n+1 − 1 (Induktionsvoraussetzung)
= 2 n+2 − 1 (Arithmetik)
Bei der natürlichen Induktion stützt man sich beim Induktionsschritt auf die Voraussetzung
ab, daß die Aussage für den unmittelbaren Vorgänger gilt. Wir können großzügiger
sein und verwenden, daß die Aussage für alle kleineren Zahlen gilt. Dies formalisiert das
Prinzip der vollständigen Induktion.
(∀m) ((∀m ′ < m) Φ(m ′ )) ⇒ Φ(m)
(∀n) Φ(n)
Zur Übung: Sind beide Induktionsprinzipien gleich mächtig?

174 B. Mathematische Grundlagenoder: Wieviel Mathematik ist nötig?

Literaturverzeichnis
[GKP94] Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete mathematics.
Addison-Wesley Publishing Company, Reading, Massachusetts, second edition
edition, 1994.